If your observed Z or t statistic falls in the "critical region," what can you conclude?
Answers
If your observed Z or t statistic falls in the "critical region," it means that the probability of obtaining a value as extreme or more extreme than the observed statistic is very low, assuming the null hypothesis is true.
The critical region is a range of values of a test statistic, such as Z or t, that indicate the rejection of the null hypothesis. In hypothesis testing, the null hypothesis is a statement that there is no significant difference between two groups or that there is no effect of an intervention. The alternative hypothesis is the opposite of the null hypothesis, and it suggests that there is a significant difference or an effect of the intervention.
The critical region is determined by the level of significance, which is a pre-specified threshold that is usually set at 0.05 or 0.01. If the observed test statistic falls within the critical region, it means that the probability of obtaining a value as extreme or more extreme than the observed statistic is very low, assuming the null hypothesis is true. This probability is called the p-value. Therefore, you would reject the null hypothesis and conclude that there is a significant difference or relationship between the variables being studied.
To know more about t-statistic,
https://brainly.com/question/15236063
#SPJ11
Related Questions
The first term of a geometric sequence is 6 and the fourth term is 384. What is the sum of the first 10 terms of the corresponding series?
Answers
Answer:
2097150
Step-by-step explanation:
GIVEN :-
First term of G.P. = 6Forth term of G.P. = 384TO FIND :-
Sum of first 10 terms of the G.P.CONCEPT TO BE USED IN THIS QUESTION :-
Geometric Progression :-
It's a sequence in which the successive terms have same ratio.General form of a G.P. ⇒ a , ar , ar² , ar³ , ....... [where a = first term ; r = common ratio between successive terms]Sum of 'n' terms of a G.P. ⇒ \(\frac{a(r^n - 1)}{r-1}\).[NOTE :- \(\frac{a(1-r^n)}{1-r}\) can also be the formula for "Sum of n terms of G.P." because if you put 'r' there (assuming r > 0) you'll get negative value in both the numerator & denominator from which the negative sign will get cancelled from the numerator & denominator. YOU'LL BE GETTING THE SAME VALUE FROM BOTH THE FORMULAES.]
SOLUTION :-
Let the first term of the G.P. given in the question be 'a' and the common ratio between successive terms be 'r'.
⇒ a = 6
It's given that forth term is 384. So from "General form of G.P." , it can be stated that :-
\(=> ar^3 = 384\)
\(=> 6r^3 = 384\)
Divide both the sides by 6.
\(=> \frac{6r^3}{6} = \frac{384}{6}\)
\(=> r^3 = 64\)
\(=> r = \sqrt[3]{64} = 4\)
Sum of first 10 terms \(= \frac{6(4^{10}-1)}{4 - 1}\)
\(= \frac{6(1048576 - 1)}{3}\)
\(= 2 \times 1048575\)
\(= 2097150\)
Sam will take four science tests this quarter. Her scores on three of the tests are shown below. What does Sam need to score on the fourth test to ensure that she will have an average of 90% for all four tests?

Answers
Answer:
98%
Step-by-step explanation:
83%+91%+88%+?=90×4
262+?=360
?=360-262
?=98%
Answer:
98% i believe
Step-by-step explanation:
Graph the Equation 3x – 2y = -6 over the range x = -10 to x = 10. = 2) Use the Graphical method to solve the following pair of equations. 10x = 5y -3x + y = 1
Answers
Graphing the equation 3x - 2y = -6 over the range x = -10 to x = 10:
To graph the equation 3x - 2y = -6, we need to rearrange it in the form y = mx + b, where m is the slope and b is the y-intercept.
3x - 2y = -6
-2y = -3x - 6
Divide both sides by -2:
y = (3/2)x + 3
Now we have the equation in slope-intercept form.
To graph the equation, we can plot a few points and draw a line through them. Let's choose some x-values from the range -10 to 10 and find the corresponding y-values.
For x = -10:
y = (3/2)(-10) + 3
y = -15 + 3
y = -12
For x = 0:
y = (3/2)(0) + 3
y = 0 + 3
y = 3
For x = 10:
y = (3/2)(10) + 3
y = 15 + 3
y = 18
Plotting these points (-10, -12), (0, 3), and (10, 18) on the graph and drawing a line through them, we get the graph of the equation 3x - 2y = -6.
Using the graphical method to solve the pair of equations:
The given equations are:
10x = 5y
-3x + y = 1
To solve these equations graphically, we need to plot their graphs on the same coordinate plane and find the point where they intersect, which represents the solution.
Rearranging the second equation in slope-intercept form:
y = 3x + 1
Now we have the equations in the form y = mx + b.
Plotting the graphs of the equations 10x = 5y and y = 3x + 1, we can find the point of intersection, which represents the solution to the system of equations.
The point of intersection is the solution to the system of equations.
To know more about equations, visit :
brainly.com/question/12788590
#SPJ11
Fill in the blank with a constant, so that the resulting quadratic expression is the square of a binomial. \[x^2 22x \underline{~~~~}.\]
Answers
The square of a binomial, the value of the constant \(c\) should be equal to half the coefficient of the linear term squared, which in this case is \(c = \left(\frac{22}{2}\right)^2 = 121\). Therefore, the constant that needs to be filled in is 121.
To express the quadratic expression \(x^2 + 22x + c\) as the square of a binomial, we need to find a binomial of the form \((x + a)^2\) that expands to \(x^2 + 22x + c\). Expanding \((x + a)^2\) gives \(x^2 + 2ax + a^2\). Comparing the coefficients of the expanded binomial and the given quadratic expression, we can equate the linear terms to find \(2ax = 22x\), which gives \(a = 11\). Substituting this value of \(a\) back into the expanded binomial, we have \(x^2 + 22x + 121\). Therefore, the constant that needs to be filled in is 121.
know more about binomial :brainly.com/question/30339327
#SPJ11
a scientist was interested in studying if students beliefs about illegal drug use changes as they go through college. the scientist randomly selected 104 students and asked them before they entered college if they thought that illegal drug use was wrong or o.k. four years later, the same 104 students were asked if thought that illegal drug use was wrong or o.k. the scientist decided to perform mcnemar's test. the data is below. what is the null hypothesis?
Answers
In this case, the scientist is studying if students' beliefs about illegal drug use change as they go through college. The null hypothesis (H0) for McNemar's test in this context would state that there is no significant change in students' beliefs about illegal drug use between the time they enter college and four years later. In other words, the proportion of students who change their beliefs about illegal drug use is not significantly different from the proportion who do not change their beliefs.
Null hypothesis (H0): There is no significant difference in students' beliefs about illegal drug use before and after going through college.
Let F = -1 yi + 1 xj. Use the tangential vector form of Greens Theorem to compute the circulation integral int C F .dr where C is the positively oriented circle x^2 + y^2 = 1.
Answers
The circulation integral of F around the given circle is 2π. To compute the circulation integral using the tangential vector form of Green's Theorem, we first need to parameterize the circle C.
The given circle has the equation x^2 + y^2 = 1, which can be parameterized as follows:
x = cos(t)
y = sin(t)
where t is the parameter ranging from 0 to 2π.
Next, we compute the tangential vector for the parameterization:
r(t) = cos(t)i + sin(t)j
Taking the derivative of r(t) with respect to t, we get:
r'(t) = -sin(t)i + cos(t)j
Now, we can compute the circulation integral using the formula:
∮C F · dr = ∫(F · T) ds
where F is the given vector field, T is the tangential vector, and ds is the differential arc length.
Plugging in the values, we have:
F · T = (-1 yi + 1 xj) · (-sin(t)i + cos(t)j) = -sin(t)y + cos(t)x
ds = ||r'(t)|| dt = dt
Now, we integrate over the parameter t from 0 to 2π:
∫[0 to 2π] (-sin(t)y + cos(t)x) dt
= ∫[0 to 2π] (-sin(t)sin(t) + cos(t)cos(t)) dt
= ∫[0 to 2π] (-sin^2(t) + cos^2(t)) dt
= ∫[0 to 2π] (1) dt
= [t] from 0 to 2π
= 2π
Therefore, the circulation integral of F around the given circle is 2π.
Learn more about tangential vector here:
brainly.com/question/17042788
#SPJ11
what is the value of x
Answers
Answer:
The value of x is dependant on the value of y.
Step-by-step explanation:
y = (number)x + (another number)
I need a PNG or picture to give you a factual answer to the value of X.
During each week of piano lessons, Lila learns to play 2 new pieces. After 4 weeks of piano lessons, how many total pieces will Lila be able to play?
Answers
Two piano lessons a week means you just multiply two by the number of weeks
How do u calculate the percentage if it is more than 100%?
Like for example 140%
Answers
Work out the difference (increase) between the two numbers you are comparing.
Increase = New Number - Original Number.
Then: divide the increase by the original number and multiply the answer by 100.
% increase = Increase ÷ Original Number × 100.
Again I’m so sorry
a cottage is on a bearing of 200° and 110° from Dogbe's and Manu's farm respectively. If Dogbe walked 5km and Manu 3km from the cottage to their farm, find and correct to 2 s.f the distance between the two farms and correct to the nearest degree, the bearing of Manu's farm from Dogbe's
PLEASE NOTE: DOGBE AND MANU ARE NAMES
Answers
Based on the drawing obtained from the description, the location of
Manu's farm is located relatively south to Dogbe's farm.
The distance between the two farms is approximately 3.8 kmThe bearing of Manu's farm from Dogbe is approximately 238°Reasons:
The bearing of the cottage to Dogbe's farm = 200°
The distance Dogbe walks from the cottage to his farm = 5 km
The bearing of the cottage from Manu's farm = 110°
The distance Manu walks from the cottage to his farm = 3 km
Required:
The distance and between the two farms.
Solution:
Please find attached a drawing showing the position of the cottage
By cosine rule, we have;
a² = b² + c² - 2·b·c·cos(A)Where;
b = The distance Dogbe walks from the cottage to his farm = 5 km
c = The distance Manu walks to his farm from the cottage = 3 km
a = The distance between the two farms = d
A = The angle between the paths to the cottage from the farms = 50°
By plugging in the values, we have;
d² = 5² + 3² - 2 × 5 × 3 × cos(50°)
d = √(5² + 3² - 2 × 5 × 3 × cos(50°)) ≈ 3.8
The distance between the two farms, d ≈ 3.8 kmRequired:
The bearing of Manu's farm from Dogbe's
Solution:
By sine rule, we have;
\(\displaystyle \frac{3}{sin(C)} = \mathbf{ \frac{d}{sin(50^{\circ})}}\)Which gives;
\(\displaystyle sin(C) = \mathbf{\frac{3 \times sin(50^{\circ})}{\sqrt{5^2 + 3^2 - 2 \times 5 \times 3 \times cos(50^{\circ})} }}\)
\(\displaystyle \angle C = arcsine \left(\frac{3 \times sin(50^{\circ})}{\sqrt{5^2 + 3^2 - 2 \times 5 \times 3 \times cos(50^{\circ})} } \right) \approx 38 ^{\circ}\)
The bearing of Manu's farm from Dogbe's = 200° + ∠C
Therefore;
The bearing of Manu's farm from Dogbe's ≈ 200° + 38 = 238°Learn more about bearings in mathematics here:
https://brainly.com/question/10710413

The alpha level for each hypothesis test made on the same set of data is called ______.
a. testwise alpha
b. experimentwise alpha
c. pairwise comparison
d. the Bonferroni procedure
Answers
The alpha level for each hypothesis test made on the same set of data is called B. experimentwise alpha
What is experimentwise alpha?When numerous suppositions are examined concurrently, the likelihood of committing at least one type I mistake grows.
In order to manage the probability of erroneously rejecting the null hypothesis in all tests, scientists usually modify the alpha level for each test, with the purpose of maintaining an experimentwise alpha that reflects the probability of making a type I error in the entire set of tests.
The Bonferroni procedure is a technique utilized to regulate the experimentwise error rate by adjusting the alpha level for each hypothesis test.
Learn more about hypothesis at: https://brainly.com/question/606806
#SPJ1
show that the wave function y=e^(b(x-vt)) is a solution of the linear wave equation (eq. 16.27), where b is a constant
Answers
To show that the wave function y=e^(b(x-vt)) is a solution of the linear wave equation (eq. 16.27), we need to plug the wave function into the equation and see if it satisfies the equation.
The linear wave equation (eq. 16.27) is given by:
∂^2y/∂x^2 = (1/v^2) ∂^2y/∂t^2
Plugging in the wave function y=e^(b(x-vt)) into the equation, we get:
∂^2(e^(b(x-vt)))/∂x^2 = (1/v^2) ∂^2(e^(b(x-vt)))/∂t^2
Taking the second derivative with respect to x, we get:
b^2 e^(b(x-vt)) = (1/v^2) ∂^2(e^(b(x-vt)))/∂t^2
Taking the second derivative with respect to t, we get:
b^2 e^(b(x-vt)) = (1/v^2) b^2 v^2 e^(b(x-vt))
Simplifying, we get:
b^2 e^(b(x-vt)) = b^2 e^(b(x-vt))
This shows that the wave function y=e^(b(x-vt)) satisfies the linear wave equation (eq. 16.27) and is therefore a solution of the equation.
Learn more about the linear wave equation : https://brainly.com/question/25699025
#SPJ11
janet can make 4/5 of a necklace in 20 min .how many necklaces can she make in 1 hour

Answers
4/5 * 3 = 12/5
20 * 3 = 1 hour = 60 min
factor the trinomial below. x^2+13x+42
Answers
Answer:
(x + 6)(x + 7)
Step-by-step explanation:
To factor the trinomial x^2 + 13x + 42, we need to find two numbers that multiply to 42 and add up to 13.
One way to do this is to list all the pairs of factors of 42 and see which pair adds up to 13:
1, 42 -> 1 + 42 = 43
2, 21 -> 2 + 21 = 23
3, 14 -> 3 + 14 = 17
6, 7 -> 6 + 7 = 13
So the pair of factors that we want is 6 and 7. We can use these numbers to rewrite the middle term of the trinomial:
x^2 + 13x + 42 = x^2 + 6x + 7x + 42
Next, we can group the first two terms and the last two terms:
x^2 + 6x + 7x + 42 = (x^2 + 6x) + (7x + 42)
Now, we can factor out the greatest common factor from each group:
x(x + 6) + 7(x + 6)
Notice that we have a common factor of (x + 6) in both terms. We can factor this out:
(x + 6)(x + 7)
if you help me it would be a great favor of you

Answers
Answer:
Step-by-step explanation:
Weight of one fruit fly = \(\frac{1.3*10^{2}}{1*10^{6}}\)
\(=1.3*10^{2-6}\\\\=1.3*10^{-4}\)
4)
\(1.674*10^{-27}\) > \(1.672*10^{-27}\) > 9.109 * \(10^{-31}\)
Electron has the least negative exponent. So, it is the lightest
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP ASAP

Answers
Answer:
70 degrees total degree 540
Using the Definitional proof, show that each of these functions is O(x2). (a) f(x) = x (b) f(x) = 9x + 5 (c) f(x) = 2x2 + x + 5 (d) f(x) = 10x2 + log(x)
Answers
To show that each function is O(x^2) using the Definitional proof, we need to find a constant c and a positive number k such that |f(x)| ≤ c|x^2| for all values of x greater than some value k.
(a) For function f(x) = x:
We need to find a constant c and k such that |x| ≤ c|x^2| for all x > k.
Let's choose c = 1 and k = 1.
|f(x)| = |x| ≤ 1 * |x^2| for all x > 1.
Therefore, f(x) = x is O(x^2).
(b) For function f(x) = 9x + 5:
We need to find a constant c and k such that |9x + 5| ≤ c|x^2| for all x > k.
Let's choose c = 14 and k = 1.
|f(x)| = |9x + 5| ≤ 14 * |x^2| for all x > 1.
Therefore, f(x) = 9x + 5 is O(x^2).
(c) For function f(x) = 2x^2 + x + 5:
We need to find a constant c and k such that |2x^2 + x + 5| ≤ c|x^2| for all x > k.
Let's choose c = 8 and k = 1.
|f(x)| = |2x^2 + x + 5| ≤ 8 * |x^2| for all x > 1.
Therefore, f(x) = 2x^2 + x + 5 is O(x^2).
(d) For function f(x) = 10x^2 + log(x):
We need to find a constant c and k such that |10x^2 + log(x)| ≤ c|x^2| for all x > k.
Let's choose c = 11 and k = 1.
|f(x)| = |10x^2 + log(x)| ≤ 11 * |x^2| for all x > 1.
Therefore, f(x) = 10x^2 + log(x) is O(x^2).
In each case, we have found a constant c and a value k such that the inequality |f(x)| ≤ c|x^2| holds for all x greater than k. This satisfies the definition of f(x) being O(x^2).
To learn more about function click here:
brainly.com/question/30721594
#SPJ11
find the midpoint of the line segment joining the points (5 -3) and (-1 7)
Answers
Answer:
Step-by-step explanation:
(5 - 1)/2 4/2= 2
(-3 + 7)/2= 4/2= 2
(2, 2) is the midpoint
Round to the nearest tenth
Find x.

Answers
9514 1404 393
Answer:
73.4°
Step-by-step explanation:
The relevant trig relation is ...
Sin = Opposite/Hypotenuse
sin(x°) = 23/24
x° = arcsin(23/24) ≈ 73.4°
Which function represents the graph of y=x^2 after it has been translated 4 units to the left?
options:
y=(x-4)^2 or y=(x+4)^2
Answers
Answer:
oh.. maybe you can install photomath
Answer:
y=(x+4)^2
Step-by-step explanation:
A trick I use is if it is a plus sign then it goes left, if it is a minus sign then it goes right.
Help ASAP!!!!! ILL GIVE BRANILYLEST!

Answers
Answer: Area: (100+75π/2)cm^2 Perimeter: (10+75π/2)cm
Step-by-step explanation:
Area of total shape
= square+3 semi-circles
=100cm^2 + 5*5πcm^2*3/2 = 100cm^2+75/2*πcm^2
= (100+75π/2)cm^2
Perimeter of shape
= 10cm + 25/2π*3cm
= (10+75π/2)cm
Step-by-step explanation:
in this figure you can observe 1 cube and 3 half cirles
the flield of the square would by using a formula a(lenght) * b(height)
in this case it would be 10m * 10m = 100m
and the formula for a cirle would be
A = pir^2
knowing that we can connect two of the halfs and make a cirle with a radius of 5
A= pi 5^2
A= pi 25
25pi approximatly equals to 78.53982m
knowing that information we can devide that value by 2 and get the value of the 3rd half cirlce
which is 39.26991m
than we add all the values we collected
39.26991m + 78.53982m + 100m = 217.80973 m
Use factoring to solve
2x^2-17x-35=0
Answers
Answer:
This does not factor
Step-by-step explanation:
2x^2-17x-35=0
Since the x^2 has a coefficient of 2
(2x ) ( x )
Looking at the factors of -35
-1 35 1, -35
-5 7 5, -7
We need to get to -17
You cannot factor this
-
(√5-3√2)^2 simplify please help
Answers
Answer:
Step-by-step explanation:
To simplify the expression (√5-3√2)^2, we can use the formula for squaring a binomial:
(a - b)^2 = a^2 - 2ab + b^2
In this case, we have:
a = √5
b = 3√2
So we can substitute these values into the formula:
(√5 - 3√2)^2 = (√5)^2 - 2(√5)(3√2) + (3√2)^2
Simplifying, we get:
(√5 - 3√2)^2 = 5 - 6√10 + 18
= 23 - 6√10
Therefore, (√5 - 3√2)^2 simplifies to 23 - 6√10.
Answer: 23 - 6√10
Step-by-step explanation:
(√5 - 3√2)² ⇒ 5 - 6√10 + 18 ⇒ 5 - 6√10 + 18 ⇒ 23 - 6√10
Use the following data to calculate the cost of goods sold for the period: \[ \begin{array}{l} \$ \angle D U, 0 U U . \\ \$ 246,800 \text {. } \\ \$ 242,800 \text {. } \\ \$ 258,800 . \end{array} \]
Answers
The cost of goods sold for the period is $748,400.By accurately calculating the cost of goods sold, businesses can make informed decisions regarding pricing, inventory management, and overall financial performance.
To calculate the cost of goods sold (COGS), we add up the values provided in the data:
COGS = $246,800 + $242,800 + $258,800
= $748,400
The cost of goods sold for the period, based on the given data, is $748,400. The COGS represents the direct costs incurred by a company to produce the goods sold during a specific period. It includes the cost of raw materials, direct labor, and other direct production expenses.
Accurately calculating the COGS is crucial for financial analysis and decision-making. By subtracting the COGS from the total sales revenue, we obtain the gross profit, which is a key indicator of a company's profitability. The COGS also helps determine the company's gross margin, which indicates the percentage of revenue that remains after accounting for the cost of producing goods.
For effective inventory management, it is important for businesses to monitor and control their COGS. It allows them to assess the efficiency of their production processes, identify cost-saving opportunities, and evaluate pricing strategies. Additionally, tracking the COGS helps businesses determine the profitability of specific product lines or services.
The COGS provides valuable insights into a company's operational efficiency and profitability.
To know more about cost , visit;
https://brainly.com/question/19261126
#SPJ11
use a power series to approximate the definite integral to 6 decimal places\intx^2/(1+x^4) dx with the integral from 0 t0 1/2
Answers
0.092011 is an approximation of the definite integral of x^2/(1+x^4) from 0 to 1/2 up to 6 decimal places.
In summary, to approximate the definite integral of x^2/(1+x^4) from 0 to 1/2 using a power series, we can use the geometric series formula to expand the denominator, integrate the resulting power series term by term, and then evaluate the resulting series up to a certain number of terms to obtain an approximation of the integral to a desired degree of accuracy.
To begin, we can use the formula for a geometric series to write the denominator as:
1/(1+x^4) = 1 - x^4 + x^8 - x^12 + ...
We can then multiply the numerator x^2 by this series and integrate term by term to obtain:
∫x^2/(1+x^4) dx = ∫[x^2 - x^6 + x^10 - x^14 + ...] dx
= (1/3)x^3 - (1/7)x^7 + (1/11)x^11 - (1/15)x^15 + ...
To approximate the integral up to 6 decimal places, we can evaluate this series up to a certain number of terms, say the first 10 terms:
(1/3)(1/2)^3 - (1/7)(1/2)^7 + (1/11)(1/2)^11 - (1/15)(1/2)^15 + ...
= 0.092011
This is an approximation of the definite integral of x^2/(1+x^4) from 0 to 1/2 up to 6 decimal places.
To learn more about definite integral click here, brainly.com/question/30760284
#SPJ11
30 treadmils to 36 elliptical machines
Answers
Answer:
5/6 is the simplest form
Hope that helps
In a geometry class, students are asked to describe the dimensions of a plane based on the components that create a plane. Which student’s response is correct?
Answers
B. Stacy states that a plane has two dimensions because it is made up of an infinite number of lines is the correct answer
amy needs to mail a usb drive to a friend. she uses 41-cent stamps and 7-cent stamps to pay $1.79 in postage. how many of each stamp did amy use?
Answers
So, Amy used 30 stamps of 41-cent stamps and 17 stamps of 7-cent stamps.
This is a system of equations problem. We can call the number of 41-cent stamps x and the number of 7-cent stamps y.
The two equations are:
x + y = total number of stamps used
0.41x + 0.07y = 1.79 (the total cost of the postage in dollars)
We can use the first equation to solve for one of the variables in terms of the other. For example, we can solve for y in terms of x:
y = total number of stamps used - x
Then we can substitute this into the second equation:
0.41x + 0.07(total number of stamps used - x) = 1.79
Solving for x,
x = (1.79 - 0.07*total number of stamps used) / 0.41
We can substitute this into the first equation to solve for total number of stamps used.
x + y = total number of stamps used
x + (total number of stamps used - x) = total number of stamps used
2x = 1.79/0.41 + 0.07/0.41
x = (1.79/0.41 + 0.07/0.41)/2
x = (1.79 + 0.07)/(0.41*2)
So, x = 30 stamps of 41-cent stamps
and y = (total number of stamps used - x) = (total number of stamps used - 30) = (1.79/0.48 - 30) = 17 stamps of 7-cent stamps
So, Amy used 30 stamps of 41-cent stamps and 17 stamps of 7-cent stamps.
To learn more about equations
Visit; brainly.com/question/29657983
#SPJ4
PLEASE HELP WILL GIVE U BRAINLIEST TYYY
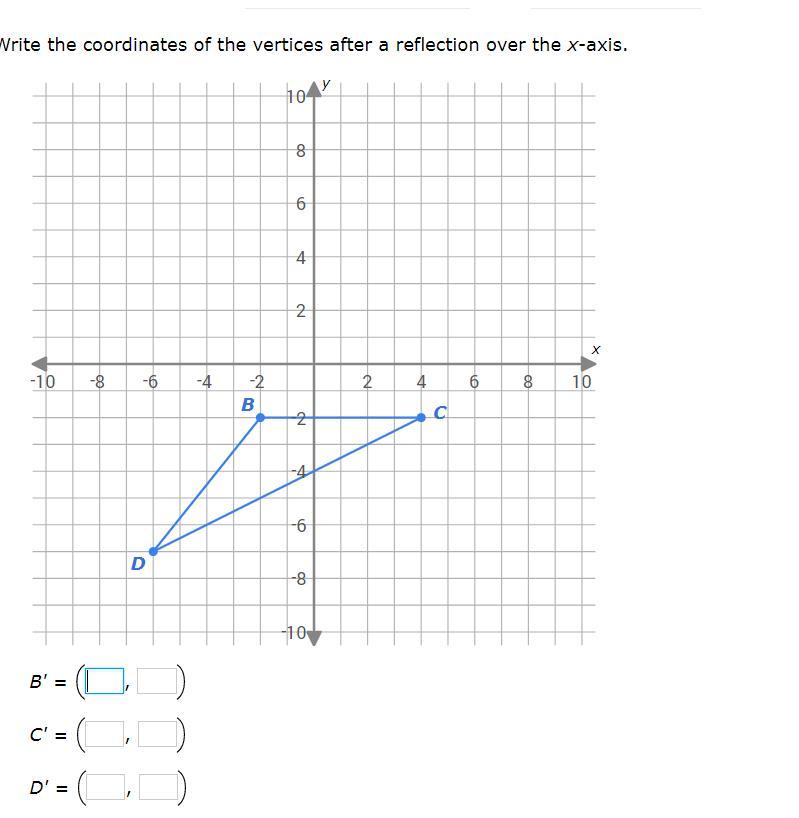
Answers
Answer: b(-2, 2) c(4,2) d (-6,7)
Step-by-step explanation:
The formula for reflecting over x axis is (x,y) - > (x,-y)
the current points are
-2,-2
4, -2
-6, -7
which turn into -2, 2
4, 2
-6,7
can someone help me with this question

Answers
To minimize the cost of the package:
Radius = 3.86 cm.
Height = 9.62 cm.
Minimum cost = 14.01 cents.
How to calculate the volume of a cylinder?In Mathematics and Geometry, the volume of a cylinder can be calculated by using the following formula:
Volume of a cylinder, V = πr²h
Where:
V represents the volume of a cylinder.h represents the height of a cylinder.r represents the radius of a cylinder.By substituting the given parameters into the formula for the volume of a cylinder, we have the following;
450 = πr²h
h = 450/πr²
For the surface area of this cylinder, we have:
SA = 2πrh + 2πr²
By substituting the height (h) in terms of r, we have:
SA = 2πr(450/πr²) + 2πr²
SA = 900/r + 2πr²
Assuming the radius of the paper top is denoted by r, and the height of this cylinder is either greater than or equal to the radius of the paper top, so that the top can be completely covered with paper. Therefore, the cost of the container is given by:
Cost, C = 0.02(2πrh + πr²) + 0.08(πr²)
Cost, C = 0.04πr(900/πr²) + 0.02πr² + 0.08πr²
Cost, C = 36/r + 0.02πr² + 0.08πr²
Cost, C = 36/r + 0.1πr²
In order to minimize the cost, we have to find the values of r that minimizes the cost function, C, by taking the partial derivatives of C with respect to r, and then equate to zero:
dC/dr = -36/r² + 0.2πr = 0
36/r² = 0.2πr
r³ = 36/0.2π
r = ∛(36/0.628)
r = ∛(57.3248)
r = 3.86 cm.
h = 450/πr²
h = 450/(3.14 × 3.86²)
Height, h = 9.62 cm.
Minimum cost, C = 36/3.86 + 0.1π(3.86)²
Minimum cost, C = 9.33 + 4.68
Minimum cost, C = 14.01 cents.
Read more on cylinder here: brainly.com/question/14060443
#SPJ1