In a survey of 3475 adults, 1440 say they have started paying bills online in the last year. Construct a 99% confidence interval for the population proportion. Interpret the results. A 99% confidence interval for the population proportion is ( ), ( ). (Round to three decimal places as needed.) Interpret your results. Choose the correct answer below.
a. With 99% confidence, it can be said that the population proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
b. With 99% confidence, it can be said that the sample proportion of adults who say they have started paying bills online in the last year is between the endpoints of the given confidence interval.
Answers
Related Questions
8.In a lottery game, a person must select 5 numbers from a total of 40. Tracy has chosen 7, 8, 9, 10, 11. Jaime has chosen 39, 17, 37, 5, 28. Who has a greater chance of winning
Answers
a grain silo has a cylindrical shape. its radius is 9ft, and height is 52ft. what is the volume of the silo?use the value of 3.14 for pieround to the nearest whole number
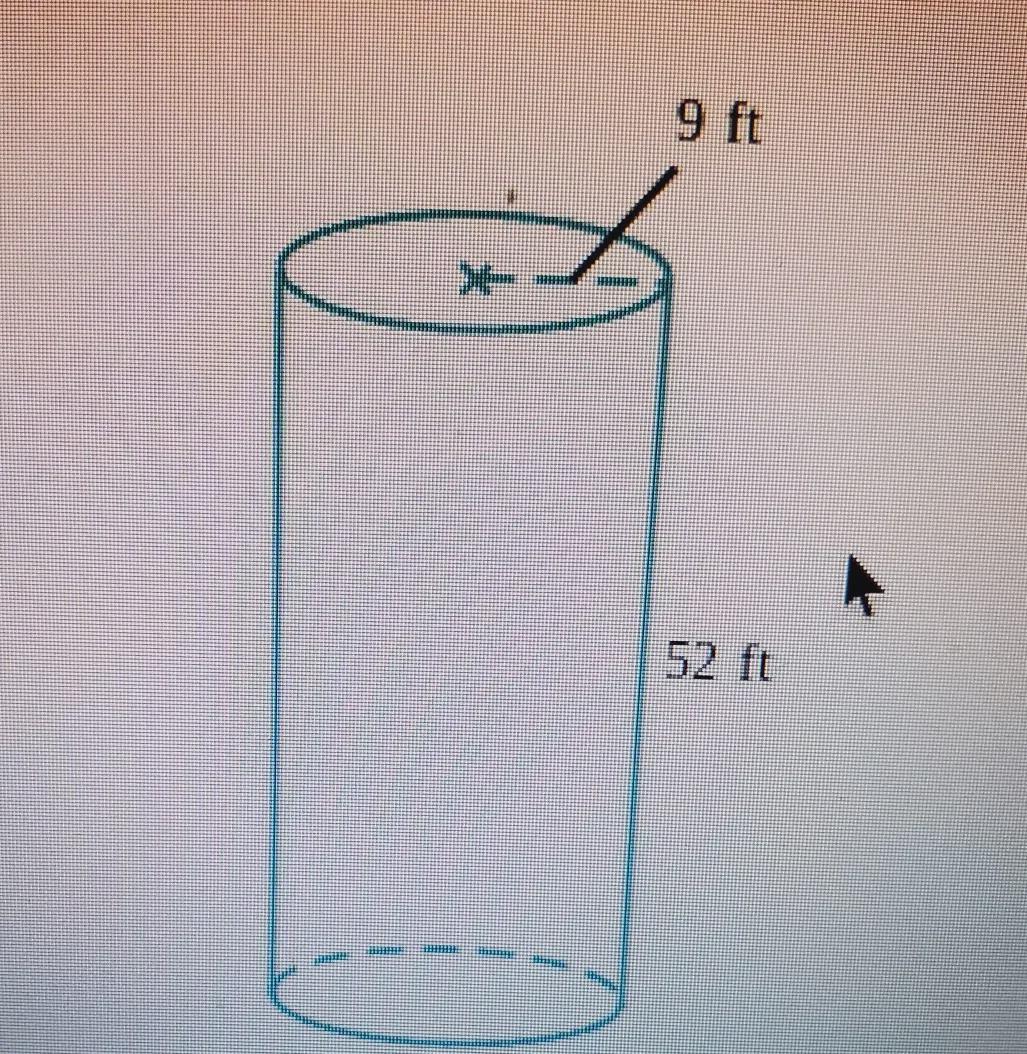
Answers
Given:
Radius = 9 ft
Height = 52 ft
Volume of cylindrical (silo) is:
\(\text{Volume}=\pi r^2h\)\(\begin{gathered} r=9 \\ h=52 \\ \pi=3.14 \end{gathered}\)\(\begin{gathered} \text{Volume}=\pi r^2h \\ =3.14\times(9)^2\times52 \\ =3.14\times81\times52 \\ =254.34\times52 \\ =13225.68 \end{gathered}\)Nearst whole number is 13226
Two student clubs were selling t-shirts and school notebooks to raise money for an upcoming school event. In the first few minut
notebooks, and made $19. Club B sold 1 t-shirt and 1 notebook, for a total of $8.
-
Use matrices to solve the equation and determine the cost of a t-shirt and the cost of a notebook. Show or explain all necessary:

Answers
Using matrices the simultaneous equation is solved to get x = 3 and y = 5
How to solve the simultaneous equation using matricesThis method required finding determinants in three occasions then dividing
The given equation
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right] \left[\begin{array}{c}x\\y\\\end{array}\right]= \left[\begin{array}{c}19\\8\\\end{array}\right]\)
the determinant is
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right]\)
3 * 1 - 2 * 1 = 3 - 2 = 1
Solving for x
determinant while replacing x values
\(\left[\begin{array}{cc}19&2&\\8&1\\\end{array}\right]\)
19 * 1 - 2 * 8 = 19 - 16 = 3
solving for x = 3/1 = 3
Solving for y
determinant while replacing y values
\(\left[\begin{array}{cc}3&19&\\1&8\\\end{array}\right]\)
3 * 8 - 19 * 1 = 24 - 19 = 5
solving for y = 5/1 = 5
Learn more about simultaneous equations at:
https://brainly.com/question/148035
#SPJ1
Decide whether parallelogram JKLM is a rectangle, a rhombus, or a square. Give all names that apply.
J(3, 1), K(3, — 3), L(-2, -3), M( − 2, 1)
Orectangle
Orhombus
square
Explain your reasoning.
O The sides are perpendicular and not congruent.
O The diagonals are perpendicular but not congruent.
O The sides are congruent and not perpendicular.
The diagonals are congruent and perpendicular.

Answers
the parallelogram JKLM is a square.
What is square?
Having four equal sides, a square is a quadrilateral. There are numerous square-shaped objects in our immediate environment. Each square form may be recognized by its equal sides and 90° inner angles. A square is a closed form with four equal sides and interior angles that are both 90 degrees. Numerous different qualities can be found in a square.
We are given that rajiv wishes to make a cube without lid with cardboard.
JM = -5² = 25
KL = -5² = 25
JK = -4²=16
LM =-4²=16
So, the parallelogram JKLM is a square.
Learn more about square, by the following link.
brainly.com/question/25092270
#SPJ1
Atul gets a pocket money allowance of Rs.120 per day. Thinking that this was rather less he asked his friends about their allowances and obtained the following data which includes his allowance also ( Amount I Rs.) 120, 180, 100, 50, 250, 200,200,220, 150, 100,100,150,130,200,180, 100, 150, 100, 180, 150, 120, 150, 100, 150, 100, 120, 180, 200, 50.
He presented this data to his father and asked for an increase in his allowance as he was getting less than average amount. His father, a statistician, countered pointing out that Atul's allowance was actually more than the average amount.
Answers
Atul's father is mistaken, and Atul's request for an increase in his allowance may be valid based on the information given.
What is Statistics?Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data.
To determine whether Atul's allowance is above or below the average, we need to calculate the average allowance for all the friends, including Atul.
To do his, we add up all the amounts and divide by the total number of friends:
Average allowance = (120+180+100+50+250+200+200+220+150+100+100+150+130+200+180+100+150+100+180+150+120+150+100+150+100+120+180+200+50) / 29
Average allowance = 162.07
So, the average allowance for Atul's friends, including himself, is Rs. 162.07 per day.
Since Atul's allowance is Rs. 120 per day, we can see that his allowance is actually less than the average.
Therefore, Atul's father is mistaken, and Atul's request for an increase in his allowance may be valid based on the information given.
To learn more on Statistics click:
https://brainly.com/question/29093686
#SPJ9
Solve by graphing. x2 + 2x – 3 = 0
Answers
By graphing or visualizing the parabolic shape, we can observe where the graph intersects the x-axis, which represents the solutions to the equation. In this case, the solutions are x = -3 and x = 1.
To solve the quadratic equation x^2 + 2x - 3 = 0 by graphing, we can plot the graph of the equation and find the x-values where the graph intersects the x-axis.
First, let's rearrange the equation to the standard form: x^2 + 2x - 3 = 0.
We can create a graph by plotting points for different values of x and then connecting them. However, I can describe the process and the key points on the graph.
1. Find the x-intercepts: These are the points where the graph intersects the x-axis. To find them, set y (the equation) equal to zero and solve for x:
0 = x^2 + 2x - 3.
This quadratic equation can be factored as (x + 3)(x - 1) = 0.
Therefore, x = -3 or x = 1.
2. Plot the points: Plot the points (-3, 0) and (1, 0) on the graph. These are the x-intercepts.
3. Draw the graph: The graph of the equation x^2 + 2x - 3 = 0 is a parabola that opens upward. It will pass through the x-intercepts (-3, 0) and (1, 0).
For more such questions on graph
https://brainly.com/question/19040584
#SPJ8
James wants to have earned $6,180 amount of interest in 28 years. Currently he finds
that his annual interest rate is 6.12%. Calculate how much money James needs to invest
as his principal in order to achieve this goal.
Answers
Answer:
$3606.44
Step-by-step explanation:
The question asks us to calculate the principal amount that needs to be invested in order to earn an interest of $6180 in 28 years at an annual interest rate of 6.12%.
To do this, we need to use the formula for simple interest:
\(\boxed{I = \frac{P \times R \times T}{100}}\),
where:
I = interest earned
P = principal invested
R = annual interest rate
T = time
By substituting the known values into the formula above and then solving for P, we can calculate the amount that James needs to invest:
\(6180 = \frac{P \times 6.12 \times 28}{100}\)
⇒ \(6180 \times 100 = P \times 171.36\) [Multiplying both sides by 100]
⇒ \(P = \frac{6180 \times 100}{171.36}\) [Dividing both sides of the equation by 171.36]
⇒ \(P = \bf 3606.44\)
Therefore, James needs to invest $3606.44.
(GIVING BRAINLIEST!!)
A cake is cut into 6 equal-sized pieces. Each piece is one sixth of the whole. Choose the equation that represents this fraction.
A) 5 ÷ 6 = ________
B) 6 ÷ 5 = ________
C) 1 ÷ 6 = ________
D) 6 ÷ 1 = ________
Answers
Answer:
c is correct
Step-by-step explanation:
The equation that represents this fraction is 1 ÷ 6 =1/6. Therefore, option C is the correct answer.
What is the fraction?In Mathematics, fractions are represented as a numerical value, which defines a part of a whole. A fraction can be a portion or section of any quantity out of a whole, where the whole can be any number, a specific value, or a thing.
Given that, a cake is cut into 6 equal-sized pieces. Each piece is one sixth of the whole.
The equation is 1 ÷ 6 =1/6
Therefore, option C is the correct answer.
To learn more about the fraction visit:
brainly.com/question/1301963.
#SPJ2
When money is spent on goods and services, those who receive the money also spend some of it. The people receiving some of the twice-spent money will spend some of that, and so on. Economists call this chain reaction the multiplier effect. In a hypothetical isolated community, the local government begins the process by spending D dollars. Suppose that each recipient of spent money spends 100c% and saves 100s% of the money that he or she receives. The values c and s are called the marginal propensity to consume and the marginal propensity to save and, of course, course, c + s = 1. Let Sn be the total spending that has been generated after n transactions.
Required:
Find an equation for Sn.
Answers
Solution :
If \(S_n\) is the total spending generated after n transactions, then \(a_n\) is the spending generated during the n-th transaction. Since the government spends D dollars, then \(a_1\) = D.
Then the second person will receive D dollars and spend \(D_c\) dollars. Therefore, \(a_2=D_c\). The next person will receive \(D_c\) dollars, which means they are spending \(a_3 = (D_c)c = Dc^2\) dollars. Therefore,
\(a_1 = D\)
\(a_2=D_c\)
\(a_3 = Dc^2\)
\(a_4 = (Dc^2)c= Dc^3\)
....
\(a_n=Dc^{n-1}\)
∴ \(S_n=a_1+a_2+a_3+....+a_n\)
\(S_n = D+Dc+Dc^2+Dc^3+...+Dc^{n-1}\)
\(S_n= D(1+c+c^2+...+c^{n-1})\)
\(S-n=D . \frac{1-c^n}{1-c}\)
Find the measure of each marked angle. Assume the lines are parallel.
x+1=°
O
4x-26=
(Simplify your answers. Type an integer or a fraction.)
fars
(x+1)°
(4x-26)°

Answers
The angles are 42⁰ and 138⁰.
What is Alternate interior angle?Alternate interior angles lie on the interior side of the parallel lines and are on the opposite side of the transversal.
Here, the given alternate interior angles are:
(x+1)⁰ and (4x - 26)⁰
Sum of alternate interior angle is 180⁰.
(x+1)⁰ + (4x - 26)⁰ = 180⁰
x + 1 + 4x - 26 = 180
5x - 25 = 180
5x = 180 + 25
5x = 205
x = 205 / 5
x = 41
then, (x+1)⁰ = (41+1)⁰ = 42⁰
and (4x-26)⁰ = (4 X 41 - 26)⁰
= (164 - 26)⁰
= 138⁰
Thus, the angles are 42⁰ and 138⁰.
Learn more about alternate interior angle from:
https://brainly.com/question/14693114
#SPJ1
PLEASE ANSWER WITH STEP BY STEP
SCHOOL SUPPLIES Jaime bought a notebook and a box of pencils for $5.00. The notebook cost $3.00 and there are 10 pencils in a box. The equation 3+10p=5 can be used to find the cost of one pencil. Select all equations that are equivalent.
Multiple select question.
A)
10p=8
B)
10p=2
C)
p=0.80
D)
p=0.20
E)
p=20
F)
p=80
Answers
Answer:
D and B
Step-by-step explanation:
The solution to 3+10p=5 is 0.20. The equation 10p=2 is just the equation after subtracting 3 from 5, and it also comes out as 0.20. I hope this helps!
The solution to 3+10p=5 is 0.20. The equation 10p=2 is just the equation Therefore, D and B are the correct option.
What is a system of equations?A system of equations is two or more equations that can be solved to get a unique solution. the power of the equation must be in one degree
Jaime bought a notebook and a box of pencils for $5.00.
The notebook cost $3.00 and there are 10 pencils in a box.
The equation 3+10p=5 can be used to find the cost of one pencil. S
Let's represent notebooks with "N" and pencils with "P".
Then,
3+10p = 5
10 p = 5- 3
10 p = 2
Since 10p=2, we can substitute that directly into the equation:
p = 0.20
Therefore, D and B are the correct option.
Learn more about equations here;
https://brainly.com/question/10413253
#SPJ2
Ryan runs cross-country. The equation d = 200t models the distance, d, in meters Ryan runs in t minutes. Use the equation to complete the table. A = type your answer... B = type your answer... C = type your answer... D = type your answer... Time (t) 0 1 2 3 Distance (d) A MUA
Answers
The numeric values of the function modeled by the proportional relationship d = 200t are given as follows:
t = 0, A = 0.t = 1, B = 200.t = 2, C = 400.t = 3, D = 600.How to calculate the numeric value of a function or of an expression?To calculate the numeric value of a function or of an expression, we substitute each instance of any variable or unknown on the function by the value at which we want to find the numeric value of the function or of the expression presented in the context of a problem.
The function for this problem is given as follows:
d = 200t.
Hence the numeric values of the function are given as follows:
t = 0, A = 0. -> 200 x 0 = 0.t = 1, B = 200. -> 200 x 1 = 200.t = 2, C = 400. -> 200 x 2 = 400.t = 3, D = 600. -> 200 x 3 = 600.Learn more about the numeric values of a function at brainly.com/question/28367050
#SPJ1
32 = 25t ^ 2 - 4 round to the nearest tenth
Answers
Answer:
t = 1.2, -1.2
32 + 4 = 25t^2
36 = 25t^2
Root of 36 = root of 25t
6 = 5t
6/5 = t
Therefore t = +-1/2 or +-6/5
data consist of weights in grams the unit for population standard deviation would be
Answers
Answer: s squared.s2.sigma i think
Step-by-step explanation:
Find value of x in trapezoid

Answers
Answer:
x = 1
Step-by-step explanation:
You want to know the value of x in the trapezoid with adjacent angles (43x+2)° and 135°.
Supplementary anglesThe two marked angles can be considered "consecutive interior angles" where a transversal crosses parallel lines. As such, they are supplementary.
(43x +2)° +135° = 180°
43x = 43 . . . . . . . . . . . . . . divide by °, subtract 137
x = 1 . . . . . . . . . . . . . . . divide by 43
The value of x is 1.
__
Additional comment
Given that the figure is a trapezoid, we have to assume that the top and bottom horizontal lines are the parallel bases.
<95141404393>
from a point 1.75 m above the ground and 10 m away from a tower the angle of elevation of a top of a tower is 60 degree calculate the height of the tower
Answers
Answer:
17.32 meters
Step-by-step explanation:
Let’s call the height of the tower H. The distance from the point to the base of the tower is 10 m. The angle of elevation from the point to the top of the tower is 60 degrees.
Using trigonometry, we can calculate that:
tan (60) = H / 10
H = 10 * tan (60)
H = 10 * √3
H = 17.32 m
Therefore, the height of the tower is 17.32 meters.
Let me know if I helped :)
Khan Academy grade 7th
Find the slope

Answers
Answer:
Slope = 3
Step-by-step explanation:
The slope is m in the picture.

Answer:
The slope is 3
Step-by-step explanation:
we use the equation : \(m=\frac{y2 - y1}{x2 - x1} = \frac{?}{?} =(simplify)\frac{?}{?}\) to find the slope so when we use the equation it should look like this: \(m=\frac{8-2}{(-2)-(-4)} =\frac{6}{2} =(simplify) 3\)
Given: m space measured angle space C space equals space 76, a = 20, and b = 13. What is the length of c to the nearest tenth?
Answers
Based on the given parameters, the length of c is 8.0 units
How to determine the side length of c?The given parameters are
Angle c = 76 degrees
Side a = 20
Side b = 13
The length of c is then calculated using the following law of sines
c^2 = a^2 + b^2 - 2absin(C)
Substitute the known values in the above equation
So, we have
c^2 = 20^2 + 13^2 - 2 * 20 * 13 * sin(76)
Express 20^2 as 400
c^2 = 400 + 13^2 - 2 * 20 * 13 * sin(76)
Express 13^2 as 169
c^2 = 400 + 169 - 2 * 20 * 13 * sin(76)
Evaluate the product and sin(76)
c^2 = 400 + 169 - 520 * 0.9703
Evaluate the product
c^2 = 400 + 169 - 504.55
Evaluate the exponents
c^2 = 400 + 169 - 504.55
So, we have
c^2 = 64.45
Evaluate the square root
c = 8.0
Hence, the length of c is 8.0 units
Read more about law of sines at:
https://brainly.com/question/16955971
#SPJ1
Write a linear equation to describe the number pattern that starts with 3 and continues with positive odd integers.
Answers
In order to have a linear equation, you have to write an equation like
\(y=mx+q\)
The sequence has to start with 3, so we must choose \(q=3\), because this guarantees that when \(x=0\) we have
\(y=0\cdot m + 3 =3\)
Now, \(m\) must be even. In fact, if \(m\) is even, \(mx\) will always be even for every possible \(x\), and \(mx+3\) will be odd.
So, for example, you might choose
\(y=2x+3\)
Which will produce the following sequence:
\(\begin{array}{c|c}x&f(x)\\0&3\\1&5\\2&7\\3&9\end{array}\)
and so on
Let P(x) be a predicate in the domain consisting of just the numbers 0 and 1. Let p be the statement P(0) and let q be the statement P(1).
(a) Write (∀x)P(x) as a propositional logic formula using p and q.
(b) Write (Ǝx)P(x) as a propositional logic formula using p and q.
(c) In this situation, which derivation rule from propositional logic corresponds to the universal and existential negation rules of predicate logic?
Answers
(∀x)P(x) can be written as p ∧ q, (Ǝx)P(x) can be written as ¬p ∨ ¬q, and the universal and existential negation rules of predicate logic correspond to the DeMorgan's law of propositional logic, which states that ¬(p ∨ q) = ¬p ∧ ¬q.
a) The statement (∀x)P(x) states that P(x) is true for all x in the domain, which consists of just 0 and 1. So, if P(0) is true, represented by p, and P(1) is true, represented by q, then (∀x)P(x) is true. Therefore, (∀x)P(x) can be written as p ∧ q.
b) The statement (Ǝx)P(x) states that P(x) is true for at least one x in the domain, which consists of just 0 and 1. So, if either P(0) is true, represented by p, or P(1) is true, represented by q, then (Ǝx)P(x) is true. Therefore, (Ǝx)P(x) can be written as p ∨ q.
c) The negation of (∀x)P(x), represented as ¬(∀x)P(x), is equivalent to the negation of (∀x)P(x) in predicate logic, represented as (Ǝx)¬P(x). This corresponds to DeMorgan's law of propositional logic, which states that ¬(p ∧ q) = ¬p ∨ ¬q.
Similarly, the negation of (Ǝx)P(x), represented as ¬(Ǝx)P(x), is equivalent to the negation of (Ǝx)P(x) in predicate logic, represented as (∀x)¬P(x). This corresponds to DeMorgan's law of propositional logic, which states that ¬(p ∨ q) = ¬p ∧ ¬q.
To know more about DeMorgan's law, here
https://brainly.com/question/13265106
#SPJ4
please help homework. ignore the green that's just pre algebra above

Answers
When it's simplified you get -2x + 8
Therefore the answer will be -2x + 8.
The mean June midday temperature in Desertville is 36°C and the standard deviation is 3°C.Assuming this data is normally distributed, how many days in June would you expect the midday temperature to be between 39°C and 42°C?
Answers
Answer:
The value is \(E(X) = 4 \ days\)
Step-by-step explanation:
From the question we are told that
The mean is \(\mu = 36^oC\)
The standard deviation \(\sigma = 3^oC\)
Generally the probability that in June , the midday temperature is between
39°C and 42°C is mathematically represented as
\(P(39 < X < 42) = P(\frac{39 - 36}{3} < \frac{X - \mu }{\sigma} < (\frac{42 - 36}{3} )\)
\(\frac{X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ X )\)
\(P(39 < X < 42) = P(1 < Z <2 )\)
=> \(P(39 < X < 42) = P(Z < 2) - P( Z <1 )\)
From the z table the area under the normal curve to the left corresponding to 1 and 2 is
P(Z < 2) = 0.97725
and
P(Z < 1) = 0.84134
\(P(39 < X < 42) = 0.97725 - 0.84134\)
=> \(P(39 < X < 42) = 0.13591\)
Generally number of days in June would you expect the midday temperature to be between 39°C and 42°C
\(E(X) = n * P(39 < X 42 )\)
Here n is the number of days in June which is n = 30
\(E(X) = 30 * 0.13591\)
=> \(E(X) = 4 \ days\)
NO LINKS!!! URGENT HELP PLEASE!!!
State if the given functions are inverses.
1. g(x) = 4 + (7/2)x
f(x) = 5 - (4/5)x
Find the inverses of each function.
2. g(n) = (8/3)n + 7/3
3. g(x) = 1 - 2x^3
Answers
Answer:
1) The functions are not inverses.
\(\textsf{2)} \quad g^{-1}(n)=&\dfrac{3}{8}n-\dfrac{7}{8}\)
\(\textsf{3)} \quad g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\)
Step-by-step explanation:
Question 1The inverse composition rule states that if two functions are inverses of each other, then their compositions result in the identity function.
Given functions:
\(g(x) = 4 + \dfrac{7}{2}x \qquad \qquad f(x) = 5 - \dfrac{4}{5}x\)
Find g(f(x)) and f(g(x)):
\(\begin{aligned} g(f(x))&=4+\dfrac{7}{2}f(x)\\\\&=4+\dfrac{7}{2}\left(5 - \dfrac{4}{5}x\right)\\\\&=4+\dfrac{35}{2}-\dfrac{14}{5}x\\\\&=\dfrac{43}{2}-\dfrac{14}{5}x\\\\\end{aligned}\) \(\begin{aligned} f(g(x))&=5 - \dfrac{4}{5}g(x)\\\\&=5 - \dfrac{4}{5}\left(4 + \dfrac{7}{2}x \right)\\\\&=5-\dfrac{16}{5}-\dfrac{14}{5}x\\\\&=\dfrac{9}{5}-\dfrac{14}{5}x\end{aligned}\)
As g(f(x)) or f(g(x)) is not equal to x, then f and g cannot be inverses.
\(\hrulefill\)
Question 2To find the inverse of a function, swap the dependent and independent variables, and solve for the new dependent variable.
Calculate the inverse of g(n):
\(\begin{aligned}y &= \dfrac{8}{3}n + \dfrac{7}{3}\\\\n &= \dfrac{8}{3}y + \dfrac{7}{3}\\\\3n &= 8y + 7\\\\3n-7 &= 8y\\\\y&=\dfrac{3}{8}n-\dfrac{7}{8}\\\\g^{-1}(n)&=\dfrac{3}{8}n-\dfrac{7}{8}\end{aligned}\)
Calculate the inverse of g(x):
\(\begin{aligned}y &= 1-2x^3\\\\x &= 1-2y^3\\\\x -1&=-2y^3\\\\2y^3&=1-x\\\\y^3&=\dfrac{1}{2}-\dfrac{1}{2}x\\\\y&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\g^{-1}(x)&=\sqrt[3]{\dfrac{1}{2}-\dfrac{1}{2}x}\\\\\end{aligned}\)
Answer:
1.
If the composition of two functions is the identity function, then the two functions are inverses. In other words, if f(g(x)) = x and g(f(x)) = x, then f and g are inverses.
For\(\bold{g(x) = 4 + \frac{7}{2}x\: and \:f(x) = 5 -\frac{4}{5}x}\), we have:
\(f(g(x)) = 5 - \frac{4}{5}(4 + \frac{7}{2}x)\\ =5 - \frac{4}{5}(\frac{8+7x}{2})\\=5 - \frac{2}{5}(8+7x)\\=\frac{25-16-14x}{5}\\=\frac{9-14x}{5}\)
\(g(f(x)) = 4 + (\frac{7}{5})(5 - \frac{4}{5}x) \\=4 + (\frac{7}{5})(\frac{25-4x}{5})\\=4+ \frac{175-28x}{25}\\=\frac{100+175-28x}{25}\\=\frac{175-28x}{25}\)
As you can see, f(g(x)) does not equal x, and g(f(x)) does not equal x. Therefore, g(x) and f(x) are not inverses.
Sure, here are the inverses of the functions you provided:
2. g(n) = (8/3)n + 7/3
we can swap the roles of x and y and solve for y to find the inverse of g(n). In other words, we can write the equation as y = (8/3)n + 7/3 and solve for n.
y = (8/3)n + 7/3
n =3/8*( y-7/3)
Therefore, the inverse of g(n) is:
\(g^{-1}(n) = \frac{3}{8}(n - \frac{7}{3})=\frac{3}{8}*\frac{3n-7}{3}=\boxed{\frac{3n-7}{8}}\)
3. g(x) = 1 - 2x^3
We can use the method of substitution to find the inverse of g(x). We can substitute y for g(x) and solve for x.
\(y = 1 - 2x^3\\2x^3 = 1 - y\\x = \sqrt[3]{\frac{1 - y}{2}}\)
Therefore, the inverse of g(x) is:
\(g^{-1}(x) =\boxed{ \sqrt[3]{\frac{1 - x}{2}}}\)
LA
KIUNUL
1
1
1
2.49
2.49
8.99
1
ICE TEA
ICE TEA
CHICKEN, SAND
Rib Sauce
French Fries
CHILI CHEESE DOG
Homemade Coleslaw
(NO BREAD)
(< SEE SERVER>>)
Sub Total
6.49
.69
: 21.15
1. You need to pay 6% tax on your subtotal. How much will
you pay in tax?
2. What is your new total?
M

Answers
Answer:
6
Step-by-step explanation:
The Greens bought a condo for $110,000 in 2005. If its value appreciates at 6%
per year, what will the value be in 2012?
Answers
Answer:
Use the A = p(1 + r/100)^t. A is the amount after appreciation, p is the principal or starting value, r is the interest rate, and t is the time in years.
Step-by-step explanation:
Calculate the value of the discriminant. A=3 B=-7 C=9 SOLVE b^2-4ac
Answers
Answer: -59
Step-by-step explanation: https://byjus.com/discriminant-calculator/
Let (-3,-2) be a point on the terminal side of theta. Find the csc(theta)
Answers
The csc(theta) = 1/sin(theta) = 1/(-2/√13) = -√13/2. So, the cosecant of theta is -√13/2.
To find the cosecant (csc) of theta when a point (-3, -2) lies on its terminal side, we need to determine the hypotenuse (r) of the right triangle formed by this point.
Using the Pythagorean theorem, r^2 = (-3)^2 + (-2)^2. So, r^2 = 9 + 4 = 13, and r = √13.
The csc(theta) is the reciprocal of sin(theta). Sin(theta) is calculated as the ratio of the opposite side (y-coordinate) to the hypotenuse, or sin(theta) = -2/√13.
To learn more about : cosecant
https://brainly.com/question/31708994
#SPJ8
I just need 10 and 11. Pleaseeee. Thank you !

Answers
Answer:
10. x ≈ 15,9
11. x ≈ 17,5
Step-by-step explanation:
10. Use the Pythagorean theorem:
\( {x}^{2} = {17}^{2} - {6}^{2} = 289 - 36 = 253\)
\(x > 0\)
\(x = \sqrt{253} ≈15.9\)
11.
\( {x}^{2} = {9}^{2} + {15}^{2} = 81 + 225 = 306\)
\(x > 0\)
\(x = \sqrt{306} ≈17.5\)
What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/IEnaK9Mnw3ftGn7VoWymvKjzqCukNTp6.png)
Answers
The given passage provides a proof that the Separation Axioms follow from the Replacement Schema.
The proof involves introducing a set F and showing that {a: e X : O(x)} is equal to F (X) for every X. Therefore, the conclusion is that the Separation Axioms can be derived from the Replacement Schema.In the given passage, the author presents a proof that demonstrates a relationship between the Separation Axioms and the Replacement Schema.
The proof involves the introduction of a set F and establishes that the set {a: e X : O(x)} is equivalent to F (X) for any given set X. This implies that the conditions of the Separation Axioms can be satisfied by applying the Replacement Schema. Essentially, the author is showing that the Replacement Schema can be used to derive or prove the Separation Axioms. By providing this proof, the passage establishes a connection between these two concepts in set theory.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
Thank you if you help me

Answers
6x10=60
240-60=180
180/10=18