IN DESPERATE NEED OF HELP! PLEASE ANSWER!! Which of the following represents the synthetic division form of the long division problem below? (x^2+9x-2)÷(x-4)

Answers
Answer:its d
Step-by-step explanation:
Related Questions
Bookwork code: A99
The table shows the hair colours of the
students in a sports team.
Hair colour
Black
Blonde
Brown
Frequency
1
< Back
a) What fraction of the students have brown
hair? Give your answer in its simplest form.
b) How many sections on this pie chart
would you shade to show the students with
brown hair?
4
2
Scroll down
Watch video
Answer >
Answers
A fraction of the students who have brown hair is equal to 1/7.
You should shade only one (1) section on the pie chart to show the number of students with brown hair.
What is a pie chart?In Mathematics, a pie chart can be defined as a type of graph that is used for the graphical representation of the proportion relationship between each part or unit to a whole, especially by dividing a circle into various sectors or sections.
Based on the information provided in the table (see attachment), we can logically deduce the following parameters about the various hair color;
Number of brown hair = 1 brown hair.
Number of blonde hair = 4 blonde hair.
Number of black hair = 2 black hair.
Therefore, the total number of hairs is equal to 7 hairs.
For the fraction of students with brown hair, we have;
Fraction = 1/7.
Read more on pie chart here: brainly.com/question/23608372
#SPJ1

Shureka Washburn has scores of 86, 84, 83, and 49 on her algebra tests.
a. Use an inequality to find the scores she must make on the final exam to pass the course with an average of 76 or higher, given that the final exam counts as two tests.
b. Explain the meaning of the answer to part (a).
Answers
The most appropriate choice for average will be given by-
Shureka Washburn must get 78 or higher in her final exam to make her average 76 or higher.
What is average?
In a data set, there are many numbers. Average is the single number which acts as a representative of all the numbers in the data set.
Average is calculated by sum of all observations divided by total number of observations.
Here,
Let the score of Shureka Washburn in her last test be x
Score of Shurek Washburn on first test = 86
Score of Shurek Washburn on second test = 84
Score of Shurek Washburn on third test = 83
Score of Shurek Washburn on fourth test = 49
Total sum of all her scores = 86 + 84 + 83 + 49 + x
= 302 + x
Average = \(\frac{302 + x }{5}\)
By the problem,
\(\frac{302 + x}{5} \geq 76\)
\(302 + x \geq 76\) \(\times 5\)
\(302 + x \geq 380\)
\(x \geq 380 - 302\)
\(x \geq 78\)
Shureka Washburn must get 78 or higher in her final exam to make her average 76 or higher.
To learn more about average, refer to the link:
https://brainly.com/question/20118982
#SPJ9
im not sure how to go about this one. any help is appreciated
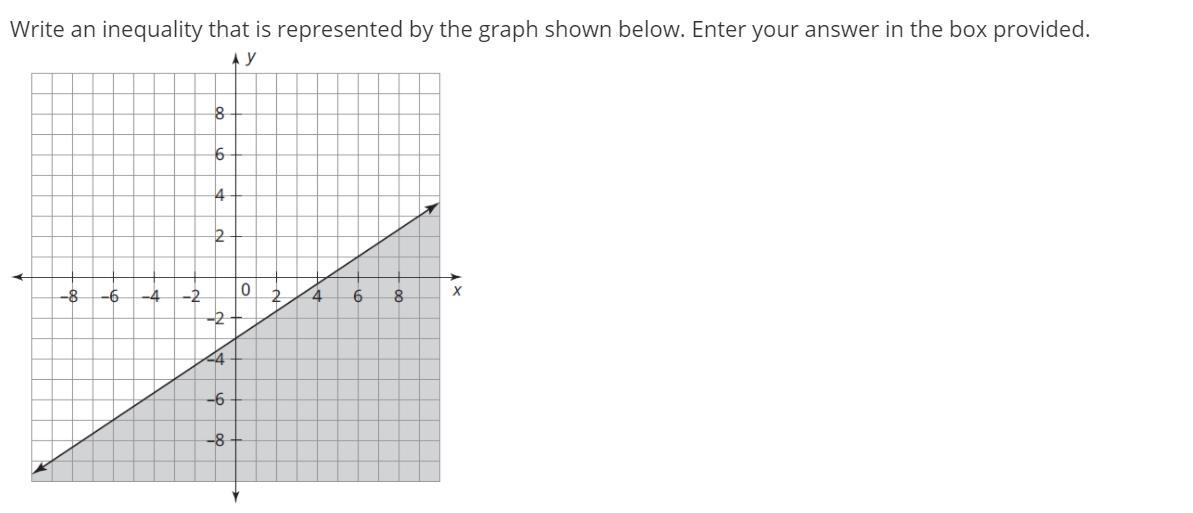
Answers
Answer:
The inequality that represents the graph is:
\(y\leq \frac{2}{3}x+2\)
Step-by-step explanation:
First of all, we need to get the equation of the linear function. We need to choose two points using the graph.
The first point would be (-3,0)
The second point would be (6,1)
The equation of a line is:
\(y=mx+b\)
m is the slope and can be calculated using the points chossen.
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(m=\frac{1+3}{6-0}\)
\(m=\frac{4}{6}\)
\(m=\frac{2}{3}\)
Now, using one point we will find the b value. Let's chose (-3,0)
\(0=m(-3)+b\)
\(0=(\frac{2}{3})(-3)+b\)
\(0=-2+b\)
\(b=2\)
Then, the linear equation is:
\(y=\frac{2}{3}x+2\)
Now, all the allowed values are below the function, therefore the inequality will be:
\(y\leq \frac{2}{3}x+2\)
I hope it helps you!
The length of the line segment
AB equals 3x+1
BC equals 4x-5
AC equals 8x-9
Answers
Answer:
X = 5
Step-by-step explanation:
Here is what I am picturing (not to scale)
A ----------------B-----------C
We are given the information of AB (which equals 3x + 1), BC (which equals 4x - 5), and AC (which equals 8x - 9).
With reference to the line, AB + BC = AC
So,
3x + 1 + 4x - 5 = 8x - 9
7x - 4 = 8x - 9
5 = x
a1=33
an=an–1–7
an=
find the explicit formula
Answers
The explicit formula of the arithmetic sequence in this problem is given as follows:
\(a_n = 40 - 7n\)
What is an arithmetic sequence?An arithmetic sequence is a sequence of values in which the difference between consecutive terms is constant and is called common difference d.
The explicit formula of an arithmetic sequence is given as follows:
\(a_n = a_1 + (n - 1)d\)
From the recursive formula, each term is the previous term subtracted by 7, hence the common difference is given as follows:
d = 7.
The first term of the sequence is given as follows:
\(a_1 = 33\)
Hence the explicit formula is obtained as follows:
\(a_n = a_1 + (n - 1)d\)
\(a_n = 33 - 7(n - 1)\)
\(a_n = 40 - 7n\)
More can be learned about arithmetic sequences at https://brainly.com/question/6561461
#SPJ1
PLEASE HELP A GIRL IN HELPPP

Answers
Answer:
(-25 + 4 squared) x 7
( -25 + 16) x 7
-9 x 7
-63
Step-by-step explanation:
How to do this picture 8th grande math

Answers
Answer:
4.61x10^5
Step-by-step explanation:
You want the first number to be between 0 and 10, not equaling either. So you move the decimal place to the left. Then, you write the second half, which is that you multiply it by ten to the power of however many digits you moved to the left for, which is 5.
Solve x^2-6+58=0 please fast I need help
Answers
Answer:
No real solutions.
Step-by-step explanation:
When solving this equation, you have to figure out if the two sides of an equation equal each other.
Solve.
x^2-6+58 = 0
Answer: No real solutions.
This is due to the fact that x^2-6+58 does not equal 0.
Hope this helps!
Btw, if this is correct, could I have Brainliest? Thanks!
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
The following selected information was extracted from the records of B Solomon.
1. B Solomon, the owner of Solomon Traders, bought a new Machine for R250 000 on 1 July 2013.
2. On 1 October 2014, he purchased a second Machine for R350 000 cash.
3. On 30 June 2015, the Machine bought during 2013 was sold for R120 000 cash.
4. It is the business’ policy to depreciate Machines at 20% per annum on cost.
REQUIRED:
Prepare the following ledger accounts reflecting all applicable entries, in the books of Solomon Traders, properly balanced/closed off, for the years ended 31 March 2016:
1.1. Accumulated depreciation.
1.2. A Machines realisation.
NB: Show all calculations as marks will be awarded for calculations.
Answers
1.1. Accumulated depreciation:
The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.
1.2. Machine realization:
The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.
1.1. Accumulated Depreciation:
To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.
Machine bought on 1 July 2013:
Cost: R250,000
Depreciation rate: 20% per annum on cost
Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000
Accumulated depreciation for the machine bought on 1 July 2013:
As of 31 March 2014: R50,000
As of 31 March 2015: R100,000
As of 31 March 2016: R150,000
1.2. Machine Realisation:
To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.
Machine's original cost: R250,000
Accumulated depreciation as of 30 June 2015: R100,000
Net book value as of 30 June 2015:
R250,000 - R100,000 = R150,000.
On 30 June 2015, the machine was sold for R120,000.
Realisation amount: R120,000
To record the sale:
Debit Cash: R120,000
Debit Accumulated Depreciation: R100,000
Credit Machine: R250,000
Credit Machine Realisation: R120,000
Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).
These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.
For similar question on depreciation.
https://brainly.com/question/15998639
#SPJ8
4. The two legs of a right triangle are equal and the square of its hypotenuse is 50. Find the
length of each leg.
Answers
Answer:
\(Opposite = Adjacent= 5\)
Step-by-step explanation:
Given
\(Hypotenuse^2 = 50\)
\(Opposite = Adjacent\)
Required
Find the length of each leg
This is calculated using Pythagoras Theorem
\(Opposite^2 + Adjacent^2 = Hypotenuse^2\)
\(Opposite^2 + Adjacent^2 = 50\)
Represent the opposite and adjacent with x
\(x^2 + x^2= 50\)
\(2x^2 = 50\)
Divide both sides by 2
\(x^2 = 25\)
Take square roots
\(x = 5\)
Hence:
\(Opposite = Adjacent= 5\)
Suppose IQ scores were obtained for 20 randomly selected sets of couples. The 20 pairs of measurements yield x=97.47​, y=97.35​, r=0.892​, ​P=0.000, and y=-9.15+1.09x​, where x represents the IQ score of the wife. Find the best predicted value of y given that the wife has an IQ of 104​? Use a significance level of 0.05.
Answers
Question:
Suppose IQ scores were obtained for 20 randomly selected sets of couples. The 20 pairs of measurements yield x' =97.47, y' =97.35, r=0.892, P=0.000, and y^=-9.15+1.09x, where x represents the IQ score of the wife. Find the best predicted value of y given that the wife has an IQ of 104? Use a significance level of 0.05.
Answer:
y^ = 104.21
Step-by-step explanation:
Given:
n = 20
x' = 97.47
y' = 97.35
r = 0.892
P-value = 0.000
y^ = -9.15 + 1.09x
Here, the wife has an IQ of 104.
The regression equation here is given as:
y^ = -9.15 + 1.09x
Let x represent the IQ of the wife.
x = 104
Hence, the best predicted value of y^ will be:
Let's substitute 104 for x in tge regression equation.
y^ = -9.15 + 1.09(104)
y^ = - 9.15 + 113.36
y^ = 104.21
Therefore, the best predicted value of y^ = 104.21
can someone help me with this

Answers
The sine equation for the object's height is given as follows:
d = -5sin(0.24t).
How to define the sine function?The standard definition of the sine function is given as follows:
y = Asin(Bx) + C.
The parameters are given as follows:
A: amplitude.B: the period is 2π/B.C: vertical shift.The amplitude for this problem is of 5 inches, hence:
A = 5.
The period is of 1.5 seconds, hence the coefficient B is given as follows:
2π/B = 1.5
B = 1.5/2π
B = 0.24.
The function starts moving down, hence it is negative, so:
d = -5sin(0.24t).
More can be learned about trigonometric functions at brainly.com/question/21558626
#SPJ1
Factor using GCF.
Show your work!
2) 3x^5 - 2x^4 + 5x^2
Answers
If x equals 4hd that means 2^ is not multipication and it is subtracting but we turn that into nagitive and that will turn into a 3 just like mentioned so it is 35
Slope Equations
What is the equation of the line that passes through the point (0,-4) and has a slope of 5?
y = 5x – 4
y= - 4x – 5
y= -5x +4
y=2x - 4
Answers
Linear equations are typically organized in slope-intercept form:
\(y=mx+b\)
m = slopeb = y-intercept (the value of y when x=0)Solving the QuestionWe're given:
m = 5The line passes through the point (0,-4)Because the slope of the line is 5, we know that the m value in y=mx+b has to be 5. This rules out all the options except for the first, which is the only equation in which the m vaue is 5.
On top of that, we know that the y-intercept occurs when x=0. Given that the line passes through the point (0,-4), we know that the y-intercept is -4.
The equation in the first option tells us this as well, as it has -4 as the b value in y=mx+b.
Answery = 5x - 4
Find the value of y.

Answers
The value of y is 4√3
What are similar triangles?Similar triangles have the same corresponding angle measures and proportional side lengths. The corresponding angles of similar triangles are congruent or equal.
Also , the ratio of corresponding sides of similar triangles are equal.
There are two triangles that are similar
Therefore;
y /16 = 4/y
y² = 48
y = √48
y = √16 × √ 3
y = 4√3
Therefore, the value of y is 4√3
learn more about similar triangles from
https://brainly.com/question/14285697
#SPJ1
Evaluate 3x2 + 3x - 9, when x = 2
Answers
3x2 =6 +3(2)-9
= 3
Answer:
9
Step-by-step explanation:
3x^2 + 3x - 9
Substitute x = 2 into the equation.
3(2)^2 + 3(2) - 9
3(4) + 6 - 9
12 + 6 - 9
18 - 9 =
9
(-7x^2+3)-(-4x-3)
(−7x
2
+3)−(−4x−3)
Answers
Answer:
-28x^3-28x^2+16x+15
Step-by-step explanation:-28x^3-28x^2+16x+15
Is −8 a solution to the equation 3x = 16 − 5x? How do you know?
Answers
since the question is saying -8 is the solution, it is saying that -8 = x
if we change x in the equation and put -8, it would end up as -24=56.
in order for the equation to be true, both sides of the equation have to be equal, which in this case it is not
) A watershed experiences a rainfall of 8 inches. What is the runoff volume when the curve number is 80
Answers
Answer:
5.625 inches
Step-by-step explanation:
Given that:
Total Rainfall in inches (P) = 8 inches
The runoff volume (in inches) Q = ???
The curve number CN = 80
Recall that: The runoff volume can be calculated by using the formula:
\(Q = \dfrac{(P-0.2S)^2}{(P+0.8S)}\) for P > 0.2S
Q = 0 for P < 0.2S
\(S = \dfrac{1000}{CN}-10\)
where:
curve number CN = 80
\(S = \dfrac{1000}{80}-10\)
S = 2.5 inches
Since the rainfall (P) is greater than 0.25
Then:
\(Q = \dfrac{(P-0.2S)^2}{(P+0.8S)}\)
\(Q = \dfrac{(8-0.2(2.5))^2}{(8+0.8(2.5))}\)
\(Q = \dfrac{(8-0.5)^2}{(8+2)}\)
\(Q = \dfrac{(7.5)^2}{(10)}\)
\(Q = \dfrac{(56.25)}{(10)}\)
Q = 5.625 inches
Thus, the runoff volume = 5.625 inches
please help me i really need help please

Answers
Answer:
(2,4)
Step-by-step explanation:
A 48-ounce bottle of soda costs $1.79. What is the unit price?
a. $.04
b. $.06
c. $.40
d. $.53
Answers
Answer:
a. $.04
Step-by-step explanation:
$1.79/48 = 0.037 = 0.04
Someone please help me

Answers
Answer:
David had x amount of M&M's. He then ate 15 of them for snack. Now David only has 35 M&M's left. How many M&M's did David have in the beginning?
Step-by-step explanation:
Answer:
X= 20
Step-by-step explanation:
Hannah has 35 marbles. Hannah gives away 15 marbles. How many marbles does Hannah have left? Solve the equation X- 15=35.
Question 13 plz show ALL STEPS so I can learn thnx

Answers
9514 1404 393
Answer:
a) (x³ -x² +x +2) +2/(x+1)
b) (x² +2x -5) +6/(x+3)
Step-by-step explanation:
Polynomial long division is virtually identical to numerical long division, except that the quotient term does not require any guessing. It is simply the ratio of the leading terms of the dividend and divisor. As with numerical long division, the product of the quotient term and the divisor is subtracted from the dividend to form the new dividend for the next step.
The process stops when the dividend is of lower degree than the divisor.
In part (a), you need to make sure the dividend expression has all of the powers of x present. This means terms 0x³ and 0x² must be added as placeholders in the given dividend. They will become important as the work progresses.


Determine the domain and range of the following parabola. f(x)=−3x2−30x−74
Answers
Step-by-step explanation:
1. if to rewrite the given equation, then
y= -3(x+5)²+1;
2. the vertex of the parabola is (-5;1) and it is the highest point. Then
3. domain: x is any value, x∈(-∞;+∞);
range: y not greater than 1, y∈(-∞;1].
For the parabola f(x) = -3x² - 30x - 74, the domain is all real numbers (-∞, ∞), and the range is also all real numbers (-∞, ∞).
To determine the domain and range of the given parabola f(x) = -3x² - 30x - 74, we need to understand the behavior of parabolas.
The domain of a function represents all the possible x-values for which the function is defined. In this case, there are no restrictions on the x-values for the given quadratic function. Therefore, the domain is all real numbers, expressed as (-∞, ∞).
The range of a function represents all the possible y-values that the function can produce. For a parabola, if the coefficient of the squared term (in this case, -3) is negative, the parabola opens downward. Since the coefficient is negative, the parabola will have a maximum value. In this example, there is no minimum or maximum specified; thus, the range will also be all real numbers.
To learn more about parabola click on,
https://brainly.com/question/30997281
#SPJ2
A manufacturer has two options for making cube-shaped boxes. The cost is calculated by multiplying the surface area of the box by the cost per square inch of the cardboard. Answer parts a through c below.
Answers
The quadratic functions are: f(x) = 0.03x² for Design A and g(x) = 0.024x² for Design B.
Describe Quadratic functions?A quadratic function is a type of polynomial function of the form f(x) = ax² + bx + c, where a, b, and c are constants and x is the variable. In a quadratic function, the highest power of the variable is 2.
The graph of a quadratic function is a parabola, which is a U-shaped curve that opens either upwards or downwards depending on the sign of the coefficient a. If a > 0, the parabola opens upwards, and if a < 0, the parabola opens downwards. The vertex of the parabola, which is the point where the curve changes direction, is given by the coordinates (-b/2a, f(-b/2a)).
Quadratic functions have a wide range of applications in various fields such as physics, engineering, economics, and finance. For example, they can be used to model the motion of projectiles, the trajectory of a rocket, the shape of a bridge arch, the optimization of business profits, and the behavior of financial markets.
Let's assume that each side of the cube has a length of x inches. Then, the surface area of the cube is 6x² square inches.
a. For Design A with a cost of $0.005 per square inch, the total cardboard cost can be calculated using the quadratic function:
f(x) = 0.005(6x²) = 0.03x²
b. For Design B with a cost of $0.004 per square inch, the total cardboard cost can be calculated using the quadratic function:
g(x) = 0.004(6x²) = 0.024x²
Therefore, the quadratic functions are:
f(x) = 0.03x² for Design A
g(x) = 0.024x² for Design B
To know more about cube visit:
https://brainly.com/question/29023639
#SPJ1
The complete question is:

Given: BC = DA, LCBD = ZADB
Prove: ABCD = ADAB
Statements
Reasons
I need help:(

Answers
Seventy percent of the children went on the excursion. If 27 stayed at school, how many went?
Answers
By using the Unitary Method we get the number of children who went on an excursion was 63. Thus, the total number of children at school is 90.
We are given that,
No. of children who stayed at school is 27,
Also, 70% of the children went on an excursion.
Suppose, the total number of children in percentage is 100%
Out of which 70% went on an excursion
Thus, the children who stayed at school is 100% - 70% = 30%
By using the Unitary method, we can find out the number of 70% of children.
If 30% of the children are 27
Then 70% of the children are = 27 × 100
30
= 63
∴ the total no. of children in the school = 27 + 63
= 90
To learn more about the Unitary method refer to the link below:
https://brainly.com/question/8083231
simplify 3 ( y − 1 + 2 y )
Answers
Answer:
9y - 3
Step-by-step explanation:
3(y - 1 + 2y)
3y - 3 +6y
9y - 3
A class of 28 students shares a set of 168 markers. On a day with 4 students absent, what is the ratio of students to markers in this class?
Answers
Answer:
1:7
Step-by-step explanation:
There was originally 28 students. Since 4 of them are gone. There are 24 students.
the ratio of students to markers is now:
24:168
Now you have to simplify it by finding the lowest common denominator:
24 and 168 both share 1 so:
24/24 = 1, 168/24 = 7
1:7
Therefore, for every student on that day, there is 7 markers
7 markers per student