In ΔXYZ, ∠Y=90° and ∠X=24°. ∠ZWY=81° and XW=7.1. Find the length of WY to the nearest 10th.
Answers
Answer:
0.5
Step-by-step explanation:
delta math
Related Questions
Use cofunctions of complementary angles to complete the relationship. cos (pi/3)=sin() Find the lengths of the missing sides if side a is opposite angle A, side b cos(B) = 4/5, a = 50
Answers
The relationship between cosine and sine of complementary angles allows us to complete the given equation. Using the cofunction identity, we know that the cosine of an angle is equal to the sine of its complementary angle.
If cos(pi/3) = sin(), we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. To find the lengths of the missing sides in a right triangle, we can use the given information about the angle B and side a. Since cos(B) = 4/5, we know that the adjacent side (side b) is 4 units long and the hypotenuse is 5 units long. Using the Pythagorean theorem, we can find the length of the remaining side, which is the opposite side (side a). Given that a = 50, we can solve for the missing side length. In summary, using the cofunction identity, we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. Additionally, using the given information about angle B and side a, we can find the missing side length by using the Pythagorean theorem.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
Let f(x)=x4−24x2. Determine which intervals f(x) is concave up and on which intervals f(x) is concave down. You must justify your answer with calculus to receive any credit.
Answers
The intervals on which the function is concave up and concave down are:Concave up: x < -2 and x > 2Concave down: -2 < x < 2.
The function f(x) = x4 - 24x2 can be represented as f(x) = x2(x2 - 24).
Therefore, we have to determine the interval(s) on which the function is concave up and down.
We do this by finding the second derivative of the function, f''(x) as follows:
f(x) = x4 - 24x2f'(x) = 4x3 - 48xf''(x) = 12x2 - 48
The concavity of the function is determined by the sign of the second derivative, f''(x).
When f''(x) > 0, the function is concave up
When f''(x) < 0, the function is concave down.
At f''(x) = 0, the function changes from concave up to concave down (or vice versa).
Now, to find the intervals on which the function is concave up or down, we set the second derivative, f''(x) to zero and solve for x as follows:
12x2 - 48 = 012(x2 - 4) = 0x2 - 4 = 0x = ±2
Therefore, the critical points are x = -2 and x = 2, which divide the real line into three intervals.
These intervals are:x < -2, -2 < x < 2, x > 2
We now test these intervals with the second derivative test as follows:
For x < -2, choose x = -3
f''(-3) = 12(-3)2 - 48 = 36 > 0
Therefore, the function is concave up on the interval x < -2.
For -2 < x < 2, choose x = 0f''(0) = 12(0)2 - 48 = -48 < 0
Therefore, the function is concave down on the interval -2 < x < 2.
For x > 2, choose x = 3f''(3) = 12(3)2 - 48 = 36 > 0
Therefore, the function is concave up on the interval x > 2.
The intervals on which the function is concave up and concave down are:
Concave up: x < -2 and x > 2Concave down: -2 < x < 2.
Learn more about Concavity:
brainly.com/question/29530632
#SPJ11
Write 23.4571 correct to
b) the nearest 10
Answers
Answer:
20
Step-by-step explanation:
Answer:
23.50
Step-by-step explanation:
23.4571 rounded of to the nearest tenth 23.4+1
Help fast, 4/9 x 2 = 4 x 2/9
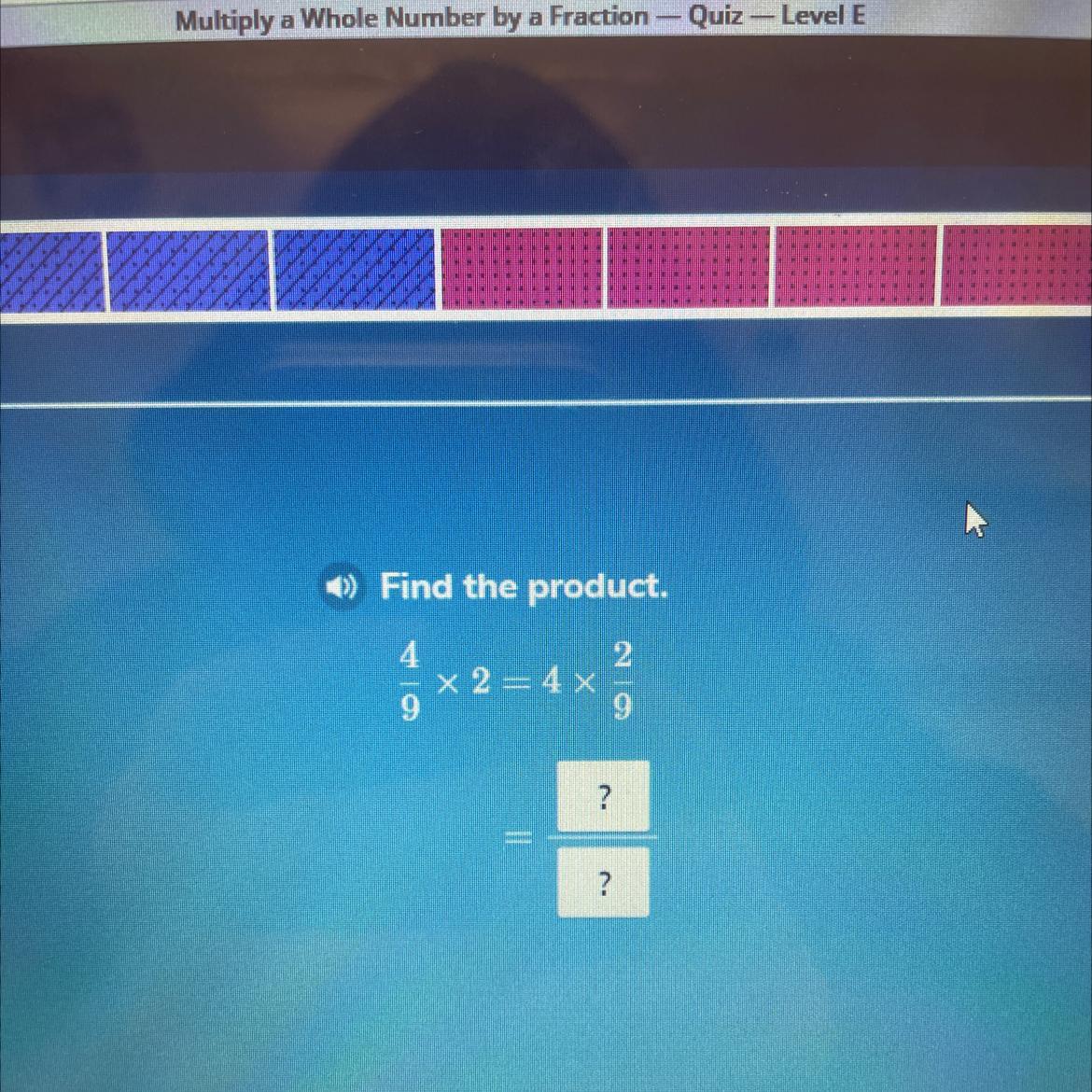
Answers
Answer:
The answer is 8 over 9. 8/9
Answer: 8/9 = 8/9
Step-by-step explanation:
4/9 x 2 = 4 x 2/ 9
= 8/9 = 4x2/9
Multiply:
8/9 = 4x2/9
8/9 = 8/9
What is 10/3(fraction) times 6/5(fraction)
Answers
Answer:
4
Step-by-step explanation:
When multiplying those fractions, you multiply the top (numerators) by each other and you'll get 60
Then when you divide the denominators you'll get 15.
60 divided by 15 is 4.
10/3 x 6/5 = 4
Step-by-step explanation:
You multiply the numerators together, same with the denominator. You get 60/15. You divide those numbers so you get 4 as your answer. Hope this helps!
Curated Practice Problem Set #9
1.
It takes 2 ounces of paint to completely cover all 6 sides of a rectangular prism box which holds 15
cups of sugar. Double the dimensions of the box. Approximately how much paint would the new
box need? How much sugar would it hold?
Answers
As per the given ratio, the amount of paint is 8 ounces needed is and the amount of sugar it will hold 120 ounces.
In math then term ratio is defined as an ordered pair of numbers a and b, written a / b where b does not equal 0
Here we have given that it takes 2 ounces of paint to completely cover all 6 sides of a rectangular prism box which holds 15 cups of sugar.
And then here we have know that they double the dimensions of the box.
Let us consider that the dimension be a.
And as we all know that double the dimensions of the box then dimensions are 2a
Then the ratio of paint and the area of the box remains constant and it can be calculated as,
=> paint / area = 2/x
=> 2/x = 6a² / 6(2a)²
When we simplify this one then we get then x is 8 ounces.
Here we know that the ratio of sugar and the volume of the box remains constant.
Then the sugar volume is calculated as,
=> 15 / X = a³ / (2a)³
When we simplify this then we get the value of x is 120
To know more about ratio here.
https://brainly.com/question/13419413
#SPJ4
Paul had 9.35 ounces of water left in his water jug.
How do you write this number in word form?
Answers
Answer:
Nine and 35 hundredths of water
Step-by-step explanation:
Answer:
9.35 ---> Nine and thirty-five hundredths
Scale the numerator and the denominator down by a factor of 3 (divide) to write a fraction equivalent to \frac{3}{12}
12
3
.
Answers
Answer:
\(\frac{1}{4}\)
Step-by-step explanation:
Given
\(\frac{3}{12}\) ← divide numerator and denominator by 3
= \(\frac{1}{4}\)
I need help with this please

Answers
out of the 100 samples provided by the manufacturer, at most how many can be defective for you to agree to use the new product?
Answers
In order to determine how many defective samples can be acceptable, we need to consider the concept of Acceptable Quality Level (AQL). AQL is the maximum percentage or number of defective units in a batch or lot that can be considered acceptable by the consumer.
AQL is determined based on the criticality of the product and the level of risk that the defects pose to the end user.
The AQL is usually determined through statistical sampling methods. In general, the higher the AQL, the higher the risk that the product may contain defective units. For example, if the AQL is 1%, it means that for every 100 units, one defective unit is acceptable.
In your case, you have not specified the criticality of the product or the level of risk associated with the defects. Therefore, it is difficult to determine the appropriate AQL for your situation. However, assuming a standard AQL of 2.5%, which is commonly used in the industry, it means that out of 100 samples provided by the manufacturer, at most 2.5 units can be defective for you to agree to use the new product.
It is important to note that the AQL is not a guarantee that the product is defect-free. Rather, it is a measure of the acceptable level of defects in a batch or lot. Therefore, it is important to establish appropriate quality control measures to ensure that the product meets the required standards and specifications.
For more questions on consumer
https://brainly.com/question/24553900
#SPJ11
You and your best friend have $10,000 each, which you would like to keep in a savings account. 5/3rd bank offers 4.23% continuous interest and bank of america will give 4.4% interest compounded quarterly. what would be the difference between the two investments after 35yrs? (round to the nearest dollar (whole number))
Answers
The difference between the two investments after 35yrs is $4700 and Bank of America is offering higher interest than 5/3rd banks.
Explain compound interest and continuous interest.Most interest is compounded semiannually, quarterly, or monthly. Continuous compounding assumes that interest is compounded indefinitely and reentered on the balance sheet. The continuous compounding formula takes into account four variables.
For the given question,
5/3rd bank offers continuous interest:
For continuous interest, A = P\(e^{rt}\)
where,
P = the initial amount
A = the final amount
r = the rate of interest
t = time
e is a mathematical constant where e ≈ 2.7183.
A = 10000 × \(2.71^{0.042*35}\)
A = 10000 × 4.04
A = $40400 approximately
Interest = Amount - Principle
Interest = 40400 - 10,000
Interest = $30400
Bank of America offers compound interest:
For compound interest:
\(A = P(1 + \frac{r}{n})^{nt}\)
A = 10000 × 4.51
A = $45100
Interest = Amount - Principle
Interest = 45100 - 10,000
Interest = $35100
The above calculation explains Bank of America is offering higher interest than 5/3rd bank by $35100 - $30400 = $4700
To know more about compound interest and continuous interest visit:
https://brainly.com/question/17185294
#SPJ4
If 72 is added to a number it will be 5 times as larger as it was originally
Answers
Answer:
x=18
Step-by-step explanation:
previous number: x
x+72=5x
72=4x
x=18
Answer: 360
Step-by-step explanation: factor \(2^{3} * 3^{2} * 5\)
What is (-2xy^3z^-2)^3(2x^2y^4z)^-2 simplified?
Answers
Answer: 3 23 divided by 22 = 2(3 - 2) = 21 = 2 think it’s 2
Step-by-step explanation: Changes made to your input should not affect the solution:
(1): "^-2" was replaced by "^(-2)".
(2): "y4" was replaced by "y^4".
STEP
1
:
Equation at the end of step 1
(((0-((2x•(y3))•z))-2)3)•(((2x2•y4)•z)-2)
STEP
2
:
Equation at the end of step
2
:
(((0 - (2xy3 • z)) - 2)3) • (2)(-2)x(-4)y(-8)z(-2)
STEP
3
:
STEP
4
:
Pulling out like terms
4.1 Simplify ( -2xy3z-2 )3
Put the exponent aside and simplfy the base by pulling out like factors :
-2xy3z-2 = -2 • (xy3z+1)
Remember the 4th law of exponents : (a • b)m= am• bm
Retract the exponent and apply the 4th law to the simplified base: ( -2 • (xy3z+1) )3 = (-2)3 • (xy3z+1)3
Trying to factor as a Sum of Cubes:
4.2 Factoring: xy3z+1
Put the exponent aside, try to factor xy3z+1
Theory : A sum of two perfect cubes, a3 + b3 can be factored into :
(a+b) • (a2-ab+b2)
Proof : (a+b) • (a2-ab+b2) =
a3-a2b+ab2+ba2-b2a+b3 =
a3+(a2b-ba2)+(ab2-b2a)+b3=
a3+0+0+b3=
a3+b3
Check : 1 is the cube of 1
Check : x 1 is not a cube !!
Ruling : Binomial can not be factored as the difference of two perfect cubes
Dividing exponents:
4.3 23 divided by 22 = 2(3 - 2) = 21 = 2
Final result :
-2 • (xy3z + 1)3
————————————————
x12y24z6
=
-2y/xz^8
I would show the steps but it’s a lot lol
What is the maximum value of the picture below?

Answers
Answer:
y = 4
Step-by-step explanation:
The maximum value occurs at the vertex
vertex = (2, 4 )
when x = 2 the maximum value is y = 4
Sean buys 7 postcards to send to his friends. He also buys a t-shirt for $15.89 to give to his best friend. He pays a total of $19.32. Write an equation to find how much each postcard costs.
7p + [2] = []
Answers
Let's say that the cost of each postcard is "p".
We can write the equation as follows:
7p + 15.89 = 19.32
If we solve for "p", we get:
7p = 19.32 - 15.89
p = 3.43 / 7
p = $<<3.43/7=0.49>>0.49
Therefore, each postcard costs $0.49.
Explain the procedure for finding the area between two curves. Use one of the following exercises to supplement your answer: 1. F (x)=x2+2x+1 & f(x) = 2x + 5 2. F (y) =y2 & f (y) =y+2
Answers
The procedure for finding the area between two curves Find the intersection points, set up the integral using the difference between the curves, integrate, take the absolute value, and evaluate the result and the area between the two curve in excercise 1 is 40/3
The procedure for finding the area between two curves involves the following steps:
Identify the two curves: Determine the equations of the two curves that enclose the desired area.
Find the points of intersection: Set the two equations equal to each other and solve for the x-values where the curves intersect. These points will define the boundaries of the region.
Determine the limits of integration: Identify the x-values of the intersection points found in step 2. These values will be used as the limits of integration when setting up the definite integral.
Set up the integral: Depending on whether the curves intersect vertically or horizontally, choose the appropriate integration method (vertical slices or horizontal slices). The integral will involve the difference between the equations of the curves.
Integrate and evaluate: Evaluate the integral by integrating the difference between the two equations with respect to the appropriate variable (x or y), using the limits of integration determined in step 3.
Calculate the absolute value: Take the absolute value of the result obtained from the integration to ensure a positive area.
Round or approximate if necessary: Round the final result to the desired level of precision or use numerical methods if an exact solution is not required.
In summary, to find the area between two curves, determine the intersection points, set up the integral using the difference between the curves, integrate, take the absolute value, and evaluate the result.
Here's the procedure explained using the exercises:
Exercise 1:
Consider the functions F(x) = \(x^2 + 2x + 1\)and f(x) = 2x + 5. To find the area between these curves, follow these steps:
Set the two functions equal to each other and solve for x to find the points of intersection:
\(x^2 + 2x + 1 = 2x + 5\)
\(x^2 - 4 = 0\)
(x - 2)(x + 2) = 0
x = -2 and x = 2
The points of intersection, x = -2 and x = 2, give us the bounds for integration.
Now, determine which curve is above the other between these bounds. In this case, f(x) = 2x + 5 is above F(x) =\(x^2 + 2x + 1.\)
Set up the integral to find the area:
Area = ∫[a, b] (f(x) - F(x)) dx
Area = ∫\([-2, 2] ((2x + 5) - (x^2 + 2x + 1)) dx\)
Integrate the expression:
Area = ∫\([-2, 2] (-x^2 + x + 4) dx\)
Evaluate the definite integral to find the area:
Area = \([-x^3/3 + x^2/2 + 4x] [-2, 2]\)
Area = [(8/3 + 4) - (-8/3 + 4)]
Area = (20/3) + (20/3)
Area = 40/3
Therefore, the area between the curves F(x) = \(x^2 + 2x + 1\)and f(x) = 2x + 5 is 40/3 square units.
For more question on integrate visit:
https://brainly.com/question/31415025
#SPJ8
A coin tossed what is the theoretical probability of the coin landing on heads
Answers
Answer: 50%
Step-by-step explanation: each side has a 1 in 2 chance of landing on it
The circle below has center T. Suppose that mUV=68° and that UW is tangent to the circle at U. find the following.(a) m

Answers
Angle UTV is given: 68°
Since the triangle is isoceles, the other two angles measure the same.
This way,
\(\begin{gathered} 68+x+x=180\rightarrow68+2x=180\rightarrow2x=112 \\ \rightarrow x=112 \end{gathered}\)Thereby,
\(m\angle TUV=56\)Notice that
\(m\angle TUV+m\angle\text{VUW}=90\)Because UW is tangent to the circle
Therefore,
\(\begin{gathered} m\angle TUV+m\angle\text{VUW}=90 \\ \rightarrow m\angle\text{VUW}=90-m\angle TUV \\ \rightarrow m\angle\text{VUW}=90-56 \\ \rightarrow m\angle\text{VUW}=34 \end{gathered}\)Answer:
\(\begin{gathered} m\angle UTV=68 \\ m\angle VUW=34 \end{gathered}\)The bottles of soda are sold to the student council in a box weighing 24 pounds. if there are 60 bottles in the box, How much does each bottle of soda weigh
Answers
Answer:
2.5 60÷24=2.5 so there is ur answer hope it helps
Solve each equation m-6=58
M=
Answers
Add 6 to both sides to get m=64
QUESTION 18 If f(x) = |x|2, then f'(0) = 0. O True O False QUESTION 19 The discontinuity of f(x) = O True O False x²-1 x-1 کے at x= 1 is removable.
Answers
Thus, the statement "The discontinuity of f(x) = x²-1 / x-1 at x= 1 is removable" is True.
Answer:
The given functions are f(x) = |x|2 and f(x) = x²-1 / x-1 .
The questions to be answered are: If f(x) = |x|2, then f'(0) = 0. True or False?
The discontinuity of f(x) = x²-1 / x-1 at x= 1 is removable.
True or False?
Solutions:
Let us consider the function f(x) = |x|2
In order to calculate the value of f'(0), we first need to calculate the derivative of the given function.
Let us do that.
f(x) = |x|2
Now, |x| = x, when x ≥ 0 and |x| = -x, when x < 0
Therefore, f(x) = |x|2 = x2,
when x ≥ 0 and f(x) = |x|2 = (-x)2 = x2, when x < 0
The given function is defined for all values of x in the domain and it is differentiable for all x in the domain.
Now, f(x) = x2
Let us find
f'(x)f(x) = x2
Applying the power rule of differentiation, we have
f'(x) = 2xThus, f'(0) = 0×2 = 0
Therefore, f'(0) = 0 is True.
Let us consider the function f(x) = x²-1 / x-1
To check whether the discontinuity of f(x) at x=1 is removable or not, we can check the limit of the function at x=1.
If the limit exists and it is finite, then the discontinuity is removable.
If the limit does not exist or it is infinite, then the discontinuity is not removable.
Now, f(x) = x²-1 / x-1
We can factorize the denominator x-1 and simplify the function
f(x) = x²-1 / x-1 = (x+1)(x-1) / (x-1) = (x+1)
Now, let us find the limit of the function as x approaches 1 from the left-hand side(LHL)
limx→1- f(x) = limx→1- (x+1) = 1+1 = 2
Now, let us find the limit of the function as x approaches 1 from the right-hand side
(RHL)limx→1+ f(x) = limx→1+ (x+1) = 1+1 = 2
Since the LHL and RHL of the function are equal and finite, the limit of the function exists and it is finite.
Therefore, the discontinuity of f(x) at x=1 is removable.
to know more about function discontinuity visit:
https://brainly.com/question/28914808
#SPJ11
Nicholas bought 5 pens for $3. At this rate, how much will he spend on 10 pens?
$10
$6
$5
$3

Answers
The correct answer is $6
How did we figure out this?To solve this question, we need to multiply the numbers given.
Given:
\(10,5,3,2\)
Therefore, the equation goes like this:
\(5*2\\3*2\)
5 x 2 = 103 x 2 = 6Therefore, the correct answer is $6
Let n be the number of trials and p be the probability of success in the binomial distribution. Under which conditions do the Binomial and Poisson distributions give approximate results? n → [infinity], p → 0 n → [infinity], p → 1 n → 0, p → 0 n → 0, p → 1
Answers
Under the Binomial and Poisson distributions gives approximate result is p → 0 n → ∞.
One of the common discrete distribution which is used in Statistics is the Binomial distribution. The Binomial distribution often deals with two types of situations, first, the occurring of an event and second, the non-occurring of an event termed respectively as success and failure. The Binomial distribution can be typically characterized by the two parameters namely “n” and “p” where “n” represents the number of trials and “p” represents the fixed probability of occurring of the desired event.
Further, the Binomial distribution can be visualized as an approach to determine the probability of observing a specified number of successes in a specified number of trials. The typical examples of Binomial distribution in our day-to-day life may include the survival of number of cancer patients, from the treatment offered, over a specified period of time;
Winning the number of seats against the number of candidates filed by a certain political party for an election;
Number of people benefiting from a certain house scheme when applied;
Number of covid patients discharged within three days from the hospital after their admission to a hospital for the treatment.
There is another discrete distribution which is equally popular as the Binomial distribution is the Poisson distribution. While the Binomial distribution deals with the number of trials and the probability of a success, Poisson distribution deals with the average number of successes per day or the number of successes observed per unit of time.
Unlike, in the case of a Binomial distribution, for a Poisson distribution, the knowledge of number of trials to get the observed number of successes is not required. The Poisson distribution has only one parameter namely “m” the mean number of successes per given unit of time.
The Poisson distribution is often taken as a limiting case of Binomial distribution, under the following conditions.
The number of trails is indefinitely large i.e., n → ∞
The probability of success, “p” is very small i.e., p → 0
np is finite i.e., np = m where p = m/n and q = 1 – m/n and m > 0.
However, it is not defined if “n” is large means how large and “p” is closed to zero means how small? It is left to the readers to assume how large n should be and how small p should be? As mentioned earlier, the Poisson distribution is often described as a limiting case of Binomial distribution.
Based on the results of the study , published by me clearly proves that even when 10 ≤ n ≤50 and p ≤ 0.2, the Poisson distribution can be a good approximation to Binomial distribution.
Hence the answer is Under the Binomial and Poisson distributions gives approximate result is p → 0 n → ∞.
To learn more about Binomial and Poisson distributions click here https://brainly.com/question/7283210
#SPJ4
Translate the following C statement into an assembly program, there are three variables x,y and z stored in 32-bit register r1,r2, and r3, respectively. - x=0x000000FF - y=0×000000AB - z=0×000000CD x=x∗y+z−x You are only allowed to use register r0,r1,r2,r3. Hint: Use MLA, to make the code efficient.
Answers
The translation of the C statement into an assembly program using the given registers and the MLA (Multiply Accumulate) instruction.
How to explain the informationMOV r1, #0x000000FF ; Load x into r1
MOV r2, #0x000000AB ; Load y into r2
MOV r3, #0x000000CD ; Load z into r3
MLA r0, r1, r2, r3 ; Multiply r1 (x) by r2 (y), add r3 (z), and store the result in r0
SUB r1, r0, r1 ; Subtract r1 (x) from r0 (result) and store the result in r1
In this code, we first load the values of x, y, and z into registers r1, r2, and r3, respectively. Then, we use the MLA instruction to multiply the values of x and y and add the value of z, storing the result in register r0.
Finally, we subtract the initial value of x (stored in r1) from the result (stored in r0) and store the final result back into r1.
Learn more about program on
https://brainly.com/question/26642771
#SPJ4
Reduce the final answer, \(\frac{22+4}{44+16}\)
Answers
Find the length of the hypotenuse of a right triangle whose legs
measure 6 and 5.
Answers
Answer:
c = 7.81 units
Step-by-step explanation:
To find the hypotenuse of a triangle, we can use the Pythagorean Theorem: a² + b² = c²
a and b are the side lengths, and c is the hypotenuse.
Let's plug in what we know.
a² + b² = c²
(6)² + (5)² = c²
Evaluate the exponents.
36 + 25 = c²
Add.
61 = c²
Take the square root of both sides.
√61 = √c²
7.81 = c
This is your answer.
Hope this helps!
What is the algebraic expression represents four times the quantity 22 less than x ?
Answers
Answer:
4x x 22< x
Step-by-step explanation:
No explanation. Straight answer
Develop the B&B tree for each of the following problems. For convenience, always select x₁ as the branching variable at node 0. Maximize z = 3x₁ + 2.8% subject to 2x + 5.x₂ = 18 4.x₁ + 2x₂ = 18 X₁, X₂0 and integer
Answers
To develop the Branch and Bound (B&B) tree for the given problem, follow these steps:
1. Start with the initial B&B tree, where the root node represents the original problem.
2. Choose \($x_1$\) as the branching variable at node 0. Add two child nodes: one for
\($x_1 \leq \lfloor x_1 \rfloor$ \\(floor of $x_1$) and one for $x_1 \geq \lceil x_1 \rceil$ (ceiling of $x_1$).\)
3. At each node, perform the following steps:
- Solve the relaxed linear programming (LP) problem for the node, ignoring the integer constraints.
- If the LP solution is infeasible or the objective value is lower than the current best solution, prune the node and its subtree.
- If the LP solution is integer, update the current best solution if the objective value is higher.
- If the LP solution is non-integer, choose the fractional variable with the largest absolute difference from its rounded value as the branching variable.
4. Repeat steps 2 and 3 for each unpruned node until all nodes have been processed.
5. The node with the highest objective value among the integer feasible solutions is the optimal solution.
6. Optionally, backtrace through the tree to retrieve the optimal solution variables.
Note: The specific LP problem and its constraints are missing from the given question, so adapt the steps accordingly.
To know more about Probability visit-
brainly.com/question/31828911
#SPJ11
how to graph y=-2/3x-5
-2x+3y=-15
Answers
By plotting the given points (0,-5) , (1,-17/3 ) for y=-2/3x-5 and the points for-2x+3y=-15 are (0,-5) , (1,-13/3) and (2,-11/3) we get the required graph.
What is linear equation ?
Linear equation can be defined as the equation in which highest degree is one.
Given Equation,
y=-2/3x-5 and -2x+3y=-15
So,
use the slope form is
y= mx+b , where m is slope and b is the y-intercept.
find the valued of m an b using the form y = mx+b
m = -2/3 and b=-5
The slope of line is the value of m and y-intercept the value of b
slope = -2/3
Any line can be graphed using two points. Select two x values, and plug them into the equation to find the corresponding 2y values.
create a table for x and y values.
x y
0 -5
1 -17/3
and soon
Similarly for -2x+3y=-15
x y
0 -5
1 -13/3
2 -11/3
and soon
And Hence plot the points in the graph.
Therefore, By plotting the given points (0,-5) , (1,-17/3 ) for y=-2/3x-5 and the points for-2x+3y=-15 are (0,-5) , (1,-13/3) and (2,-11/3) we get the required graph.
To learn more about Linear equation from the given link.
brainly.com/question/29739212
#SPJ1
PLEASE HELP DUE IN 10 MINS!!
Which of the following statements describes the solution set of -5x < 10?
All real numbers that are negative two or less.
All real numbers that are greater than negative two.
All real numbers that are negative two or greater.
All real numbers that are less than negative two.
Answers
Answer:
Its B
Step-by-step explanation:
The correct statement is "All real numbers that are greater than negative two".
What is inequality?A relationship between two expressions or values that are not equal to each other is called inequality.
Given an inequality, -5x<10
On solving, we get,
x > -2
Which is saying that, solution is all real number that is greater than -2.
Hence, All real numbers that are greater than negative two.
For more references on inequalities, click;
https://brainly.com/question/28823603
#SPJ2