In Exercises 26 and 27 write an equation of the line with the given slope and y-intercept.
26. slope: -7/3 and y-intercept: 0
27. slope: 0 and y intercept: -10
Answers
27. y= -10
Related Questions
Bryleigh needs three dozen brownies for a party. Each brownie costs 35¢. How much will Bryleigh have to pay for the brownies? (hint: think how much is in a dozen first.)
Answers
Bryleigh have to pay 1260 cents because this is the cost of three dozen brownies.
According to the question,
We have the following information:
Bryleigh needs three dozen brownies for a party. Each brownie costs 35¢.
Now, we know that one dozen of a product means that there are 12 products in total.
So, 3 dozens of brownies means that 12*3.
So, we have 36 products in total.
Now, we have cost of 1 brownie as 35 cents.
So, the cost of 36 brownies can be easily found by multiplying the cost of 1 brownie by 36.
1 brownie = 35 cents
Cost of 36 brownies = 36*35 cents
Cost of 36 brownies = 1260 cents
Hence, the cost of three dozen brownies for which Bryleigh have to pay is 1260 cents.
To know more about cost of three dozen brownies here
https://brainly.com/question/12058126
#SPJ1
A pair of angles is supplementary if the sum of their measures is 180 degrees. A pair of angels is complementary if the sum of their measures 90 degrees. the supplement of a given angel is 10 degrees more than twice its complement. Let 90-x equal the degree measure of its complement and 180-x equal the degree measure of its supplement. Write and solve an equation to find the measure of the given angel.
Answers
Answer:
The measure of the complement =
= 80°
The measure of the supplement=
= 170°
Step-by-step explanation:
Let
90-x equal the degree measure of its complement
180-x equal the degree measure of its supplement.
We are told in the question that: the supplement of a given angle is 10 degrees more than twice its complement.
Hence, the Equation is;
(180 - x) = 10° + 2(90 - x)
180 - x = 10 + 180 - 2x
Collect like terms
-x + 2x = 10 + 180 - 180
x = 10°
Hence,
The measure of the complement =
90 - x
= 90 - 10
= 80°
The measure of the supplement=
180 - x
= 180 - 10
= 170°
Marisa has started a company to manufacture earrings. She will make $1.00 profit on each pair
of earrings sold, but expects 1 pair in 30 to be returned for repair, which will cost $45.00. Will
she make a profit with her company? Calculate the expected value.
Answers
Marisa has started a company to manufacture earrings. She will make $1.00 profit on each pair of earrings sold, but expects 1 pair in 30 to be returned for repair, which will cost $45.00. At this, Marisa will not make a profit and the expected loss is $15
How to find if Marisa will make a profitinformation from the question
She will make $1.00 profit on each pair of earrings sold
but expects 1 pair in 30 to be returned for repair, which will cost $45.00
This makes that total revenue
= $1.00 * 30 earrings
= $30
for this 30, it is expected to have a repair that costs $45. the profit remaining is
= $30 - $45
= -$15
this signifies a loss of $15
Learn more about loss at:
https://brainly.com/question/21637154
#SPJ1
the sum of renting bowling shoes for $6 and $3 per game
Answers
b is the number of bowling shoes you rent
Answer:
9
Step-by-step explanation: 6+3=9
The rent is $9
If you take the opposite of the product of 8 and -2, will the answer be less than -5, between -5 and 5 and 10, or greater than 10?
Answers
Answer: Greater than 10.
8x-2=-16 the inverse (opposite) of -16 is 16. 16 is greater than 10.
Consider a population that consists of the 55 students enrolled in a statistics course at a large university. If the university registrar were to compile the grade point averages (GPAs) of all 55 students in the course and compute their average, the result would be a mean GPA of 3. 15. Note that this average is unknown to anyone; to collect the GPA information would violate the confidentiality of the students’ academic records.
Suppose that the professor who teaches the course wants to know the mean GPA of the students enrolled in his course. He selects a sample of students who are in attendance on the third day of class. The GPAs of the students in the sample are:
3. 89 4. 00 3. 85 3. 77 3. 81 3. 43 3. 28 3. 27 3. 56 3. 92
The instructor uses the sample average as an estimate of the mean GPA of his students. The absolute value of the error in the instructor’s estimate is:
a. 0. 53
b. 0. 22
c. 0. 52
d. 0. 14
Answers
The absolute value of the error in the instructor's estimate is 0.644.
To find the absolute value of the error in the instructor's estimate, we need to calculate the difference between the sample mean and the population mean.
Given:
Population mean (μ) = 3.15
Sample mean (\(\bar{X}\)) = (3.89 + 4.00 + 3.85 + 3.77 + 3.81 + 3.43 + 3.28 + 3.27 + 3.56 + 3.92) / 10
= 36.78/10
= 3.678
Absolute value of the error = |\(\bar{X}\) - μ|
|\(\bar{X}\) - μ| = |3.678 - 3.15| = 0.528
Therefore, the absolute value of the error in the instructor's estimate is 0.644.
Learn more about Mean here
https://brainly.com/question/31101410
#SPJ4
Simplify this expression.
–6w + (–8.3) + 1.5+ (–7w)
Answers
The simplified form of the expression -6w + (–8.3) + 1.5+ (–7w) is -13w - 6.8.
What is the simplified form of the expression?Given the expression in the question;
-6w + (–8.3) + 1.5+ (–7w)
To simplify, first remove the parenthesis
Note that;
- × + = -- × - = ++ × + = +-6w + × - 8.3 + 1.5 + × - 7w
-6w - 8.3 + 1.5 - 7w
Next collect and add like terms
-6w - 7w - 8.3 + 1.5
Add -6w and -7w
-13w - 8.3 + 1.5
Add -8.3 and 1.5
-13w - 6.8
Therefore, -13w - 6.8 is the simplified form.
Learn more about expressions here: https://brainly.com/question/28959918
#SPJ1
If i did 69 pushups in 5.17 minutes did I do at least 264 pushups in uner 30 minutes how
Answers
If you did 69 pushups in 5.17 minutes, then the total number of pushups you would have done in under 30 minutes would be more than 264. To explain how this is so, we can use proportions and ratios.
To find out how many pushups you can do in under 30 minutes, we can use ratios. If you divide 30 minutes by 5.17 minutes, you get approximately 5.8. This means that you can do the 69 pushups in 5.17 minutes almost 6 times in under 30 minutes. To get an estimate of the total pushups you can do in under 30 minutes, you can multiply 69 by 6, which gives you 414 pushups. However, this is just an estimate.
To find a more accurate estimate, you can use proportions. If you did 69 pushups in 5.17 minutes, you can find out how many pushups you would have done in 1 minute by dividing 69 by 5.17, which gives you approximately 13.36 pushups per minute. To find out how many pushups you would have done in 30 minutes, you can multiply 13.36 by 30, which gives you 400.8 pushups. Therefore, it can be concluded that you would have done more than 264 pushups in under 30 minutes.
To know more about proportions visit:
https://brainly.com/question/30675490
#SPJ11
If the reserve rate is 8% and a bank receives a deposit of $7000, how much of
the $7000 is the bank free to lend?
A. $6440
B. $1400
C. $5600
D. $560
Answers
The bank can borrow $6440 based on the $7000 deposit.
What is defined as the reserve rate?The reserve ratio is the proportion of a commercial bank's deposits that it has to keep in cash as a safeguard in the event of mass customer withdrawals, as determined by the central bank. The reserve ratio is a crucial monetary policy tool used by the Federal Reserve in the United States to continue increasing the economy's money supply.The following deposit amount: $7000
Because the reserve rate is 8%, the bank will reserve 8% of the 7000. The remaining funds can be lent by the bank.
7000 × (8/100) = amount set aside
= $560
Thus, the reserve deposit is $560.
Amount the bank is willing to lend = 7000 - 560 = $6440
Thus, the bank can lend $6440 based on a deposit of $7000.
To know more about the reserve rate, here
https://brainly.com/question/14636945
#SPJ9
A local car dealership is trying to sell all of the cars that are on the lot. Currently, there are 525 cars on the lot, and the general manager estimates that they will consistently sell 50 cars per week. Estimate how many weeks it will take for the number of cars on the lot to be less than 75. Write an inequality that can be used to find the number of full weeks, , it will take for the number of cars to be less than 75. Since is the number of full or complete weeks, = 1 means at the end of week 1. Write and solve the inequality
Answers
Answer:
525/50=10.5 it will take 10.5 weeks to get rid of every car we however only need to have below 75 so 525/50w<75
Step-by-step explanation:
First you need to divide 525 by 50 to show how many weeks it will take to sell all the cars. And then it should be one less week than the answer you just reacieved.
Convert 6 yards into meters. Round your answer to the nearest tenth.
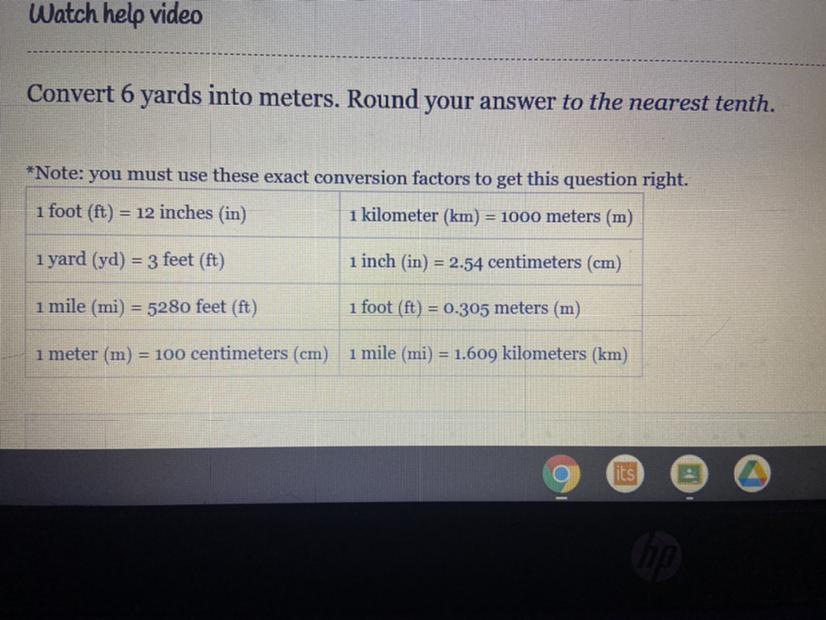
Answers
Answer:
5.4864
Step-by-step explanation:
to the nearest tenth probably 0.5
A company that manufactures light bulbs claims that its light bulbs last an average of 1,150 hours. A sample of 25 light bulbs manufactured by this company gave a mean life of 1,097 hours and a standard deviation of 133 hours. A consumer group wants to test the hypothesis that the mean life of light bulbs produced by this company is less than 1,150 hours. The significance level is 5%. Assume the population is normally distributed. 82. What is the critical value of ? A) -1.704 (B1.711 C) -2.797 D) -2.787
Answers
Calculated t-test statistic (-2.21) is less than the critical value (-1.711), we reject the null hypothesis
The critical value for this hypothesis test can be found using a t-distribution with degrees of freedom (df) equal to the sample size minus one (df = 25-1 = 24) and a significance level of 5%.
Using a t-distribution table or calculator, the critical value for a one-tailed test (since we are testing if the mean is less than 1,150 hours) with 24 degrees of freedom and a 5% significance level is approximately -1.711. Therefore, the answer is B) -1.711.
To conduct the hypothesis test, we would calculate the t-test statistic using the formula:
\(t = (sample mean - hypothesized population mean) / (sample standard deviation / \sqrt{sample size})\)
In this case, the sample mean is 1,097 hours, the hypothesized population mean is 1,150 hours, the sample standard deviation is 133 hours, and the sample size is 25. Plugging these values into the formula, we get:
\(t = (1,097 - 1,150) / (133 / \sqrt{25} )\)= -2.21
Since the calculated t-test statistic (-2.21) is less than the critical value (-1.711), we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that the mean life of light bulbs produced by this company is less than 1,150 hours.
Learn more about hypothesis here:
https://brainly.com/question/29519577
#SPJ11
The 40-hour work week is considered the standard in American society today. Imagine you wish to use data from the 2010 General Social Survey (GSS) to determine whether the mean number of hours worked per week by respondents in the sample differs from the 40- hour standard. a When 81 workers (n) were surveyed how many hours they worked in the previous week, the mean was 44.1 (x-bar) with a standard deviation of 12.8 (sx). Does this suggest that the population mean workweek for workers is different from 40 hours per week? Assume an a = .05. In answering this question, use the six steps below (copy and paste the steps in the space below, and fill in your answers to each question): 1. State the null and research hypotheses 2. State the level of significance, alpha (a) 3. Select a sampling distribution and state the test statistic 4. State the rejection region (critical test statistic) 5. Calculate the research test statistic and see if it falls in the rejection region 6. State your conclusion in terms of the problem
Answers
1. The null hypothesis is H₁: μ = 40 and the alternative hypothesis is H₁: μ ≠ 40
2. The level of significance, alpha (a), is 0.05
3. The test statistic is the z-statistic.
4. The rejection region consists of the values that fall outside the critical test statistic.
5. Tthe z-statistic is 2.88
6. We can reject the null hypothesis.
How to determine if the mean number of hours worked per week differs from the 40-hour standard?We are solving based on the provided steps:
Step 1. State the null and research hypotheses:
Null hypothesis (H0): The population mean workweek for workers is equal to 40 hours per week.Alternative hypothesis (Ha): The population mean workweek for workers is different from 40 hours per week.Step II. State the level of significance, alpha (a):
The level of significance, alpha (a), is 0.05, which relates to a 95% confidence level.
Step III. Select a sampling distribution and state the test statistic:
Since the sample size (n = 81) is greater than 30, we shall use the z-test.
The test statistic is the z-statistic.
Step IV. State the rejection region (critical test statistic):
Since we have a two-tailed test and an alpha level of 0.05, we divide the alpha value equally between the two tails, resulting in an alpha/2 (0.05/2 = 0.025).
To find the critical test statistic, we look up the z-value corresponding to the 0.025 significance level in the standard normal distribution table.
The rejection region consists of the values that fall outside the critical test statistic.
Step V. Then, we calculate the research test statistic to see if it falls in the rejection region:
The formula to calculate the z-statistic is:
z = (x-bar - μ) / (σ / √n)
Where:
x-bar = sample mean μ = population mean σ = population standard deviationn = sample size.Given:
x-bar = 44.1
μ = 40
σ = 12.8
n = 81.
Substitute the values:
z = (44.1 - 40) / (12.8 / √(81))
z = 4.1 / (12.8 / 9)
z = 4.1 / 1.422
z ≈ 2.88
Step VI: State your conclusion in terms of the problem:
After comparing the research test statistic to the critical test statistic from step 5, we find that the z-value of 2.88 falls in the rejection region.
In conclusion, we can reject the null hypothesis.
Hence,
a) Using the sample data from the 2010 GSS, there is evidence to suggest that the population mean workweek for workers is different from 40 hours per week.
b) The research test statistic, with a value of 2.88, falls within the rejection region when compared to the critical test statistic. So, the null hypothesis is rejected.
Learn more about hypothesis at
brainly.com/question/4232174
#SPJ4
Problem 1. Starting at t = = 0, students arrive in Building A according to a Poisson process at rate 4.8 students per minute. Cats enter the building according to a Poisson process of rate one cat per 5 minutes, independently of the student arrival process. (a) Compute the probability that at least one cat has entered the building before the 10th student has. (b) Compute the mean, variance, and the pdf of the time until the third arrival into the building (consid- ering the combined arrivals of students and cats.) (c) Find the probability that among the first 24 arrivals, there is at least one cat. (d) Compute the probability that the 24th arrival is the second cat entering the building. (e) Each cat that enters will leave the building through the other door, after exactly 10 minutes. Compute the expected number of cats in the building at any time, t, as t → [infinity]. (Hint: recall shot noise.)
Answers
The answers are =
a) 0.8647.
b) 25.1302 minutes
c) 0.9990881.
d) 0.0027937.
e) as time approaches infinity, the expected number of cats in the building is 2.
(a) To compute the probability we can use the concept of inter-arrival times in a Poisson process.
The inter-arrival time between student arrivals follows an exponential distribution with a rate of λ = 4.8 students per minute.
Similarly, the inter-arrival time between cat arrivals follows an exponential distribution with a rate of λ' = 1 cat per 5 minutes.
Let T be the time until the 10th student arrives.
The probability that at least one cat has entered before the 10th student is equivalent to the probability that the time until the first cat arrival, denoted by S, is less than T.
The time until the first cat arrival, S, follows an exponential distribution with a rate of λ' = 1 cat per 5 minutes.
To find this probability:
P(S < T) = 1 - exp(-λ'T)
Here, λ'T = 1 × (10/5) = 2, as the time until the 10th student is 10 minutes and the rate for the cat arrival is one cat per 5 minutes.
P(S < T) = 1 - exp(-2) ≈ 0.8647
(b) To compute the mean, variance, and PDF of the time until the third arrival, we need to consider both student and cat arrivals.
Let X be the time until the third arrival.
The time until the third arrival is a random variable composed of the sum of two exponential random variables: the time until the third student, denoted by Xs, and the time until the first cat, denoted by Xc.
The time until the third student, Xs, follows an Erlang distribution with parameters (k = 3, λ = 4.8 students per minute) since we are interested in the third arrival.
The time until the first cat, Xc, follows an exponential distribution with a rate of λ' = 1 cat per 5 minutes.
The mean and variance of Xs can be calculated using the formulas for the Erlang distribution:
Mean of Xs = k/λ = 3/(4.8 students per minute) = 0.625 minutes
Variance of Xs = k/(λ^2) = 3/(4.8^2) = 0.1302 minutes^2
The mean of Xc is given by the inverse of the rate:
Mean of Xc = 1/λ' = 1/(1 cat per 5 minutes) = 5 minutes
Since Xs and Xc are independent, the mean and variance of their sum, X, can be calculated by summing their means and variances:
Mean of X = Mean of Xs + Mean of Xc = 0.625 minutes + 5 minutes = 5.625 minutes
Variance of X = Variance of Xs + Variance of Xc = 0.1302 minutes² + 5 minutes² = 25.1302 minutes²
(c) To find the probability that among the first 24 arrivals there is at least one cat, we can use the complement rule and the fact that the arrivals are independent.
Let A be the event that there is at least one cat among the first 24 arrivals.
The complement of this event, denoted by Ac, is the event that there are no cats among the first 24 arrivals.
The probability of no cats among the first 24 arrivals can be calculated using the Poisson distribution with a rate of λ' = 1 cat per 5 minutes.
We are interested in the probability of no cat arrivals, so we calculate the probability of 0 cat arrivals in 24 inter-arrival times:
P(Ac) = P(0 cats in 24 inter-arrival times) = (exp(-λ' × 5))²⁴ = (exp(-1))²⁴ ≈ 0.0009119
(d) To compute the probability that the 24th arrival is the second cat entering the building, we need to consider the cumulative probability up to the 24th arrival.
Let B be the event that the 24th arrival is the second cat.
The probability of the 24th arrival being the second cat can be calculated using the Poisson distribution with a rate of λ' = 1 cat per 5 minutes. We are interested in the probability of exactly 1 cat arrival in 24 inter-arrival times:
P(B) = P(1 cat in 24 inter-arrival times) = (24 × λ' × 5) × (exp(-λ' × 5))²⁴ = (24 × 1/5) × (exp(-1))²⁴ ≈ 0.0027937
(e) To compute the expected number of cats in the building at any time, t, as t approaches infinity, we can use the concept of shot noise. The shot noise model describes the random process that results from a superposition of random events occurring at different times.
In this case, the arrival of cats can be modeled as a Poisson process with a rate of λ' = 1 cat per 5 minutes.
Each cat stays in the building for exactly 10 minutes and then leaves through the other door.
This means that the arrival and departure processes can be considered as a superposition of Poisson processes.
The expected number of cats in the building at any time, t, as t approaches infinity, is given by the ratio of the arrival rate to the departure rate. In this case, the arrival rate is λ' = 1 cat per 5 minutes, and the departure rate is 1 cat per 10 minutes since each cat stays for 10 minutes.
Expected number of cats = λ' / (1/10) = 1 cat per 5 minutes × 10 minutes = 2 cats
Learn more about Poisson distribution click;
https://brainly.com/question/30388228
#SPJ4
If £1 = US$1.11316 and A$1 = US$0.8558, how many British pounds will you get for one Australian dollar?
=£
Round to two decimal places
Answers
The correct answer is you will get approximately £1.30 for one Australian dollar.
To find out how many British pounds you will get for one Australian dollar, we need to determine the exchange rate between the British pound and the Australian dollar.
Given that £1 = US$1.11316 and A$1 = US$0.8558, we can calculate the exchange rate between the British pound and the Australian dollar as follows:
£1 / (US$1.11316) = A$1 / (US$0.8558)
To find the value of £1 in Australian dollars, we can rearrange the equation:
£1 = (A$1 / (US$0.8558)) * (US$1.11316)
Calculating this expression, we get:
£1 ≈ (1 / 0.8558) * 1.11316 ≈ 1.2992
Therefore, you will get approximately £1.30 for one Australian dollar.
Learn more about statistics here:
https://brainly.com/question/30915447
#SPJ11
what is the range of the possible values of r2? 0 to 1 any positive numerical value -1 to 1 0 to 100
Answers
The range of the possible values of r^2 is 0 to 1. It represents the proportion of the dependent variable’s variance that can be explained by the independent variable(s).
The coefficient of determination, often denoted as r^2, measures the proportion of the dependent variable’s variance that can be explained by the independent variable(s) in a statistical model. The value of r^2 ranges from 0 to 1.
A value of 0 for r^2 indicates that the independent variable(s) does not explain any of the variance in the dependent variable. On the other hand, a value of 1 implies that the independent variable(s) fully explain the observed variance in the dependent variable.
Therefore, the range of the possible values of r^2 is 0 to 1. Any positive numerical value within this range indicates a degree of explanatory power, while values outside this range are not meaningful in the context of r^2. It serves as a useful tool for assessing the strength of a statistical relationship and the predictive ability of a model.
Learn more about Coefficient of determination here: brainly.com/question/29581430
#SPJ11
7.9 , 8.37 , 7.293 , 7.785 , 7.476 greatest to least..pls help!!
Answers
Answer: 7.785,7.476,7.293,8.37.7.9
Step-by-step explanation:
HELPPPPP I NEED HELP ITS URGENT !

Answers
Answer:
-5=m
Step-by-step explanation:
-3/4m-1/2=2+1/4m
-2/4m-1/2=2
-2/4m=2 1/2
m=-5
long division help on 2,3, and 5 they are all lay out how they suppose to i jus need help

Answers
The quotients of the long division expressions are 6x^2 + 2x - 6, 7x^3 - 4x^2 + 6x + 10 and 7x^3 + x^2 - 5x - 8
Evaluating the long division expressionsPolynomial set up 2
The long division expression is represented as
x + 5 | 6x^3 + 32x^2 + 4x - 21
So, we have the following division process
6x^2 + 2x - 6
x + 5 | 6x^3 + 32x^2 + 4x - 21
6x^3 + 30x^2
--------------------------------
2x^2 + 4x - 21
2x^2 + 10x
-------------------------------------
-6x - 21
-6x - 30
------------------------------------------
9
Polynomial set up 3
The long division expression is represented as
2x - 3 | 14x^4 - 29x^3 + 24x^2 + 2x - 29
So, we have the following division process
7x^3 - 4x^2 + 6x + 10
2x - 3 | 14x^4 - 29x^3 + 24x^2 + 2x - 29
14x^4 - 21x^3
--------------------------------
-8x^3 + 24x^2 + 2x - 29
-8x^3 + 12x^2
-------------------------------------
12x^2 + 2x - 29
12x^2 - 18x
------------------------------------------
20x - 29
20x - 30
------------------------------------------
1
Polynomial set up 5
The long division expression is represented as
2x - 1 | 14x^4 - 5x^3 - 11x^2 - 11x + 8
So, we have the following division process
7x^3 + x^2 - 5x - 8
2x - 1 | 14x^4 - 5x^3 - 11x^2 - 11x + 8
14x^4 - 7x^3
--------------------------------
2x^3 - 11x^2 - 11x + 8
2x^3 - x^2
-------------------------------------
-10x^2 - 11x + 8
-10x^2 + 5x
------------------------------------------
-16x + 8
-16x + 8
------------------------------------------
0
Read more about long division at
https://brainly.com/question/30989082
#SPJ1
A department store manager has monitored the number of complaints received per week about poor service. The probabilities for numbers of complaints in a week, established by this review, are shown in the table. Number of complaints 0 1 2 3 4 5 Probability 0.18 0.26 0.35 0.09 0.07 0.05 What is the median of complaints received per week? Please round your answer to the nearest integer. Note that the correct answer will be evaluated based on the full-precision result you would obtain using Excel.
Answers
The median of complaints received per week is 2.
To find the median of complaints received per week, we need to arrange the probabilities in ascending order and then find the probability at the middle position.
Arranging the probabilities in ascending order, we get:
Number of complaints 0 1 2 3 4 5
Probability 0.05 0.07 0.09 0.18 0.26 0.35
The median position is (n+1)/2, where n is the total number of probabilities. In this case, n=6, so the median position is (6+1)/2=3.5.
The probability at position 3 is 0.09 and the probability at position 4 is 0.18. Therefore, the median probability is the average of these two probabilities, which is (0.09+0.18)/2=0.135.
To find the median number of complaints, we need to find the number of complaints that corresponds to the median probability. Starting from the first probability, we add up the probabilities until we reach a total of at least 0.135.
0.05 + 0.07 + 0.09 = 0.21
Therefore, the median number of complaints is 2.
So, the answer is 2 (rounded to the nearest integer).
To learn more about probability visit : https://brainly.com/question/13604758
#SPJ11
The median of complaints received per week is 2.
To find the median of complaints received per week, we need to arrange the probabilities in ascending order and then find the probability at the middle position.
Arranging the probabilities in ascending order, we get:
Number of complaints 0 1 2 3 4 5
Probability 0.05 0.07 0.09 0.18 0.26 0.35
The median position is (n+1)/2, where n is the total number of probabilities. In this case, n=6, so the median position is (6+1)/2=3.5.
The probability at position 3 is 0.09 and the probability at position 4 is 0.18. Therefore, the median probability is the average of these two probabilities, which is (0.09+0.18)/2=0.135.
To find the median number of complaints, we need to find the number of complaints that corresponds to the median probability. Starting from the first probability, we add up the probabilities until we reach a total of at least 0.135.
0.05 + 0.07 + 0.09 = 0.21
Therefore, the median number of complaints is 2.
So, the answer is 2 (rounded to the nearest integer).
To learn more about probability visit : https://brainly.com/question/13604758
#SPJ11
at 2 p.m. the temperature is 18 degrees Fahrenheit at 10 p.m. the temperature is -9 degrees Fahrenheit what is the change in temperature between from 2 to 10 p.m.
Answers
Answer:
:> so sorry Could you help me?
Step-by-step explanation:
Measure the length of a pencil in inches.
Answers
a standard wooden pencil typically measures around 7 inches to 7.5 inches in length.
The average length of a pencil can vary depending on factors such as the type of pencil, region, and manufacturer. However, a standard wooden pencil typically measures around 7 inches to 7.5 inches in length. This range encompasses the most common lengths found in the market.
It's important to note that there may be slight variations in length between different pencil brands and styles. Additionally, specialty or novelty pencils may have different lengths based on their design or intended purpose.
To obtain a more accurate average length for a specific set of pencils or a particular region, you would need to measure a representative sample of pencils and calculate the average length based on the measurements obtained.
Learn more about Measurement here
https://brainly.com/question/28983562
#SPJ4
ellen has a coupon for 1.55 off a loaf of bread. the regular price of the bread is 4.63. the loaf is cut into 14 slices. what is the price per slice if ellen uses her coupon?
Answers
Answer:
$0.22
Step-by-step explanation:
Ellen has a coupon of 1.55 off a loaf of bread
The regular price of the bread is 4.63, the loaf is cut into 14 slices
Therefore if she uses her coupon the price per slice can be calculated as follows
= 4.63-1.55
= 3.08
3.08/14
= 0.22
Hence the price is $0.22
Decompose the figure into regions that are closest to each
vertex. Explain or show your reasoning.
Please fill the blanks in a sentence I need asap !!

Answers
The image is decomposed as follows: H1 and H2. Where original graph is Hx.
Are the images (attached) valid decompositions of the original graph?Yes, they are because, H1 and H1 are both sub-graphs of Hx; alsoH1 ∪ H2 = HxThey have no edges in common.Hence, {H1 , H2} are valid decomposition of G.
What is a Graph Decomposition?A decomposition of a graph Hx is a set of edge-disjoints sub graphs of H, H1, H2, ......Hn, such that UHi = Hx
See the attached for the Image Hx - Pre decomposed and the image after the graph decomposition.
Learn more about decomposition:
https://brainly.com/question/27883280
#SPJ1

Calculate the total surface area and the volume of a cone of base diameter 9cm and slant height of 12cm
Answers
Answer:
T.S.A = 233.29 cm²
volume of the cone = 235.84 cm³
Step-by-step explanation:
Given;
diameter of the cone, d = 9 cm
radius of the cone, r = 4.5 cm
slant height of the cone, l = 12 cm
The total surface of the cone is calculated as;
T.S.A = πr² + πrl
T.S.A = πr(r + l)
T.S.A = 3.142 x 4.5(4.5 + 12)
T.S.A = 233.29 cm²
The volume of the cone is calculated as;
\(V = \frac{1}{3} \pi r^2h\)
Where;
h is height of the cone
h² = 12² - 4.5²
h² = 123.75
h = √123.75
h = 11.12 cm
\(V = \frac{1}{3} \pi \times (4.5)^2 \times 11.12\\\\V = 235.84 \ cm^3\)
You must decide whether to buy new machinery to produce product X or to modify existing machinery. You believe the probability of a prosperous economy next year is 0.7. Prepare a decision tree and use it to calculate the expected value of the buy new option. The payoff table is provided below (+ for profits and - for losses).
When entering the answer, do not use the $ symbol. Do not enter the thousand separator. Enter up to 2 decimal places after the decimal point. For example, $6,525.35 must be entered as 6525.35
N1: Prosperity ($) N2: Recession ($)
A1 (Buy New) $1,035,332 $-150,000
A2(Modify) $823,625 $293,648
Answers
The expected value of the "Buy New" option is 724732.60.
Decision Tree:
To solve the given problem, the first step is to create a decision tree. The decision tree for the given problem is shown below:
Expected Value Calculation: The expected value of the "Buy New" option can be calculated using the following formula:
Expected Value = (Prob. of Prosperity * Payoff for Prosperity) + (Prob. of Recession * Payoff for Recession)
Substituting the given values in the above formula, we get:
Expected Value for "Buy New" = (0.7 * 1,035,332) + (0.3 * -150,000)Expected Value for "Buy New" = 724,732.60
Therefore, the expected value of the "Buy New" option is 724,732.60.
Conclusion:
To conclude, the decision tree is an effective tool used in decision making, especially when the consequences of different decisions are unclear. It helps individuals understand the costs and benefits of different choices and decide the best possible action based on their preferences and probabilities.
The expected value of the "Buy New" option is 724,732.60.
For more questions on expected value
https://brainly.com/question/14723169
#SPJ8
help me please I need

Answers
Answer:
I think the answer is A=49
18.4x - 2.1y +9.6 - (-1.2x) + 3.4
Answers
19.6x -2.1y + 13 is a simplified form of the 18.4x - 2.1y +9.6 - (-1.2x) + 3.4 equation.
What is simplification?Simplifying procedures is one way to achieve uniformity in job efforts, expenses, and time. It reduces diversity and variation that is pointless, harmful, or unneeded. Parenthesis, exponents, multiplication, division, addition, and subtraction are all referred to as PEMDAS. The order of the letters in PEMDAS informs you what to calculate first, second, third, and so on, until the computation is finished, given two or more operations in a single statement.
Given expression 18.4x - 2.1y +9.6 - (-1.2x) + 3.4
Simplifying using PEMDAS
=> 18.4x - 2.1y +9.6 - (-1.2x) + 3.4
First, we will open the bracket
=> 18.4x - 2.1y +9.6 + 1.2x + 3.4
Calculating the like terms
=> 19.6x -2.1y + 13
Therefore, a simplified form of the given equation is 19.6x -2.1y + 13.
Learn more about Simplification here:
https://brainly.com/question/28996879
#SPJ1

isaiah is a high school basketball player. in a particular game, he made some free throws (worth one point each) and some two point shots. isaiah scored a total of 12 points and made 4 times as many free throws as two point shots. write a system of equations that could be used to determine the number of free throws isaiah made and the number of two point shots he made. define the variables that you use to write the system.
Answers
The system of linear equations which could be used to determine the number of free throws isaiah made and the number of two point shots he made is;
x + 2y = 12.x = 4y.Which system of.linear equations can be used to determine the number of each kind of shots he made?Let the number of free throws isaiah made be; x.
Let the number of two point shots he made be; y.
On this note, since the individual, isaiah scored a total of 12 points. The algebraic equations which represents the word phrase is;
x + 2y = 12.
Also, it follows from the task content that;
Isaiah made 4 times as many free throws as two point shots. The equation which represents the situation as described is;
x = 4y.
Consequently, the system of linear equations which correctly could be used to determine the number of free throws and two point shots isaiah made is;
x + 2y = 12.x = 4y.Read more on system of linear equations;
https://brainly.com/question/15976480
#SPJ1
Answer:
zczczczczczcz
Step-by-step explanation:
A store owner gathered data for several days about the methods customers used to pay for their purchases. The scatter plot shows the data she gathered and the line of best fit. The equation of the line of best fit is y = 0. 755x + 11. 339. Based on the line of best fit, approximately how many customers are predicted to use a card to pay on a day when 90 customers pay by cash? a. 68 b. 79 c. 92 d. 104.
Answers
According to the line of best fit, 79 consumers are predicted to use their card to pay during a day when 90 customers pay in cash. The correct answer is C.
The answer is 79. This is because the equation of the line of best fit is:
y = 0.755x + 11.339Which is a linear equation that represents the relationship between the number of customers who pay by cash (x) and the number of customers who pay by card (y).
To use this equation to predict the number of customers who pay by card on a day when 90 customers pay by cash, we can substitute x = 90 into the equation:
y = 0.755x + 11.339y = 0.755(90) + 11.339y = 67.95 + 11.339y = 80.284Y = 79.2879.28 ≈ 79, hence the correct answer is C.
Learn more about equivalent equation here: brainly.com/question/2972832
#SPJ4
