in salem, 82% of the households have cable television and internet access and 90% of the houses have cable television. what is the probability that the house has internet access given that it has cable television?
Answers
This is a case of conditional probability because the probability of one event is dependent on the probability that the other has already occured. The formula for finding the probability of A given B is expressed as
P(AIB) = P(A and B)/P(B)
Let A = the event that the households have cable television
Let B = the event that the households have internet access
Thus,
P(A and B) = 82/100 = 0.82
P(A) = 90/100 = 0.9
Thus, the probability that the house has internet access given that it has cable television is
P(BIA) = P(A and B)/P(A) = 0.82/0.9
P(BIA) = 0.91
o
Related Questions
Is that the right answer..?

Answers
9514 1404 393
Answer:
the correct answer is 47
Step-by-step explanation:
You are correct down to the part where you're adding the numbers.
50 -10 +7 = 40 +7 = 47
__
The sign of the 7 is positive. The minus sign only applies to 10.
_____
Additional comment
Here, 50 -10 is an easy sum. Sometimes it is easier to add all the positive numbers, then subtract the sum of the negative numbers. Here, that would look like ...
(50 +7) -(10) = 57 -10 = 47
How much would you have to deposit today to accumulate the same amount of money that $75 monthly payments at a rate of 3.5% compounding monthly for 10 years in an annuity would
earn?
Round to 2 decimal places and do not include the $
symbol.

Answers
Answer:
To calculate how much you would have to deposit today to accumulate the same amount of money that $75 monthly payments at a rate of 3.5% compounding monthly for 10 years in an annuity would earn, we can use the formula for the present value of an annuity due:
PV = PMT × ((1 - (1 + r/n)^(-n×t)) / (r/n)) × (1 + r/n)
where:
- PV is the present value of the annuity due (the amount you would have to deposit today)
- PMT is the monthly payment ($75)
- r is the annual interest rate (3.5%)
- n is the number of times interest is compounded per year (12 for monthly compounding)
- t is the number of years (10)
PV = 75 × ((1 - (1 + 0.035/12)^(-12×10)) / (0.035/12)) × (1 + 0.035/12) = **$7,360.47**
Therefore, you would have to deposit **$7,360.47** today to accumulate the same amount of money that $75 monthly payments at a rate of 3.5% compounding monthly for 10 years in an annuity would earn.
PLEASE HELP ME WILL GIVE BRAINLIEST

Answers
Answer:
Reason 5
Step-by-step explanation:
Reason 1 and 2 are Given
Reason 3 is Reflexive
Reason 4 is Side-Side-Side congruency
Answer:
Reason 5
Step-by-step explanation:
It helps to know what CPCTC means and how it's used.
CPCTC means "corresponding parts of congruent triangles are congruent."
To use it, you must first either prove two triangles to be congruent or be given that two triangles are congruent.
Once you have the congruent triangles, then you state that two corresponding parts of those triangles are congruent, and you use CPCTC as the reason.
In step 4, the triangles are proven congruent by SSS.
Then CPCTC can be used as reason 5 for stating that the corresponding angles A and C are congruent.
find the highest number of student of whom 125 apples, 150 oranges and 225 mangoes can be divided equally
Answers
Answer:
25
Step-by-step explanation:
find the greatest common factor (GCF) of the 3 quantities using prime factorisation.
125 = 5 × 5 × 5
150 = 2 × 3 × 5 × 5
225 = 3 × 3 × 5 × 5
Next, identify those prime factors that the 3 numbers have in common and multiply them.
the common factors are 5 × 5 = 25
then
125 ÷ 25 = 5
150 ÷ 25 = 6
225 ÷ 25 = 9
the 25 students each get 5 apples, 6 oranges and 9 mangoes
If a = -3, find the value of (the 2 on b and c is squared) a) 2a b) a2 c) 3a2
Answers
Answer:
4, -4, 36
Step-by-step explanation:
a) a*2 = -2*-2 = 4
b) a^2 = -2^2 = -4
c) a*3^2= 3*-2^2 = -36
MA.7.DP.1.4
A group of friends has been given $800 to host a party. They must decide how much money
will be spent on food, drinks, paper products, music and decorations.
Part A. As a group, develop two options for the friends to choose from regarding how to
spend their money. Decide how much to spend in each area and create a circle
graph for each option to represent your choices.
Part B. Mikel presented the circle graph below with his recommendations on how to
spend the money. How much did he choose to spend on food and drinks? How
much did he choose to spend on music?
Party Spending Proposal
Mail
17%
Paper Products
Answers
Answer: $130 money did Brenda and Hazel have all together before buying decorations and snacks.
Here, we have,
You want to know Brenda and Hazel's combined money when the ratio of their remaining balances is 1 : 4 after Brenda spent $58 and Hazel spent $37. They had the same amount to start with.
Setup
Let x represent the total amount the two women started with. Then x/2 is the amount each began with, and their fnal balance ratio is ...
(x/2 -58) : (x/2 -37) = 1 : 4
Solution
Cross-multiplying gives ...
4(x/2 -58) = (x/2 -37)
2x -232 = x/2 -37 . . . . . . eliminate parentheses
3/2x = 195 . . . . . . . . . . . . add 232-x/2
x = (2/3)(195) = 130 . . . . . multiply by 2/3
Brenda and Hazel had $130 altogether before their purchases.
Alternate solution
The difference in their spending is $58 -37 = $21.
This is the same as the difference in their final balances.
That difference is 4-1 = 3 "ratio units", so each of those ratio units is $21/3 = $7.
Their ending total is 1+4 = 5 ratio units, or $35.
The total they started with is $58 +37 +35 = $130.
To earn more on addition click:
brainly.com/question/29560851
#SPJ1
complete question:
Brenda and Hazel decide to throw a surprise party for their friend, Aerica. Brenda and Hazel each go to the store with the same amount of money. Brenda spends $58 on decorations, and Hazel spends $37 on snacks. When they leave the store, the ratio of Brenda’s money to Hazel’s money is 1 : 4. How much money did Brenda and Hazel have all together before buying decorations and snacks?
please help thank you..

Answers
Equation of the volume for a pyramid is
V=l•w•h all divided by 3
the l•w is the base, so multiply 10 and 9
you get 90/3
divide and the answer is 30
In the Gaussian integral, how does the left side of this equation equal the right side? An answer would be really appreciated, thank you.

Answers
the left side of this equation equal the right side through the process of completing the square that establishes the equality between the left side and the right side of the Gaussian integral equation.
How do we calculate?
using completing the square method:
Starting with the left side of the equation:
∫\(e^(^-^x^2)\) dx
\(e^(^-^x^2) = (e^(^-x^2/2))^2\)
∫\((e^(^-^x^2/2))^2 dx\)
let u = √(x²/2) = x = √(2u²).
dx = √2u du.
∫ \((e^(^x^2/2))^2 dx\)
= ∫ \((e^(^-2u^2)\)) (√2u du)
The integral of \(e^(-2u^2)\)= √(π/2).
∫ \((e^(-x^2/2))^2\) dx
= ∫ (√2u du) \((e^(-2u^2))\\\)
= √(π/2) ∫ (√2u du)
We substitute back u = √(x²/2), we obtain:
∫ \((e^(-x^2/2))^2\)dx
= √(π/2) (√(x²/2))²
= √(π/2) (x²/2)
= (√π/2) x²
A comparison with the right side of the equation shows that they are are equal.
Learn more about Gaussian integral equation at:
https://brainly.com/question/33550421
#SPJ1
Insurance withholding varies depending on whether an entire family is covered or only the employee is covered. True False
Answers
Answer:
it would True
Step-by-step explanation:
A person invests 4000 dollars in a bank. The bank pays 5.75% interest compounded quarterly. To the nearest tenth of a year, how long must the person leave the money in the bank until it reaches 5900 dollars?
Answers
Answer:
t = 6.8 years
Step-by-step explanation:
The formula for compound interest is
\(A(t)=P(1+r/n)^n^t\), where P is the principal/amount invested, r is the interest rate, n is the number of compound periods per year (4 for quarterly), and t in the time in years.
We know that A = $5900, P = $4000, and r = 0.0575 (we must convert the percentage to a decimal). We must solve for t and round to the nearest tenth:
\(5900=4000(1+0.0575/4)^(^4^t^)\\\\59/40=(1623/1600)^4^t\\\\log(59/40)=log(1623/1600^4^t)\\\\log(59/40)=4t*log(1623/1600)\\\\log(59/40)/log(1623/1600)=4t\\\\1/4(log(59/40)/log(1623/1600))=t\\\\6.80773607=t\\\\6.8=t\)
. If two of the angles in a scalene triangle are 54° and 87°, what is the other angle?
Answers
The answer is:
⇨ x = 39°Work/explanation:
Bear in mind that the sum of all the angles in a triangle is 180°.
Given two angles, we can easily find the third one.
Let's call it x.
Next, we set up an equation:
\(\sf{54+87+x=180}\)
\(\sf{141+x=180}\)
Subtract 141 on each side.
\(\sf{x=180-141}\)
\(\sf{x=39}\)
Hence, the other angle is 39°.
3. A drone takes off from the base of a mountain at a height of 27 ft below sea level. The drone
then flies up 642 ft before landing at the top of the mountain. How tall is the mountain?
Answers
Answer:
669ft high
Step-by-step explanation:
642+27=669ft
The height of the mountain is 669 ft.
What are Arithmetic operations?Arithmetic operations can also be specified by adding, subtracting, dividing, and multiplying built-in functions.
+ Addition operation: Adds values on either side of the operator.
For example 4 + 2 = 6
- Subtraction operation: Subtracts the right-hand operand from the left-hand operand.
For example 4 -2 = 2
A drone takes off from the base of a mountain at a height of 27 ft below sea level.
To determine the height of the mountain.
Using the arithmetic operations of addition and subtraction,
The drone then flies up 642 ft before landing at the top of the mountain.
Assume that distance below sea level is positive,
So the height of the mountain as
⇒ 642 + 27
⇒ 669 ft
Hence, the height of the mountain is 669 ft.
To learn more about Arithmetic operations here:
brainly.com/question/25834626
#SPJ2
Which of the following is an example of a function with a domain (-∞,+) and a range (-∞,+∞)?
Answers
Answer:
Signum function
Step-by-step explanation:
Hope this helps uuuu
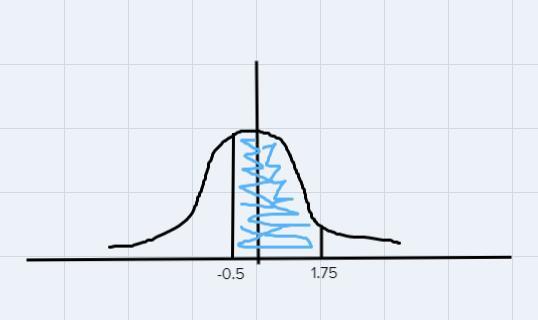
7. Pat and Chris both took a spatial abilities test (mean = 80, std dev. = 8). Pat scores a 76and Chris scored a 94. What proportion of individuals would score between Pat andChris?
Answers
Mean = 80
St Dev = 8
We take this as a normal distribution question.
First, the 68-95-99 rule.
The normal distribution is commonly associated with the 68-95-99 rule.
• 68% of the data is within 1 standard deviation (σ) of the mean (μ),
,• 95% of the data is within 2 standard deviations (σ) of the mean (μ),
,• and 99 of the data is within 3 standard deviations (σ) of the mean (μ).
Checking the two scores, it doesnt fall between any of the rules, so we need to convert to z scores.
The formula is:
\(z=\frac{x-\mu}{\sigma}\)The first score (x) is 76, so corresponding z score is:
\(\begin{gathered} z=\frac{x-\mu}{\sigma} \\ z=\frac{76-80}{8}=-.5 \end{gathered}\)The second score is 94, this corresponds to:
\(z=\frac{94-80}{8}=1.75\)This is:
We want the proportion (percentage).
Which is the blue shaded region.
If we use a normal table, we need:
z(1.75) - z(-0.5)
0.4599+0.1915 = 0.6514
In percentage, that is:
0.6514 * 100 = 65.14%
Hence, 65.14% of individuals would score between Pat and Chris.
2tan(x/2)- csc x=0 interval [0,2pi)
Answers
Answer:
\(x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}\)
Step-by-step explanation:
Given trigonometric equation:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
To solve the equation for x in the given interval [0, 2π), first rewrite the equation in terms of sin x and cos x using the following trigonometric identities:
\(\boxed{\begin{minipage}{4cm}\underline{Trigonometric identities}\\\\$\tan \left(\dfrac{\theta}{2}\right)=\dfrac{1-\cos \theta}{\sin \theta}$\\\\\\$\csc \theta = \dfrac{1}{\sin \theta}$\\ \end{minipage}}\)
Therefore:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
\(\implies 2 \left(\dfrac{1-\cos x}{\sin x}\right)- \dfrac{1}{\sin x}=0\)
\(\implies \dfrac{2(1-\cos x)}{\sin x}- \dfrac{1}{\sin x}=0\)
\(\textsf{Apply the fraction rule:\;\;$\dfrac{a}{c}-\dfrac{b}{c}=\dfrac{a-b}{c}$}\)
\(\dfrac{2(1-\cos x)-1}{\sin x}=0\)
Simplify the numerator:
\(\dfrac{1-2\cos x}{\sin x}=0\)
Multiply both sides of the equation by sin x:
\(1-2 \cos x=0\)
Add 2 cos x to both sides of the equation:
\(1=2\cos x\)
Divide both sides of the equation by 2:
\(\cos x=\dfrac{1}{2}\)
Now solve for x.
From inspection of the attached unit circle, we can see that the values of x for which cos x = 1/2 are π/3 and 5π/3. As the cosine function is a periodic function with a period of 2π:
\(x=\dfrac{\pi}{3} +2n\pi,\; x=\dfrac{5\pi}{3} +2n\pi \qquad \textsf{(where $n$ is an integer)}\)
Therefore, the values of x in the given interval [0, 2π), are:
\(\boxed{x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}}\)

10. Higher Order Thinking Each of 5 friends has x action figures in
his or her collection. Each friend buys 11 more action figures. Now
the 5 friends have a total of 120 action figures.
a. Write an equation that models the problem.
b. Solve the equation to find the number of action figures, x, that
each friend had originally.
Answers
Each friend had originally 13 action figures before buying 11 more.
Given that there are 5 friends and each of them has x action figures in his or her collection. When they buy 11 more action figures, the total number of action figures they will have is 120.
a) We need to find an equation that models the problem. Let x be the original number of action figures that each friend had.
Therefore, the total number of action figures that each friend will have after purchasing 11 more is x + 11.
The total number of action figures will be 5(x + 11) = 5x + 55.
Now, according to the problem,5x + 55 = 120
This is our equation that models the problem.
b) We have to solve the equation 5x + 55 = 120 to find the original number of action figures, x, that each friend had before buying 11 more action figures.
5x + 55 = 120
5x = 120 - 55 (subtract 55 from both sides)
5x = 65x = 13
Therefore, each friend had originally 13 action figures before buying 11 more.
For more such questions on figures, click on:
https://brainly.com/question/24491627
#SPJ8
If Susan will be 2 times old in seven years as she was 3 years ago, what is Susan's present age?
Answers
Answer:
Let's start by assigning a variable to Susan's present age. Let's call it "x".
According to the problem, in seven years, Susan will be "x + 7" years old.
Three years ago, Susan was "x - 3" years old.
The problem tells us that Susan will be 2 times as old in seven years as she was 3 years ago. So we can set up the following equation:
x + 7 = 2(x - 3)
Now we can solve for x:
x + 7 = 2x - 6
x = 13
Therefore, Susan's present age is 13 years old.
Let's assume Susan's present age is "x" years. According to the information provided, "Susan will be 2 times old in seven years as she was 3 years ago."
Seven years from now, Susan's age would be x + 7, and three years ago, her age would have been x - 3. According to the given statement, her age in seven years will be two times her age three years ago:
x + 7 = 2(x - 3)
Let's solve this equation to find Susan's present age:
x + 7 = 2x - 6
Subtracting x from both sides:
7 = x - 6
Adding 6 to both sides:
13 = x
Therefore, Susan's present age is 13 years.
Find the maximum value of the function
f(x) = –22 – 15.9x – 57 to the nearest hundredth.
Answers
find the domain of
f(x)= x-2
——
x^3+x
I already know the answer but I just need to know HOW to get the answer, like steps.

Answers
Answer:
See below.
Step-by-step explanation:
So we have the rational function:
\(f(x)=\frac{x-2}{x^3+x}\)
Now, remember that the domain of rational functions will always be all real numbers... except when the domain is 0.
In other words, to find our domain restrictions, we simply need to solve for the zeros of our denominator.
So, set the denominator to 0 and solve for x:
\(x^3+x=0\)
Factor out an x:
\(x(x^2+1)=0\)
Zero Product Property:
\(x=0\text{ or } x^2+1=0\)
So, our x cannot be 0 according to our first answer.
For the second answer, subtract 1 from both sides:
\(x^2=-1\)
This isn't possible on our coordinate plane. We have no real solution.
Therefore, our only domain restriction is that x cannot be equal to 0.
Therefore, our domain is all real numbers except for x=0.
In set notation, this is:
\(\{x|x\in\mathbb{R},x\neq 0\}\)
And in interval notation, this is:
\((-\infty,0)\cup (0,\infty)\)
Solve the system of equation using elimination

Answers
Answer:
To Solve a System of Equations by Elimination
Write both equations in standard form. ...
Make the coefficients of one variable opposites. ...
Add the equations resulting from Step 2 to eliminate one variable.
Solve for the remaining variable.
Substitute the solution from Step 4 into one of the original equations.
here! ( happy hoildays!)
Allison wants to know how many games teenagers at her school have on their phones. Which answer choice gives an example of a random sample Allsion could use to help answer her question?
A Ask all the 30 female teenagers and 30 male teenagers at the grocery store if they have phones.
B Ask the first 100 people at the library on Saturday morning how many games they have on their phones.
C Ask 10 people from each grade level at Allison's school how many games they have on their phones.
D Ask 5 teenagers from 20 different countries how many games they have on their phones.
Answers
The answer choice which gives the best-example of the "random-sample" is (c) Ask 10 people from each "grade-level" at Allison's school about how many games they have on their phones.
A "Random-Sample" is a subset of a larger population which is chosen in such a way that each member of the population has an equal chance of being selected.
The Option (c) : gives the best example of a random sample that Allison could use to help answer her question. By asking 10 people from each grade level at her school, Allison can obtain a sample that includes a variety of ages, genders, and backgrounds.
This can help to ensure that the sample is representative of the population she is interested in studying.
Option (a) : is not a random sample because it only includes teenagers who happen to be at the grocery store at the time Allison is conducting her survey. This may not represent entire population of teenagers at her school.
Option (b) : is not a random sample either because it only includes people who happen to be at the library on Saturday morning. This may not be representative of the entire population of teenagers at her school.
Option (d) : is not a random sample because it only includes teenagers from 20 different countries. This may not be representative of the population of teenagers at Allison's school or in her local area.
Therefore, the correct option is (c).
Learn more about Random Sample here
https://brainly.com/question/461539
#SPJ1
A (5,3) and B(3,-2) are two fixed points. Find the equation of the locus of P, so that the
area of triangle PAB is 9.
Answers
Answer:
\(37=5x-2y,\,1=5x-2y\)
Step-by-step explanation:
If \((x_1,y_1),\,(x_2,y_2),\,(x_3,y_3)\) are coordinates of a triangle then area of a triangle is equal to \(\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|\)
Let point P be \((x,y)\)
Put \((x_1,y_1)=(5,3),\,(x_2,y_2)=(3,-2),\,(x_3,y_3)=(x,y)\)
Area of a triangle = \(\frac{1}{2}|5(-2-y)+3(y-3)+x(3+2)|\)
\(=\frac{1}{2}|-10-5y+3y-9+5x|\\\\=\frac{1}{2}|-19+5x-2y|\)
Also,
Area of a triangle = 9 square units
\(9=\frac{1}{2}|-19+5x-2y|\\\\18=|-19+5x-2y|\)
±18 = -19 + 5x - 2y
\(18=-19+5x-2y,\,-18=-19+5x-2y\\\\37=5x-2y,\,1=5x-2y\)
• One class is selling tickets for $3.50 each and has already raised $250.
• The other class is selling tickets for $2.25 each and has already raised $300.
How many tickets does each class have to sell so that the total amount raised is the same for both classes?
Answers
Answer:
x=40
Step-by-step explanation:
Carl is making accessories for the soccer team. He uses 773.85 inches of fabric on headbands for 29 players and 4 coaches. He also uses 279.56 inches of fabric on wristbands for just the players. How much fabric was used on a headband and wristband for each player?
Answers
23.45 inches fabric was used on a headband and 9.64 inches fabric was used on a wristband for each player.
No. of players = 29
No. of coaches = 4
Total fabric used for headbands = 773.85 inches
Total no. of people for headbands = 29 + 4
= 33
Fabric used for headband for 1 person = 773.85/33
= 23.45 inches
Total fabric used for wristbands = 279.56 inches
Total no. of people for wristbands = 29
Fabric used for headband for 1 person = 279.56/29
= 9.64 inches
Hence, fabric for headband is 23.45 inches and for wristband is 9.64 inches.
To learn more about fabric here:
https://brainly.com/question/22026300
#SPJ1
Solve the inequality and graph the solution on the line provided. 6x-6<-30
Answers
The solution to the inequality 6x - 6 < -30 is x < -4, and it is graphically represented as a closed circle at -4 and shading to the left of -4 on the number line.
To solve the inequality 6x - 6 < -30, we can follow these steps:
Step 1: Add 6 to both sides of the inequality to isolate the variable:
6x - 6 + 6 < -30 + 6
6x < -24
Step 2: Divide both sides of the inequality by 6 to solve for x:
(6x)/6 < (-24)/6
x < -4
The solution to the inequality is x < -4. This means that any value of x less than -4 will satisfy the inequality.
To graph the solution on the number line, we represent -4 as a closed circle (since it is not included in the solution) and shade the region to the left of -4 to indicate all values less than -4.
On the number line, mark a point at -4 with a closed circle:
<--------●-----------------
Then, shade the region to the left of -4:
<--------●================
The shaded region represents the solution to the inequality x < -4.
For more such question on inequality visit:
https://brainly.com/question/30238989
#SPJ8
write an equation for the graph

Answers
Answer:
y = 2x - 3.
Step-by-step explanation:
The slope is 2 and the y-intercept is at y = -3
2/3+3/4x-1/3=
what is it im confused
Answers
Which of the following best explains why COS 2/3 ≠ cos 5/3

Answers
COS 2/3 ≠ cos 5/3. The reason for this is because the angles themselves are different, resulting in different cosine values when evaluated using the unit circle.
To start, let's first understand what COS represents. COS is an abbreviation for cosine, which is a trigonometric function that represents the ratio of the adjacent side to the hypotenuse in a right triangle.
Now, let's examine the given values, 2/3 and 5/3. These values represent the angles in radians. In trigonometry, an angle is typically measured in radians, not degrees.
In the case of COS 2/3, it means we are considering an angle of 2/3 radians. Similarly, COS 5/3 represents an angle of 5/3 radians.
To determine if COS 2/3 is equal to cos 5/3, we need to evaluate the cosine of each angle.
By using the unit circle, we can find the cosine values for each angle. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane.
When we evaluate the cosine of 2/3 radians on the unit circle, we find a specific point on the circle that corresponds to the cosine value. Similarly, for 5/3 radians, we find another point on the unit circle that corresponds to the cosine value.
Since these two points are different on the unit circle, it means that the cosine values for 2/3 and 5/3 radians are not equal.
For more such questions on angles
https://brainly.com/question/26355390
#SPJ8
Find two positive numbers whose sum is 110 and whose product is a maximum.
Answers
The two positive numbers are 55, and 55.
Given that,
Two positive numbers whose product is a maximum and whose sum is 110.
To Find : Two positive real numbers with a maximum product whose sum is 110.
x + y = 110
x = 110-y
Area = xy = (110-y)y
A = 110y-y^2
Maximum A occurs when y = -b/(2a) = -110/(2*-1) = 55
x + y = 110
x + 55 = 110
x = 55
and y is also 55.
Therefore, the two positive numbers are 55, and 55.
To learn more about Area click here:
brainly.com/question/27683633
#SPJ4
Smaller metric unit to a larger unit:
6,000 grams
kilograms
Answers
6,000 grams is equivalent to 6 kilograms.
How to convert the unitsThe problem is solved by converting the given dimensions from grams to kilograms. The conversion is from a smaller metric unit to a larger metric unit.
A kilogram is a larger unit of measurement for mass or weight compared to a gram.
The prefix kilo in kilogram means 1000, so one kilogram is equal to 1000 grams.
Therefore, to convert from grams to kilograms, you simply divide the number of grams by 1000.
In this case, 6,000 grams divided by 1000 equals 6 kilograms.
Learn more about conversion of units at:
https://brainly.com/question/29755473
#SPJ1