Is 0 and 1 are prime?
Answers
A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. 0 is not a positive integer and 1 is not greater than 1, so they are not considered a prime number.
What is a prime number?A whole number higher than one that cannot be divided exactly by any other whole number than itself and one is a prime number.
What is whole number?Complete numbers, the range of numbers that includes zero and natural numbers and not a decimal or fraction.
To learn more about prime numbers:
brainly.com/question/9315685
#SPJ4
Related Questions
what is the percent of decrease from 3.2 to 1.2 plz help
Answers
Answer:
62.5%
Step-by-step explanation:
(1.2 - 3.2) / 3.2 =
- 2 / 3.2 =
- 0.625 =
- 62.5
The minus (-) reflects the decrease.
Answer:
62.5%
Step-by-step explanation:
if 3.2 - 100%
1.2 - x
x= (1.2*100)/3.2
x = 37.5%
Decrease = 100-37.5 = 62.5%
The first week of January, there are 49 dogs and 28 cats in an animal shelter. Throughout the month, the ratio of dogs to cats remains the same. The last week of January, there are 20 cats in the same shelter. How many dogs are there?
Answers
Answer:
35 dogs
Step-by-step explanation:
DOG:CAT = DOG:CAT
49:28 = x:20
7:4 = x:20
x = 35
Reflect ABC across the y-axis.
A (0,2) B (3, -2) C(-3,-2)
Answers
Answer: just graph it on the y-axis
Step-by-step explanation:
Find angle between 0 and 360 degrees which is coterminal to 600degrees
Answers
Step-by-step explanation:
From starting angle....adding 360 degrees is right back to the same angle
so start by SUBTRACTING those 360 degrees
600 - 360 = 240 degrees <==== Done.
A dog chased a cat up a tree. The cat is 14 feet up the tree. If the dog is standing 3 feet from the tree, what is the distance from the cat to the dog?
Answers
The dog is 11 feet away from the car
Answer:
They would be 11 feet apart.
Step-by-step explanation:
Given equation:
14-3
= 11
They would be 11 feet apart.
Please answer quickly!
Find the equation of the line.
Y=__x + __

Answers
Answer:
y = 3x + 3
Step-by-step explanation:
Using slope intercept form: y = mx + b
where m is the slope(rise over run/change in y over change in x), and b is the y intercept(point where x is 0). We can derive the equation by simply using our mathmatical principles of slope and y intercept. Because our y intercept is where x is 0. Our y intercept is 3 since x is 0 when y is 3 because it touches the axis. Since y is 6 when x is one.
y = mx + b
6 = m(1) + 3
-3 -3
_________
3 = m
_________
m = 3
_________
An m of 3 means that you rise 3 every 1 run or 3y every 1x.
Therefore, our equation in slope intercept is:
y = 3x + 3
“Solve the equations”3x*3-9x^2-54x=0
Answers
x = 0
x = −5
Answer:x=6 x=-3
Step-by-step explanation:
3x(x^2-3x-18)=0
(X-6)(x+3)=0
X-6=0. X+3=0
+6=+6. -3=-3
X=6. X= -3
The number 12 is divisible by... select all that apply.
15 points
2
3
4
5
6
9
10
Answers
Answer:
2, 3, 4, 6
Step-by-step explanation:
Answer:
2,3,4,6
Step-by-step explanation
12 divided by 2 is 6
12 divided by 3 is 4
12 divided by 4 is 3
12 divided by 6 is 2
Can someone help me solve this, I don't understand it.

Answers
Step-by-step explanation:
this, I don't understand it.What is the exact value of sin(cos^-1 (√2/2)) + tan^-1 (sin(π/2))

Answers
\(\qquad \qquad \textit{Inverse Trigonometric Identities} \\\\ \begin{array}{cccl} Function&Domain&Range\\[-0.5em] \hrulefill&\hrulefill&\hrulefill\\ y=cos^{-1}(\theta)&-1 ~\le~ \theta ~\le~ 1& 0 ~\le~ y ~\le~ \pi \\\\ y=tan^{-1}(\theta)&-\infty ~\le~ \theta ~\le~ +\infty &-\frac{\pi}{2} ~\le~ y ~\le~ \frac{\pi}{2} \end{array} \\\\[-0.35em] ~\dotfill\)
\(cos^{-1}\left( -\cfrac{\sqrt{2}}{2} \right)\implies \theta \hspace{5em}\stackrel{\textit{so we can say}}{cos(\theta )=-\cfrac{\sqrt{2}}{2}} \\\\\\ \theta =cos^{-1}\left( -\cfrac{\sqrt{2}}{2} \right)\implies \stackrel{ \textit{on the II Quadrant} }{\theta =\cfrac{3\pi }{4}} \\\\[-0.35em] ~\dotfill\\\\ sin\left[ cos^{-1}\left( -\cfrac{\sqrt{2}}{2} \right) \right]\implies sin\left( \cfrac{3\pi }{4} \right)\implies \boxed{\cfrac{\sqrt{2}}{2}}\)
now let's find the angle for the inverse tangent
\(sin\left( \cfrac{\pi }{2} \right)\implies 1\hspace{5em}\stackrel{\textit{so we can say}}{tan^{-1}\left[ sin\left( \frac{\pi }{2} \right) \right]}\implies tan^{-1}(1) \stackrel{ \textit{on the I Quadrant} }{\implies\boxed{\cfrac{\pi }{4}}} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ sin\left[ cos^{-1}\left( -\frac{\sqrt{2}}{2} \right) \right]~~ + ~~tan^{-1}\left[ sin\left( \frac{\pi }{2} \right) \right]\implies \cfrac{\sqrt{2}}{2}~~ + ~~\cfrac{\pi }{4} \implies \boxed{\cfrac{2\sqrt{2}+\pi }{4}}\)
for the sine function we end up in the II Quadrant because the inverse cosine function range is constrained to the I and II Quadrants only, so our angle comes from that range.
Likewise, our angle from the inverse tangent comes from the I Quadrant, because inverse tangent range is only I and IV Quadrants.
True or False: The margin of error is to account for biased sampling methods.
Answers
Answer:
Step-by-step explanation:
tru i took the test
Choose one answer and explain your choice: Suppose A and B are
disjoint events. Are A and B independent
events? i) Yes
ii) No
iii) It depends.
Answers
If A and B are disjoint events, then the probability of A or B is the sum of their individual probabilities. However, this does not necessarily mean that A and B are independent events.
If A and B are independent events, then the probability of both A and B occurring is the product of their individual probabilities. However, if A and B are disjoint, then the probability of both A and B occurring is zero. Therefore, A and B cannot be independent if they are disjoint events.Hence, the correct answer is (ii) No. A and B are disjoint events, which means that they do not have any outcomes in common. If A and B are independent events, then the occurrence of one event will not affect the occurrence of the other event. If A and B are not independent events, then the occurrence of one event will affect the occurrence of the other event.
Since A and B are disjoint events, they cannot be independent events. If A and B are independent events, then they cannot be disjoint events. Hence, the correct answer is (ii) No
To know more about Probability visit-
https://brainly.com/question/31828911
#SPJ11
What do these terms represent? -8,-4, 0, 4, 8, 12
Answers
Answer:
They represent positive and negative numbers.
Step-by-step explanation:
Calculate the pore compressibility Cpp with porosity 0 = 0.2, Young modulus E = 10 GPa, Poisson's ratio v = 0.2. =
Answers
The pore compressibility (Cpp) can be calculated using the given parameters: porosity (0), Young's modulus (E), and Poisson's ratio (v). With a porosity of 0.2, Young's modulus of 10 GPa, and Poisson's ratio of 0.2, we can determine the pore compressibility.
Pore compressibility is a measure of how much a porous material, such as soil or rock, compresses under the application of pressure. It quantifies the change in pore volume with respect to changes in pressure.
Cpp = (1 - φ) / (E * (1 - 2ν))
Given the values:
φ = 0.2 (porosity)
E = 10 GPa (Young's modulus)
ν = 0.2 (Poisson's ratio)
Substituting these values into the formula, we have:
Cpp = (1 - 0.2) / (10 GPa * (1 - 2 * 0.2))
Simplifying the equation, we get:
Cpp = 0.8 / (10 GPa * (1 - 0.4))
= 0.8 / (10 GPa * 0.6)
= 0.8 / 6 GPa
= 0.133 GPa^(-1)
Therefore, the pore compressibility (Cpp) is approximately 0.133 GPa^(-1).
Learn more about Poisson's ratio here:
https://brainly.com/question/31967309
#SPJ11
Solve 4x- 9 = k for x.
A. x= k+ 9
B. X=
K-9
4
C. X=
k+9
4
D. x = 4 + 9

Answers
Answer:
x = (k+9)/4
Step-by-step explanation:
4x - 9 =k
Add 9 to each side
4x-9+9 = k+9
4x = (k+9)
Divide each side by 4
4x/4 = (k+9)/4
x = (k+9)/4
Answer:
The answer is C
Explanation:
you first add 9 to both sides, you equation will then be 4x = k+9
you then divide both sides by for to get rid of the four from the left side, that will leave you with the equation of x = k+9 over 4
Please help need by tomorrow it would be very very very appreciated

Answers
The linear inequality for the graph in this problem is given as follows:
y ≥ 2x/3 + 1.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the intercept.The graph crosses the y-axis at y = 1, hence the intercept b is given as follows:
b = 1.
When x increases by 3, y increases by 2, hence the slope m is given as follows:
m = 2/3.
Then the linear function is given as follows:
y = 2x/3 + 1.
Numbers above the solid line are graphed, hence the inequality is given as follows:
y ≥ 2x/3 + 1.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
how do I find the values of x and y

Answers
From the properties of the shape (parallelogram) we have that the following is true;
\(4y=6y-42\)&
\(6x-12=2x+36\)Now, we solve each expression for y & x respectively, that is:
\(\Rightarrow4y-6y=-42\Rightarrow-2y=-42\)\(\Rightarrow y=21\)&
\(\Rightarrow6x-2x=36+12\Rightarrow4x=48\)\(\Rightarrow x=12\)So, the values of x & y are 12 & 21 respectively.
a plane intersects both nappes of a double-napped cone but does not go through the vertex of the cone. what conic section is formed? what conic section is formed?
Answers
When a plane intersects both nappes of a double-napped cone but does not go through the vertex of the cone, it forms a hyperbola.
A double-napped cone is a three-dimensional object with two identical nappes, or curved surfaces, that meet at a single vertex. The nappes extend infinitely in both directions away from the vertex.
When a plane intersects the double-napped cone, it cuts through both nappes, resulting in a curve that consists of two separate branches. These branches are symmetrical about the plane that contains the axis of the cone.
The resulting curve, known as a hyperbola, has two distinct arms or branches that open up in opposite directions. The hyperbola is characterized by its center, vertices, asymptotes, and foci. The plane intersects the cone at an angle, which determines the shape and orientation of the hyperbola.
Therefore, when a plane intersects both nappes of a double-napped cone but does not go through the vertex, it forms a hyperbola.
To learn more about conic section click on,
https://brainly.com/question/10183810
#SPJ4
In one population, 30% persons had blue-eyed and in second population 20% had the same blue-eye. A random sample of 200 persons is taken from each population independently and calculate the sample proportion for both samples, then find the probability that the difference in sample proportions is less than or equal to 0.02.
Answers
According to the question, the sample proportion for both samples is 0.30 and 0.20. There is a 75.23% probability that the difference in sample proportions between the two populations is less than or equal to 0.02 based on the given samples.
(a) According to the question, the sample proportion for both samples can be calculated as follows:
For the first population:
Sample Proportion 1 = 0.30
For the second population:
Sample Proportion 2 = 0.20
Therefore, the sample proportion for both samples is 0.30 and 0.20.
(b) To find the probability that the difference in sample proportions is less than or equal to 0.02, we need to calculate the z-score and use the standard normal distribution table or a statistical software.
First, we calculate the standard error using the formula mentioned earlier:
\(\text{Standard Error} = \sqrt{\left(\frac{0.30 \cdot (1 - 0.30)}{200}\right) + \left(\frac{0.20 \cdot (1 - 0.20)}{200}\right)}\)
Substituting the values, we get:
Standard Error ≈ 0.0300
Next, we calculate the z-score using the formula:
\(z = \frac{{0.02 - 0}}{{0.0300}}\)
Calculating the z-score, we get:
z ≈ 0.6667
Now, we can use the standard normal distribution table or a statistical software to find the probability corresponding to the z-score. Let's assume the probability is denoted by P(Z ≤ 0.6667).
Using the table or software, we find that P(Z ≤ 0.6667) ≈ 0.7523.
Therefore, the probability that the difference in sample proportions is less than or equal to 0.02 is approximately 0.7523.
In conclusion, there is a 75.23% probability that the difference in sample proportions between the two populations is less than or equal to 0.02 based on the given samples.
To know more about Probability visit-
brainly.com/question/31828911
#SPJ11
Filling swimming pools A hose can fill a swim-
ming pool in 6 hours. Another hose needs 3 more
hours to fill the pool than the two hoses combined.
How long would it take the second hose to fill the
pool
Answers
Answer:
I think it would take it 9 hours
Solve for x. -3 < x - 10
Answers
Answer:
7 < x
Step-by-step explanation:
-3 < x - 10
+10 +10
------------------
7 < x
Answer:
x > 7
Step-by-step explanation:
-3 < x -10
=> x - 10 > -3
=> x > 10 - 3
=> x > 7
f(x) = xe-x ce-x, for what positive value of c does f have an absolute minimum at x = -5?
Answers
The positive value of c that makes the function f(x) = xe^(-x)ce^(-x) have an absolute minimum at x = -5 is approximately 16.05.
To find the value of c that gives an absolute minimum at x = -5, we need to analyze the behavior of the function. First, we differentiate f(x) with respect to x to find the critical points. The derivative of f(x) is f'(x) = -x^2e^(-2x)ce^(-x). Setting f'(x) = 0 and solving for x, we find x = 0 as a critical point.
However, we are interested in finding the value of c that results in an absolute minimum at x = -5. Plugging x = -5 into f(x), we get f(-5) = -5e^(5)c^(-5)e^(5). Since e^5 is positive, to minimize f(-5), c should be as large as possible. Taking the limit as c approaches infinity, we find that f(-5) approaches 0.
Therefore, c should be a large positive value. Calculating the exact value, we find c ≈ 16.05 gives an absolute minimum at x = -5 for the function f(x).
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
Solve it by using Simplex Method or Big M method
Minimize Z subject to = 4x₁ + 2x2, 3x₁ + x₂ ≥ 27, -x₁ - x₂ = 21, x₁ + 2x₂ ≥ 30, x₁ and x₂ unrestricted in sign. X2 X1
Answers
By applying the Simplex Method or Big M Method to the given problem, the optimal solution for minimizing the objective function Z = 4x₁ + 2x₂ subject to the given constraints is obtained. The optimal solution for the given problem is Z = -27, x₁ = 6, and x₂ = 3.
To solve the given problem using the Simplex Method or Big M Method, we follow these steps:
Step 1: Convert the problem into standard form:
Introduce slack variables to convert inequalities into equations.
Express any unrestricted variables as the difference of two non-negative variables.
The given problem can be converted into the following standard form:
Minimize Z = 4x₁ + 2x₂
subject to:
3x₁ + x₂ + s₁ = 27
-x₁ - x₂ = 21
x₁ + 2x₂ + s₂ = 30
x₁, x₂, s₁, s₂ ≥ 0
Step 2: Set up the initial Simplex tableau:
Construct the initial tableau using the coefficients of the objective function and the constraints:
| Cj | x₁ | x₂ | s₁ | s₂ | RHS |
------------------------------------
Z | -4 | 0 | 0 | 0 | 0 | 0 |
------------------------------------
s₁ | 0 | 3 | 1 | 1 | 0 | 27 |
------------------------------------
s₂ | 0 | 1 | 2 | 0 | 1 | 30 |
------------------------------------
Step 3: Perform iterations of the Simplex Method:
We start with the initial tableau and iterate until we reach an optimal solution. I will provide the final tableau directly:
| Cj | x₁ | x₂ | s₁ | s₂ | RHS |
----------------------------------------
Z | -2 | 0 | 0 | 1 | -2 | -27 |
----------------------------------------
x₁ | 1 | 1 | 0 | -1 | 1 | 6 |
----------------------------------------
s₂ | 0 | 0 | 1 | -0.5| 0.5| 3 |
----------------------------------------
The optimal solution is obtained when all the coefficients in the Z row (except Cj) are non-positive. I
n this case, Z = -27, x₁ = 6, and x₂ = 3. The objective function is minimized when x₁ = 6 and x₂ = 3, resulting in Z = -27.
Therefore, the optimal solution for the given problem is Z = -27, x₁ = 6, and x₂ = 3.
Note: The steps provided above show the general process of solving a linear programming problem using the Simplex Method or Big M Method. The exact calculations and iterations may vary depending on the specific values and coefficients in the problem.
To learn more about Simplex Method visit:
brainly.com/question/30970325
#SPJ11
PLEASE THIS IS AN EMERGENCY I NEED HELP QUICK!!!!!
1.Compare the expressions 7 + 3^2-2x5÷4-1x2 and (¾+ ⅛) ÷ ⅛ - 2^2using < , =, > or . Show your work.
Answer:
Answers
The comparison of the expressions is 7 + 3² -2 * 5 ÷ 4 - 1 * 2 > (¾+ ⅛) ÷ ⅛ - 2²
How to compare the expressionsFrom the question, we have the following parameters that can be used in our computation:
7 + 3^2-2x5÷4-1x2 and (¾+ ⅛) ÷ ⅛ - 2^2
Express the exponents properly
This gives
7 + 3² -2 * 5 ÷ 4 - 1 * 2 and (¾+ ⅛) ÷ ⅛ - 2²
Evaluate the exponents
So, we have the following representation
7 + 9 - 2 * 5 ÷ 4 - 1 * 2 and (¾+ ⅛) ÷ ⅛ - 4
Evaluate the expressions in brackets
So, we have the following representation
7 + 9 - 2 * 5 ÷ 4 - 1 * 2 and 7/8 ÷ ⅛ - 4
Solve the products and quotients
7 + 9 - 2.5 - 2 and 7 - 4
So, we have
11.5 and 3
11.5 is greater than 3
So, we have
11.5 > 3
Rewrite as
7 + 3² -2 * 5 ÷ 4 - 1 * 2 > (¾+ ⅛) ÷ ⅛ - 2²
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1
How do you solve this step by step?
-4(2x+5)-3=35
Answers
Answer:
x = -7.25
Step-by-step explanation:
multiply -4 by 2x + 5 = -8x - 20
-8x -20 -3 = 35
-8x - 23 = 35
-8x = 35 + 23
-8x = 58
x = 58 / -8
x = -7.25
Mr. Harris is adding tiles to his patio area. On Monday, he tiled
of his patio, and on Tuesday, he tiled
of the patio area. How
much would he have left to tile on Wednesday?
Answers
Answer:
The Answer is D
Step-by-step explanation:
there u go
Answer:a
Step-by-step explanation:
john has walked 15% of the way home from school. if he has walked 54 yards so far, how far does he walk home from school
Answers
Answer: John walks a total of 360 yards from school.
Step-by-step explanation:
Let's represent the total distance John walks from school as "x".
According to the problem, John has already walked 15% of the way, which can be written as:
0.15x
We also know that he has walked 54 yards so far, which means:
0.15x = 54
To find the total distance John walks from school, we can solve for "x" by dividing both sides of the equation by 0.15:
x = 54 ÷ 0.15
x = 360
Therefore, John walks a total of 360 yards from school.
To know more about total distance refer here
https://brainly.com/question/6516113#
#SPJ11
A shipping container will be used to transport several 120-kilogram crates across the country by rail. The greatest weight that can be loaded into the container is 27500 kilograms. Other shipments weighing 12400 kilograms have already been loaded into the container. Which inequality can be used to determine x, the greatest number of
120-kilogram crates that can be loaded onto the shipping container?
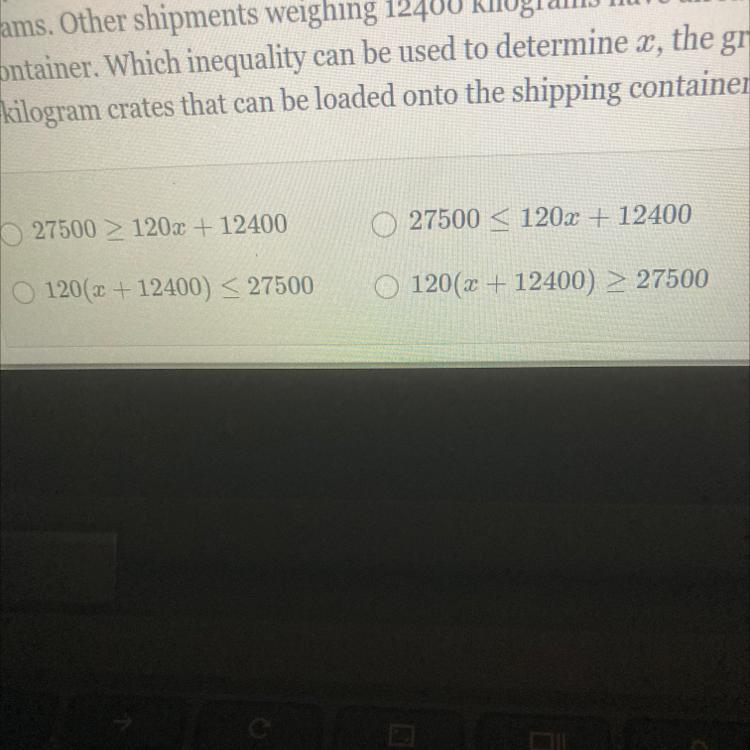
Answers
Inequality can be used to determine x, the greatest number of 120-kilogram crates that can be loaded onto the shipping container is 8000 + 120C <= 27500
What is inequality?An inequality is a relationship that allows us to contrast two or more mathematical expressions.
Knowing that;
Each carton weighs 120 kg.
The container's maximum weight when loaded is 27500 kg.
Weight of the container as it is currently loaded: 8000 kg
Now that we have merged, we have;
Solution
because 8000 grams have already been loaded kilograms
into the container
each crate weighs 120 kilograms.
so 8000 + 120C <= 27500
To learn more about inequality refer to:
https://brainly.com/question/28862943
#SPJ1
Answer these questions

Answers
Answer:
62
8.8
2.7
Step-by-step explanation:
that should be right. try that out
Answer:
62,8.8,2.8
Step-by-step explanation:
Calculate the BMI of an 118-lb adult who is 5 feet 4 inches tall.
Answer:
Logic - BMI formula
703*(lbs/inches^2)
703(118/64^2)=703(118/4096)
703*0.0288=20.2464
Answers
The BMI of an 118-lb adult who is 5 feet 4 inches tall is approximately 20.25.
BMI stands for Body Mass Index.
It's a measure of body fat based on height and weight that applies to both adult men and women.
BMI is an easy-to-perform screening tool for body fat levels that can help identify individuals who have health risks linked with excess body fatness.
It's important to keep in mind that the BMI measurement should not be used as a diagnostic tool for health conditions and is only one component in an overall evaluation of a person's health status.
Using the formula below, we can calculate the BMI of an 118-lb adult who is 5 feet 4 inches tall: BMI = (weight in pounds / (height in inches x height in inches)) x 703
First, we need to convert the height into inches:5 feet 4 inches = 64 inches
Next, we plug the values into the formula and solve for the BMI:
BMI = (118 / (64 x 64)) x 703BMI = (118 / 4,096) x 703BMI = 0.0288 x 703BMI = 20.2464
Therefore, the BMI of an 118-lb adult who is 5 feet 4 inches tall is approximately 20.25.
For more questions on Body Mass Index
https://brainly.com/question/15468401
#SPJ8