Is a parallelogram but not a rectangle
Answers
Answer:
A square
Step-by-step explanation:
A square meets the requirements of a parallelogram.
Related Questions
Please solve this i really need this

Answers
Answer:
a = 8 (to nearest whole number)
Step-by-step explanation:
Given:
m<B = 36°
m<C = 104°
c = 12
Required:
a
SOLUTION:
✔️First find m<A:
m<A = 180 - (104 + 36)
m<A = 40°
✔️Find a using Sine Rule:
Thus:
\( \frac{a}{sin(A)} = \frac{c}{sin(C)} \)
Plug in the values
\( \frac{a}{sin(40)} = \frac{12}{sin(104)} \)
Multiply both sides by sin(40)
\( \frac{a}{sin(40)} * sin(40) = \frac{12}{sin(104)} * sin(40) \)
\( a = \frac{12*sin(40)}{sin(104)} \)
\( a = 8 \) (nearest whole number)
Find the perimeter of a rectangular garden that has a width of 4x−6 and a length of 2x+4.
Answers
Answer:
perimwter = 2(4x-6 + 2x+4) = 2 (6x-2) = 12x-4
(a) The number of terms in an arithmetic progression is 40 and the last is -54. Given that the sum of the 15 terms added to the sum of the first 30 terms is zero. Calculate (1) The first term and common difference, (ii) the sum of the progression.
Answers
(i) The first term (a) is 24 and the common difference (d) is -2.
(ii) The sum of the progression is 2520.
i) Finding the first term and common difference:
Given that the number of terms in the arithmetic progression is 40 and the last term is -54, we can use the formula for the nth term of an arithmetic progression to find the first term (a) and the common difference (d).
The nth term formula is: An = a + (n-1)d
Using the given information, we can substitute the values:
-54 = a + (40-1)d
-54 = a + 39d
We also know that the sum of the first 15 terms added to the sum of the first 30 terms is zero:
S15 + S30 = 0
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values for S15 and S30:
[(15/2)(2a + (15-1)d)] + [(30/2)(2a + (30-1)d)] = 0
Simplifying the equation:
15(2a + 14d) + 30(2a + 29d) = 0
30a + 210d + 60a + 870d = 0
90a + 1080d = 0
a + 12d = 0
a = -12d
Substituting this value into the equation -54 = a + 39d:
-54 = -12d + 39d
-54 = 27d
d = -2
Now we can find the value of a by substituting d = -2 into the equation a = -12d:
a = -12(-2)
a = 24
Therefore, the first term (a) is 24 and the common difference (d) is -2.
ii) Finding the sum of the progression:
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S40 = (40/2)(2(24) + (40-1)(-2))
S40 = 20(48 - 39(-2))
S40 = 20(48 + 78)
S40 = 20(126)
S40 = 2520
Therefore, the sum of the arithmetic progression is 2520.
for such more question on common difference
https://brainly.com/question/25731911
#SPJ8
Please give me the correct answer.

Answers
Answer:
subtract 40 from both sides
Answer:
You subtract 40 which will equal -6 and now you divide -6/4n and the answer is n=-1.5
Step-by-step explanation:
Sheldon needs to buy 8 gallons of ice cream for a family reunion. The table shows the prices for different sizes of two brands of ice cream.
Answers
Answer:
theres no picture so how will we know
Step-by-step explanation:
post the picture first
What is the volume of the pyramid?
A 17cm^3, 56cm^3, 84cm^3 or 168cm^3

Answers
Answer:
56cm2
Step-by-step explanation:
1÷3×4×6×7
=56cm2
The dotplots below display the scores for two classes on a 30-point statistics quiz. Class A has 26 students and Class B has 25 students.
2 dot plots. For Class A, the dots are spread out more. For Class B, the dots are more grouped together.
Which statement best compares the variability of the quiz scores for Class A and Class B?
The scores on the quiz for Class A have more variability than the scores for Class B.
The scores on the quiz for Class B have more variability than the scores for Class A.
The scores on the quiz for Class A have less variability than the scores for Class B.
The scores on the quiz for Class B have about the same variability as the scores for Class A.
I think its (A), The scores on the quiz for Class A have more variability than the scores for Class B. Can someone check me?

Answers
The statement that best compares the variability of the quiz scores for Class A and Class B is A; The scores on the quiz for Class A have more variability than the scores for Class B.
How does the dot plot work?Suppose we're measuring something whose values are numeric. For each value of that thing we observe, we plot a dot above that value in the number line. Thus, the total number of dots in the dot plot tells us the total number of observations of the values of that thing we did.
LEt suppose if we observed the value 'x', then we will make a dot above 'x'. If there is already a dot over 'x', then we will make a new dot over that dot.
The dot plot is skewed to the right due to majority of the data occur to the right of the dot plot.
An outlier is a number that is way smaller or way larger than that of other numbers in a data set. Outliers usually occur with a frequency of one.
For Class A the dots are spread out more.
For Class B, the dots are more grouped together.
Here, Looking at the dot plot, it can be seen that the numbers that range from 16 to 21 have only one dot.
The statement that best compares the variability of the quiz scores for Class A and Class B is A; The scores on the quiz for Class A have more variability than the scores for Class B.
To learn more about outliers, please check: brainly.com/question/27197311
SPJ2
Find the volume of the solid formed by rotating the region inside the first quadrant enclosed by
y=x4 and y=125x
Answers
The volume of the solid formed by rotating the region inside the first quadrant enclosed by y=x⁴ and y=125x is 138438\(\pi\).
Let,
f(x) = 125x
g(x) = x⁴
Intersection points will be,
x⁴ = 125x
x = 0 , 3.3437
Volume V = \(\pi\)\(\int\limits^{3.34}_0{(125x)^{2} - x^8 } \, dx\)
=\(\pi\)\(\int\limits^{3.34}_0 {15625x^2-x^8} \, dx\)
=\(\pi\)[15625x³/3 - x⁹/9]₀³
=\(\pi\)[140625 - 2187]
= 138438\(\pi\)
The volume of the solid formed by rotating the region inside the first quadrant enclosed by two curves can be found using the method of cylindrical shells. This method involves cutting the solid into thin cylindrical shells and finding the volume of each shell. The sum of the volumes of the shells is equal to the volume of the solid.
To learn more about volume of the solid click on,
https://brainly.com/question/22807624
#SPJ4
9^-5*9^-3 Rewrite using a single positive exponent plssss
Answers
Answer:
\(\frac{1}{9^{8}}\)
Step-by-step explanation:
When multiplying two numbers with exponents with the same base, you simply add the two exponents together, even if they're negative:
\(9^{-5}*9^{-3} =9^{-8}\)
When a number has a negative exponent (\(x^{-2}\)) it means that the number is equal to 1/that number (\(\frac{1}{x^{2}}\))
\(9^{-8}=\frac{1}{9^{8}}\)
NEED HELP ASAP WILL MARK BRAINLIEST!
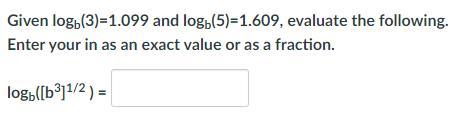
Answers
Answer:
1.5
Explanation:
Given that:
\(\sf log_{b} (3) = 1.099\)\(\sf log_{b} (5) = 1.609\)While solving this problem, the above following is not required to use.
\(\rightarrow \sf log_b ([b^3])^{1/2}\)
apply log rule
\(\rightarrow \sf \dfrac{1}{2}\log _b\left(b^3\right)\)
\(\boxed{\sf \log _b\left(b^3\right)=3}\)
\(\rightarrow \sf \dfrac{1}{2}(3)\)
distribute
\(\rightarrow \sf \dfrac{3}{2} \quad or \quad 1.5\)
Find unit rate $602 for 20 hours of work
Answers
A study of the amount of time it takes a mechanic to rebuild the transmission for a 1992 Chevrolet Cavalier shows that the mean is 8.4 hours and the standard deviation is 1.8 hours. If 40 mechanics are randomly selected, find the probability that their mean rebuild time exceeds 9.1 hours.
A ) 0.1046 B) 0.0069 C ) 0.1285 D ) 0.0046
Answers
Answer:
B) 0.0069
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
\(\mu = 8.4, \sigma = 1.8, n = 40, s = \frac{1.8}{\sqrt{40}} = 0.2846\)
Find the probability that their mean rebuild time exceeds 9.1 hours.
This is 1 subtracted by the pvalue of Z when X = 9.1. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{9.1 - 8.4}{0.2846}\)
\(Z = 2.46\)
\(Z = 2.46\) has a pvalue of 0.9931
1 - 0.9931 = 0.0069
So the answer is B.
Frank ate 12 pieces of pizza and Dave ate 15 pieces. “I ate 1/4 more,” said Dave. “I ate 1/5 less,” said Frank. Who was right?
Answers
Dave and Frank are both right.
The correct answer would be Frank because 12 is less than 15.
What is the fundamental principle of multiplication?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. If an event can occur in m different ways and if following it, a second event can occur in n different ways, then the two events in succession can occur in m × n different ways.
We are given that Frank ate 12 pieces of pizza and Dave ate 15 pieces. “I ate 1/4 more,” said Dave. “I ate 1/5 less,” said Frank.
Therefore, If Dave ate ¼ more than Frank, we would need to divide the denominator by the amount of pizzas,
Thus, if 12÷4 is 3 he ate three more pizzas than Frank.
If we do the same for Frank, ⅕
15÷5=3
Hence, the correct answer would be Frank because 12 is less than 15.
Learn more about multiplications;
https://brainly.com/question/14059007
#SPJ2
solve this equation
3/7x+5=-4/7x-3
Answers
Answer:
x = -8
Step-by-step explanation:
\(\frac{3}{7} x + 5 = \frac{-4}{7} x - 3\\5 = -1x-3\\8 = -1x\\-8 = x\)
if i rolled a dice 50 times and 20 out of the fifity times I got 5 what would the percent be
Answers
Answer:
The percent would be 10 Im guessing
Step-by-step explanation:
Hope this helped :)
You currently have a balance of $34 in your checking account. You then write a check for $76 dollars to pay for groceries. Finally, you deposit a check for $30.
What is your new balance?
Answers
Answer:
Correct me if I'm wrong but I'm sure it's -12
Step-by-step explanation:
34+30= 64
64-76= -12
QUESTION 3
If y varies inversely as x, find the inverse variation equation for the situation.
y = 1/8 when x = 40
Answers
\(yx=5\)
Explanation:
If \(y\) varies inversely as \(x\) then
\(y\times x=k\) for some constant \(k\)
Since \(y = \frac{1}{8}\) when \(x=40\)
\(\huge \text(\dfrac{1}{8}\huge \text)\times(40)=k\)
\(\longrightarrow k=5\)
(01.01 LC) Evaluate the expression 3(7 + 4)2 - 14+7
Answers
Suppose that 10 balls are put into 5 boxes, with each ball independently being put in
box with probability (), ∑(i = 1 to 5) () = 1
(a) Find the expected number of boxes that do not have any balls.
(b) Find the expected number of boxes that have exactly 1 balls.
Answers
Answer:
(a) Let X be the number of boxes that do not have any balls. We can calculate the probability that a particular box is empty, which is (1-p)^10, where p is the probability that a ball is put into that box. The expected number of boxes that are empty is then:
E(X) = 5(1-p)^10 (since each box has the same probability of being empty)
Substituting ∑(i = 1 to 5) p = 1, we get p = 1/5. Therefore,
E(X) = 5(1-1/5)^10 = 5(4/5)^10 ≈ 0.328
So, the expected number of boxes that do not have any balls is approximately 0.328.
(b) Let Y be the number of boxes that have exactly one ball. The probability that a particular box has exactly one ball is given by:
P(exactly one ball in a box) = 10p(1-p)^4
where p is the probability that a ball is put into that box. The expected number of boxes that have exactly one ball is then:
E(Y) = 5(10p(1-p)^4)
Substituting p = 1/5, we get:
E(Y) = 5(10/5^5) = 1/25
So, the expected number of boxes that have exactly one ball is 1/25.
The graph of the function f(x) = –(x + 6)(x + 2) is shown below.
On a coordinate plane, a parabola opens down. It goes through (negative 6, 0), has a vertex at (negative 4, 4), and goes through (negative 2, 0).
Which statement about the function is true?
The function is increasing for all real values of x where
x < –4.
The function is increasing for all real values of x where
–6 < x < –2.
The function is decreasing for all real values of x where
x < –6 and where x > –2.
The function is decreasing for all real values of x where
x < –4.

Answers
Answer:
The function is increasing for all real values of x where
–6 < x < –2.
The angle bisector of the angle ABC is BP. If angle ABP is 6nº, what is angle ABC?
Answers
Answer:
k
Step-by-step explanation:
Calculate Santos's monthly Social Security benefit if he delays collecting for 2 years and his original benefit at full retirement age was $1,115.00.
$1,156.90
$1,209.35
$1,293.40
$1,315.50
Answers
c. $1,293.40 is the Santos's monthly Social Security benefit, after delaying collecting for 2 years.
If Santos delays collecting his Social Security benefits for 2 years, he will be eligible for delayed retirement credits. The amount of the increase depends on his birth year and the specific rules in place at the time. As of my knowledge cutoff in September 2021, for individuals born in 1943 or later, the delayed retirement credit is 8% per year for each year of delay beyond full retirement age.
Assuming Santos's original benefit at full retirement age was $1,115.00, we can calculate the increase after a 2-year delay:
Increase = Original Benefit * (Delayed Retirement Credits per year * Number of years of delay)
Increase = $1,115.00 * (0.08 * 2)
Increase = $1,115.00 * 0.16
Increase = $178.40
To calculate Santos's monthly Social Security benefit after the 2-year delay, we add the increase to his original benefit:
New Benefit = Original Benefit + Increase
New Benefit = $1,115.00 + $178.40
New Benefit = $1,293.40
Santos's monthly Social Security benefit, after delaying collecting for 2 years, would be approximately $1,293.40. Therefore, Option c is correct.
The question was incomplete. find the full content below:
Calculate Santos's monthly Social Security benefit if he delays collecting for 2 years and his original benefit at full retirement age was $1,115.00.
a. $1,156.90
b. $1,209.35
c. $1,293.40
d. $1,315.50
Know more about Social Security benefit here:
https://brainly.com/question/29798181
#SPJ8
Analia is a school district manager. Here are some details about two schools in her district for the last school year: School A School B Number of students 3000 30003000 4000 40004000 Number of teachers 190 190190 380 380380 Graduation rate 86 % 86%86, percent 90 % 90%90, percent Budget per student $ 10 , 500 $10,500dollar sign, 10, comma, 500 $ 10 , 000 $10,000dollar sign, 10, comma, 000 % of students in sports club 62 % 62%62, percent 68 % 68%68, percent Number of sports medals won 9 99 7 77 SAT average 1200 12001200 1050 10501050 SAT range (max-min) 900 900900 700 700700 Analia wants to know which school has higher academic achievements relative to the number of teachers per student. 1) Analia thought of two different ways to define this quantity. Identify these two definitions among the following options.
Answers
The two different quantities to measure which school has higher academic performance are :
• Graduation rate / Budget per student
• SAT average / Budget per student
How to calculate the performance?To specify a number that represents academic achievement. We compare the budget per pupil for each school to a related metric or parameter that measures the academic performance of the students in each school.
The following variables could be used to gauge academic achievement:
• Each school's graduation rate.
• Each school's average SAT score.
Therefore, Graduation rate / Budget per student and SAT average / Budget per student are appropriate in this case.
Learn more about ratio on:
https://brainly.com/question/2328454
#SPJ1
Which of the following graphs could be the graph of the function f(x) = x4 + x3 – x2-x?
Answers
Answer:
Therefore, at x=0, -1, 1 , f(x) will be 0 . Hence, 0, -1 ,1 are the x-intercepts.
Plotting the graph on desmos, the graph will be as in the attachme
Step-by-step explanation:
f(x)=x^4+x^3-x^2-x
=x^3(x+1)-x(x+1)
=(x+1)(x^3-x)
=(x+1)x(x^2-1)
=(x+1)x(x+1)(x-1)
=(x+1)2x(x-1)
the temperature is -56F. How many degreees below zero is the temperature?
Answers
The number of degrees below zero is given by A = 56° F
What is Modulus Function?Regardless of the sign, a modulus function returns the magnitude of a number. The absolute value function is another name for it.
It always gives a non-negative value of any number or variable. Modulus function is denoted as y = |x| or f(x) = |x|, where f: R → (0,∞) and x ∈ R.
The value of the modulus function is always non-negative. If f(x) is a modulus function , then we have:
If x is positive, then f(x) = x
If x = 0, then f(x) = 0
If x < 0, then f(x) = -x
Given data ,
Let the initial temperature be represented as T
Let the number of degrees below zero be A
Now , the value of T is
T = -56° F
From the modulus function , we get
The value of the modulus function is always non-negative.
So , the measure of A = | T |
A = | -56 |
A = 56° F
Hence , the number of degrees below zero is 56° F
To learn more about modulus function click :
https://brainly.com/question/13682596
#SPJ9
The graph shows the position (distant from home) of a bicycle rider on a 42-minute trip. Letters A through E are time intervals during the trip. The key defines the length of each interval.
Use the equation below to calculate the bicycle rider’s average speed in kilometers per minute for the first 30 minutes of the trip
Distance(km)/time(min) = average speed

Answers
The average speed on the first 30 minutes is 0.2 km per min.
How to get the average speed?Here we have the graph for the position of a bycicle rider on a 42-minute trip.
On the vertical axis we can see the position, and on the horizontal axis we can see the time.
Remember that:
speed = distance/time.
To find the average speed on the first 30 min, we need to take the quotient between the position after 30 minutes and 30 min.
At 30 min we can see that the position is at 6 km, then the speed will be:
S = 6km/30min = 0.2 km per min.
Learn more about speed at:
https://brainly.com/question/4931057
#SPJ1
The following sets of numbers are possible side lengths of a triangle. Which of the following sets forms a Pythagoreantriple?18, 24,4245, 28.5315, 30.4533,77.22
Answers
45, 28, 53
Explanations:The pythagorean triple is an equation of the form:
a² + b² = c²
Since the question states that the set of numbers are possible side lengths of a Pythagorean triple, the longest value in the set will be considered as the hypotenuse.
Considering the sets one after the other:
For the set (18, 24, 42)
18² + 24² ≠ 42²
For the set (45, 28, 53)
45² + 28² = 53²
Since this obeys a² + b² = c², the set (45, 28, 53) forms a Pythagorean triple.
All other sets do not obey the rule a² + b² = c², therefore, they do not form the Pythagorean triple.
two lines in the coordinate plane has opposites slopes, are parallel, and the sum of theie y-intercepts is 12. if one of the lines passes through (2,3) what are equarions of the lines?

Answers
y = 3
y = 9
Explanation:For two lines to be parallel, their slope must be equal.
Now, we are told the lines have opposite slopes. This means the slopes are 0.
This because the slopes need to be the same and be opposite to each other.
The only number with this characteristic is 0.
The opposites are 0 and -0. Both are equal to zero.
The equation of line with slope zero, will have a constant y coordinate.
This because: y = mx + c
when m = 0, we will be left with:
y = c = y-intercept
GIven poin: (2, 3) = (x, y)
In our question, the y coordinate from the point given is 3
The equation of one the line: y = 3
we are told the sum of the y intercept of both lines = 12
since the first y-intercept = 3
1st y-intercept + 2nd y- intercept = 12
The second y-intercept = 12 - 3 = 9
slope of the second one is also 0, y = c = y-intercept
The equations of the line:
y = 3
y = 9
we complete the sentence:
The equations of the lines are y = 3 and y = 9; parallel lines have same slopes;
So if slopes are opposites, the slopes must be zero. A line with the slope and passing through (2, 3) has an equation y = 3
Help with the following equation 8x²-6x-5=x
Answers
Answer:
\(8 {x}^{2} - 6x - 5 = x\)
\(8 {x}^{2} - 7x - 5 = 0\)
x = (7 + √((-7)^2 - 4(8)(-5)))/(2×8)
= (7 + √(49 + 160))/16
= (7 + √209)/16
= -.4661, 1.3411 (to 4 decimal places)
Mya is doing a 45-minute cardio workout. She has completed 4/5 of the workout. In how many minutes will her workout be done?
Answers
Answer:
9 minutes
Step-by-step explanation:
We can start by dividing 45 by 5, the denominator which is
9
then we can multiply that by the numerator 4, which is
36
finally, we subtract 36 from 45 which is
9