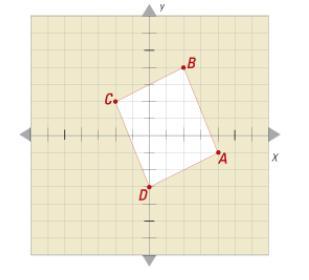
Is the following shape a square? how do you know?
A. No, the opposite sides are not parellel.
B. No, the sides are not congruent.
C. Yes, the adjacent sides are perpendicular, and all sides are the same length.
D. Yes, the opposite sides are parallel, and all sides are the same length.

Answer:

a. 4

b. -2

c. 0,5

Step-by-step explanation:

1. 4

2.2

3.0,5

IT IS SAYING TO WORK OUT WHAT THAT LINE REPRESENTS

If we are standing at a personal distance from someone, you are typically 18 inches to 4 feet apart. This range allows for comfortable interaction while still maintaining a sense of personal space.

To know more about distance visit:

https://brainly.com/question/31713805

#SPJ11

If you are standing a personal distance from someone, you are typically 18 inches to 4 feet apart. This range is commonly referred to as the "personal space" or "social distance" zone.

personal distance can vary depending on cultural norms and individual preferences. However, in general, this distance is considered a comfortable distance for conversation and interaction with friends, family, and acquaintances.

If you are standing closer than 18 inches, it is considered the "intimate distance" zone and typically reserved for romantic partners or close family members. If you are standing farther than 4 feet, it is considered the "public distance" zone and typically used for formal interactions or public speaking.

the distance between you and someone else when standing a personal distance away is typically between 18 inches to 4 feet. However, it is important to remember that personal distance can vary and be influenced by cultural norms and individual preferences. This long answer provides a comprehensive explanation of personal distance and its various zones.

To know more about  distance visit:

https://brainly.com/question/31713805

#SPJ11

The metric you provided describes a spatially flat and isotropic universe, where the line element incorporates the cosmic time, the scale factor for expansion, and the comoving radial and angular distances.

The metric you provided describes a spatially flat and isotropic universe, where the line element incorporates the cosmic time, the scale factor for expansion, and the comoving radial and angular distances.

The metric you mentioned is the line element of a spatially flat and isotropic universe, commonly known as the Friedmann-Robertson-Walker (FRW) metric. In this metric, the line element, ds², is given by:

ds² = -dt² + a(t)² [dr² + r²(dθ² + sin²θdϕ²)]

Here, t represents the cosmic time, a(t) is the scale factor representing the expansion of the universe, r is the comoving radial distance, θ is the co-latitude, and ϕ is the azimuthal angle.

Let's break down the components of the metric:

1. -dt²: This term represents the time interval squared, with a negative sign indicating a spacelike separation in the metric.

2. a(t)²: This term represents the scale factor squared, which describes the expansion of the universe. The scale factor determines the size of the universe at a given time, with a(t) = 1 representing the present size.

3. dr²: This term represents the comoving radial distance squared. It measures the physical distance from the observer (at a fixed point) to a point in space, accounting for the expansion of the universe.

4. r²(dθ² + sin²θdϕ²): This term represents the angular part of the metric. It involves two components: dθ² represents the infinitesimal change in the co-latitude θ, and sin²θdϕ² represents the infinitesimal change in the azimuthal angle ϕ, both squared and scaled by the comoving radial distance squared.

In summary, the metric you provided describes a spatially flat and isotropic universe, where the line element incorporates the cosmic time, the scale factor for expansion, and the comoving radial and angular distances.

To know more about scale factor click-
https://brainly.com/question/2826496
#SPJ11

Answer:In order for a set of numbers to represent the three sides of a triangle, they must satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides must be greater than the length of the third side. Let’s consider each set of numbers in turn to see if they meet this condition.The set {15,27,43} does not represent the sides of a triangle, as 15 + 27 < 43, which violates the triangle inequality theorem. In other words, the sum of the first two sides is not greater than the third side, so a triangle cannot be formed with these side lengths.The set {7,22,28} does represent the sides of a triangle. To see this, we can check that each pair of sides satisfies the triangle inequality theorem: 7 + 22 > 28, 7 + 28 > 22, and 22 + 28 > 7. Therefore, a triangle can be formed with these side lengths.The set {14,17,32} does not represent the sides of a triangle, as 14 + 17 < 32, violating the triangle inequality theorem. Therefore, a triangle cannot be formed with these side lengths.The set {8,19,27} does represent the sides of a triangle. We can check that each pair of sides satisfies the triangle inequality theorem: 8 + 19 > 27, 8 + 27 > 19, and 19 + 27 > 8. Therefore, a triangle can be formed with these side lengths.In general, when considering whether a given set of numbers represents the sides of a triangle, we must check that the sum of any two sides is greater than the length of the third side. This inequality is essential for ensuring that the three sides can form a closed shape. If this condition is not satisfied, the set of numbers cannot represent the sides of a triangle. Conversely, if the condition is satisfied, then a triangle can be formed with those side lengths.

Step-by-step explanation:

By using factoring by grouping or synthetic division, we find that \(x = -2\) is a real solution.

Checking for Rational Roots

Using the rational root theorem, the possible rational roots of the polynomial are given by the factors of the constant term (24) divided by the factors of the leading coefficient (-4).

The possible rational roots are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.

By substituting these values into \(f(x)\), we find that \(f(-2) = 0\). Hence, \(x + 2\) is a factor of \(f(x)\).

Dividing \(f(x)\) by \(x + 2\) using long division or synthetic division, we get:

Now, we have reduced the problem to factoring \(-4x³ + 18x² - 16x + 12\).

Attempt 2: Factoring by Grouping

Rearranging the terms, we have:

Factoring out common factors, we obtain:

Now, we have \(2x^2(-2x + 9) + 4(4x - 3)\). We can further factor this as:

Therefore, the fully factored form of \(f(x) = -4x⁴  + 26x³  - 50x² + 16x + 24\) is \(f(x) = (x + 2)(2x² + 4)(-2x + 9)\).

Solutions to the polynomial equations:

Using polynomial division or synthetic division, we can find the quadratic equation \((x + 2)(x² + 2x - 3)\). Factoring the quadratic equation, we get \(x² + 2x - 3 = (x +

Learn more about synthetic division

brainly.com/question/28824872

#SPJ11

Answer:

The length is 9 feet and the width is 4 feet.

Step-by-step explanation:

Let the dimensions be L (the length)  and L - 5 (the width).

From the given information the area is:

A = L(L - 5)

When L becomes L + 3 and width becomes (L - 5) -1  = L - 6 we have:

A = (L + 3)(L - 6) so

L(L - 5) = (L + 3)(L - 6)

L^2 - 5L = L^2 - 3L - 18

-2L  = -18

L = 9

so the width = 9 - 5 = 4.

Answer:

36

Step-by-step explanation:

I don’t know if this half the problem or something because you only need to know what a equals but...

1. Substitute x for 4 since x=4... so the equation would then be (4)^2+10(4)-20

2. You simplify so 4 squared is 16 because when you square something you times it by it self so 4^2 is simply 16 because 4*4=16 then 10*4 is 40 so then you get 16+40-20

3. So you can simplify that again to 56-20 and then to 36

Sorry I’m really bad at explaining but I hope this helps

Answer:

7. -3

8. 4.4

9. 11

On average, it would take approximately 3.33 tosses until Sophie catches a ball.

The scenario involves Sophie, a dog who loves playing catch but has a low probability of actually catching the ball, at 0.3.

also to know the number of tosses required until Sophie catches a ball, which can be denoted as x.

To determine the expected number of tosses required until Sophie catches a ball, we can use the concept of geometric distribution. In this case, the probability of success (Sophie catching the ball) is 0.3, and the number of tosses until the first success (Sophie catching the ball for the first time) is x.

The expected value of the geometric distribution is given by the formula E(x) = 1 / p, where p is the probability of success. Therefore, in this case, the expected number of tosses until Sophie catches a ball is:

E(x) = 1 / 0.3
E(x) ≈ 3.33

So, on average, it would take approximately 3.33 tosses until Sophie catches a ball.

To know more about probability visit:

https://brainly.com/question/31828911

#SPJ11

The simplification of four fourths over nine written as 4/4 ÷ 9 is given by 1/9

Fraction refers to a number which consists of a numerator and a denominator.

A numerator is the upper or top value of a fraction while a denominator is the lower or bottom value of a fraction.

Given: four fourths over nine

= 4/4 ÷ 9

= 1 ÷ 9

= 1/9

Or alternatively

4/4 ÷ 9

= 4/4 × 1/9

= (4 × 1) / (4 × 9)

= 4/36

= 1/9

In conclusion, the fraction four fourths over nine is simplified as 1/9

Read more on fraction simplification:

https://brainly.com/question/11562149

#SPJ1

This equation holds true, which confirms that AB is indeed the hypotenuse of the right triangle.

If the Pythagorean equation holds for all right triangles and ∠C is a right angle, then we can use the Pythagorean theorem to show that side AB is indeed the hypotenuse of the triangle.

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

So in this case, we have side AB as the hypotenuse, and sides AC and BC as the other two sides.

According to the Pythagorean theorem, we have:
AB^2 = AC^2 + BC^2

Since ∠C is a right angle, AC and BC are the legs of the triangle. By substituting these values into the equation, we get:
AB^2 = AC^2 + BC^2
AB^2 = AB^2

This equation holds true, which confirms that AB is indeed the hypotenuse of the right triangle.

Know more about hypotenuse here:

https://brainly.com/question/2217700

#SPJ11

Answer:

f(x) = |x| represents the modulus function or absolute value function. It gives us the distance between any point and the origin. Since distance can never be negative so we always consider its positive value only. You can simply multiply the given value with ‘-1’(if the given value is negative).

Step-by-step explanation:

Answer:

7.4%

Step-by-step explanation:

Given parameters:

Population of Latvia in 1989 = 2700000

Population of Latvia in 1994  = 2500000

Unknown:

Percentage decrease in population  = ?

Solution:

The change in population;

  Change in population = 2700000-2500000 = 200000

Percentage decrease  = \(\frac{Population change }{Population in 1989} x 100\)

Percentage decrease  = \(\frac{200000}{2700000}\) x 100 = 7.4% decrease

The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.

The slope of the tangent line to the graph of the function y = x^4 - 10x^2 + 9 at x = 1 can be found by taking the derivative of the function and evaluating it at x = 1. The equation of the tangent line can then be determined using the point-slope form.

Taking the derivative of the function y = x^4 - 10x^2 + 9 with respect to x, we get:

dy/dx = 4x^3 - 20x

To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative:

dy/dx (at x = 1) = 4(1)^3 - 20(1) = 4 - 20 = -16

Therefore, the slope of the tangent line is -16.

To find the equation of the tangent line, we use the point-slope form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.

Given that the point of tangency is (1, y(1)), we substitute x1 = 1 and y1 = y(1) into the equation:

y - y(1) = -16(x - 1)

Expanding the equation and simplifying, we have:

y - y(1) = -16x + 16

Rearranging the equation, we obtain the equation of the tangent line:

y = -16x + (y(1) + 16)

To find the slope of the tangent line, we first need to find the derivative of the given function. The derivative represents the rate of change of the function at any point on its graph. By evaluating the derivative at the specific value of x, we can determine the slope of the tangent line at that point.

In this case, the given function is y = x^4 - 10x^2 + 9. Taking its derivative with respect to x gives us dy/dx = 4x^3 - 20x. To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative equation, resulting in dy/dx = -16.

The slope of the tangent line is -16. This indicates that for every unit increase in x, the corresponding y-value decreases by 16 units.

To determine the equation of the tangent line, we use the point-slope form of a linear equation, which is y - y1 = m(x - x1). We know the point of tangency is (1, y(1)), where x1 = 1 and y(1) is the value of the function at x = 1.

Substituting these values into the point-slope form, we get y - y(1) = -16(x - 1). Expanding the equation and rearranging it yields the equation of the tangent line, y = -16x + (y(1) + 16).

The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.

To learn more about tangent click here:

brainly.com/question/10053881

#SPJ11

There were 25 jars of Brand X sold.

To find out how many jars of each brand were sold, we can set up a system of equations based on the given information.

Let's assume that x represents the number of jars of Brand X sold and y represents the number of jars of the No-Name brand sold.

From the given information, we know that Brand X sells for $4.06 per jar and the No-Name brand sells for $3.37 per jar. We also know that 37 jars were sold for a total of $141.94.

Based on this information, we can set up the following equations:

1) x + y = 37   (equation 1, representing the total number of jars sold)
2) 4.06x + 3.37y = 141.94   (equation 2, representing the total cost of the jars sold)

To solve this system of equations, we can use the method of substitution or elimination. Let's use the substitution method.

From equation 1, we can express x in terms of y: x = 37 - y

Substituting this expression for x in equation 2, we get:

4.06(37 - y) + 3.37y = 141.94

Expanding and simplifying, we have:

150.22 - 4.06y + 3.37y = 141.94

Combine like terms:

-0.69y = -8.28

Dividing both sides by -0.69, we find:

y = 12

Now, we can substitute the value of y back into equation 1 to find x:

x + 12 = 37

Subtracting 12 from both sides, we get:

x = 25

Therefore, there were 25 jars of Brand X sold.

In summary, 25 jars of Brand X were sold.

To learn more about brand, refer below:

https://brainly.com/question/31963271

#SPJ11

Answer: y=3 is a polynomial function? Yes. The equation y=3 represents the function that maps all x values to 3

Step-by-step explanation:

The equation y= 3 represents a horizontal line, which will have exactly one intersection point with any vertical line. So it passes the vertical line test for a function too.

graph{y=3+0.0000001x [-10, 10, -5, 5]}

Answer:

-300

Step-by-step explanation:

The width of the rectangular garden is 6 meters. Hence, the correct answer is w = 6. Option B is correct answer.

The  rectangular garden has a perimeter of 42 meters. The length is 3 meters longer than twice the width.

We need to write and solve an equation using inverse operations to determine the value of w.

The perimeter of a rectangle is given by:

P = 2(l + w)

Where P is the perimeter, l is the length, and w is the width of the rectangle

.As per the question, the length is 3 meters longer than twice the width, so the length can be expressed as:

l = 2w + 3

The perimeter is given to be 42 meters, so we can write:

42 = 2(l + w)

Substituting the value of l from the above expression,

we get:

42 = 2(2w + 3 + w)

Simplifying, we get:

42 = 2(3w + 3)21 = 3w + 3

Subtracting 3 from both sides,

we get:

18 = 3w

Dividing both sides by 3,

we get:

w = 6

Therefore, the width of the rectangular garden is 6 meters.

Option B is correct.

For more question rectangular

https://brainly.com/question/31149376

#SPJ8

Answer:

What are the sets/the answer choices?

Step-by-step explanation:

Answer:

B 12 boys and 16 girls

Step-by-step explanation:

Make the ratios into fraction form. Simplify all of the fractions. The fraction that equals the original ratio is the correct answer. Dived both 12 and 16 by 4 and you get 3 and 4.

Brainliest please

Answer:

B

Step-by-step explanation:

Because 3 times 4 is 12 and 4 times 4 is 16 so that shows that they are equivalent hope it helps have a nice day

The maximum area that the farmer can enclose for the rectangular garden is 488 sq ft and the dimensions of the rectangular garden are 24ft and 12 ft respectively.

It is given that a farmer decided to enclose a rectangular garden with one side using the barn of a tree and other 3 sides with 48 ft of fencing.

Let the length of the rectangle be y and the breadth of the rectangle be u.

So perimeter of the fencing needed = y + 2u (as one side is barn)

∴ y + 2u = 48

⇒ y = 48 - 2u (equation 1)

Area = yu (equation 2)

Putting the value of variable y from equation 1 in equation 2 we have,

Area = (48-2u)u

∴ Area = 48u - 2\(u^{2}\)

⇒ Area = -2\(u^{2}\) + 48u

⇒ Area = -2(\(u^{2}\) - 24u)

⇒ Area = -2(\(u^{2}\) - 24u + 144) + 288   (using completing the square method)

⇒ Area = -2\((u-12)^{2}\) + 288

So the maximum area is 288 sq units as for any value of u the area value will decrease as seen from the above equation.

So if Area = 288

Then yu = 288

⇒ u = 288/y equation 3

Putting this value in Perimeter equation 1 we have,

y = 48 - 2u

⇒ y = 48 - 2 x \(\frac{288}{y}\)

⇒ \(y^{2} = 48y - 576\)

⇒ \(y^{2} - 48y + 576 = 0\)

⇒ \((y-24)^{2}\) = 0

Solving we get y = 24 ft

Hence the value of u is calculated as follows:

⇒ u = 288 / y

⇒ u = 288/ 24 = 12 ft

The maximum area that the farmer can enclose is 488 sq ft and the dimensions of the rectangle are 24ft and 12 ft respectively.

To learn more about perimeter click here:

https://brainly.com/question/2142493

#SPJ4

Answer:

12.6

Step-by-step explanation:

According to Pythagoras theorem

c²=a²+b²

c=√a²+b²

√4²+12²

√16+144

√160

12.6

Answer:

The Great Western Trail = 4,455 miles

Step-by-step explanation:

The Iditarod Trail = 1,025 miles long

The Great Western Trail is 355 miles longer than 4 times the length of the Iditarod Trail.

The Great Western Trail = (4 × 1,025) miles + 355 miles

= 4,100 miles + 355 miles

= 4,455 miles

The Great Western Trail = 4,455 miles

The following statements are true:

81 is a perfect square.

729 is a perfect cube.

We have,

- 81 is a perfect square because it can be expressed as the square of a whole number.

In this case, 81 is equal to 9², where 9 is the square root of 81.

- 729 is a perfect cube because it can be expressed as the cube of a whole number.

In this case, 729 is equal to 9³, where 9 is the cube root of 729.

The statement "81 is both a perfect square and a perfect cube" is incorrect. While 81 is a perfect square, it is not a perfect cube because it cannot be expressed as the cube of a whole number.

Thus,

The following statements are true:

81 is a perfect square.

729 is a perfect cube.

Learn more about expressions here:

https://brainly.com/question/3118662

#SPJ6

The estimate of the mean length of the insects Ciara found is 17 millimeters (mm).

To calculate an estimate of the mean length of the insects Ciara found, we need to find the weighted average of the lengths using the given frequencies.

Let's denote the lower limits of the length intervals as L1 = 0, L2 = 10, and L3 = 20.

Similarly, denote the upper limits as U1 = 10, U2 = 20, and U3 = 30.

Next, we calculate the midpoints of each interval by taking the average of the lower and upper limits.

The midpoints are M1 = (L1 + U1) / 2 = 5, M2 = (L2 + U2) / 2 = 15, and M3 = (L3 + U3) / 2 = 25.

Now, we can calculate the sum of the products of the frequencies and the corresponding midpoints.

This gives us (5 \(\times\) 5) + (6 \(\times\) 15) + (9 \(\times\) 25) = 25 + 90 + 225 = 340.

Next, we calculate the sum of the frequencies, which is 5 + 6 + 9 = 20.

Finally, we divide the sum of the products by the sum of the frequencies to find the weighted average, which is 340 / 20 = 17.

Therefore, the estimate of the mean length of the insects Ciara found is 17 millimeters (mm).

Thus, the mean length of the insects Ciara found is approximately 17 millimeters (mm).

For similar question on mean length.

https://brainly.com/question/16971437  

#SPJ8

Answer: 2

Step-by-step explanation:

Thus, the explicit formula for the simple interest sequence A(n) = P + (n-1)(i.P) is: A(n) = P * (1 + i * (n-1)).

Simple interest is a method of calculating interest on a loan or investment where interest is charged only on the initial principal amount. In simple interest, the interest rate is applied to the original principal amount, and the interest earned remains the same throughout the entire term of the loan or investment.

by the question.

The formula for a simple interest sequence A(n) = P + (n-1) (i.P) represents the value of an investment that earns simple interest over n periods, where:

A(n) is the value of the investment after n periods.

P is the principal or initial investment

i is the interest rate per period as a decimal fraction (e.g. 0.05 for 5%)

n is the number of periods

To derive the explicit formula for A(n), we can use the formula for simple interest:

I = P * i * n

where I am the total interest earned over n periods. We can then express A(n) as:

A(n) = P + I

Substituting the expression for I, we get:

A(n) = P + P * i * (n-1)

Simplifying, we can factor out P to get:

A(n) = P * (1 + i * (n-1))

To learn more about amount:

https://brainly.com/question/13024617

#SPJ1

Answer your answer is correct it is 9

Step-by-step explanation:

Answer:your correct! btw heyy

Step-by-step explanation:

To order a calzone with 6 distinct topping from available list of 8 vegetarian toppings, number of choices of calzone available is 28.

Therefore, the answer is 28.

Total number of available toppings equals 8 and the number of toppings selecting is 6.

The number of ways calzone can be chosen with 6 distinct topping from 8 vegetarian toppings can be obtained by combination formula.

nCm = n!/ (m! × (n - m)!)

Therefore, the number of ways = nCm

= 8C6

= 8!/ (6! × (8 - 6)!)

= 8!/ (6! × 2!)

= (8 × 7)/ 2

= 28

To know more on combination

https://brainly.com/question/29764089

#SPJ4

Answer:

y=2x+10

Step-by-step explanation:

First, let's put the equation into slope-intercept form. We get y=2x-3/2.

Parallel lines have the same slope, so the slope of the line will be 2.

We then substitute the point into the equation to find the y-intercept.

We get y=2x+10

Hope this helps :-)