Answers
a. If s(t) is the displacement at time t, then the net displacement over the interval [0, 2] is
∆s = s(2) - s(0) = (2² - 3•2 + 2) - (0² - 3•0 + 2) = -2
The average velocity over this interval is
v [ave] = ∆s/∆t = -2/(2 - 0) = -1
b. Differentiate s with respect to t to get the velocity at time t :
v(t) = ds/dt = 2t - 3
At t = 0, the velocity is v(0) = 2•0 - 3 = -3, so the speed here is 3.
At t= 2, the velocity is v(2) = 2•2 - 3 = 1.
Differentiate again to get the acceleration:
a(t) = dv/dt = 2
so that a(0) = a(2) = 2.
c. The body changes direction when its velocity changes sign. In other words, its moves forward relative to its starting position if v(t) > 0, and backward if v(t) < 0.
The moment of changing direction happens when v(t) = 0. Solve for t :
2t - 3 = 0 ⇒ t = 3/2
Related Questions
The random variable X has a p.d.f P(X=x) foe x= 1,2 3 as shown below
E(x)=∑ XiPi
Find
i) E(x)
ii) E(3)
ii) E(x²)
iv) E(5x+3)

Answers
The random variable X has a pdf P(X=x) for x = 1,2,3 then,
1) E(x)= 2.2
2) E(3) = 0.9
3) E(x²) = 2.26
4) E(5x + 3)= 14.
Probability Density Function (pdf) is a statistical expression that defines a probability distribution for a discrete random variable as opposed to a continuouse random variable.
We have given that,
E(x) = ∑xipi
1) E(x) = ∑xipi
= x₁p₁ + x₂p₂ + x₃p₃
= 1(0.1) + 2(0.6) + 3(0.3)
= 0.1 + 1.2 + 0.9
E(x) = 2.2
2)E(3) = x₃p₃
= 3(0.3)
E(3) = 0.9
3) E(x²) = ∑xi²pi²
= x₁²p₁² + x₂²p₂² + x₃²p₃²
= 1(0.1)² + 4(0.6)² + 9(0.3)²
= 0.01 + 1.44 + 0.81
E(x²) = 2.26
4) E(5x + 3) = ∑5(xipi) + 3
= (5x₁p₁ + 5x₂p₂ + 5x₃p₃) + 3
= (5(0.1) + 10(0.6) + 15(0.3)) + 3
= 0.5 + 6 + 4.5 + 3
E(5x + 3) = 14
Therefore the random variable X has a pdf P(X=x) for x = 1,2,3 is
E(x) = ∑xipi then E(x) = 2.2, E(3) = 0.9, E(x²) = 2.26 and E(5x + 3) = 14.
To know more about variable here
https://brainly.com/question/29052310
#SPJ4
721.60 divided by 80
Answers
hope this helps !!
graph y-intercept 6 and slope-7
Answers
We will get y = -7x + 6 in graph y-intercept 6 and slope-7.
The equation of the line with a y-intercept of 6 and a slope of -7 can be written in slope-intercept form as:
y = mx + b
where m is the slope and b is the y-intercept.
Substituting the given values, we get:
y = -7x + 6
So the equation of the line is y = -7x + 6.
slope -7 and y - intercept 6.
Slope intercept form: y = mx + b, m=slope, b = y-intercept
y = -7x + 6
Just plug in a value for x and solve for y
x y=-7x+6
------------------
0 6
1 -1
If you plot these two points and draw a straight line through them,
that is the graph of the line.
for similar questions on graph
https://brainly.com/question/29538026
#SPJ11
Which two expressions are equivalent? B. A 4(2 + x) 4.2 +2.x 4 + 2 + x (4 + 2) + X D. C. 4. X + 2 4. (x + 2) 4 = (2-x) 4- 2 = X
Answers
What are the coordinates of point A?
A: (- 2, -6)
B: (- 6, -2)
C: (- 6, -3)
D: (- 3, -6)
Answer correctly for 50 points.
Answer falsely , then get ready for instant consequences.

Answers
The x value is first and the y value is second.point A is at (-3,-6)
4 Twice the sum of two numbers is 36. If one of the numbers is 10, Twenty years from now, I will be 4 times as old as my present age. What is my present age
Answers
Answer:
7
Step-by-step explanation:
The sum of the two number is 10 + x, which when doubled equals 36. Divide the 36/2, which gets to 18. Move the 10 to the other side which gets 18-10 to get 8. 20 years from now, so add 20. 20+8 is 28. 4 times my present age. So do the inverse and you will get 28/4 which equals 7. You're present age is 7.
Divide 0.4 / 41 Enter your answer as a decimal in the box.
Answers
Answer:
0.4 / 41=0.009760
It starts to repeat the same numbers
Step-by-step explanation:
At Ralphs 5 tomatoes cost $1.80.
At Vons 3 tomatoes cost $1.14.
Which is the better buy?
Answers
Answer:
I think 5 tomatoes cost $1.80
Answer:
Ralphs.
Step-by-step explanation:
Ralphs:
5 tomatoes = $1.80
1 tomato = $0.36
Vons:
3 tomatoes = $1.14
1 tomato = $0.38
Hence, Ralphs would be a better buy.
a group of friends every time they play a game of marbles, they lose 5 marbles as it’s a big playground and they can’t be bothered to look for marbles that roll away somewhere. every time a game of marbles ends (each game takes 10-15 minutes), they collect all their marbles in a big box, hide it behind a tree, and go for a quick run. every time these kids hide all their marbles in a box behind the tree, a very intelligent squirrel sneaks up to the box, and if there are more than 12 marbles in it, the squirrel steals 3 marbles and runs off. if this group of kids started with 120 marbles in total, how many games can they play in total before they have less than 10 marbles left (given that they lose some marbles each time they play, and a squirrel steals some marbles each time they go for a run).
Answers
Answer:
14 gamesStep-by-step explanation:
Initial number of marbles = 120Lost at every game = 5Stolen by a squirrel = 3Left = less than 10Let the number of games be x
then lost marbles = 5xstolen marbles = 3xInequality:
120 - 5x - 3x < 10120 - 8x < 10110 < 8xx > 110/8x > 13 rounded downSince there should be more than 0 left, another inequality for it:
120 - 8x > 0120 > 8x x < 15So 13 < x < 15, which leaves us with 14
Write this statement in your own words: ∃x ∈ ℕ, y ∈ ℤ|x² = y² Rewrite this using the appropriate mathematical notation: Even numbers are in the set of integers.
Answers
Answer:
See below.
Step-by-step explanation:
1)
So we have:
\(\exists x\in\mathbb{N},y\in\mathbb{Z}|x^2=y^2\)
This can be interpreted as:
"There exists a natural number x and an integer y such that x² is equal to y²."
2)
So we want even numbers are in the set of integers.
\(\{2n:n\in\mathbb{Z}\}\in\mathbb{Z}\)
This is interpreted as:
"The set of even numbers (2n such that n is an integer) is in the set of integers"
For two n by n square matricies A and B,
suppose rankA = rankB = n-1.
Can rank(AB) become less than n-1 ?
(e.g. rank (AB) = n-2)
If so, I humbly ask you for an example.
Thank you very much.
Answers
No, the rank of the product of two n by n square matrices A and B, denoted as AB, cannot be less than n-1 if both A and B have ranks of n-1.
According to the Rank-Nullity theorem, for any matrix M, the sum of its rank and nullity is equal to the number of columns in M. In this case, the number of columns in AB is n, so the sum of the rank and nullity of AB must be n.
If rank(A) = rank(B) = n-1, it means that both A and B have nullity 1. The nullity of a matrix is the dimension of its null space, which consists of all vectors that get mapped to the zero vector when multiplied by the matrix. Since both A and B have rank n-1, their null spaces consist only of the zero vector.
Now, considering AB, if the rank of AB were less than n-1, it would mean that the nullity of AB is greater than 1.
However, this would violate the Rank-Nullity theorem since the sum of the rank and nullity of AB must be n, which is the number of columns.
Therefore, if rank(A) = rank(B) = n-1, the rank of AB cannot be less than n-1.
For more such questions on rank
https://brainly.com/question/28839672
#SPJ8
84.4% of what number is 19.412?
Answers
Answer: 22.4402
Step-by-step explanation:
Answer:
84.4% of 23 is 19.412.
Step-by-step explanation:
Let the unknown number be x.
Now, 84.4% of x = 19.412.
∴ (84.4 ÷ 100) × x = 19.412.
By simplifying the equation,
x = (19.412 × 100) ÷ 84.4
x = 1941.2 ÷ 84.4
∴ x = 23
Thus, 84.4% of 23 is 19.412.
To learn more about Percentages,
refer to the following question!
https://brainly.com/question/3079428
triangle inequality proof
/a + b/ ≤ /a/ + /b/
Answers
Answer:
a^2+b^2+2|a||b|≥a2+b2+2ab(|a|+|b|)2≥|a+b|2(∵∀x∈R;x2=|x|2)∴|a|+|b|≥|a+b|\
Step-by-step explanation:
Hey I need help can u just salve the following questions because I don't get it.

Answers
Answer:
I dont know but I can direct.
Step-by-step explanation:
The median is a middle number in a sorted, ascending or descending, list of numbers.
The quartile measures the spread of values above and below the mean by dividing the distribution into four groups.
The interquartile range describes the middle 50% of values when ordered from lowest to highest.
Answer: median: 133.5
first quartile: 128
third quartille: 139
interquartille range: 11
Step-by-step explanation:
How many fifths in 3/4?
Answers
Answer:
19
Step-by-step explanation:
5. Zoe and Claire are sisters. They are giving clues about their heights. Write an equation and
solve to determine the height of both Zoe and Claire.
#1: Claire is twice as tall as Zoe.
#2: Together, Claire and Zoe are
108 inches tall
Answers
Using a system of equations, it is found that:
Zoe is 36 inches tall.Claire is 72 inches tall.------------------------
The heights are unknown, so we are going to call it x and y.x for Claire, y for Zoe.Claire is twice as tall as Zoe, thus \(x = 2y\)Together, they are 108 inches tall, thus:\(x + y = 108\)
Since \(x = 2y\)
\(2y + y = 108\)
\(3y = 108\)
\(y = \frac{108}{3}\)
\(y = 36\)
\(x = 2y = 2(36) = 72\)
Zoe is 36 inches tall.
Claire is 72 inches tall.
A similar problem is given at https://brainly.com/question/17096268
A straight line l1 with equation 5x - 7 = 0 cuts the x axis at point A. Straight line l2 is perpendicular to straight line l1 and passes through point A. What is the coordinates of point A and the equation of the straight line l2?
Answers
The coordinates of point A are (7/5, 0), and the perpendicular line that also passes through that point is:
y = 0.
How to get the perpendicular line?Here we want to get a line perpendicular to:
5x - 7 = 0
Solving this for x, we get:
5x = 7
x = 7/5.
This is a vertical line, so the perpendicular line will be a horizontal line, which is of the form:
y = a.
We know that the line:
x = 7/5.
Cuts the x-axis at point A.
Remember that the x-axis as coordinates (x, 0).
So the coordinates of point A are (7/5, 0).
Now, the perpendicular line:
y = a
Needs to pass through the point (7/5, 0), so the value of a must be zero, then the line is:
y = 0.
Learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
Which expression is equivalent to 3/2

Answers
Answer:
C
Step-by-step explanation:
For each measurement in the first column, write the equivalent number of inches in the second column. MeasurementMeasurement in Inches5 feet 2 inches627 feet 3 inches6 feet 4 inches4 feet 8 inches4 yards
Answers
You are required to provide the measurement in inches for each measurement given on the left column. The first one is solved thus;
\(\begin{gathered} 5ft,2in \\ \text{Where 1 foot=12 inches, then} \\ (5ft\times12)+2in=60in+2in \\ (5ft\times12)+2in=62in \end{gathered}\)Therefore we shall use the same conversion rate of 12 inches equals 1 foot to solve the others as follows;
\(\begin{gathered} (1) \\ (7ft\times12)+3in=84in+3in \\ (7ft\times12)+3in=87in \end{gathered}\)\(\begin{gathered} (2) \\ (6ft\times12)+^{}4in=72in+4in \\ (6ft\times12)+4in=76in \end{gathered}\)\(\begin{gathered} (3) \\ (4ft\times12)+8in=48in+8in \\ (4ft\times12)+8in=56in \end{gathered}\)\(\begin{gathered} (4) \\ \text{Note that 1 yard=3 feet, which means} \\ 4\text{yards}=(4yd\times3)ft \\ 4\text{yards}=12ft \\ \text{Therefore,} \\ 12ft\times12=144in \\ \text{hence,} \\ 4\text{yards}=144in \end{gathered}\)Help me out with this simple stuff please and thank you. Anyone. Show work.
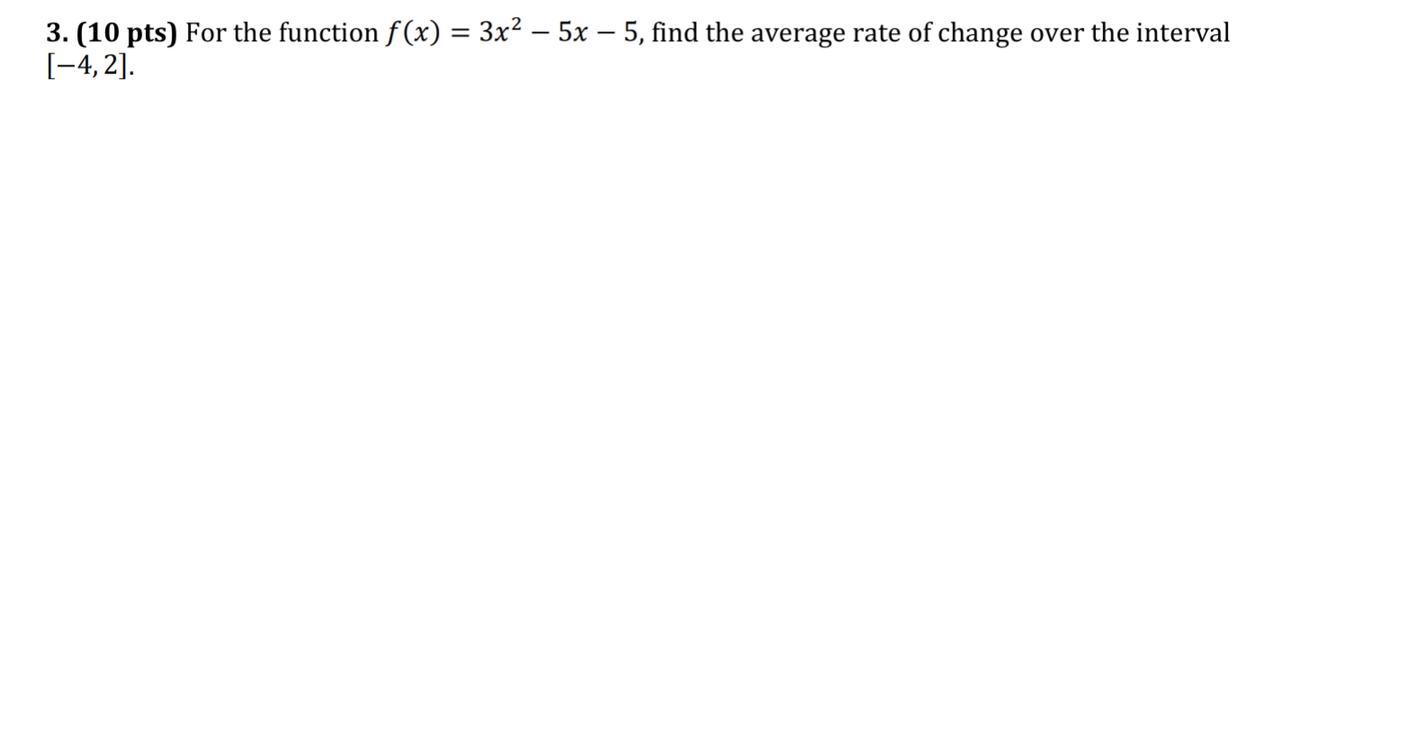
Answers
Answer:
The average rate of change of f on the interval [-4, -2] is -11.
Step-by-step explanation:
Recall that the average rate of change of a function over an interval is simply the slope of the line connecting the two endpoints.
Therefore, the average rate of change of f on the interval [-4, 2] equals:
\(\displaystyle f_\text{avg}(x) = \frac{f(2)-f(-4)}{2-(-4)}\)
Evaluate:
\(\displaystyle \begin{aligned} f_\text{avg}(x) & = \frac{f(2)-f(-4)}{2-(-4)} \\ \\ & = \frac{(-3)-(63)}{6} \\ \\ &= -11 \end{aligned}\)
In conclusion, the average rate of change of f on the interval [-4, -2] is -11.
what is between fractions 6/6 and 6/7
Answers
The fraction 13/7 lies between the fractions 6/6 and 6/7.
We have,
Between the fractions 6/6 and 6/7, there are infinitely many fractions.
To find a fraction that lies between these two fractions, we can take their average.
The fraction 6/6 simplifies to 1, and the fraction 6/7 cannot be simplified further.
To find the average, we add the two fractions and divide the sum by 2:
(6/6 + 6/7) / 2
To add the fractions, we need a common denominator, which is the least common multiple (LCM) of 6 and 7, which is 42.
Converting the fractions to have a common denominator:
(6/6) x (7/7) + (6/7) x (6/6) / 2
Simplifying the expression:
(42/42 + 36/42) / 2
Combining the numerators:
(78/42) / 2
Dividing:
78/42 = 13/7
Thus,
The fraction 13/7 lies between the fractions 6/6 and 6/7.
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ1
Solve 9x + 3y = 15 for y.
A. y=-3x + 15
B. y = 9x + 15
C. y = -9x + 5
D. y=-3x + 5
Answers
Answer: D) y = -3x + 5
Step-by-step explanation:
Move x.
3y = -9x + 15
Divide by 3.
y = -3x + 5
Hope it helps :) and let me know if you want me to elaborate.
Answer:
D. y = -3x + 5
Step-by-step explanation:
Subtract 9x from both sides
3y = 15 - 9x
y = 15/3 - 9x/3
y = 5 - 3x
y = -3x + 5
Crane Corporation is considering purchasing a new delivery truck. The new truck would cost $55,440. The new truck is expected to generate a cost savings of $7,700. At the end of 8 years, the company will sell the truck for an estimated $27,600.
Traditionally the company has used a rule of thumb that a proposal should not be accepted unless it has a payback period that is less than 50% of the asset's estimated useful life. Larry Newton, a new manager, has suggested that the company should not rely solely on the payback approach, but should also employ the net present value method when evaluating new projects. The company's cost of capital is 8%.
a) Compute the cash payback period and net present value of the proposed investment.
b) Does the project meet the company's cash payback criteria?
c) Does it meet the net present value criteria for acceptance?
Answers
A. The payback period is 7.2 years. The net present value of the proposed investment is 3720.55.
B. No, the project does not meet the company's cash payback criteria.
C. Yes, the project does meet the net present value criteria for acceptance.
How do we solve for the net present value of the proposed investment?A. The truck costs $55,440 and generates annual cost savings of $7,700. So the payback period is the cost of the truck divided the expected amount the truck will generate.
$55,440 / $7,700 = 7.2 years
To solve for the net present value, we say
Net Present Value = ∑ [(Cash inflow in period t) / (1 + \(r^{t}\)] - Initial Investment.
NPV = (($7,700 / (1 + 0.08)¹) = 7 129.63
+ ($7,700 / (1 + 0.08)²) = 6601.51
+ .($7,700 / (1 + 0.08)³ = 6112.51
+ ($7,700 / (1 + 0.08)⁴) = 5659.73
+ ($7,700 / (1 + 0.08)⁵) = 5240.49
+ ($7,700 / (1 + 0.08)⁶) = 4 852.31
+ ($7,700 / (1 + 0.08)⁷) = 4492.88
+($7,700 / (1 + 0.08)⁸) = 4160.07
+ ($27,600 / (1 + 0.08)⁸)) = 14911.42
- $55,440
We add all these values together and subtract by $55,440
7 129.63 + 6601.51 + 6112.51 + 5659.73 + 5240.49 +4 852.31 + 4492.88 + 4160.07 + 14911.42 - $55,440
59160.55 - 55,440
NPV = 3720.55
B. The cash payback period of the project is 7.2 years. The company's cash payback criteria state that a project should not be accepted unless it has a payback period that is less than 50% of the asset's estimated useful life, which would be 4 years which is 50% of 8 years. Since 7.2 years is greater than 4 years, the project does not meet the company's cash payback criteria.
C. The positive NPV of $3,720.55 shows that embarking on the prooject will be valuable to the company. This means the project meets the NPV criteria for acceptance.
Find more exercises on net present value;
https://brainly.com/question/27557482
#SPJ1
15 points
What is the slope of the line on the graph?
Enter your answer in the box.

Answers
The slope of the line on the graph is - 2
How to determine the slope?The given parameter is the line on the graph
From the above graph, we have the following points
(x₁, y₁) = (0, 0)
(x₂, y₂) = (3, -6)
The slope of a line can be calculated using the following slope formula
Slope = (y₂ - y₁)/(x₂ - x₁)
Where
(x₁, y₁) = (0, 0) and (x₂, y₂) = (3, -6)
Substitute the known values in the above equation
So, we have the following equation
Slope = (-6 - 0)/(3 -0)
Evaluate the quotient
Slope = -2
Hence, the slope is -2
Read more about slope at
https://brainly.com/question/3493733
#SPJ1
What is the segment units of RT

Answers
Answer:
RT = 81
Step-by-step explanation:
RT = RS+ST
13y – 23 = ( 6y+2) + (3y+7)
13y – 23 = 9y +9
13y – 9y = 9+23
4y = 32
y = 32/ 4
y=8
RT= 13y – 23 = 13 (8) – 23 = 104 – 23 = 81
___o___o___
If you want RS , ST
RS = 6y +2 = 6(8)+2 = 48 +2=50
ST = 3y +7 = 3(8) +7 = 24 + 7 =31
I hope I helped you^_^
Given that ABCDEF, solve for x.
A. 3
B. 2
OC. 6
D. 4

Answers
The value of side length x (DF) in the triangle is 4.
What is the value of x?The figures in the image is that of two similar triangle.
Triangle ABC is similar to triangle DEF.
From the diagram:
Leg 1 of the smaller triangle DE = 5
Leg 2 of the smaller triangle DF = x
Leg 1 of the larger triangle AB = 30
Leg 2 of the larger triangle AC = 24
To find the value of x, we take the ratio of the sides of the two triangle since they similar:
Hence:
Leg DE : Leg DF = Leg AB : Leg AC
Plug in the values:
5 : x = 30 : 24
5/x = 30/24
Cross multiplying, we get:
30x = 5 × 24
30x = 120
x = 120/30
x = 4
Therefore, the value of x is 4.
Learn more about ratios and proportions at :brainly.com/question/29774220
#SPJ1
help helllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllp

Answers
Answer:
159
Step-by-step explanation:
by expansion and simplifying:
100+64-5=159
Answer:
159
Step-by-step explanation:
You need to remember BIDMAS
B - brackets
I - indecieas 4 to the power of 5 for example
D - divide
M - multiply
A - add
S - subtract
Its the order in which you have to do everything.
So first do the brackets
3 + 5 = 8 and then do the indecies so 8 squared = 64
then do 10 cubed which is 100
for the moment we have 100 + 64 - 5
so the answer is 159
Hope this helps :D
At a cost of R55 per box how much would it cost to tile the training room
Answers
The total cost needed to tile the training room with an area of 100 m² is R110.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Let assume that the area of the trainig room is 100 m² and one box can complete 50 m², hence:
number of box needed = 100 m² / 50 m² = 2
Total cost = R55 per box * 2 box = R110
The total cost needed to tile the training room with an area of 100 m² is R110.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
HELP MEEEE PLS PLSSS PLSSSS HELP

Answers
Answer:
Step-by-step explanation:
-206
when you divide those two numbers you get a negative number and a decimal because you are dividing by a decimal with a negative sign.
Answer:
-21
...
I think, let me know if I'm wrong
Help me please will give brainlist

Answers
Answer: 691
Step-by-step explanation:
(17 + 6 + 9) × (19 + 16) - 19 × 7 - 6 × 4 - 16 × 17 = 691
