Jaxon goes to a store an buys an item that costs xx dollars. He has a coupon for 20% off, and then a 4% tax is added to the discounted price. Write an expression in terms of xx that represents the total amount that Jaxon paid at the register
Answers
An expression in terms of xx that represents the total amount that Jaxon paid at the register is 1.04 (xx - 0.20(xx)).
What is the total cost?The total cost is the amount calculated after any discount for an item and along with the tax incurred for an item to be purchased.
For the given situation,
Jaxon goes to a store and buys an item that costs xx dollars.
He has a discount coupon for 20%
Convert percentages to decimals = 0.20
The tax percentage is 4%
Convert percentages to decimals = 0.04
The discounted amount will get less than the cost price. So,
⇒ xx - 0.20(xx)
The tax amount for the item will get added to the final cost of the item. Thus the expression becomes,
⇒ 1.04 (xx - 0.20(xx))
Hence we can conclude that the expression for the total cost is 1.04 (xx - 0.20(xx))
For more questions on the total cost
https://brainly.com/question/22411938
#SPJ4
Related Questions
Inide a park of length 400m and breath 300m there i an area of walking track 4 m wide built all around. What i the area left for children for playing
Answers
The area left for children for playing 114464 sq. m
As per the given data inside a park:
The length of the park is 400 m
The breadth of the park is 300 m
The formula for the area of the park = Length × Breadth
= (400 × 300) sq. m
= 120000 sq. m
The width of the walking track inside the park is 4 m
The length of the park without the walking track
= 400 − (4 + 4) m
= 400 − 8 m
= 392 m
The breadth of the park without the walking track
= 300 − (4 + 2) m
= 300 − 8 m
=292 m
Area of the park without the walking track:
= 392 × 292
= 114464 sq. m
Therefore the area left for children for playing other than the walking track is 114464 sq. m.
For more questions on the area
https://brainly.com/question/17677554
#SPJ4
The selling price of a sweater is the cost plus the markup minus the discount. Write an expression to show the selling price s of a sweater. Use c for cost, m for markup, and d for discount.
Answers
Answer:
Step-by-step explanation:
Selling price = Cost price + Marked price - discount
s = c + m - d
Find the area of the surface obtained by rotating the circle
x2 + y2 = r 2
about the line
y = r.
Answers
The area of the surface obtained by rotating the circle \(x^2 + y^2 = r^2\) about the line y = r is π²r² square units.
To find the area of the surface obtained by rotating the circle
\(x^2 + y^2 = r^2\) about the line y = r, we can use the method of cylindrical shells.
The circle \(x^2 + y^2 = r^2\) is centered at the origin (0, 0) with a radius r. The line y = r is the line y-axis but shifted up by r units.
When we rotate the circle about the line y = r, it forms a 3D shape called a torus or a donut shape.
Consider a small strip on the circle at a distance y from the line y = r.
This small strip is at a distance r - y from the y-axis.
The length of this strip is the circumference of the circle at y, which is 2πy (since the circumference of a circle is 2π times its radius).
The width of this strip is the change in x, which we can denote as dx.
The area of this small strip is then given by the product of its length and width, which is 2πy dx.
Now, to find the total surface area, we integrate this area over the range of y values from -r to r (since the circle is symmetric about the y-axis):
Total Surface Area = ∫[from -r to r] 2πy dx
Now, we need to express y in terms of x using the equation of the circle \(x^2 + y^2 = r^2:\\y^2 = r^2 - x^2\)
y = ±√(r² - x²)
Since we are considering the upper half of the circle, we take the positive square root:
y = √(r² - x²)
Now, we can rewrite the integral with respect to x:
Total Surface Area = ∫[from -r to r] 2π√(r² - x²) dx
To solve this integral, we can make a trigonometric substitution:
Let x = r sin(θ), then dx = r cos(θ) dθ.
When x = -r, θ = -π/2, and when x = r, θ = π/2.
Now the integral becomes:
Total Surface Area = ∫[from -π/2 to π/2] 2π√(r² - (r sin(θ))²) (r cos(θ)) dθ
Total Surface Area = 2πr² ∫[from -π/2 to π/2] √(1 - sin²(θ)) cos(θ) dθ
Now, we can use the trigonometric identity:
sin²(θ) + cos²(θ) = 1
√(1 - sin²(θ)) = cos(θ)
Total Surface Area = 2πr² ∫[from -π/2 to π/2] cos²(θ) dθ
Now, use the trigonometric identity: cos²(θ) = (1 + cos(2θ))/2
Total Surface Area = 2πr² ∫[from -π/2 to π/2] (1 + cos(2θ))/2 dθ
Total Surface Area = 2πr² [θ/2 + (sin(2θ))/4] [from -π/2 to π/2]
Total Surface Area = 2πr² [(π/2 + sin(π) - (-π/2 + sin(-π)))/4]
Since sin(π) = 0 and sin(-π) = 0:
Total Surface Area = 2πr² [(π/2 - (-π/2))/4]
Total Surface Area = 2πr² (π/2)
Total Surface Area = π²r²
So, the area of the surface obtained by rotating the circle \(x^2 + y^2 = r^2\) about the line y = r is π²r² square units.
learn more on area of the surface click:
https://brainly.com/question/24126051
#SPJ4
The carousel at an amusement park has 20 horses spaced evenly around its circumference. The horses are numbered consecutively from 1 to 20. The carousel completes one rotation about its axis every 40 seconds.
a. What is the central angle, in degrees, formed by horse #1 and horse #8?
b. What is the speed of the carousel in rotations per minute?
c. What is the speed of the carousel in radians per minute?
d. A child rides the carousel for 6 minutes. Through how many radians will the child pass in the course of the carousel ride?

Answers
The child passes through 18π radians in the course of the carousel ride.
To determine the number of radians the child passes during the 6-minute ride on the carousel, we need to know the distance traveled in terms of radians.
Since there are 20 horses spaced evenly around the carousel, each horse is separated by an angle of 360/20 = 18 degrees or π/10 radians.
Therefore, during one rotation of the carousel, the child passes through 20π/10 = 2π radians. And since the carousel completes one rotation every 40 seconds, the angular velocity is 2π/40 = π/20 radians per second.
To find the total distance traveled in radians during a 6-minute ride, we need to multiply the angular velocity by the time elapsed.
6 minutes is equal to 360 seconds,
so the child passes through π/20 x 360 = 18π radians during the ride.
To learn more about : radians
https://brainly.com/question/29058626
#SPJ8
What is 3/5 −(−2 1/4)?
Write the answer as a mixed number in simplest terms.
Answers
Answer:
47/20 = 2 7/20 = 2.35
Step-by-step explanation:
3/5+2 1/4 = 3/5+9/4 = 3x4/20+9x5/20 = 12/20+45/20 = 47/20
2 7/20= 2.35
Answer:
-4 7/12 There hope the answer helps
Step-by-step explanation:
Find a when b = 6 and c =13/2
Formula: a(to the 2nd power)+ b(to the 2nd power) = c(to the 2nd power)
Answers
The value of variable a, when b = 6 and c =13/2 as given in the task content is; a = 2.5.
What is the value of a when b = 6 and c =13/2?It follows from the task content that the value of the variable, a in discuss be determined by means of the equation which relates all three variables;
a² + b² = c²
a² +6² = (13/2)²
a² = 42.25 - 36
a² = 6.25
a = 2.5
Ultimately, the value of variable a, when b = 6 and c =13/2 as given in the task content is; a = 2.5.
Read more on evaluating expressions;
https://brainly.com/question/3590570
#SPJ1
suppose two distinct integers are chosen from between $5$ and $17$, inclusive. what is the probability that their product is odd?
Answers
Since the two distinct integers are chosen from between 5 and 17, inclusive. The probability that their product is odd is 7/26.
Probability:
Probability means possibility. A branch of mathematics that deals with the occurrence of random events. Values are represented from 0 to 1. Probability was introduced into mathematics to predict the likelihood of an event occurring. Probability basically means how likely something is to happen. This is the basic theory of probability and is also used in probability distributions to learn the likely outcomes of random experiments. To determine the probability of a single event occurring, we first need to know the total number of possible outcomes.
According to the question:
In order for a product to be odd, both factors must be odd. That is because by definition a number with an even factor is even.
There are 13 numbers from 5 to 17 inclusive. 7 of them are odd. There is a 7/13 probability that the first number selected will be odd. Given that the first number selected is odd, there is a 6/12 = 1/2 probability that the next number will be odd given that the second number selected has to be different from the first.
= 7/13 × 1/2
= 7/26
Learn more about Probability:
https://brainly.com/question/30034780
#SPJ4
Given m || n, find the value of x and y

Answers
X = 21
Y = 30
X:
(3x - 15) + (6x + 6) = 180 -- combine like terms
9x - 9 = 180 -- add 9 to both sides
9x = 189
x = 21
Y:
Plug x into 3x-15
3(21) - 15 = y + 18
63 - 15 = y + 18
48 = y + 18 -- subtract 18 from both sides
y = 30
Can someone help me

Answers
The given table of the values of f(x) is used to complete the table for the function \(y = f \left( \frac{1}{5} \cdot x \right) \), to give;
The following values of x and y as follows;
x: -0.8, -0.2, 0, 0.6, 1.2
y: 7, -2, 3, -4, 5
Please also see the attached table
How can the function, f(x) be scaled to give the function, \(y = f \left( \frac{1}{5} \cdot x \right) \)?The question is with regards to scaling a graph horizontally.
Using the rule of scaling a graph, we have;
Given that a point on the graph of f(x) is (x, y), the corresponding point in the graph of f(C•x) is (C•x, y).
The given modification of the function is presented as follows;
\(y = f \left( \frac{1}{5} \cdot x \right) = f \left( 0.2 \cdot x \right)\)
The points on the graph that completes the table are therefore;
(0.2×(-4), 7) = (-0.8, 7)(0.2×(-1), -2) = (-0.2, -2)(0.2×0, 3) = (0, 3)(0.2×3, (-4)) = (0.6, -4)(0.2×6, 5) = (1.2, 5)The completed table is therefore;
x y
-0.8 7
-0.2. -2
0 3
0.6. -4
1.2. 5
Learn more about scaling of a function here:
https://brainly.com/question/3381225
#SPJ1

Solve ay+b = cx for y
Answers
Answer:
y=cx-b/a
Step-by-step explanation:
ay+b=cx
ay=cx-b
y=cx-b/a
Please help!
4. Evaluate | –2 | = ?
Answers
Answer:
that would equal 2 I hope this helps you
A triangle,ABC , has angle measures of 40, 40, 100 and and exactly two congruent (equal) sides. How would this triangle be classified?

Answers
Answer:
Step-by-step explanation:
Isosceles Obtuse.
It is obtuse because the largest angle is over 90.
It is Isosceles because the two base angles are equal.
If you get it wrong, it is because the question assumes that the two base angles are acute (which they are) but for this question I think you are referring to the lone angle at the top.
Find the value of B+4 when B=17
Answers
Answer:
Step-by-step explanation:
17 + 4 = 21
Answer:
B + 4 = 17+4
21 is the answer
Which one of the following modes of entry offers the highest level of control to the investing firms? a. Contractual Agreements b. Joint Venture c. Equity Participation d. FDI
Answers
DI is generally considered to provide the highest level of control to investing firms compared to other modes of entry.
The mode of entry that offers the highest level of control to the investing firms is d. FDI (Foreign Direct Investment).
Foreign Direct Investment refers to when a company establishes operations or invests in a foreign country with the intention of gaining control and ownership over the assets and operations of the foreign entity. With FDI, the investing firm has the highest level of control as they have direct ownership and decision-making authority over the foreign operations. They can control strategic decisions, management, and have the ability to transfer technology, resources, and knowledge to the foreign entity.
In contrast, the other modes of entry mentioned have varying levels of control:
a. Contractual Agreements: This involves entering into contractual agreements such as licensing, franchising, or distribution agreements. While some control can be exercised through these agreements, the level of control is typically lower compared to FDI.
b. Joint Venture: In a joint venture, two or more firms collaborate and share ownership, control, and risks in a new entity. The level of control depends on the terms of the joint venture agreement and the ownership structure. While some control is shared, it may not offer the same level of control as FDI.
c. Equity Participation: Equity participation refers to acquiring a minority or majority stake in a foreign company without gaining full control. The level of control depends on the percentage of equity acquired and the governance structure of the company. While equity participation provides some level of control, it may not offer the same degree of control as FDI.
to know more about participation visit:
brainly.com/question/30739789
#SPJ11
How do I write a phrase in words as an algebraic expression for 8/d?
Answers
Answer:
The quotient of 8 and d.
Step-by-step explanation:
I hope this helps you have a wonderful day! :D
This is URGENT! Please help me solve this question with full solutions

Answers
Answer:
B
Step-by-step explanation:
Given
\(\frac{1}{(t-2)^2}\) = 6 + \(\frac{1}{(t-2)}\) ( multiply through by (t - 2)²
1 = 6(t - 2)² + t - 2 ← distribute parenthesis and simplify
1 = 6(t² - 4t + 4) + t - 2
1 = 6t² - 24t + 24 + t - 2
1 = 6t² - 23t + 22 ( subtract 1 from both sides )
6t² - 23t + 21 = 0 ← in standard form
(2t - 3)(3t - 7) = 0 → in factored form
Equate each factor to zero and solve for t
2t - 3 = 0 ⇒ 2t = 3 ⇒ t = \(\frac{3}{2}\) ← p
3t - 7 = 0 ⇒ 3t = 7 ⇒ t = \(\frac{7}{3}\) ← q
Thus
p × q = \(\frac{3}{2}\) × \(\frac{7}{3}\) = \(\frac{21}{6}\) = \(\frac{7}{2}\) → B
Ms. Davis' is one less than 7 dozen. Ms. Davis is 7.2 more than 60% of her mother's age. Ms. Davis daughter is 3.5 more than 1/2 her mother's age. How old are ms. Davis, her mom, and her daughter?
Answers
Answer:
Ms. Davis=83 years
Her mom=126.33 years
Her daughter=66.67 years
Step-by-step explanation:
Let her mother's age=x
Ms. Davis= 7 dozens - 1
=(7*12)-1
=84-1
= 83 years
Ms. Davis= 7.2 + 60% of x
83=7.2 + .6x
83 - 7.2= .6x
75.8= .6x
Divide both sides by .6
75.8 / .6 = x
126.33 years
Ms. Davis daughter = 3.5 + 1/2 of x
=3.5 + 1/2(126.33)
=3.5 + 126.33 / 2
=3.5 + 63.165
=66.665
Approximately 66. 67 years
Suppose that $11,000 is invested in a savings account paying 5.3% interest per year. (a) Write the formula for the amount A in the account after t years if interest is compounded monthly. A(t)= (b) Find the amount in the account after 4 years if interest is compounded daily. (Round your answer to two decimal places.) (c) How long will it take for the amount in the account to grow to $20,000 if interest is compounded continuously? (Round your answer to two decimal places.)
Answers
The time taken for the amount in the account to grow to $20,000 if interest is compounded continuously is 10.37 years (rounded to two decimal places).
a) The formula for the amount A in the account after t years if interest is compounded monthly is:
\(A(t) = P ( 1 + r/n)^(nt)\)
Where,
P = $11,000
r = 0.053 / 12
= 0.0044166667 (monthly interest rate)
n = 12
t = number of years
So,
\(A(t) = 11,000 ( 1 + 0.0044166667)^(12t)\)
We simplify the equation as follows:
\(A(t) = 11,000 ( 1.0044166667)^(12t)\)
b) The amount in the account after 4 years if interest is compounded daily is $14,598.08 (rounded to two decimal places).
The formula for the amount A in the account after t years if interest is compounded daily is:
\(A(t) = P ( 1 + r/n)^(nt)\)
Where,
P = $11,000
r = 0.053 / 365
= 0.00014520548 (daily interest rate)
n = 365
t = 4 × 365
= 1460 (number of days)
So,
\(A(t) = 11,000 ( 1 + 0.00014520548)^(1460)\)
A(t) = 14,598.08
(rounded to two decimal places)
The amount in the account after 4 years if interest is compounded daily is $14,598.08.
c) The time taken for the amount in the account to grow to $20,000 if interest is compounded continuously is 10.37 years (rounded to two decimal places).
We use the formula:
\(A = Pe^(rt)\)
Where,
P = $11,000
r = 0.053
t = unknown
A = $20,000
We substitute the values and solve for t:
\(20,000 = 11,000e^(0.053t)\\t = ln(20,000/11,000) / 0.053\)
t = 10.37 years (rounded to two decimal places)
Know more about the compounded continuously
https://brainly.com/question/30460031
#SPJ11
Find a formula for the exponential function passing through thepoints (-1, 2/5 ) and (3,250)
Answers
The exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
what are functions?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output. Each function has a range, codomain, and domain. The usual way to refer to a function is as f(x), where x is the input. A function is typically represented as y = f. (x).
In mathematics, a function is a unique arrangement of the inputs (also referred to as the domain) and their outputs (sometimes referred to as the codomain), where each input has exactly one output and the output can be linked to its input.
from the question:
This is the shape of the exponential function:
f(x) = a *\(b^x\)
where a represents the starting point and b represents the exponential function's base.
We must solve the system of equations to determine the values of a and b that meet the requirements:
a * \(b^(-1)\) = 2/5 (equation 1)
a *\(b^3\)= 250 (equation 2)
We can solve for an in equation 1 by multiplying both sides by b:
a = (2/5) * b
Substituting this expression into equation 2, we get:
(2/5) * b *\(b^3\) = 250
Simplifying, we get:
\(b^4 = 3125\)
By combining the fourth roots from both sides, we arrive at:
b = 5
When we use the expression we discovered for a and this value of b, we get:
a = (2/5) * 5 = 2
As a result, the exponential function between (-1, 2/5) and (3, 250) is as follows:
\(f(x) = 2 * 5^x\)
to know more about functions visit:
https://brainly.com/question/12431044
#SPJ1
solve the equation -6=2(w+5)
Answers
-6=(2xw) +(5x2)
-6=2w+10
-16=2w
-8=w
Martha was recarpeting her bedroom, which was 15 feet long and 10 feet wide. How many square feet (the area) will she need to purchase?
Answers
Answer:
150 Square feet
Step-by-step explanation:
15 feet long
10 feet wide
Area = length x width
15 x 10 = 150
150 Square feet
Hope this helped!
For box plot data where Q1 = 200, Q2 = 250, and Q3 = 290, the
IQR
Answers
The value of IQR is 90 when box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290.
Given that,
For box plot data where Q₁ = 200, Q₂ = 250, and Q₃ = 290
We have to find the data of IQR.
We know that,
IQR is define as the variation in the distribution of your data's middle quartile is measured by the interquartile range (IQR). It is the range that corresponds to your sample's middle 50%. Measure the variability where the majority of your numbers are by using the IQR.
IQR Formula is Q₃ - Q₁
So,
Q₃ = 290
Q₁ = 200
Then ,
IQR = Q₃ - Q₁
IQR = 290 - 200
IQR = 90
Therefore, The value of IQR is 90.
To know more about IQR visit:
https://brainly.com/question/31207390
#SPJ4
Answer this ASAP will give the brainliest answer
Given that y = 8 cm and θ = 25°, work out x rounded to 1 DP.
The diagram is not drawn accurately.
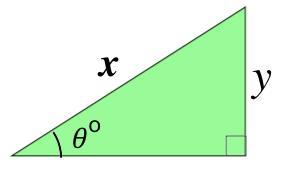
Answers
Answer: x = 18.9 to 1dp
Step-by-step explanation: Using SOH CAH TOA,
Sin 25 = 8/x
Making x subject of the formula:
x = 8/Sin 25
x = 18.92961267
x = 18.9 to 1dp
What is the value of KL

Answers
Answer:
40.5
Step-by-step explanation:
Since the centroid (the point of concurrency of the sides of a triangle) divides the 3 medians into the ratios from the point to the centroid to the centroid to the side into the ratio of 2:1. To find PK divide 27 by 2
27/2=13.5
Then add 27 and 13.5 to get KL
27+13.5=40.5
Find the value of x in the figure.

Answers
Answer:
x=28
Step-by-step explanation:
\(\huge\bold{To\:find:}\)
✎ The value of \(x\).
\(\large\mathfrak{{\pmb{\underline{\orange{Solution}}{\orange{:}}}}}\)
\(\sf\purple{The\:value\:of\:x\:is\:28°. }\)
\(\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\orange{:}}}}}\)
Since it is right-angle,
\(Sum \: of \: angles \: = 90° \\ ⇢ (2x + 1) + 33 ° = 90° \\ ⇢2x + 34° = 90° \\ ⇢2x = 90° - 34° \\⇢ 2x = 56° \\⇢ x = \frac{56° }{2} \\ ⇢x = 28° \)
\(\sf\blue{Therefore,\:the\:value\:of\:x\:is\:28°.}\)
\(\huge\bold{To\:verify :}\)
\((2x + 1) + 33° = 90° \\ ➡ \: 2 \times 28° + 1 + 33° = 90° \\ ➡ \: 56° + 34° = 90° \\ ➡ \: 90° = 90° \\ ➡ \: L.H.S.=R. H. S\)
Hence verified.
\(\circ \: \: { \underline{ \boxed{ \sf{ \color{green}{Happy\:learning.}}}}}∘\)

andrew wants the average of his five tests in science to be a 93. what score must he earn on the fifth test if his first four test grades are 87, 89, 97, and 95?
Answers
Andrew needs to score 99 on his fifth science test in order to have an average of 93 across all five tests.
To find out what score Andrew needs to earn on his fifth science test, we can use the concept of averages. The average of a set of numbers is calculated by adding up all the numbers and then dividing the sum by the total number of values.
Andrew has already taken four science tests, and their scores are given as 87, 89, 97, and 95. To calculate the average, we add up these four scores: 87 + 89 + 97 + 95 = 368.
Now, we need to consider the fifth test score that Andrew needs to achieve. Let's call it x. To have an average of 93 across all five tests, we need to divide the sum of all the scores (including the fifth test score) by 5 (the total number of tests): (368 + x) / 5 = 93.
We can solve this equation for x by isolating it on one side. Multiplying both sides by 5 gives us 368 + x = 465. By subtracting 368 from both sides, we find x = 465 - 368 = 97.
Therefore, Andrew needs to score 97 on his fifth science test to have an average of 93 across all five tests.
Learn more about average here:
https://brainly.com/question/24057012
#SPJ11
A vendor has 18 balloons for sale: 9 are yellow, 3 are red, and 6 are green. a balloon is selected at random and sold. if the balloon sold is yellow, what is the probability that the next balloon selected at random is also yellow? fraction 9 over 18 fraction 8 over 18 fraction 9 over 17 fraction 8 over 17.
Answers
When a vendor sell a yellow balloon randomly from 18 balloons for sale out of which 9 are yellow, 3 are red, and 6 are green, the probability that the next balloon selected at random is also yellow is 8/ 17.
Therefore the answer is 8 over 17.
There are total of 18 balloons for sale and out of that 9 are yellow.
After selling a yellow balloon, the total number of balloon remaining is
18 - 1 = 17
And the number of yellow balloon remaining is
9 - 1 = 8
So now the probability of selecting a yellow balloon randomly is given by dividing the number of yellow balloons remaining by the total number of balloon remaining, that is
Probability = 8/ 17
To know more on probability
https://brainly.com/question/14997732
#SPJ4
The diameter of a circle is 20 in. Find its area in terms of pi
Answers
Answer:
Is that your answer ☺️☺️☺️

The area of the circle formula is useful for measuring the space occupied by a circular field or a plot. A circle is a closed plane geometric shape. The area of the circle with diameter 20 in is 100 π inches².
What is area of a circle?The area of the circle is defined as the region occupied by the circle in a two dimensional plane. The diameter of the circle is the line which divides the circle into two equal parts and radius is half of the diameter.
The unit of area of a circle is m², cm², etc. The equation used to calculate the area of the circle is:
Area of a circle = π × r²
Here radius = 10 inches
Then the area of circle is given as:
Area = π × 10 × 10 = 100 π inches²
To know more about area of a circle, visit;
https://brainly.com/question/266951
#SPJ2
What is the equation of the line that passes through the points (1, -3) and (3, 5)? Write the equation in standard form AND using function notation.
Answers
Answer:
y= 4x-7
Step-by-step explanation:
I could be wrong this is what I got so I apologize if this is incorrect
Please help me with this math problem

Answers
Answer:
18vw²y^9 + 24v^6w^5
= 6vw²( 3y^9 + 4v^5w³)
Hope this helps.
Answer:
6vw^2(3y^9 + 4v^5w^3)
Step-by-step explanation:
If you were to multiply the equation 6vw^2(3y^9 + 4v^5w^3) then the result would be
18vw^2y^9 + 24v^6w^5
Hope this helps!