Jocelyn compiled data on the number of hours students work per week the summer after the senior year. The minimum number of hours in the distribution was 23. The range was 17. What is the maximum number of hours in the distribution.
Answers
Related Questions
The average price of a movie ticket in the United States from 1980 to 2000 can be modeled by the expression 2.75 + 0.10x, where x is the number of years since 1980.Which parts of the expression correspond to the cost of movie tickets in 1980 and the increase in price per year? Choose the correct value for each part below. Part A: The cost of movie tickets in 1980 is represented by
Answers
Answer:
\(2.75,\ 0.1x\)
\(2.75\)
Step-by-step explanation:
In the expression \(2.75+0.1x\) the number \(2.75\) represents the cost of a movie ticket in 1980 and \(x\) represents the years after 1980. So increase per year is represented by \(0.1x\).
If the cost of the ticket in 1982 is needed that means 2 years have passed after 1980, \(x\) will be \(2\).
In 1980, zero years have passed so, \(x=0\)
Therefore the cost of movie tickets is represented by \(2.75+0.1\times 0=2.75\)
Noah is studying a type of sea sponge that grows at a constant rate. They measured the age and height of 333 pieces of the sponge. Here's what they found:

Answers
Answer:
a = h/2 would be the answer.
Step;-
Find slope:-
m = rise/run = (16-8)/(8-4) = 8/4 = 2
Now,
y = mx + b
or, 8 = 2(4) + b
so, b = 0
So,
y = mx + b
or, h = 2a + 0
so, h = 2a
hence,a = h/2.
The sea sponges's height grows 2cm every 1 year, so you can write an equation to find the height at any age \(a = \frac{h}{2}\)
which number comes next in this series 5, 7, 11, 19, 35
Answers
Answer: 67
Step-by-step explanation:
We see a pattern where we multiply the number we added by previously by two.
For example, from 5 to 7, it is 2.
From 7 to 11, we add by 4.
From 11 to 19, we add by 8.
From 19 to 35, we add by 16.
This means the next number would be 32, adding 35 by 32 gives us 67,
what is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2? a. 1/6 b. 1/36 O c. 6 d. 36 e.60
Answers
The correct answer is option b. 1/36 is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2.
In unbiased point estimation, the expected value of the sample variance S2 is a crucial idea. When a sample is drawn from a population repeatedly, an average value of S2 is what is anticipated.
The population variance divided by the sample size represents the expected value of S2. It is, in other words, the population variance divided by n-1, where n is the sample size.
As a result, the expected value of the sample variance S2 for a sample size of 6 is equal to 1/36.
As a result, when a sample is drawn from a population repeatedly, the average value of S2 will be equal to 1/36 of the variance in the population.
Complete Question:
What is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2?
a. 1/6
b. 1/36
c. 6
d. 36
e.60
To learn more about unbiased visit:
https://brainly.com/question/22777338
#SPJ4
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. 9. y= x
,y=0,x=4
Answers
The volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells is 486π cubic units.
To find the volume generated by rotating the region bounded by the curve y = x about the y-axis using the method of cylindrical shells, we can follow these steps:
First, let's sketch the region bounded by the curve y = x. This is a straight line passing through the origin with a slope of 1. It forms a right triangle in the first quadrant, with the x-axis and y-axis as its legs.
Next, we need to determine the limits of integration. Since we are rotating about the y-axis, the integration limits will correspond to the y-values of the region. In this case, the region is bounded by y = 0 (the x-axis) and y = x.
The height of each cylindrical shell will be the difference between the upper and lower curves. Therefore, the height of each shell is given by h = x.
The radius of each cylindrical shell is the distance from the y-axis to the x-value on the curve. Since we are rotating about the y-axis, the radius is given by r = y.
The differential volume element of each cylindrical shell is given by dV = 2πrh dy, where r is the radius and h is the height.
Now we can express the volume of the solid of revolution as the integral of the differential volume element over the range of y-values:
V = ∫[a, b] 2πrh dy
Here, [a, b] represents the range of y-values that define the region. In this case, a = 0 and b = 9 (as y = x, so the curve intersects y-axis at y = 9).
Substituting t
he values of r and h into the integral, we have:
V = ∫[0, 9] 2πy(y) dy
Simplifying, we get:
V = 2π ∫[0, 9] y^2 dy
Evaluating the integral, we have:
V = 2π [y^3/3] from 0 to 9
V = 2π [(9^3/3) - (0^3/3)]
V = 2π [(729/3) - 0]
V = 2π (243)
V = 486π
to learn more about integration.
https://brainly.com/question/31744185
#SPJ11
-3x^2-3x+6 find the discriminant. Show your work
Answers
Answer:
81
Step-by-step explanation:
discriminant is b² - 4ac where a is coefficient in front of x², b is coefficient in front of x and c is constant term.
a = -3, b = -3, c = 6
b² - 4ac
= (-3)² - 4(-3)(6)
= +9 - 4(-18)
= 9 + 4X18
= 9 + 72
= 81
f(x)=x^2+x and g(x)=1/x+1 find the rules for (f o g)(x) and (g o f)(x) and give the domain of each composite function

Answers
The composite functions of (f o g)(x), (g o f)(x) and their domains in the function f( x ) = x² + x and g( x ) = 1/(x+1) are (x+2) / (x+1)², Domain: {x|x ≠ -1 } and 1/(x² + x + 1 ), Domain: {x|x ∈ R } respectively.
What are the composite result function and domain of (f o g)(x) and (g o f)(x) in the given function?A function is simply a relationship that maps one input to one output.
Given the data in the question;
f( x ) = x² + xg( x ) = 1/(x+1)(f o g)(x) = ?(g o f)(x) = ?First, set up the composite result function (f o g)(x).
(f o g)(x) = f( g(x) )
f( x ) = x² + x
f( g(x) ) = f( 1/(x+1) ) = ( 1/(x+1) )² + 1/(x+1)
Apply product rule to simply
f( g(x) ) = 1² /(x+1)² + 1/(x+1)
f( g(x) ) = (1 + x + 1 )/ (x+1)²
f( g(x) ) = (x+2) / (x+1)²
Next, find the domain by equating the denominator to 0 and solve for x.
x + 1 = 0
x = -1
Domain: {x|x ≠ -1 }
For (g o f)(x), set up the composite result function (g o f)(x).
(g o f)(x) = g( f(x) )
g( x ) = 1/(x+1)
g( f(x) ) = g( x² + x ) = 1/( (x² + x) + 1 )
g( f(x) ) = 1/( (x² + x) + 1 )
g( f(x) ) = 1/(x² + x + 1 )
Next, find the domain by equating the denominator to 0 and solve for x.
x² + x + 1 = 0
x = ( -1±√(1² - 4 ×(1×1) ) / (2 × 1 )
x = (-1±i√3)/2
x = (-1+i√3)/2, (-1-i√3)/2
Hence,
Domain is set of all real numbers.
Domain: {x|x ∈ R }
Therefore the composite functions and their domain are (x+2) / (x+1)², Domain: {x|x ≠ -1 } and 1/(x² + x + 1 ), Domain: {x|x ∈ R }.
Learn more about functions here: brainly.com/question/2541698
#SPJ1
2x + 3y =-15
what is the equation in slope- intercept form?
Answers
Answer:
Y = -2/3x - 5
Step-by-step explanation:
Hope this helps. Pls give brainliest.
Answer asap please in circle k with the measure of arc jl = 82 degrees find m angle jkl .
Answers
The without knowing the radius or diameter of circle K, we cannot determine the measure of angle JKL.
What is the probability of rolling a sum of 7 with two fair six-sided dice?To find the measure of angle JKL in circle K, we need to use the relationship between the measure of an arc and the measure of its corresponding central angle.
In a circle, the measure of an arc is proportional to the measure of its corresponding central angle.
The ratio between the measure of an arc and the measure of its corresponding central angle is equal to the ratio between the circumference of the circle and the total degrees in a circle, which is 360 degrees.
Let's denote the measure of angle JKL as x. Since the measure of arc JL is given as 82 degrees, we can set up the following proportion:
x degrees / 82 degrees = 360 degrees / total circumference
To solve for x, we need to determine the total circumference of circle K. If the radius or diameter of the circle is given, we can calculate the circumference using the formula C = 2πr or C = πd, respectively.
Without additional information about circle K, it is not possible to calculate the total circumference or determine the measure of angle JKL accurately.
To find the measure of angle JKL in circle K, we need to use the relationship between the measure of an arc and the measure of its corresponding central angle.
In a circle, the measure of an arc is proportional to the measure of its corresponding central angle.
The ratio between the measure of an arc and the measure of its corresponding central angle is equal to the ratio between the circumference of the circle and the total degrees in a circle, which is 360 degrees.
Let's denote the measure of angle JKL as x. Since the measure of arc JL is given as 82 degrees, we can set up the following proportion:
x degrees / 82 degrees = 360 degrees / total circumference
To solve for x, we need to determine the total circumference of circle K. If the radius or diameter of the circle is given, we can calculate the circumference using the formula C = 2πr or C = πd, respectively.
Without additional information about circle K, it is not possible to calculate the total circumference or determine the measure of angle JKL accurately.
Learn more about diameter
brainly.com/question/31445584
#SPJ11
Apply distributive property:
-6(2x+5)=
Answers
Answer:
-12x-30
Step-by-step explanation:
First you Distribute -6 times 2x= -12x
Then you multiply -6 times 5=-30
So it is -12x-30
Answer:
-12x-30
Step-by-step explanation:
-6*2x+(-6*5)=-12x-30
The mass of a pencil is 5.44 g. the mass of a crayon is 2.145 g. how much greater is the mass of the pencil than the mass of the crayon? enter your answer in the box.
Answers
Answer:7.585 g
Step-by-step explanation: i took the test trust me
Comparing the values by subtraction, the mass of the pencil is greater than the mass of the crayon by 3.295 g.
Using subtraction, two values can be compared by getting how much one exceeds the other.
If the mass of a pencil is 5.44 g and the mass of a crayon is 2.145 g, subtract the mass of the crayon from the mass of the pencil to know how much greater is the mass of the pencil compared to the mass of the crayon.
5.44 g - 2.145 g = 3.295 g
Hence, the mass of the pencil is greater than the mass of the crayon by 3.295 g.
Learn more about comparing values by subtraction here: brainly.com/question/66864
#SPJ4
Pls answer Subtract (17+4.5m+8k)-(7.5m-9+4k)

Answers
1/3 as a percent
0.43 as a percent
2/17 as a percent
1.25 as a percent
All rounded to the nearest whole
Answers
B.) .43 = 43%
C.) 2/17 = 12%
D.) 1.25 = 125%
A rectangular prism has a base that measures 5 centimeters by 3 centimeters and a height of 2 centimeters. Cameron fills the prism with
1
2
centimeter cubes. How many cubes will be on the bottom la
yer?
A.
120 cubes
b.
30 cubes
c.
60 cubes
d.15 cubes
Answers
Answer:
D. 15
Step-by-step explanation:
Assuming it's 1^2 cm cubes, or 1 square centimeter cubes, the answer is D. The base is 5 x 3 = 15 cm^2.
We can ignore the height, since we're only looking at the bottom layer.
Examine the following figures to find out the pattern. 5 figures. A figure with 3 sides, figure with 4 sides, figure with 5 sides, figure with 6 sides, figure with 7 sides. How many sides would the 10th figure in this sequence have? a. 10 sides b. 12 sides c. 13 sides d. 14 sides
HELP PLEASE AND QUICK
Answers
Answer:
B. 12 sides
Step-by-step explanation:
Correct on edge
Which theorem has two sides and a non-included angle?
Answers
Angle-Angle-Side (AAS) Theorem has two sides and a non-included angle.
What is Angle-Angle-Side (AAS) Theorem?The triangles are congruent if two angles and a non-included side in one triangle are congruent with two angles and the corresponding non-included side in another triangle, according to the Angle-Angle-Side (AAS) Congruence Theorem.The side-angle-side (SAS) theorem is the first such theorem. The triangles are congruent if two sides and the included angle of one triangle are equivalent to two sides and the included angle of another triangle.When two angles and an unincluded side of one triangle are equal to two angles and the corresponding unincluded side of the other triangle, two triangles are said to be congruent (AAS=AAS).To learn more about Angle-Angle-Side (AAS) Theorem refer to:
https://brainly.com/question/3168048
#SPJ4
I need the answer ASAP!!
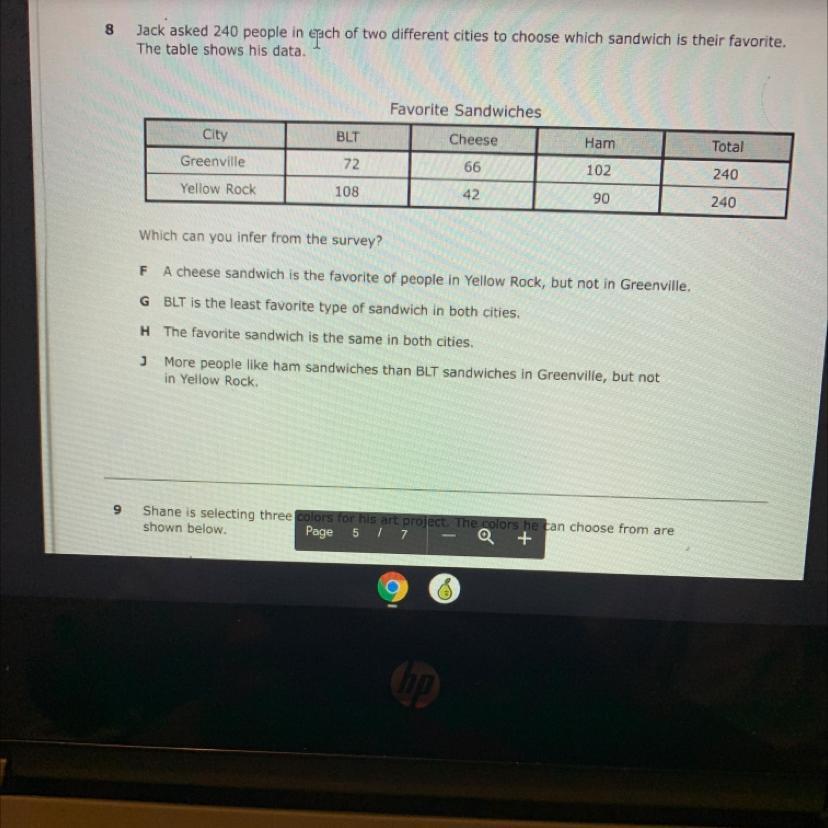
Answers
Answer:
I'm pretty sure the answer is J
Solving the Quadratic equations by completing the square: 2x^2-7x+2=0
Answers
Step-by-step explanation:
Check the above photos...



.1 The series Σ n=1 [infinity] 1/ √n (√n +1) (a) converges by the integral test (b) diverges by the ratio test (c) converges by the ratio test (d) diverges by the integral test (e) diverges by the nth term test of divergence.
Answers
The series Σ n=1 [infinity] 1/ √n (√n +1) is diverges by the ratio test, the correct answer is (b)
To determine whether the series Σ n=1 [infinity] 1/√(n(√n + 1)) converges or diverges, we can use the integral test.
The integral test states that if f(x) is a positive, continuous, and decreasing function on the interval [1, ∞) and if the series Σ n=1 [infinity] f(n) converges, then the integral ∫ 1 to ∞ f(x) dx also converges, and vice versa.
Let's evaluate the integral ∫ 1 to ∞ 1/√(x(√x + 1)) dx:
∫ 1 to ∞ 1/√(x(√x + 1)) dx = ∫ 1 to ∞ 1/(√x^3 + √x^2) dx
By simplifying the denominator, we get:
∫ 1 to ∞ 1/(x^(3/2) + x) dx
Now, let's evaluate this integral:
∫ 1 to ∞ 1/(x^(3/2) + x) dx = ∫ 1 to ∞ 1/x(x^(1/2) + 1) dx
To evaluate the integral, we can perform a u-substitution, where u = x^(1/2) + 1:
Taking the derivative of both sides, we get du = (1/2)x^(-1/2) dx
Rearranging, we have dx = 2u du
Substituting the values into the integral, we get:
∫ 1 to ∞ 1/(x^(3/2) + x) dx = ∫ 1 to ∞ 1/(u^2 - 1) * 2u du
Simplifying, we have:
∫ 1 to ∞ 1/(u - 1)(u + 1) du
Now, we can perform partial fraction decomposition:
1/(u - 1)(u + 1) = A/(u - 1) + B/(u + 1)
Multiplying through by (u - 1)(u + 1), we get:
1 = A(u + 1) + B(u - 1)
Expanding, we have:
1 = (A + B)u + (A - B)
By comparing coefficients, we find A - B = 0 and A + B = 1, which gives A = 1/2 and B = 1/2.
Now, we can rewrite the integral as:
∫ 1 to ∞ (1/2)/(u - 1) + (1/2)/(u + 1) du
Taking the integral, we get:
(1/2)ln|u - 1| + (1/2)ln|u + 1| + C
Substituting back u = x^(1/2) + 1, we have:
(1/2)ln|x^(1/2) + 1 - 1| + (1/2)ln|x^(1/2) + 1 + 1| + C
Simplifying, we get:
(1/2)ln|x^(1/2)| + (1/2)ln|x^(1/2) + 2| + C
= (1/2)ln(x^(1/2)) + (1/2)ln(x^(1/2) + 2) + C
= ln(√x) + (1/2)ln(√x + 2) + C
Taking the limit as x approaches ∞, the integral becomes:
lim┬(b→∞)〖ln(√x) + (1/2)ln(√x + 2) 〗
= ∞
Since the integral ∫ 1 to ∞ 1/√(x(√x + 1)) dx diverges, by the integral test, the series Σ n=1 [infinity] 1/√(n(√n + 1)) also diverges.
Therefore, the correct answer is (b) diverges by the ratio test.
Learn more about ratio test at https://brainly.com/question/32619343
#SPJ11
What are the properties of determinants problems?
Answers
Properties of determinants are Reflection Property, Reliable scales Property, Scalar Multiple Property, Switching Property and All-zero Property.
1. Reflection Property: The determinant remains unchanged when its columns turn into rows and vice versa. The reflection property is what is used to describe this.
2. If every element in a row (or column) is zero, the determinant is zero, according to the all-zero property.
3. Reliable scales (Repetition) Property: If every element in a row or column is proportional to or identical to every element in another row, the determinant is zero (or column).
4. When any two of the determinant's rows (or columns) are exchanged, the sign of the determinant changes.
5. Scalar Multiple Property: If all of a determinant's components in a row (or column) are multiplied by a non-zero constant, the determinant is multiplied by that constant.
6. Factor Property: If a determinant Δ becomes zero when we put x = α, then (x – α) is a factor of Δ.
Hence this is all about determinants problems.
Learn more about Determinants problems:
https://brainly.com/question/30576580
#SPJ4
What is the shape of 7?
Answers
A seven-sided polygon is called a heptagon. A polygon with seven sides, seven angles, and seven edges is referred to as a heptagon. A heptagon's total number of angles comes to 900°.
It is also occasionally referred to as a septagon, though this usage is not advised because it combines the Latin prefix sept- (derived from septua-, meaning "seven") with the Greek suffix -gon (from gonia, meaning "angle").
A heptagon can be drawn using fourteen diagonals. Heptagon is also referred to as septagon on occasion. The Greek terms "heptá," which means "seven," and "gna," which means "angle," are combined to form the English word "heptagon. There are seven vertices, seven angles, and seven sides to it. A heptagon's internal angles add up to 900°.
Learn more about shape visit: brainly.com/question/25965491
#SPJ4
A flower pot is approximately in the shape off a cylinder. The diameter is 10 inches and the height is 6 inches. Find the surface area off the flower pot round to the nearest inch
Answers
The surface area of the cylindrical flower pot to the nearest inch is equal to \(346\;in^2\)
Given the following data:
Diameter = 10 inches.
Height = 6 inches.
Radius = \(\frac{diameter}{2} =\frac{10}{2}\) = 5 inches.
How to calculate surface area.Mathematically, the surface area (SA) of a cylinder is given by this formula:
\(S.A = 2\pi rh + 2\pi r^2\)
Where:
h is the height.r is the radius.Substituting the given parameters into the formula, we have;
\(S.A = 2\pi (5)(6) + 2\pi (5)^2\\\\S.A =188.52+157.1 \\\\S.A = 345.62\\\\S.A=346\;in^2\)
Read more on surface area here: brainly.com/question/21367171
How do you solve this?

Answers
Step-by-step explanation:
We need to find the demand so the variable x is unknown.
We know that the variable p is 37.55 so we replace that in the equation
\(37.55 = 40 - \sqrt{0.01x + 1} \)
Subtract Property
\( - 2.45 = - \sqrt{0.01x + 1} \)
Division Property
\(2.45 = \sqrt{0.01x + 1} \)
\((2.45) {}^{2} = 0.01x + 1\)
\(6.0025 = 0.01x + 1\)
\(5.0025 = 0.01x\)
\(500.25 = x\)
So the answer is about 500 units per day
What is the formula for calculating the slope m of a line?
Answers
The formula or equation used to determine the slope of a straight line is as follows:
m = (Y₂-Y₁)/(X₂-X₁)
What is an equation?An equation is about two expressions, either arithmetic or algebraic, that are related with a "=" sign that indicates equality of expressions.
Equations can be graphed, they are used to model many problems and theories.
The straight lines are characterized by a finite succession of points, when they have an inclination they adopt a slope value different from 0, and to determine that slope it is necessary to know two points of the line and use the following equation:
m = (Y₂-Y₁)/(X₂-X₁)
Where the points are:
P₁ = (X₁,Y₁)P₂ = (X₂,Y₂)Learn more about equations at:
brainly.com/question/8806877
#SPJ4

assume you've made a relative-frequency distribution graph of the above returns, which you believe enables this data to be approximated with (modeled by) a normal density function. to use this normal density function to model future spsm returns, which big assumption is most important?
Answers
It appears that you have created a relative-frequency distribution graph for some data (possibly related to investment returns) and would like to use a normal density function to model future returns. The most important assumption to consider in this context is the assumption of normality.
The normality assumption states that the underlying data follows a normal distribution, also known as the Gaussian distribution or bell curve. This distribution is characterized by its symmetric bell shape and is defined by its mean (average) and standard deviation (a measure of variability). In a normal distribution, about 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
When using the normal density function to model future returns, it is crucial to assume that the data exhibits normality. This means that the relative frequencies of the returns in the dataset follow the pattern expected from a normal distribution. If the data significantly deviates from normality, the predictions made using the normal density function might not be accurate and could lead to poor decision-making in future investment scenarios.
In summary, the most important assumption to consider when using a normal density function to model future returns based on a relative-frequency distribution graph is that the data follows a normal distribution. This assumption allows for accurate predictions and better decision-making in investment planning.
Learn more about distribution here:
https://brainly.com/question/29664127
#SPJ11
Use the formula for the area of a circle to solve for the radius of the circle if the area is 78.5cm^2
Answers
Answer:
\(r=\frac{\sqrt{314\pi}}{2\pi}\)
Step-by-step explanation:
\(A=\pi r^2 \\ \\ 78.5=\pi r^2 \\ \\ r^2=\frac{78.5}{\pi} \\ \\ r=\frac{\sqrt{314\pi}}{2\pi}\)
ILL BRAINLIEST YOU IF YOU GET IT RIGHT
Which diagram shows a pair of angle measure that proves lines c and d are parallel?

Answers
Answer:
C
Step-by-step explanation:
At first glance, it seems like all the answers work. But some careful thinking allows us to find the correct answer.
For this question, we will be using the process of elimination.
First, we can eliminate D, because it does not provide any angles on line d, so we cannot prove that line c is parallel to line d.
Second, we can eliminate A. It seems that the 2 angles makes it so that lines c and d must be parallel, however, that is only true if lines a and b are parallel. Since we don't know whether or not lines a and b are parallel, we cannot prove that lines c and d are parallel, so we can eliminate this choice.
Third, we can eliminate B. Like the diagram in A, this diagram can only prove lines c and d are parallel if lines a and b are parallel, and since we don't know whether or not lines a and b are parallel, we cannot prove tat lines c and d are parallel, so we can eliminate this choice.
We are left with C, so the answer must be C.
Of course, just to make sure, we will also check diagram C. Because the 2 angles provided in the diagram are on line a and none are on line b, we do not need line a to be related to line b in any way, as such we can pretend that line b does not exist in this diagram. We can then see that lines c and d must be parallel for this diagram, or else the angles would not work, so C is correct.
Two angles whose sum is 180° are called supplementary angles. The correct option is C.
What are supplementary angles?Two angles whose sum is 180° are called supplementary angles. If a straight line is intersected by a line, then there are two angles form on each of the sides of the considered straight line. Those two-two angles are two pairs of supplementary angles. That means, that if supplementary angles are aligned adjacent to each other, their exterior sides will make a straight line.
When two parallel lines are cut by a transverse. The angles formed on the exterior of the parallel lines are known as the Exterior Angle.
Now, For two lines two be parallel in the given diagram the measure of the angle the exterior angle on the same side of the transverse should be supplementary to each other.
The diagram shows a pair of angle measure that proves lines c and d are parallel in option c. This is because lines c and d are parallel and a is transversal to the two lines. And the measure of the exterior angles formed on the same side of the transversal is supplementary.
Hence, the correct option is C.
Learn more about Supplementary angle here:
https://brainly.com/question/2882938
#SPJ2
Please help! I will mark as brainliest IF answer is right. <3

Answers
Answer:
x- (-2,0)
Y-(0,-6)
Step-by-step explanation:
set y = to zero and solve for x
then set x= 0 and solve for y
y=-3x-6
0=-3x-6
6=-3x
-2=x
points of x intercept (-2,0)
y=-3(0)-6
y=-6
points of the y intercept
(0,-6)
At the U.S. Open Tennis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player was 100 miles per hour (mph) and the standard deviation of the serve speeds was 12 mph. Assume that the statistician also gave us the information that the distribution of the serve speeds was mound-shaped and symmetric. What proportion of the player's serves was between 110 mph and132 mph
Answers
The proportion of the player's serves between 110 mph and 132 mph is 0.1992
Given that the mean serve speed of a particular player was 100 miles per hour (mph) and the standard deviation of the serve speeds was 12 mph. Also, the distribution of the serve speeds was mound-shaped and symmetric.
To find out the proportion of the player's serves was between 110 mph and 132 mph, we need to standardize the given range to z-scores as shown below:
First, we find the z-score for the lower limit:z1 = (110 - 100)/12 = 0.83 (approx.)
Then, we find the z-score for the upper limit:z2 = (132 - 100)/12 = 2.67 (approx.)
Now, using the standard normal table, we find the area between these two z-scores as shown below:
Z-Score Table. We get the area between these two z-scores as 0.4959 - 0.2967 = 0.1992 (approx.)Therefore, the proportion of the player's serves between 110 mph and 132 mph is 0.1992 (approx.).
Know more about Z-Score Table here:
https://brainly.com/question/30766028
#SPJ11
A bus traveled on a straight road for 3 h at an average speed that was 12 mph faster than its average speed on a winding road. The time spent on the winding road was 3 h. Find the average speed on the winding road if the total trip was 210 mi.
Answers
The average speed on the winding road was 45 mph.
The bus traveled for 3 hours on the winding road, so the distance covered can be calculated using the formula: Distance = Speed × Time. Let's assume the average speed on the winding road as 'x' mph. Therefore, the distance covered on the winding road is 3x miles.
On the straight road, the bus traveled for 3 hours at an average speed that was 12 mph faster than its average speed on the winding road. So the average speed on the straight road can be expressed as 'x + 12' mph. The distance covered on the straight road can be calculated as 3(x + 12) miles.
The total distance covered in the entire trip is given as 210 miles. Therefore, we can write the equation:
3x + 3(x + 12) = 210
Simplifying the equation:
3x + 3x + 36 = 210
6x + 36 = 210
6x = 174
x = 29
So the average speed on the winding road was 29 mph.
The problem states that the bus traveled for 3 hours on both the winding road and the straight road. Let's assume the average speed on the winding road as 'x' mph. Since the bus traveled for 3 hours on the winding road, the distance covered can be calculated as 3x miles.
On the straight road, the average speed was 12 mph faster than on the winding road. Therefore, the average speed on the straight road can be expressed as 'x + 12' mph. The distance covered on the straight road can be calculated as 3(x + 12) miles.
The total distance covered in the entire trip is given as 210 miles. This allows us to set up the equation 3x + 3(x + 12) = 210 to solve for 'x'. Simplifying the equation leads to 6x + 36 = 210. Solving for 'x', we find that the average speed on the winding road was 29 mph.
In summary, the average speed on the winding road was 29 mph.
Learn more about distance
brainly.com/question/13034462
#SPJ11