johanna prepares a mixture of salad mixed with mayonnaise carrots cucumber lettuce and cheese. what type of mixture divine salad is? why do you think so?
Answers
Answer:
johanna prepares a mixture of salad mixed with mayonnaise carrots cucumber lettuce and cheese. what type of mixture divine salad is? why do you think so
Related Questions
The daily water consumption for an Ohio community is normally distributed with a mean consumption of 519,645 gallons and a standard deviation of 71,564 gallons. The community water system will experience a noticeable drop in water pressure when the daily water consumption exceeds 782,238 gallons. What is the probability of experiencing such a drop in water pressure
Answers
Answer:
0.0001
Step-by-step explanation:
The computation of the probability of experiencing such a drop in water pressure is shown below:
Given that
mean = 519,645 gallons
Standard deviation = 71,564 gallons
Now the probability is
= 1 - p (x - mean ÷ standard deviation < 782,238 - 519,645 ÷ 71,564)
= 1 - p(z<3.67)
= 1 - 0.9999
= 0.0001
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form.
If you are using a screen-reader, please consult your instructor for assistance.
x=
y=
Answers
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$. Therefore $x=y=12\sqrt{3}$, which is our answer
In a 30-60-90 triangle, the sides have the ratio of $1: \sqrt{3}: 2$. Let's apply this to solve for the variables in the given problem.
Instructions: Use the ratio of a 30-60-90 triangle to solve for the variables. Leave your answers as radicals in simplest form. x=y=Let's first find the ratio of the sides in a 30-60-90 triangle.
Since the hypotenuse is always twice as long as the shorter leg, we can let $x$ be the shorter leg and $2x$ be the hypotenuse.
Thus, we have: Shorter leg: $x$Opposite the $60^{\circ}$ angle: $x\sqrt{3}$ Hypotenuse: $2x$
Now, let's apply this ratio to solve for the variables in the given problem. We know that $x = y$ since they are equal in the problem.
Using the ratio of the sides, we have:$x\sqrt{3} = 12\sqrt{3}$ (opposite the $60^{\circ}$ angle is 12$\sqrt{3}$)$x = 2\sqrt{3}\cdot6$ (the hypotenuse is $2x = 12\sqrt{3}$)Simplifying, we have:$x = 12\sqrt{3}$
Therefore, $x=y=12\sqrt{3}$, which is our answer.
For more such questions on ratio of the sides
https://brainly.com/question/31529028
#SPJ8
plz help!!!!, need this if anyone can help!!!!!!!! No links plz

Answers
Answer:
-5 * ln 0.5 or around 3.466
Step-by-step explanation:
first divide both sides by 2800 to get 0.5=\(e^{-0.2x}\). next put this in natural log: ln 0.5 = -0.2x divide both sides by -0.2 to get x = -5ln 0.5
what is the slopeof the function x=(-4) y=(-2)
Answers
Answer: The answer is -4. Hope this helps!
Assume that the readings at freezing on a batch of thermometers are normally distributed with a mean of 0°C and a standard deviation of 1.00°C. A single thermometer is randomly selected and tested.
If 2.5% of the thermometers are rejected because they have readings that are too high and another 2.5% are rejected because they have readings that are too low, find the two readings that are cutoff values separating the rejected thermometers from the others.
Answers
Using the normal distribution, it is found that the two readings that are cutoff values separating the rejected thermometers from the others are -1.96ºC and 1.96ºC.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable with mean \(\mu\) and standard deviation \(\sigma\) is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure is above or below the mean. Looking at the z-score table, the p-value associated with this z-score is found, which is the percentile of X.The mean and the standard deviation are given, respectively, by:
\(\mu = 0, \sigma = 1\).
The z-score that cuts off the bottom and top 2.5% of the distribution is \(z = \pm 1.96\), hence:
\(Z = \frac{X - \mu}{\sigma}\)
\(-1.96 = \frac{X - 0}{1}\)
X = -1.96
\(Z = \frac{X - \mu}{\sigma}\)
\(1.96 = \frac{X - 0}{1}\)
X = 1.96
The two readings that are cutoff values separating the rejected thermometers from the others are -1.96ºC and 1.96ºC.
More can be learned about the normal distribution at https://brainly.com/question/27879230
#SPJ1
Help me find the answer please

Answers
Answer:
60
Step-by-step explanation:
m∠1=(55+65)/2=60
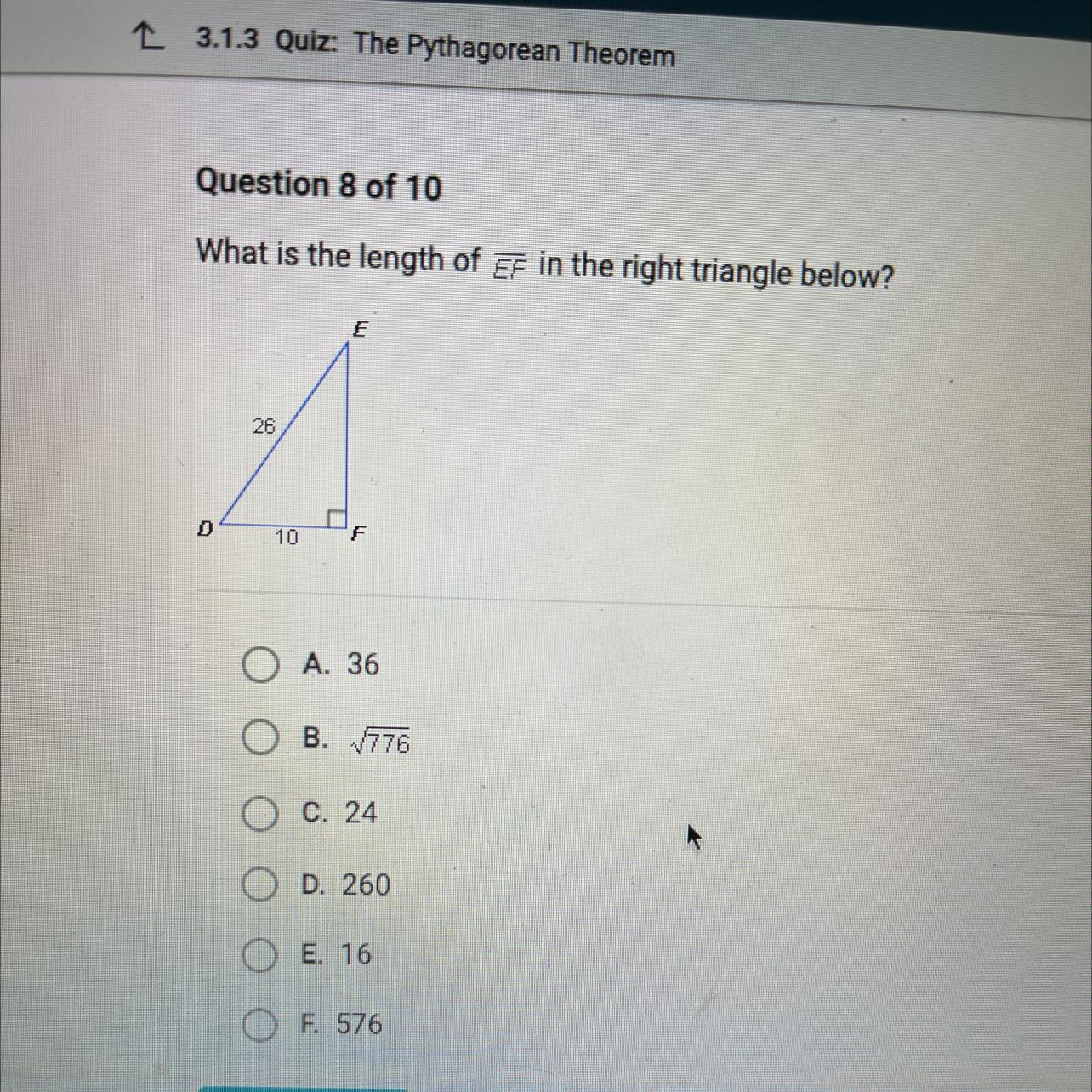
What is the length of EF in the right triangle below?
D
26
10
E
F
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
Kai and Finley were studying together for their exams the
following day. They had planned to spend the entire two days
after the exams hiking to a log cabin on the Winslow trail. The trail
was closed on Mondays, Wednesdays, and weekends.
On which day of the week was their exam scheduled?
Answers
Their exam must have been scheduled on Wednesday, allowing them to start hiking on Thursday after the exams.
How to determine which day of the week was their exam scheduledTo determine the day of the week on which Kai and Finley's exam was scheduled, we need to consider the information provided about the trail being closed on Mondays, Wednesdays, and weekends.
If they had planned to hike to the log cabin for two days after the exams, and the trail is closed on weekends, it means they cannot start hiking on Saturday or Sunday.
Since they cannot start hiking on Saturday or Sunday, the two possible options for the exam day would be Monday or Wednesday, as they have not specified whether the hike starts immediately after the exams or the day after.
However, we can conclude that their exam was not scheduled on Monday, as the trail is closed on Mondays, and they had planned to hike immediately after the exams.
Therefore, their exam must have been scheduled on Wednesday, allowing them to start hiking on Thursday after the exams.
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
A small school has 78 students. If 24 of the students are boys, what is the ratio of girls to boys?
Answers
Answer:
a
Step-by-step explanation:
Answer:
54 girls
Step-by-step explanation:
6. The fixed costs of producing a Wild Widget are $34,000. The variable costs are $5.00 per widget. What is the average cost per widget of producing 7,000 Wild Widgets? Round to the nearest cent. :))))
Answers
Answer: To calculate the average cost per widget, we need to consider both the fixed costs and the variable costs.
Fixed costs: $34,000
Variable costs per widget: $5.00
Total costs = Fixed costs + (Variable costs per widget × Number of widgets)
Total costs = $34,000 + ($5.00 × 7,000)
Total costs = $34,000 + $35,000
Total costs = $69,000
Average cost per widget = Total costs / Number of widgets
Average cost per widget = $69,000 / 7,000
Average cost per widget ≈ $9.86
Therefore, the average cost per widget of producing 7,000 Wild Widgets is approximately $9.86.
Step-by-step explanation: :)
a store is having a sale on trail mix and jelly beans. for 3 pounds of trail mix and 5 pounds of jelly beans the total cost is $21. for 6 pounds of trail mix and 2 pounds of jelly beans. the total cost $24 find the cost for each pound of trail mix and each pound of jelly beans
Answers
The trail mix costs $1.25 / pound
Solve the following inequality algebraically. ∣x−5∣≤11
Answers
Answer:
\(-6\leq x\leq 16\)
Step-by-step explanation:
So we have the inequality:
\(|x-5|\leq 11\)
Definition of Absolute Value:
\(x-5\leq 11\text{ or } x-5\geq -11\)
Note that the sign is flipped in the second case because we multiplied by a negative.
Add 5 to both sides to both equations:
\(x\leq 16\text{ or } x\geq -6\)
Merge:
\(-6\leq x\leq 16\)
And we're done!
A triangle has a base length of 3ac2 and a height 2 centimeters more than the base length. Find the area of the triangle if a = 2 and c = 3.
Answers
The area of the triangle, when a = 2 and c = 3, is 1512 square centimeters.
We must apply the formula for the area of a triangle, which is provided by: to determine the triangle's area.
(1/2) * Base * Height = Area
We can enter the values of a = 2 and c = 3 into the formula given that the base length is 3ac2 and the height is 2 centimetres greater than the base length.
Base length =\(3ac^2 = 3 * 2 * (3^2) = 3 * 2 * 9 = 54\) centimeters
Height is calculated as Base Length + 2 (54 + 2 = 56 centimetres).
Using these values as a substitute in the formula, we obtain:
Area =\((1/2) * 54 * 56 = 1512\) square centimeters
centimetres square
It's crucial to understand that the calculation assumes the triangle is a right triangle with the specified base and height and that the given values of a and c are accurately used in the formula.
for more such questions on triangle
https://brainly.com/question/25215131
#SPJ8
Two cars leave the same point at the same time travelling in opposite directions. one car travels west at 20 mph and the other travels east at 60 mph. In how many hours will they be 280 miles apart?
Answers
It will take 3.5 hours for the two cars to be 280 miles apart.
To determine the time it takes for the two cars to be 280 miles apart, we can use the concept of relative velocity.
Since the cars are traveling in opposite directions, their velocities can be added together to find their relative velocity:
Relative velocity = Velocity of car traveling east + Velocity of car traveling west
Relative velocity = 60 mph + 20 mph
Relative velocity = 80 mph
The relative velocity of the cars is 80 mph, which means that they are moving away from each other at a combined speed of 80 mph.
To find the time it takes for them to be 280 miles apart, we can use the formula:
Time = Distance / Speed
Plugging in the values, we have:
Time = 280 miles / 80 mph
Time = 3.5 hours
Therefore, it will take 3.5 hours for the two cars to be 280 miles apart.
During this time, the car traveling east would have covered a distance of 60 mph × 3.5 hours = 210 miles, while the car traveling west would have covered a distance of 20 mph × 3.5 hours = 70 miles.
The sum of these distances is indeed 280 miles, confirming the result.
For more questions on relative velocity.
https://brainly.com/question/11418015
#SPJ8
Assuming that the equations define x and y implicitly as differentiable functions x = f(t), y=g(t), find the slope of the curve x = f(t), y = g(t) at the given value of t.
x=t^5 + t, y + 3t^5 = 3, x + 13, t= 3 The slope of the curve at t= 3 is
Answers
To find the slope of the curve at t=3, we first need to find the values of x and y at t=3 using the given equations.
x = (3)^5 + 3 = 246
y + 3(3)^5 = 3
y = -1347
Next, we can differentiate both equations with respect to t to get the following:
dx/dt = 5t^4 + 1
dy/dt = -15t^4
At t=3, we get
dx/dt = 5(3)^4 + 1 = 454
dy/dt = -15(3)^4 = -1215
Therefore, the slope of the curve at t=3 is given by dy/dx = (dy/dt)/(dx/dt) = (-1215/454) ≈ -2.68. This means that the curve is decreasing (sloping downwards) at t=3.
To learn more about slope of the curve:
https://brainly.com/question/30466171
#SPJ4
Question 22
The sum of two numbers is 107. The difference of the two numbers is 53. What are the two
numbers.
Let z be the larger number and y be the smaller number.
Write an equation that expresses the information in the sentence "The sum of two numbers is 107."
Write an equation that expresses the information in the sentence "The difference of the two
numbers is 53."
Solve the system you have written above.
The larger number, a is
> Next Question
The smaller number, y is

Answers
The requried larger number x is 80 and the smaller number y is 27.
Let's use the given variables:
x be the larger number
y be the smaller number
According to question
The sum of two numbers is 107 is represented by x + y = 107
The difference between the two numbers is 53 is represented by x - y = 53.
Solving the system of equations:
(x + y) + (z - y) = 107 + 53
2x = 160
x = 80
Now, z = 80, substitute this value into one of the original equations to solve for y.
x + y = 107
80 + y = 107
y = 27
Therefore, the requried larger number x is 80 and the smaller number y is 27.
Learn more about the system of equations here:
https://brainly.com/question/24065247
#SPJ1
A grid that represents 1 whole , what would you shade for 0.4 and 0.04? 100 squares in rows of 10.
Answers
A solid figure is composed of a cube and a right triangular
prism. The figure and some of its dimensions are shown in
this diagram.
- 8 cm
What is the volume of the figure?
A
6 cm
B
560 cubic centimeters
704 cubic centimeters
C 728 cubic centimeters

Answers
Answer:
Option B
Step-by-step explanation:
704 cubic centimeters
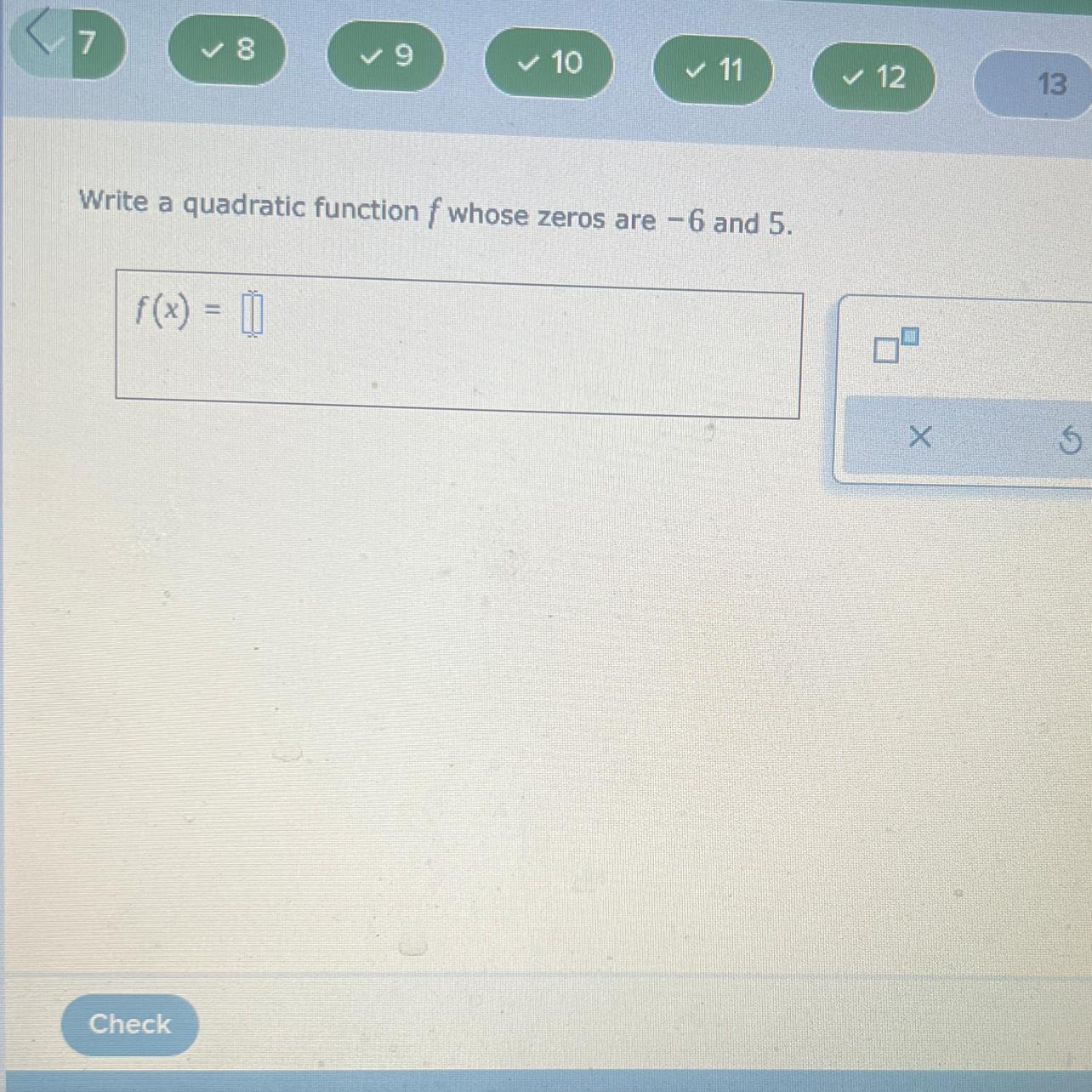
Please help this was due yesterday
Answers
Answer:
f(x) = (x +6)(x -5) or f(x) = x² +x -30
Step-by-step explanation:
You want a quadratic function whose zeros are -6 and +5.
FactorsIf p is a zero of the polynomial f(x), then (x-p) is a factor. The two given zeros meant that the factors are ...
f(x) = (x -(-6))·(x -5)
f(x) = (x +6)(x -5) . . . . . . . . simplify a bit
This can be put in standard form by multiplying the factors:
f(x) = x(x -5) +6(x -5) = x² -5x +6x -30
f(x) = x² +x -30 . . . . . . . . simplified quadratic function
The quadratic function of the zeros is f(x) = \(x^2+x-30\).
What is quadratic function?
A polynomial function that has one or more variables and a variable having a maximum exponent of two is said to be quadratic. A polynomial of degree 2 is referred to as such because the greatest degree term in a quadratic function is of second degree. There must be at least one second-degree term in a quadratic function. It is a mathematical function.
Here the zeros of the function is -6 and 5.
We know that if zeros of the function is a then the factor is (x-a).
Then,
=> f(x) = (x-(-6))(x-5)
=> f(x) = (x+6)(x-5)
=> f(x) = \(x^2+6x-5x-30\)
=> f(x) = \(x^2+x-30\)
Hence the quadradic function is f(x) = \(x^2+x-30\).
To learn more about quadradic function refer the below link
https://brainly.com/question/1214333
#SPJ1
47% of the students in a class of 34 students has glasses or contacts. How many students in the class have either glasses or contacts?
Answers
Answer:
16
Step-by-step explanation:
47% is 0.47
34 x 0.47 = 15.98
So a trick question, its either 15 students or 16 students.... I would say 16 students, although the percentage would be 47.05%
16 students either have glasses or contacts.
Emily has a decorative box that is shaped like a cube with a height of
5 inches. What is the surface area of the box?
HELP MEH ASAP PLS PLZ PLZ
Answers
Answer:
5 x 5 x 5 x 5 x 5
Step-by-step explanation:
The distances, in light years, of four stars from a space probe are shown. Put the stars in order from the closest one (least distance) to the farthest one (greatest distance). 0.886 0.883 1.25 0.89
A.
0.883, 0.886, 0.89, 1.25
B.
0.883, 0.886, 1.25, 0.89
C.
1.25, 0.89, 0.886, 0.883
D.
0.886, 0.883, 0.89, 1.25
Answers
The stars in order from the closest one to the farthest one are:
0.883, 0.886, 0.89, 1.25
so, the answer is A.
What is a sequence?
A sequence is an enumerated collection of objects in which repetitions are allowed. Like a set, it contains members (also called elements, or terms).
To put the given distances in order from the closest one to the farthest one, we need to arrange them in ascending order.
That means we need to start with the smallest value and move toward the largest value.
Looking at the given distances, we see that the smallest value is 0.883, followed by 0.886, then 0.89, and finally 1.25, which is the largest value.
Putting the given distances in ascending order, we get:
0.883, 0.886, 0.89, 1.25
Therefore, the stars in order from the closest one to the farthest one are:
0.883, 0.886, 0.89, 1.25
so, the answer is A.
To know more about sequence visit:
brainly.com/question/12246947
#SPJ1
Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help Plz help

Answers
Answer:
1. KLP + PLM = 180 degrees (straight line)
2. 3x + angle PLM = 180 degrees
3. angle PLM = 180 - 3x
4. PMN = P + PLM (Exterior angle)
5. 2x + 72 = x + 180 - 3x
6. x = 27
Step-by-step explanation:
1. Notice that angle KLP + angle PLM is a straight line, so KLP + PLM = 180 degrees (straight line)
2. angle KLP = 3x, so
3x + angle PLM = 180 degrees
3. angle PLM = 180 - 3x
4. PMN = P + PLM (Exterior angle)
5. 2x + 72 = x + 180 - 3x
6. 5 gives 4x = 108, so x = 27
Answer:
1. KLP + PLM = 180 degrees (straight line)
2. 3x + angle PLM = 180 degrees
3. angle PLM = 180 - 3x
4. PMN = P + PLM (Exterior angle)
5. 2x + 72 = x + 180 - 3x
6. x = 27
Step-by-step explanation:
ngl i didnt really get this i i kinda have a some what idea on what this is
The exterior angles of the triangle added to their corresponding interior angles equal 180 degrees by virtue of the sum of angles on a straight line.
As such the interior angles are
1. 180 - (x+ 3)
2. 180 - (2x+ 1)
3. 180 - (3x - 4)
Given that the sum of angles in a triangle is 180 degrees
180 - (x+ 3) + 180 - (2x+ 1) + 180 - (3x - 4) = 180
540 - 6x = 180
6x = 540 - 180
6x = 360
x = 60
The exterior angles are
x + 3 = 60 + 3 = 63
2x + 1 = 2(60) + 1 = 121
and
3x - 4 = 3(60) - 4 = 180 - 4 = 176
Identify the quadratic function(s). (Select all that apply.) 8 - 5x = 4(3x - 1) (4a + 2)(2a - 1) + 1 = 0 2y + 2(3y - 5) = 0 2b(b - 7) + b = 0
Answers
Answer: A quadratic function is a polynomial function of form f(x) = ax^2 + bx + c where a,b, and c are constants, and a is not equal to zero.
The given functions are:
8 - 5x = 4(3x - 1)
(4a + 2)(2a - 1) + 1 = 0
2y + 2(3y - 5) = 0
2b(b - 7) + b = 0
The quadratic function(s) among them are:
2. (4a + 2)(2a - 1) + 1 = 0
2b(b - 7) + b = 0
The first one 8 - 5x = 4(3x - 1) is linear and not a quadratic function, and the third one 2y + 2(3y - 5) = 0 is also linear, not a quadratic function.
Note that to identify a quadratic function, we can look for the pattern of x^2 or y^2 in the equation.
Also, we could expand the second degree polynomials in the form (ax^2+bx+c) and check if there are x^2 or y^2 term on both sides of the equation.
Step-by-step explanation:
HELP NEEDED ASAP
Identify the constant in the expression: 16y +2y + 3 - 2x
A. y
B. 2
C. 3
4. x

Answers
l am not sure but I think it's Y
On one day at a local minigolf course, there were 320 customers who paid a total of $2,900. If the cost for a child is $7 per game and the cost for an adult is $10 per game, write a system of equations to model this scenario, where x represents the number of children and y represents the number of adults who played that day.
7x + 10y = 2900
x + y = 320
7x + 10y = 320
x + y = 2900
10x + 7y = 2900
x + y = 320
10x + 7y = 320
x + y = 2900
Brainiest for correct answer
Answers
A system of equations to model this scenario is given as follows -
x + y = 320
7x + 10y = 2900
What is expression?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.The general equation of a straight line is → y = mx + c{m} - slope {c} - intercept along the y - axis.
Given is that on one day at a local minigolf course, there were 320 customers who paid a total of $2,900. The cost for a child is $7 per game and the cost for an adult is $10 per game.
Let {x} represents the number of children and {y} represents the number of adults who played that day. We can write the given system of equations as -
x + y = 320
7x + 10y = 2900
Therefore, a system of equations to model this scenario is
x + y = 320
7x + 10y = 2900
To solve more questions on expressing evaluation, visit the link below -
brainly.com/question/1041084
#SPJ1
Use the shell method to find the volume of the solid obtained by rotating the region bounded by the curves y=4x-2 and y=x^2+1 about the y-axis. Simplify your solution.
Answers
The volume of the solid of revolution is \(\frac{16\pi}{3}\) cubic units.
First, we determine the limits between the two curves. (\(f(x) = 4\cdot x -2\), \(g(x) = x^{2}+1\))
\(f(x) = g(x)\) (1)
\(4\cdot x - 2 = x^{2}+1\)
\(x^{2}-4\cdot x +3 = 0\)
\((x-1)\cdot (x-3) = 0\)
The lower and upper bounds are 1 and 3, respectively. It is to notice that \(f(x) > g(x)\) for \(x \in (1, 3)\). Thus, we determine the volume of the solid of revolution by shell method, that is to say:
\(V = 2\pi \int\limits^a_b {x\cdot |f(x) - g(x) |} \, dx\) (2)
If we know that \(a = 3\), \(b = 1\), \(f(x) = 4\cdot x - 2\) and \(g(x) = x^{2}+1\), then the volume of the solid of revolution is:
\(V = 2\pi \int\limits^3_1 {|4\cdot x^{2}-2\cdot x -x^{3}-x|} \, dx\)
\(V = 2\pi\int\limits^3_1 {(4\cdot x^{2}-x^{3}-3\cdot x)} \, dx\)
\(V = 8\pi \int\limits^3_1 {x^{2}} \, dx - 2\pi \int\limits^3_1 {x^{3}} \, dx -6\pi \int\limits^3_1 {x} \, dx\)
\(V = 8\pi\cdot \left(\frac{3^{3}}{3}-\frac{1^{3}}{3} \right)-2\pi \cdot \left(\frac{3^{4}}{4}-\frac{1^{4}}{4} \right) - 6\pi\cdot \left(\frac{3^{2}}{2}-\frac{1^{2}}{2} \right)\)
\(V = \frac{208\pi}{3} - 40\pi -24\pi\)
\(V = \frac{16\pi}{3}\)
The volume of the solid of revolution is \(\frac{16\pi}{3}\) cubic units.
To learn more on solids of revolution, we kindly invite to check this verified question: https://brainly.com/question/338504
f(x)
= x² + 3x -
-
f(6) = [?]
Be sure to simplify your answer.
XIN
![f(x)= x + 3x --f(6) = [?]Be sure to simplify your answer.XIN](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fU5ONjlwDEZB2nbAqiKc29GZ0d97SG1K.png)
Answers
Answer:
f(6) = 51
Step-by-step explanation:
f(x)= x² + 3x - x/2
In order to find f(6) ,we need to substitute
x by 6 in the expression of f :
f(6) = (6)² + 3(6) - (6)/2
= 36 + 18 - 3
= 54 - 3
= 51
Then
f(6) = 51
Answer:
f(6) = 51
Step-by-step explanation:
Simplify:
Substitute the value of x
\(\sf f(x) =x^2 + 3x -\dfrac{x}{2}\\\\f(6)=6^2 + 3*6 -\dfrac{6}{2}\\\\\)
= 36 + 18 - 3
= 51
Ajar contains nickels and dimes. There is a
total of 200 coins in the jar and their value is
$14.55. How many dimes are in the jar?
Answers
Answer:
There are 91 dimes in the jar.
Step-by-step explanation:
5n+10d= 1455
n+d = 200
n=200-d
5(200-d) + 10d=1455
1000-5d+10d=1455
1000+5d=1455
5d=455
d=91
91 dimes
How much does the airplane weigh if it is carrying 66 gallons of fuel? PLEASE ANSWER WITH CORRECT ANSWER PICTURE INCLUDED

Answers
The weight of the plane when there is 66 gallons of fuel in it is 2,529 lb.
What is the weight of the plane?A linear function is a function that when drawn on a coordinate plane, it is a straight line. A linear function is made up of a single variable that is raised to the power of one.
If the weight of the plane is a linear function, it means that the weight of the plane increases at a constant rate.
The first step is to determine the rate of increase in the weight of the plane: (2451 - 2230) / (54 - 20) = 6.5 lb
The second step is to determine the weight of the plane when there is no fuel in it:
2451 - (6.5 x 54) = 2100 lb
Weight of the plane when there is 66 gallons of fuel in it : 2100 + (6.5 x 66) = 2,529 lb
To learn more about linear functions, please check: https://brainly.com/question/26434260
#SPJ1