Jose paid 45.00$ for 5 movie tickets . EACH ticket cost the same amount . What was the cost of each movie ticket in dollars ?
Answers
Answer:
$9
Step-by-step explanation:
divide 45 and 5, you get 9
Answer:
45.00$ divided by 5.00$ is 9.00$
i hoped this helped!
Step-by-step explanation:
Related Questions
Answer this question Use the Second Derivative Midpoint Formula formula to approximate f'(0.6) for the table data points given that h = 0.06.
Select the correct answer
A. 2376.342000000
B. 594.085500000
C. 2079.299250000
D. 1782.256500000
E. 297.042750000
Answers
To approximate f'(0.6) using the Second Derivative Midpoint Formula with the given table data points and h = 0.06, follow these steps:
1. Identify the relevant data points: f(0.54), f(0.6), and f(0.66).
2. Apply the Second Derivative Midpoint Formula: f'(0.6) ≈ (f(0.66) - 2f(0.6) + f(0.54)) / (h^2).
Unfortunately, I cannot provide a specific answer without the values for f(0.54), f(0.6), and f(0.66).
Please provide these values, and I will gladly help you complete the calculation.
Learn more about Second Derivative Midpoint Formula: https://brainly.com/question/30747891
#SPJ11
Let A and B be a (2x2) matrices such that A^2 = AB and A /= 0. Find the flaw in the following proof that A = B : Since A^2 = AB, A^2 - AB = 0 Factoring yields A(A-B) = 0. Since A /- 0, it follows that A-B = 0. There A =B.
Answers
The flaw in the proof is that it assumes that if A(A-B) = 0 and A is not equal to zero, then A-B must be equal to zero. However, this is not necessarily true for matrices.
Here is a counterexample:
Let A =
| 2 0 |
| 0 0 |
and B =
| 1 0 |
| 0 0 |
Then A^2 =
| 4 0 |
| 0 0 |
and AB =
| 2 0 |
| 0 0 |
So A^2 - AB =
| 2 0 |
| 0 0 |
Multiplying by A^-1 on the left (since A is not equal to zero, it is invertible) gives:
A(A-B) =
| 2 0 |
| 0 0 |
So A(A-B) = 0. However, A-B =
| 1 0 |
| 0 0 |
which is not equal to zero. Therefore, the assumption that A-B = 0 does not hold, and the proof is invalid.
In conclusion, the fact that A(A-B) = 0 does not imply that A-B = 0 for matrices. Therefore, we cannot conclude that A = B based on the given information.
To know more about matrices refer here:
https://brainly.com/question/30646566#
#SPJ11
WILL GIVE BRAINLIEST IMMEDIATELY!!! INSTANT BRAINLIEST!!!!!!!1
I ONLY NEED STATEMENT 7's REASON!!! SEE PHOTO
PUT ANSWER TO STATEMENT 7:
it is either SSS, SAS, ASA, or AAS
5. Consider the figure below.
Given: Parallelogram SUPN, SR ⊥ UN and MP ⊥ UN
Prove: ΔPMU ≅ ΔSRN

Answers
Answer: Lol, do your homework.
Answer:
SAS
Well I took geometry last year so I don't know how to explain it well but when you move from each Angle/Point it wouldn't make sense for it to be SSS, or AAS, or any other one since there is only one given angle which is 90 degrees and its in between the sides.
derivative of 1/(1+e^-x)
Answers
Answer:
hope this helps.
Step-by-step explanation:

The perm pattern that includes a central rectangle and two sections at each side is the:
a) rectangle pattern
b) contour pattern
c) spiral bricklay pattern
d) alternating oblong pattern
Answers
The perm pattern that includes a central rectangle and two sections at each side is the contour pattern.
The contour pattern in a perm involves dividing the hair into three sections, with a rectangular section in the center and two additional sections on each side. The hair is then wrapped around perm rods in a pattern that follows the contour of the head. This pattern is often used to create natural-looking waves or curls.
The other patterns listed - rectangle pattern, spiral bricklay pattern, and alternating oblong pattern - are not typically used in perming hair.
Learn more about rectangle here:
https://brainly.com/question/15019502
#SPJ11
help me pls!! i rlly need it!!
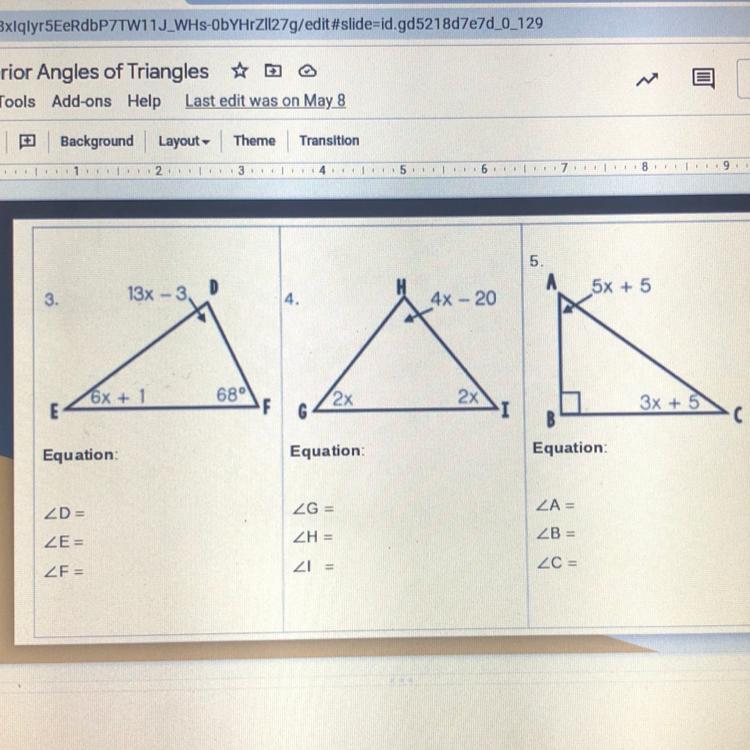
Answers
Answer:
3. below
<D = 75°
<E = 37°
<F = 68°
4. below
<G = 50°
<H = 80°
<I = 50°
5. below
<A = 55°
<B = 90°
<C = 35°
Step-by-step explanation:
In a triangle, all angles add up to 180°, so we can set up equation accordingly:
3. m<E + m<F + m<D = 180°
6x + 1 + 68 + 13x - 3 = 180
19x + 66 = 180
19x = 114
x = 6°
We can substitute the value of x back into the expressions for each angle:
m<E = 6x + 1 = 6(6) +1 = 36 + 1 = 37°
m<F = 68°
m<D = 13x - 3 = 13(6) - 3 = 75°
4. m<G + m<I + m<H = 180°
2x + 2x + 4x - 20 = 180
8x - 20 = 180
8x = 200
x = 25°
We can substitute the value of x back into the expressions for each angle:
<G = 2x = 50°
<H = 4x - 20 = 4(25) - 20 = 80°
<I = 2x = 50°
5. m<B + m<C + m<A = 180°
90 + 3x + 5 + 5x + 5 = 180
100 + 8x = 180
8x = 80
x = 10°
We can substitute the value of x back into the expressions for each angle:
<A = 5x + 5 = 5(10) + 5 = 55°
<B = 90°
<C = 3x + 5 = 3(10) + 5 = 35°
What is the approximate distance between points (-5,-1) and point M (7,6)?
A. 19.3units
B. 96.5units
C. 7 units
D. 13.9 units
Answers
HELLLPPPPP
45 POINTS!!!!!!
Calculate the percent increase or decrease between the starting and ending quantities below. Round your answer to one decimal place. (There’s 5 questions to answer)
1- Start:3 end: 10
2- start:9 end:20
3-start:100 end: 85
4- start: 45 end:20
5-start: 30 end: 60
Answers
1 - there will be increase of 233.33 % , 2 - there will be increase of 122.22 % , 3 - there will be decrease of 15 % , 4 - there will be decrease of 55.56 % , 5 - there will be increase of 100%
WHAT IS PERCENTAGE ?% is a relative number that is used to represent hundredths of any quantity. Since one percent (1%) equals one tenth of something, 100 percent denotes the entire amount, and 200 percent denotes twice the amount mentioned percentage.
CALCULATION1 - Start : 3 end : 10
formula for finding percentage increase is = \(\frac{end - start }{start } * 100\)
so substituting value in the formula ;
that is equal to = \(\frac{10-3}{3} * 100\)
= \(\frac{7}{3} * 100\)
= 233.33% increase
2 - Start : 9 End : 20
directly substituting the values in the above mentioned formula
= \(\frac{20-9}{9} * 100\)
= \(\frac{11}{9} * 100\)
= 122.22% increase
3 - Start : 100 end : 85
plugging in the values = \(\frac{85-100}{100}*100\)
= \(\frac{-15}{100} * 100\)
= -15% i.e. decrease of 15%
4 - Start : 45 end : 20
putting in the values = \(\frac{20-45}{45} * 100\)
= \(\frac{-25}{45}*100\)
= -55.56% i.e. decrease of 55.56 %
5 - Start : 30 end : 60
putting in the values = \(\frac{60-30}{30}* 100\)
= \(\frac{30}{30} * 100\)
= 100% increase
learn more about the percentage here :
brainly.com/question/16797504
#SPJ9
Find equations of the tangents to the curve x = 3t^2 + 1, y = 2t^3 + 1 that pass through the point (4,3).
Answers
The slopes of the tangents at the points (1, 1) and (-5, 3) . Hence, the equations of the tangents are y = 2x - 1 and 13x + 9y - 78 = 0.
Given, x = 3t² + 1, y = 2t³ + 1The point through which the tangents pass is (4, 3).Let the point of contact be (h, k).
Then the slope of the tangent at that point is,dy/dx = (dy/dt)/(dx/dt)Also, the tangent passes through (4, 3).
So, we have:3t² + 1 = 4 .......(1)2t³ + 1 = 3 ........(2)Solving (1) and (2), we get,t = 1, -1
Substituting these values in (1) and (2), we get the points of contact:(4, 3) is the given point. So, we can use (1, 1) and (-5, 3) as the points of contact.
So the slopes of the tangents at the points (1, 1) and (-5, 3) are given by:dy/dx = (dy/dt)/(dx/dt) at (1, 1)
=> 18/9 = 2dy/dx = (dy/dt)/(dx/dt) at (-5, 3)
=> 78/(-54) = -13/9
The equations of the tangents are: y - 1 = 2(x - 1) => y = 2x - 1 and y - 3 = (-13/9)(x + 5) => 13x + 9y - 78 = 0
Hence, the equations of the tangents are y = 2x - 1 and 13x + 9y - 78 = 0.
Learn more about tangents here:
https://brainly.com/question/10053881
#SPJ11
Give the value of M and C.

Answers
Answer:
y = 5x - 3, so M = 5 and C = -3.
This is a math question I’m not really familiar with. Harry receives 30% commission on the appliances he sells. If he sells a TV for $350, a refrigerator for $400 and a heater for $440, how much does Harry make in commission?
Answers
Answer:
the answer is 357
Step-by-step explanation:
350 + 440 + 400 = 1190
30% of 1190 = 357
May I have brainliest please? :)
to work out the distance travelled between 2 places, use the word formula:
distance = speed × time
find the distance travelled for the following journey
150km/h for 2 hours
Answers
Answer:
Step-by-step explanation: Using the formula:
distance = speed × time
where speed is in km/h and time is in hours
We have:
distance = 150 km/h × 2 h = 300 km
Therefore, the distance travelled for the journey is 300 km.
if f(x)=x23 is an antiderivative of f(x), find ∫(4f(x)−5x3)dx.
Answers
The integral of \((4f(x) - 5x^3)\) dx is equal to\(2x^24 - (5/4)x^4 + C\), where C is the constant of integration.
Given that f(x) =x^23 is an antiderivative of f(x), we can find the integral of (4f(x) - 5x^3) dx as follows:
∫(4f(x) - \(5x^3\))dx
= ∫4(x^23 ) dx - ∫5(\(x^3\)) dx [using linearity of integration]
= 4∫(x^23) dx - 5∫ (\(x^3\)) dx
= 4(2x^24/4 + C1) - 5(\(x^4/4\) + C2) [using the power rule of integration]
= 2x^24 - \((5/4)x^4\) + C, where C = 4C1 - 5C2 is the constant of integration.
Therefore, the antiderivative of (4f(x) - \(5x^3)\) is 2x^24 - \((5/4)x^4\) + C. This means that if we differentiate 2x^24 -\((5/4)x^4\) + C with respect to x, we will get (4f(x) -\(5x^3\)). The constant of integration, C, is not uniquely determined by the given integral, and its value depends on the initial conditions of the problem.
Learn more about antiderivative here:
https://brainly.com/question/28208942
#SPJ11
Question 3 (5 points) Convert the decimal 0.929292... to a fraction.
Answers
Answer:
92 over 100
Step-by-step explanation:
Alfred and rani both picked different two-digit numbers. If you multiply alfred’s number by 5 and double rani’s number, the sum is 300. If you double alfred’s number and multiply rani’s number by 3, the sum of the two numbers is 252. What is the sum of their two numbers?.
Answers
In linear equation, 96 is the sum of their two numbers .
What are a definition and an example of a linear equation?
An equation in which there is only one variable is known as a linear equation in one variable.It has the mathematical formula Ax + B = 0, where A and B can be any two real numbers, and x is an unknowable variable with just one possible value.One such linear equation in one variable is 9x + 78 = 18.Let Alfred take x and Rani take y.
As per given question,
5x + 2y = 300 .............1
2x + 3y = 252 ..............2
On multiplying (1) with 3 and equation (2) with 2, we get
15x + 6y = 900
4x + 6 y = 504
On subtracting both, we get
15x + 6y = 900
4x + 6y = 504
______________________
11x = 396
x = 36
Putting x = 36 in (1), we get
5 * 36 + 2y = 300
2y = 300 - 180
2y = 120
y = 120/2
y = 60
Sum of two numbers is 60 + 36 = 96
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
solving systems of equations in three variables

Answers
Answer:
A: (x = 34, y = -27, z = -1)
Step-by-step explanation:
Plug the variables in. It might be tedious, but it guarantees you get it right.
Let's try A first. 2(34) + 2(-27) + 6(-1) = 8. Is this correct? Yes. However, you gotta plug it in for the other three equations. 5(34) + 6(-27) + 5(-1) = 3. Is this correct? Yes again. One last equation. 5(34) + 6(-27) + 3(-1) = 5. That's correct as well. The answer is A.
In case you still weren't sure if the answer was A or not;
B: 2(33) + 2(-26) + 6(0) = 14. Right away we can see that B will be incorrect.
C: 2(35) + 2(-28) + 6(-2) = 2. Again, incorrect.
D: 2(36) + 2(-29) + 6(1) = 20. Incorrect!
A is the correct answer.
Find the median, mean, and range.
14, 1, 16, 6, 15, 2
Answers
Answer:
Median: 10
Mean: 9
Range: 15
Step-by-step explanation:
Have a good day :)
Find the volume of the given solid over the indicated region of integration. f(x,y) = 2x +2y ? 5; R = {(x,y): - 4 leq x leq 1, 3 leq y leq 6} What is the volume of the region? Units^3
Answers
The volume of the given solid over the indicated region of integration, f(x,y) = 2x + 2y - 5 and R = {(x,y): -4 ≤ x ≤ 1, 3 ≤ y ≤ 6}, is 63 units³.
To find the volume, we will integrate the function f(x,y) over the region R. Follow these steps:
1. Set up the double integral: ∬R (2x + 2y - 5) dA
2. Set up the limits of integration: ∫(from -4 to 1) ∫(from 3 to 6) (2x + 2y - 5) dy dx
3. Integrate with respect to y: ∫(from -4 to 1) [(2xy + 2y²/2 - 5y)] (evaluated from 3 to 6) dx
4. Simplify and evaluate: ∫(from -4 to 1) [6x + 18 - 5(6-3)] dx
5. Integrate with respect to x: [3x² + 18x - 15x] (evaluated from -4 to 1)
6. Simplify and evaluate: (3 + 18 - 15) - (-12 + 72 + 60)
7. Calculate the final result: 6 - (-30) = 36
The volume of the region is 63 units³.
To know more about double integral click on below link:
https://brainly.com/question/2289273#
#SPJ11
consider the function f(x)=2x3 21x2−48x 6,−8≤x≤2. find the absolute minimum value of this function. answer:
Answers
The absolute minimum value of the function
\(f(x)=2x3 21x2−48x 6\)
,\(−8≤x≤2\) is -414 at
x = 6.
To find the absolute minimum value of the function
\(f(x) = 2x^3 - 21x^2 - 48x + 6\) in the interval
-8 ≤ x ≤ 2, follow these steps:
1. Determine the derivative of f(x) with respect to x to find critical points:
\(f'(x) = 6x^2 - 42x - 48\)
2. Set f'(x) to 0 and solve for x to find critical points:
x = 6, -2
3. Check the function's value at the critical points and the endpoints of the interval:
\(f(-8) = 2560, f(-2) = 72, f(6) = -414, f(2) = -52\)
4. Compare the values and determine the absolute minimum value, Therefore,The absolute minimum value of the function is -414 at x = 6.
To know more about absolute minimum, refer to the link :
https://brainly.com/question/29030328#
#SPJ11
A landscaper is designing a display of flowers for an area in a public park. The flower seeds will be planted at points that lie on a circle that has a diameter of 8 feet. the point where any seed is planted must be 2 feet away from the seeds on either side of it. what is the maximum number of flower seeds that can be planted using the design?
after planting the flower seeds the landscaper has 20 seeds left over. the landscaper wants to plant all of the remaining seeds in another circle so that the seeds are 2 feet apart. what is the diameter of the smallest circle that the landscaper can use to plant all of the remaining seeds?
Answers
The z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
The z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
How to find the Z score
P(Z ≤ z) = 0.60
We can use a standard normal distribution table or a calculator to find that the z-score corresponding to a cumulative probability of 0.60 is approximately 0.25.
Therefore, the z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
For the second question:
We want to find the z-score such that the area under the standard normal distribution curve to the right of z is 0.30. In other words:
P(Z ≥ z) = 0.30
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to a cumulative probability of 0.30 is approximately -0.52 (since we want the area to the right of z, we take the negative of the z-score).
Therefore, the z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
Read more on Z score here: brainly.com/question/25638875
#SPJ1
10. Set up and evaluate the definite integral for the area of the surface generated by revolving the curve a) (3 pts.)y= 6x 3+ 2x1 ,1≤x≤2, about the x-axis; b) (3 pts.) x= 4y−1,1≤y≤4, about the y-axis.
Answers
The definite integral for the area of the surface generated by revolving the curve y = 6x^3 + 2x about the x-axis, over the interval 1 ≤ x ≤ 2, can be set up and evaluated as follows:
∫[1 to 2] 2πy √(1 + (dy/dx)^2) dx
To calculate dy/dx, we differentiate the given equation:
dy/dx = 18x^2 + 2
Substituting this back into the integral, we have:
∫[1 to 2] 2π(6x^3 + 2x) √(1 + (18x^2 + 2)^2) dx
Evaluating this definite integral will provide the surface area generated by revolving the curve about the x-axis.
b) The definite integral for the area of the surface generated by revolving the curve x = 4y - 1 about the y-axis, over the interval 1 ≤ y ≤ 4, can be set up and evaluated as follows:
∫[1 to 4] 2πx √(1 + (dx/dy)^2) dy
To calculate dx/dy, we differentiate the given equation:
dx/dy = 4
Substituting this back into the integral, we have:
∫[1 to 4] 2π(4y - 1) √(1 + 4^2) dy
Evaluating this definite integral will provide the surface area generated by revolving the curve about the y-axis.
By setting up and evaluating the definite integrals for the given curves, we can find the surface areas generated by revolving them about the respective axes. The integration process involves finding the appropriate differentials and applying the fundamental principles of calculus.
To know more about integral follow the link:
https://brainly.com/question/33191486
#SPJ11
a sample survey is to be conducted to determine the mean family income in an area. the question is how many families should be sampled? in order to get more information about the area, a small pilot survey was conducted, and the standard deviation of the sample was computed to be $400 with the mean of $60,000. the sponsor of the survey wants you to use the 0.99 degree of confidence. the estimate is to be within $90. how many families should be interviewed?
Answers
The sample size required is 182 families should be interviewed.
To calculate the number of families that should be interviewed to obtain the desired precision and degree of confidence, one must first determine the minimum sample size required to achieve the desired degree of confidence. As the standard deviation of the sample was computed to be $400 with the mean of $60,000.
Sample size formula: n = (Z² * s²) / E²
The formula for the degree of confidence: Z = 2.576
Sample size formula: n = (Z² * s²) / E²
Substituting the values, we get n = (2.576² * $400²) / $90²= 181.49 = 182 families. The sample size required is 182 should be interviewed families.
To learn more about "Standard deviation": brainly.com/question/23907081
#SPJ11
please help I will give brainalist

Answers
Answer:
6.2
Step-by-step explanation:
Answer:
x=2+3√2 or x=2−3√2
Step-by-step explanation:
if you buy two tickets to the fair that costs $30 . what is the unit rate per 1 ticket
Answers
Answer:
15/per 1 ticket
Which is SMALLER, -6.3 or -6.1?
Answers
my explanation is because -6.3 is less than -6.1 so technically it makes it smaller. if you were to add to -6.3 you would get -6.1 on the x axis.
an open-top box is to be constructed from a square piece of cardboard, 3 feet wide, by cutting out a square from each corner and bending up the sides. what is the largest volume that the box can have?
Answers
The largest volume that the box can have is 02.
equation for volume :
v = x (3- 2x)²
Differentiating using chain rule and product line:
v' = 1(3 - 2x)² + 2x (3 -2x) (-2)
= 9 - 12x + 4x² -12x +8x²
= 9 - 24x +12x²
Finding the critical value where v' = 0
v' = 0
⇒12x² - 24x +9 =0
⇒3 ( 4x² -8x +3)=0
⇒ 4x² -8x+3 =0
(2x- 3) (2x-1) =0
or, x=3/2 or 1/2
putting the value x= 1/2, we get,
V = 2
Learn more about volume :
https://brainly.com/question/22907480
#SPJ4
The heights of the low tides for four days are 20.22 ft, 2.64 ft, 20.22 ft, and 2.64 ft. What is the mean height of the low tides?
Answers
Answer:
11.43 ft
Step-by-step explanation:
Mean = sum of low tides / total number of low tides
(20.22 ft + 2.64 ft + 20.22 ft + 2.64 ft.) / 4 = 11.43ft
in a survey conducted on an srs of 200 american adults, 72% of them said they believed in aliens. give a 95% confidence interval for percent of american adults who believe in aliens.
Answers
A 95% confidence interval for percent of american adults who believe in aliens: (0.6578, 0.7822)
In this question we have been given that in a survey conducted on an srs of 200 american adults, 72% of them said they believed in aliens
We need to find the 95% confidence interval for percent of american adults who believe in aliens.
95% confidence interval = (p ± z√[p(1 - p)/n])
Here, n = 200
p = 72%
p = 0.72
And the z-score for 95% confidence interval is 1.960
The upper limit of interval would be,
(p + z√[p(1 - p)/n])
= 0.72 + 1.960 √[0.72(1 - 0.72)/200]
= 0.72 + 1.960 √[(0.72 * 0.28)/200]
= 0.72 + 1.960 √0.001008
= 0.72 + 0.0622
= 0.7822
The lower limit of interval would be,
(p - z√[p(1 - p)/n])
= 0.72 - 1.960 √[0.72(1 - 0.72)/200]
= 0.72 - 1.960 √[(0.72 * 0.28)/200]
= 0.72 - 1.960 √0.001008
= 0.72 - 0.0622
= 0.6578
Therefore, a 95% confidence interval = (0.6578, 0.7822)
Learn more about 95% confidence interval here:
https://brainly.com/question/15683202
#SPJ4
Today, the members of the cabinet Group of answer choices are an informal group of presidential advisers. are limited to the heads of the fifteen executive departments. include fourteen department secretaries and the attorney general, plus other top officials chosen by the president. include only the heads of the Departments of State, Justice, Defense, and Treasury, plus the heads of the EPA, CIA, and FBI. are a subset of any six executive department heads, chosen by the president.
Answers
Answer:
include fourteen department secretaries and the attorney general, plus other top officials chosen by the president.
Step-by-step explanation:
The Cabinet of the United States of America is a government body which includes the vice president along with the heads executive branch. The President of the United States in the executive head of the body.
It mainly consists of the secretaries of 14 departments as well as the attorney general and other officials who are chosen by the President of the US.
What is the y-intercept of y = 3 – 4x?
Answers
Answer:
3
Step-by-step explanation:
y=mx+b
b is the y-intercept
OR
Because the y-intercept is (0,y) plug 0 for x
y=3-4(0)
y=3