Joy has a ribbon that measures 16 yards. She cuts 9 pieces of ribbon to decorate gifts. Each piece of ribbon that Joy cuts measures 4 feet.
What is the length, in yards, of the remaining ribbon?
Answers
Answer:
4 yds
Step-by-step explanation:
So... 16 yards is 48 feet (because one yard is 3 feet so I just multiplied by 3)
and she cuts 9 pcs of ribbon each 4 feet
so it's 9 x 4 = 36
48 - 36 = 12
And 12 feet equals 4 yards
So, Joy has 4 yards of remaining ribbon
Answer:
9.3 yards
Step-by-step explanation: the exact answer is 9.3333333
Related Questions
it takes three identical water pumps 7 hours to fill a pool, how long would it take two of the same pumps to fill the pool, assuming they all pump at the same rate. please help
Answers
Answer:
10.5 hrStep-by-step explanation:
7 hr/3 pumps
So first we want to find the unit rate which would be...
5.25 hr/1 pump
Now that we found the unit rate we are going to multiply it by 2 because there are 2 pumps...
5.25*2=10.5
So our answer is 10.5 hr/ 2 pumps
YOUR WELCOME!
BRAINLIEST?????
3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11
Evaluate the following:
9 + (-2)
-25 + 11
-12 -15
25 ÷ -5
33 × 2
15 × - 10
-220 ÷ -5
-6 + -7
Answers
1. 9 + (-2) = 7
2. -25 + 11 = -14
3. -12 -15 = -27
4. 25 ÷ -5 = -5
5. 33 × 2 = 66
6. 15 × - 10 = -150
7. -220 ÷ -5 = 44
8. -6 + -7 = -13
Five number have amean of 12,when one number is removed, the mean becomes 11,what is the removed number
Answers
Answer:
The removed number is 16
Step-by-step explanation:
Five numbers have a mean of 12.
Now;
Mean = Σx/x
Thus; Σx = 12 × 5 = 60
Now,we are told that if one number is removed, the mean is 11.
Thus;
(60 - x)/4 = 11
60 - x = (11 × 4)
60 - x = 44
x = 60 - 44
x = 16
Thus,the removed number is 16
The function y = −16x² + 32x + 25 represents the height y (in feet) of a pinecone x seconds after falling from a tree.
a. After how many seconds does the pinecone hit the ground?
b. A second pinecone falls from a height of 36 feet. Which pinecone hits the ground in the least amount of time? Explain.
Answers
a. The pinecone hits the ground approximately 3.97 seconds after falling from the tree.
b. The pinecone falling from a height of 36 feet hits the ground in the least amount of time, approximately 0.72 seconds.
How to calculate the valuea For our equation, a = -16, b = 32, and c = 25. Plugging these values into the quadratic formula, we get:
x = (-32 ± √(32² - 4(-16)(25))) / (2(-16))
x = (-32 ± √(1024 + 1600)) / (-32)
x = (-32 ± √2624) / (-32)
x = (-32 + √2624) / (-32) ≈ 3.97 seconds
b. Using the quadratic formula again:
x = (-b ± √(b² - 4ac)) / (2a)
In this case, a = -16, b = 32, and c = -11. Substituting these values into the quadratic formula, we have:
x = (-32 ± √(32² - 4(-16)(-11))) / (2(-16))
x = (-32 ± √(1024 - 704)) / (-32)
x = (-32 ± √320) / (-32)
x = (-32 + √320) / (-32) ≈ 0.72 seconds
The pinecone falling from a height of 36 feet hits the ground in the least amount of time, approximately 0.72 seconds.
Learn.more about functions on
https://brainly.com/question/10439235
#SPJ1
how do i write the inequality of this?

Answers
Answer:
\(y \geqslant \frac{2}{3} x - 2\)
\(y + 2 \geqslant \frac{2}{3} x\)
\( \frac{2}{3}x - y \leqslant 2\)
\(2x - 3y \leqslant 6\)
pls help :P i know it's easy

Answers
Answer:
(-4,-8)
Step-by-step explanation:
Two bicyclists ride in opposite directions. The speed of the first bicyclist is 5mph faster than the second. After 2 hours they are 70 miles apart. Find their rates.
Answers
Answer:
A. 15 mi/h; 20 mi/hr
Step-by-step explanation:
Increase 2800kg
by 21
Answers
Answer:
3388 kg
Step-by-step explanation:
If you mean to increase by 21%, then
You may
100% + 21% = 121%
2800 x 121/100
2800 x 1.21
= 3388 kg
IF YOU ANSWER THIS RIGHT NOW ILL GIVE YOU 64 POINTS
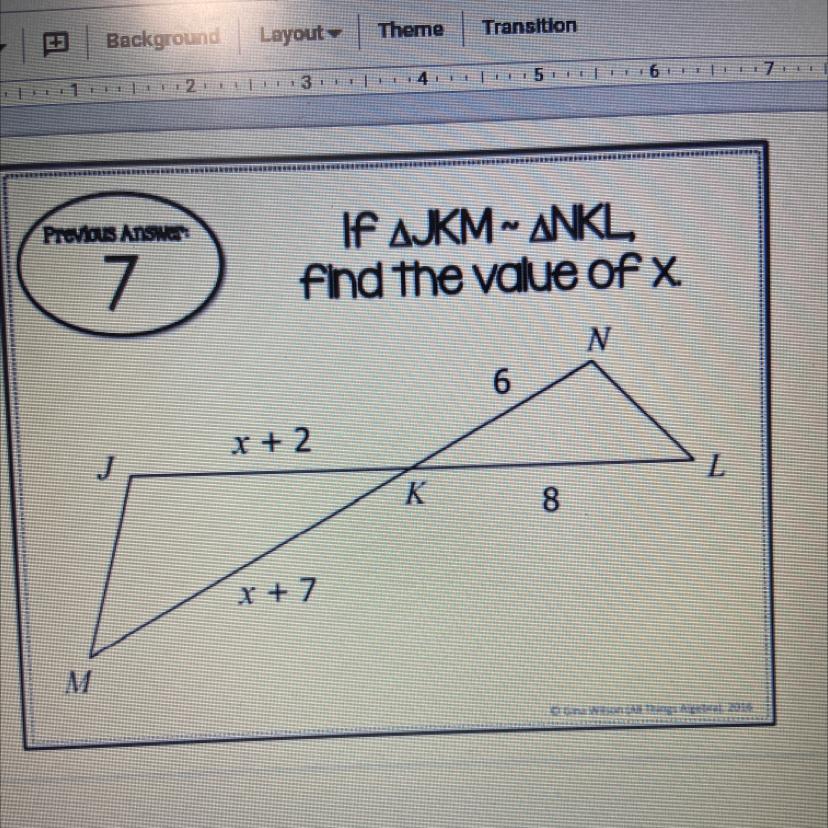
Answers
Answer:
13 = x
Step-by-step explanation:
\(\frac{6}{8}\) = \(\frac{(x + 2)}{(x + 7)}\)
6x + 42 = 8x + 16
42 = 2x + 16
\(\frac{26}{2}\) = \(\frac{2x}{2}\)
13 = x
Use mental math to find the sum.
150 + 20 + 25
Answers
Answer:
50 + 20 = 70
70 + 25 = 95
150 + 95 = 245
In conclusion, 150 + 20 + 25 equals to a total amount of 215.
Step-by-step explanation:
Have a great rest of your day
#TheWizzer
hemo
150 + 20 + 25
= 100 +50+20+20+5
= 100+90+5
=195
PLEASEE HELP!!!!NO LINKS
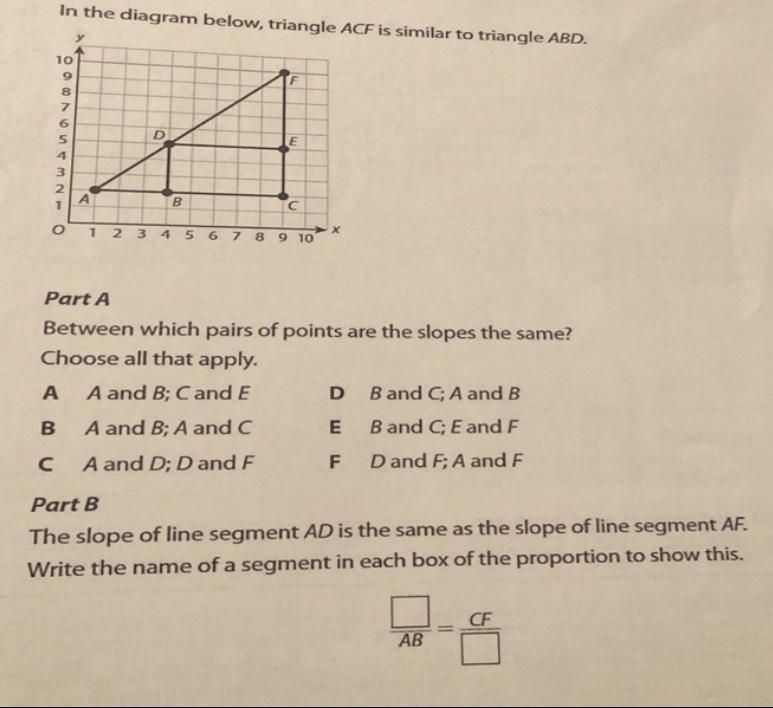
Answers
Answer:
I think it's choice B and D
Step-by-step explanation:
they both are a straight line and would both have a slope of zero. between point A and D is a slope obviously but D and F would not be the same slope because the line gets steeper. that's how I look at it. I'm pretty sure that's it.
The lengths of a professor's classes has a continuous uniform distribution between 50.0 min and 52.0 min. If one such class is randomly selected, find the probability that the class length is between 50.2 and 50.7 min.
Answers
The probability can be found using the formula for a continuous uniform distribution: P(50.2 ≤ X ≤ 50.7) = (50.7 - 50.2) / (52.0 - 50.0).
P(50.2 ≤ X ≤ 50.7) = 0.5
Therefore, the probability that the class length is between 50.2 and 50.7 min is 0.5. This means that the likelihood of selecting a class length within this range is 50%, which is relatively high given the range of possible lengths.
The lengths of the professor's classes follow a continuous uniform distribution between 50.0 minutes and 52.0 minutes. To find the probability that the class length is between 50.2 and 50.7 minutes, we can use the following formula for a continuous uniform distribution:
P(a ≤ X ≤ b) = (b - a) / (B - A)
Here, A = 50.0 min (lower bound), B = 52.0 min (upper bound), a = 50.2 min, and b = 50.7 min.
Plugging in the values:
P(50.2 ≤ X ≤ 50.7) = (50.7 - 50.2) / (52.0 - 50.0)
P(50.2 ≤ X ≤ 50.7) = 0.5 / 2
P(50.2 ≤ X ≤ 50.7) = 0.25, So, the probability that the class length is between 50.2 and 50.7 minutes is 0.25 or 25%.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
Can someone please help me ?

Answers
Answer:
14 is +1
15 is -9
Step-by-step explanation:
In a recent survey, 8 people were each asked the number of times they have been on an airplane. Here is a list of the responses.
9, 20,18 , 22,11 ,22 ,15 , 4
Find the range of the data set.
Answers
Answer:
18
Step-by-step explanation:
the range is how far from the smallest number to the biggest number in the set so 22-4 is 18
Work Shown:
Range = max - min = 22 - 4 = 18
The range represents the distance from the smallest item to the largest item. It tells us how spread out the data set is, in a sense.
Please help 5 questions I need help





Answers
Answer:
1. <2, <7
2. 58
3. 78
4. a and b
h5. <2 and <7 ( i think this is the same question as the first one)
Step-by-step explanation:
2. 2x + 7 = 123 (you have to make them equal to each other because they are consecutive interior angles)
2x + 7 = 123, subtract 7
2x = 116, divide 2 for both sides to make x by itself
x = 58
3. 78 because of consecutive interior angles
Is 2x-4=2x-7 infinite no solution or one solution
Answers
Answer:
no solution
Step-by-step explanation:
1) Use the distributive property to factor the expression.
-24x+64
Answers
Answer:
-8(3x-8)
Step-by-step explanation:
Factor -8 out of -24x+64
Please help me find the answer to this problem.

Answers
Answer:
numerator - is 2, 15, 18, 6
denominator - is 12, 14, 33, 8, 64
Step-by-step explanation:
2/10, 4/12, 8/14, 9/33, 1/8, 12/64, 15/55, 18/66, 6/32
find the probability of selecting a black checker from a bag of 6 black and 4 red checkers, replacing it and selecting another black
Answers
The probability of selecting a black checker from a bag of 6 black and 4 red checkers, replacing it, and selecting another black is 9/25.
To find the probability follow these-
Determine the probability of selecting a black checker on the first draw.
There are 6 black checkers and a total of 10 checkers (6 black + 4 red).
So, the probability of selecting a black checker on the first draw is 6/10,
which can be simplified to 3/5.
Since the black checker is replaced, there are still 6 black checkers and
a total of 10 checkers in the bag. Therefore, the probability of selecting a
black checker on the second draw is also 3/5.
To find the probability of both events occurring, multiply the probabilities together: (3/5) × (3/5) = 9/25.
So, the probability of selecting a black checker from a bag of 6 black and
4 red checkers, replacing it, and selecting another black is 9/25.
for such more question on probability
https://brainly.com/question/27342429
#SPJ11
Identify the interval(s) on which the quadratic function is positive.
y = 5x² - 46x + 77
Answers
Answer:
Step-by-step explanation:
y = 5x² - 46x + 77
If you want the roots they are 11/5 and 7 both positive.
Which of the following is not true of a normal curve?a. It is skewed.b. It is a probability distribution.c. Its total area contains 100% of the cases.d. The mode, median, and mean are identical.
Answers
The statement that is not true of a normal curve is a. It is skewed.
A normal curve, also known as a bell curve or Gaussian distribution, is a symmetric probability distribution.
This means that it is not skewed, and it has a shape that is roughly like a bell. The curve is defined by its mean and standard deviation, which determine its center and spread. The total area under the curve represents 100% of the cases or observations in the distribution. The area under the curve between any two points represents the proportion of cases falling between those points. The mode, median, and mean are identical in a normal curve, which means that they all represent the center of the distribution. The mode is the most frequently occurring value, the median is the middle value, and the mean is the arithmetic average of all the values.In summary, a normal curve is a symmetric probability distribution that is not skewed, and its total area contains 100% of the cases.
Know more about the Gaussian distribution
https://brainly.com/question/27774617
#SPJ11
Need help with these 3 problems!

Answers
Answer:
1. 25
2. 44
3. 9
Step-by-step explanation:
Answer:
25 students44 cents9 eggsStep-by-step explanation:
If there are 3 cookies for each student and 75 cookies in total, then the equation would be 75 ÷ 3. that equals 2588 total for 2 cans. Divide 88 by 2 for the unit price. That makes 44 cents. 45 eggs total, 5 layers. Divide 45 by 5. That makes 9 eggs per layer.When ringing up a customer, a cashier needs 30 seconds to process payment as well as 3 seconds to scan each item being purchased. How long does it take to ring up a customer with 24 items? Write and solve an equation to find the answer.
Answers
3x + 16 = 136
(3 seconds per item, plus 16 seconds to process payment, equals 136 seconds total.)
Subtract 16 from each side. Then divide both sides by 3.
a check or quadrangle is defined by the intersection of pairs of
Answers
A check or quadrangle is defined by the intersection of pairs of diagonals of a parallelogram.
What is a parallelogram?A parallelogram is a quadrilateral with two pairs of parallel sides. In a parallelogram, the opposite sides are parallel and have the same length. The opposite angles of a parallelogram are equal. A parallelogram is a unique type of quadrilateral with specific characteristics.
What is a check or quadrangle?A quadrangle or check is defined as the intersection of pairs of diagonals of a parallelogram. In other words, it is the area inside the parallelogram that is divided into four triangles, each of which shares a common vertex in the center of the parallelogram.
The diagonals of a parallelogram are the line segments that connect the opposite vertices of a parallelogram. When these diagonals intersect, they form four triangles, which are also known as the parallelogram's "sub-triangles." The point where the diagonals intersect is called the center of the parallelogram, and it divides each diagonal into two equal parts.
To know more about parallelogram refer here:
https://brainly.com/question/1563728#
#SPJ11
a runner is running a 10k race. the runner completes 30% of the race in 20 minutes. if the runner continues at the same pace, what will her final time be?
Answers
we first need to figure out how long the entire 10k race will take the runner.
Since the runner has completed 30% of the race in 20 minutes, we can use that information to estimate the total time it will take the runner to complete the entire race.
To do this, we can use a proportion. If the runner completed 30% of the race in 20 minutes, we can set up the equation: 30/100 = 20/x, Here, x represents the total time it will take the runner to complete the race. To solve for x, we can cross-multiply:
30x = 100 * 20
30x = 2000
x = 2000/30
x ≈ 66.67
So, the runner will complete the entire 10k race in approximately 66.67 minutes. Next, we need to determine whether the runner can maintain the same pace for the entire race. If the runner can maintain the same pace, we can use the information we have to estimate the runner's final time.
If the runner completed 30% of the race in 20 minutes, we can use that to calculate how long it will take the runner to complete the remaining 70% of the race. To do this, we can set up the equation: 30/100 = 20/x, Solving for x, we get: x = 20 * 100 / 30, x ≈ 66.67/3, x ≈ 22.22 .
So, the runner will complete the remaining 70% of the race in approximately 22.22 minutes if she can maintain the same pace. Adding this time to the 20 minutes the runner has already completed, we get: 20 + 22.22 = 42.22,
Therefore, if the runner can maintain the same pace, her final time for the 10k race will be approximately 42.22 minutes.
To know more about equation click here
brainly.com/question/649785
#SPJ11
What is the following product? RootIndex 5 StartRoot 4 x squared EndRoot times RootIndex 5 StartRoot 4 x squared EndRoot.
Answers
You can use the fact that whenever bases are same, the product of such quantities end up getting their exponents added.
The product result of given expression is \(^5\sqrt{(2x)^4}\)
When does the power add in multiplication?Suppose you've got two values to multiply with each other and you have got both value's bases same, then the multiplication will end up with result being that base raised with sum of the exponents of both the initial values.
For example:
\(a^b \times ^c =a^{b+c}\)
How to find the product result for given expression?You can convert the roots to powers. Then you can use the fact that the bases are same and thus the powers will add.
Remember that if you've got xth root, then the power would be 1/x.
For our case, it will go like this:
\(^5\sqrt{4x^2} \times ^5\sqrt{4x^2} = \: ^5\sqrt{(2x)^2} \times ^5\sqrt{(2x)^2} = {((2x)^2)}^{\frac{1}{5}} \times {((2x)^2)}^{\frac{1}{5}} = (2x)^{\frac{2}{5}} \times (2x)^{\frac{2}{5}}\\\\ ^5\sqrt{4x^2} \times ^5\sqrt{4x^2} = (2x)^{\frac{2}{5} + \frac{2}{5}} = (2x)^{\frac{4}{5}} = \: ^5\sqrt{(2x)^4}\)
Thus, the final product result will be written as \(^5\sqrt{(2x)^4}\)
Learn more about base and exponent here:
https://brainly.com/question/9047706
What are the 3 types of rigid transformations?
Answers
Three types of rigid transformations are Reflection, Rotation, and Translation. Rigid transformation, also called isometry.
A rigid transformation, also called isometry, is a transformation that doesn't change the size or shape of a geometric figure. The following are 3 types of rigid transformation:
1. Reflection
→ is the act of shifting an object's coordinates that flip it across a line without changing its shape or size. Horizontal (draw a figure to the left or right) or vertical (draw a figure to the up or down) reflections are possible. The result of reflection is a mirror image of the figure itself.
The figure is reflected across \(x-\) or \(y-\) axis, and then change \(x-\) or \(y-\) coordinate.
2. Rotation
→ is the non-modification of an object's size or shape by rotating it around an fixed point. A center of rotation is required to rotate an object. And the rotation did by using a degree.
The figure is rotated by a degree (ex: 90°), and then change \(x-\) or \(y-\) coordinate. Meanwhile, a point's center rotation stays at the same.
3. Translation
→ is sliding a figure in any direction without changing its size, shape, or orientation. Translation could be horizontal (make a figure left or right), or vertical reflections (make a figure up or down).
Vertical translation is shifting the graph along \(y-\) axis
Horizontal translation is shifting the graph along \(x-\) axis.
Here to learn more about Rigid Transformation:
https://brainly.com/question/1462871
#SPJ4
The middle 50% of the distribution for X, the bounds of which form the distance represented by the IQR, lies between what two values
Answers
The middle 50% of the distribution for X, the bounds of which form the distance represented by the IQR, lies between the first and third quartiles of the data set.
Specifically, the first quartile (Q1) marks the 25th percentile of the data set, while the third quartile (Q3) marks the 75th percentile.
The difference between Q3 and Q1 is known as the interquartile range (IQR).The IQR is a helpful measure of spread in a data set since it excludes outliers from the calculation. Outliers are any data points that fall outside of 1.5 times the IQR above the third quartile or below the first quartile of the data set. Therefore, the middle 50% of the distribution for X lies between Q1 and Q3, with the IQR representing the range of values between these two quartiles.
Know more about distance represented by the IQR here:
https://brainly.com/question/10577037
#SPJ11
in a study of a disease in which all cases that developed were ascertained, if the relative risk for the association between a factor and the disease is equal to or less than 1.0, then:
Answers
For the given statement , correct answer is option e: there is either no association or a negative association between the factor and the disease.
Reason with explanation:
Relative risk is a ratio which help us to compares the risk of a health between two groups. When the value of relative risk is 1, it represents the risk among the two groups is same. When the value of relative risk is > 1, it represents the risk is increased for the exposed group. And when relative risk < 1, it represents exposure protect against the disease. Hence for the given statement , a value of relative risk is equal or less than represents there is no association or negative association between a factor or a disease.The complete question is:
In a study of a disease in which all cases that developed were ascertained, if the relative risk for the association between a factor and the disease is equal to or less than 1.0, then:
a. There is no association between the factor and the disease
b. The factor protects against development of the disease
c. Either matching or randomization has been unsuccessful
d. The comparison group used was unsuitable, and a valid comparison is not possible
e. There is either no association or a negative association between the factor and the disease
Learn more about factors here
brainly.com/question/14516061
#SPJ4