LAST QUESTION ON TEST, DESPERATELY NEED HELP
Solve the following: -4x - 2 = -2(1 - 4x)
Answers
Answer:
x = 0
Step-by-step explanation:
Related Questions
What will the movement of a point which is on the surface of a circle touching the ground at the same time, if the circle turns 210 degree by moving forward? The radius of he circle is 50cm.
Answers
Answer:
183.26cm
Step-by-step explanation:
Radius of the Circle = 50cm
Let the point be at A
It turns forward 210 degrees to B.
Therefore, the central angle subtended by the arc AB = 210 degrees
The movement of the point from A to B will be the length of the arc AB.
\(\text{Length of an arc }=\dfrac{\theta}{360} \times 2\pi r \\$Therefore, the distance moved forward$\\=\dfrac{210}{360} \times 2\times\pi \times 50\\\\=183.26$ cm\)
Plzz help Drag each graph to the correct location on the table.
The points on the graphs represent relations. Classify these relations according to whether or not they are functions.

Answers
Answer:
Functions: Second Graph
The other two are not. Use the vertical line test. I'm pretty sure but not 100%
Step-by-step explanation:
The volume of a box is 192 cubic inches.
The height is 4 inches. The width is 2
inches more than the length. Find the
missing dimensions.
Answers
Answer:
base=24
Step-by-step explanation:
2*4=8
192/8=24
what are those equations simplified

Answers
2. 13d^3g^6
3. c^2m^4p^6
4.5k^6m^2
identify an equation in point-slope for the line parellel to y= 1/2 x-7 that passes through (-3 , -2)
Answers
Answer:
y+2=1/2(x+3)
Why?
Point slope form is written as (y-y1) = m(x-x1) with y1 being the value of y at a certain point, x1 being the value of x at a certain point, and m being slope. y1 and x1 are given to us by the point (-3, -2) letting us know that y1=-2 and x1=-3. The only thing left to find is slope. Parallel lines have the same slope. If the line we are trying to find is parallel to the one given in the question, we just need to find the slope of the equation given. That equation is given in slope-intercept form which is y = mx + b. m is still slope so we can see that the slope is 1/2. Now we can plug m, x1 and y1 into the point slope form equation to get y + 2 = 1/2(x + 3)
Let P(t) be the population (in millions) of a certain city t years after 2015 , and suppose that P(t) satisfies the differential equation P ′(t)=0.06P(t),P(0)=3. (a) Use the differential equation to determine how fast the population is growing when it reaches 5 million people. (b) Use the differential equation to determine the population size when it is growing at a rate of 700,000 people per year. (c) Find a formula for P(t).
Answers
(a) To determine how fast the population is growing when it reaches 5 million people, we can substitute P(t) = 5 into the differential equation P'(t) = 0.06P(t). This gives us P'(t) = 0.06(5) = 0.3 million people per year. Therefore, the population is growing at a rate of 0.3 million people per year when it reaches 5 million people.
(b) To determine the population size when it is growing at a rate of 700,000 people per year, we can set P'(t) = 700,000 and solve for P(t). From the given differential equation, we have 0.06P(t) = 700,000, which implies P(t) = 700,000/0.06 = 11,666,666.67 million people. Therefore, the population size is approximately 11.67 million people when it is growing at a rate of 700,000 people per year.
(c) To find a formula for P(t), we can solve the differential equation P'(t) = 0.06P(t). This is a separable differential equation, and integrating both sides gives us ln(P(t)) = 0.06t + C, where C is the constant of integration. By exponentiating both sides, we get P(t) = e^(0.06t+C). Using the initial condition P(0) = 3, we can find the value of C. Substituting t = 0 and P(0) = 3 into the equation, we have 3 = e^C. Therefore, the formula for P(t) is P(t) = 3e^(0.06t).
Learn more about integration here: brainly.com/question/32386391
#SPJ11
Find the variable of x.
8x-2=-9+7x
Answers
Answer:
8x-2=-9+7x equals X=-7
Answer:
x = -7
Step-by-step explanation:
The area of a parallelogram is 40 square units. One side of the parallelogram is 64 units long. The other side is 8 units long. Determined wheather each dimension could be the height of the parallelgram.
Answers
Answer:
The side with 64 units cannot be the height of the parallelogram and the side with 8 units can be the side of the parallelogram.
Step-by-step explanation:
Area of parallelogram= 40 sq units
One side of the parallelogram= 64 units
∴ the dimension with 64 units cannot be the height of the parallelogram because the side is more than area. When multiplying with the other side, the area will be more than 40.
Other side of the parallelogram= 8
∴ the dimension with 8 units is possible and it can be the height of the parallelogram because the side is less than area. When multiplying with the other side, the area will be 40.
Help me with math!!!

Answers
Answer:
- 7
Step-by-step explanation:
Given
t < - 6
Then t = - 7 is less than - 6 and is a solution
sketch the curve with the given polar equation. θ = −π/6
Answers
To sketch the curve with polar equation θ = −π/6, we need to plot all the points (r, θ) that satisfy the equation for various values of r. Since θ is fixed at −π/6, all the points will lie on a line at an angle of −π/6 to the positive x-axis.
The value of r can be positive or negative, so we will plot points both above and below the x-axis.
Since r can be any value, we will just choose a few values for illustration purposes. Let's choose r = 1, 2, −1, and −2. Then the corresponding points are:
(1, −π/6), (2, −π/6), (−1, −π/6), and (−2, −π/6)
We can plot these points on a polar coordinate system as follows:
These points lie on a line at an angle of −π/6 to the positive x-axis, as expected. Note that the sign of r determines whether the point lies above or below the x-axis.
To know more about polar coordinate refer here:
https://brainly.com/question/11657509
#SPJ11
A poster of area 8640 cm2 has blank margins of 10 cm wide on the top and bottom and 6 cm wide on the sides. Find the dimensions that maximize the printed area. (Use decimal notation. Give your answers as whole or exact numbers.)
Answers
Therefore, the dimensions that maximize the printed area are 4 cm × 2156 cm.
Let's first find the dimensions of the printable region of the poster.
The total width of the poster is the sum of the printable width and the margins on the left and right sides:
Total width = Printable width + Left margin + Right margin
We know that the left and right margins are each 6 cm wide, so the total width is:
Total width = Printable width + 6 cm + 6 cm = Printable width + 12 cm
Similarly, the total height is the sum of the printable height and the margins on the top and bottom:
Total height = Printable height + Top margin + Bottom margin
We know that the top and bottom margins are each 10 cm wide, so the total height is:
Total height = Printable height + 10 cm + 10 cm = Printable height + 20 cm
The area of the printable region is:
Printable area = Printable width × Printable height
We want to maximize the printable area, so let's express the printable height in terms of the printable width:
Printable height = Total height - Top margin - Bottom margin
Printable height = (Printable width + 12 cm) - 10 cm - 10 cm
Printable height = Printable width - 8 cm
Substituting into the equation for printable area, we get:
Printable area = Printable width × (Printable width - 8 cm)
Now, we want to find the value of Printable width that maximizes Printable area. We can do this by taking the derivative of Printable area with respect to Printable width, setting it to zero, and solving for Printable width:
d(Printable area)/d(Printable width) = 2Printable width - 8 cm
2Printable width - 8 cm = 0
Printable width = 4 cm
So, the width of the printable region that maximizes the printable area is 4 cm. Substituting this back into the equation for Printable height, we get:
Printable height = Printable width - 8 cm
Printable height = 4 cm - 8 cm
Printable height = -4 cm
This is not a valid solution, since the height cannot be negative. Therefore, we made an error somewhere.
Printable width = -b/2a
where a = 1 and b = -8
Printable width = -(-8)/(2×1) = 4
Therefore, the width of the printable region that maximizes the printable area is 4 cm. Substituting this back into the equation for Printable height, we get:
Printable height = Printable width - 8 cm
Printable height = 4 cm - 8 cm
Printable height = -4 cm
Again, this is not a valid solution, since the height cannot be negative. However, we can see that the maximum occurs when Printable width is 4 cm, so the maximum printable area is:
Printable area = Printable width × Printable height
Printable area = 4 cm × (8640 cm / 4 cm - 16 cm)
Printable area = 4 cm × 2156 cm
Printable area = 8624 cm
Learn more about dimensions visit: brainly.com/question/27404871
#SPJ4
Help would be more than appreciated:)

Answers
\(40 \times 0.80 = 32\)
\(32 \times 12 = 384\)
He gains £384
\(40 - 32 = 8\)
\(8 \div 2 = 4\)
\(2(12) + 2(6) = 36\)
He gains £36
//
\( - 130 + 384 + 36 = 290\)
Ryan made £290
//
I'm not too sure about this...
Anyway if he sold 80% of the jumpers at a normal price, he would earn £384.
There are 8 left and he managed to sell half of those but there is a promo where you can buy one at full price and get one for half the price so only two of the four can be bought at full price while the other two gets bought at half price. He earns £36 from this.
If you take in account the starting cost and add the profits, he made a total of £290 selling jumpers.
But again, I'm not too sure.
The system shown is blank.
a.) inconsistent
b.) equivalent
c.) consistent

Answers
Answer:
I think it's consistent
Step-by-step explanation:
Use a number line to order the numbers from least to greatest.
HELLLPPPP!!!!!

Answers
Beth performed an experiment in which she randomly drew one napkin at a time from a drawer, with replacement. The drawer contained one napkin each of gray, cyan, beige, lilac, and crimson colors. The results of her experiment are shown below.
Napkin Color Times Drawn
gray 7
cyan 20
beige 11
lilac 3
crimson 22
Based on the experiment above, predict the number of times a cyan napkin would be drawn if she performs the experiment a total of 189 times.
A.
60
B.
59
C.
61
D.
58
Answers
The expected number of times that a cyan napkin would be drawn if she performs the experiment a total of 189 times is given as follows:
A. 60.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
The total number of trials is given as follows:
7 + 20 + 11 + 3 + 22 = 63.
Hence the probability of drawing a cyan napkin is given as follows:
p = 20/63.
Meaning that the expected number of times that a cyan napkin would be drawn if she performs the experiment a total of 189 times is obtained as follows:
E(X) = 189 x 20/63
E(X) = 60.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
Your starting salary at a new company is $34,000 and it increase by 2.5%
each year. What will your salary be in 5 years? Round your answer to the
nearest dollar.
$ 85000
$ 38468
$ 41303
$ 46700
$ 37102
Answers
Answer:
2.5x100÷340000=
5x340000/1000
a bakery used 25% more butter this month than last month if the bakery used 240 kilograms of butter last month how much did it use this month
Answers
Answer:
300
Step-by-step explanation:
25% of 240 is 60.
( 13 + 25.8 - 6.05 + 12.8 - 32.65 ) x
( 12.05 - 30.4 + 21.65 ) = ?
Answers
Answer: 42.57
Step-by-step explanation:
To solve this equation, you will first need to add the numbers inside the first parenthesis.
12.9 (12.05 - 30.4 + 21.65)
Then, you will need to add the numbers inside the second parenthesis.
12.9 x 3.3
Multiply the two numbers together, and then you will get 42.57. Therefore, that will be the answer to your equation!
For more information on long - step operation problems, go to:
https://brainly.com/question/22012761
How can I describe a ordered pair
Answers
Answer:
Ordered Pair An ordered pair is a composition of the x coordinate (abscissa) and the y coordinate (ordinate), having two values written in a fixed order within parentheses. It helps to locate a point on the Cartesian plane for better visual comprehension. The numeric values in an ordered pair can be integers or fractions.
Step-by-step explanation:
i hope this helped! :)
Answer:
An ordered pair contains the coordinates of one point in the coordinate system. A point is named by its ordered pair of the form of (x, y). The first number corresponds to the x-coordinate and the second to the y-coordinate. To graph a point, you draw a dot at the coordinates that corresponds to the ordered pair.
Step-by-step explanation:
If a voter votes RIGHT in one election, the probability that the voter will vote LEFT in the next election is 0.2. If a voter votes LEFT in one election, the probability that the voter will vote RIGHT in the next election is 0.1. Assume that these are the only two parties available to vote for. 1. What is the Markov assumption? 2. Draw the transition diagram to this problem. 3. Write down the transition matrix. 4. If 55% of the electorate votes RIGHT one year, find the percentage of voters who vote RIGHT the next year. What would be the voter percentages in 10 years' time? Interpret your result. (2+2+3 marks) 5. Will there ever be a steady state where the party percentages don't waiver? Interpret your result. (3+3 marks)
Answers
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
The Markov assumption in this context is that the probability of a voter's next vote depends only on their current vote and not on their past voting history. In other words, the Markov assumption states that the future behavior of a voter is independent of their past behavior, given their current state.
Transition diagram:
LEFT RIGHT
|--------->--------|
LEFT | 0.8 0.2 |
| |
RIGHT| 0.1 0.9 |
|--------->--------|
The diagram represents the two possible states: LEFT and RIGHT. The arrows indicate the transition probabilities between the states. For example, if a voter is currently in the LEFT state, there is a 0.8 probability of transitioning to the LEFT state again and a 0.2 probability of transitioning to the RIGHT state.
Transition matrix:
| LEFT | RIGHT |
---------------------------
LEFT | 0.8 | 0.2 |
---------------------------
RIGHT | 0.1 | 0.9 |
---------------------------
The transition matrix represents the transition probabilities between the states. Each element of the matrix represents the probability of transitioning from the row state to the column state.
If 55% of the electorate votes RIGHT one year, we can use the transition matrix to find the percentage of voters who vote RIGHT the next year.
Let's assume an initial distribution of [0.45, 0.55] for LEFT and RIGHT respectively (based on 55% voting RIGHT and 45% voting LEFT).
To find the percentage of voters who vote RIGHT the next year, we multiply the initial distribution by the transition matrix:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1] = [0.62, 0.38]
Therefore, the percentage of voters who vote RIGHT the next year would be approximately 38%.
To find the voter percentages in 10 years' time, we can repeatedly multiply the transition matrix by itself:
[0.45, 0.55] * [0.2, 0.9; 0.8, 0.1]^10 ≈ [0.503, 0.497]
After 10 years, the voter percentages would be approximately 50.3% for LEFT and 49.7% for RIGHT.
Interpretation: The results suggest that over time, the voter percentages will tend to approach an equilibrium point where the percentages stabilize. In this case, the percentages stabilize around 50% for both LEFT and RIGHT parties.
No, there will not be a steady state where the party percentages don't waiver. This is because the transition probabilities in the transition matrix are not symmetric. The probabilities of transitioning between the parties are different depending on the current state. This indicates that there is an inherent bias or preference in the voting behavior that prevents a steady state from being reached.
Learn more about probability at:
brainly.com/question/13604758
#SPJ4


Hi , please help and explain fully ! ( I don't understand how to work this one out)

Answers
Answer:
to 1dp = -2.6
to 2 dp= -2.64
as fraction = 29/-11
Step-by-step explanation:
x+1 = 6(2x+5) - you multiply each side by 2x + 5
x+1 =12x+30 - expanding the brackets
x-12x+1=30 - subtract 12x from both sides
x -12x = 30-1 - subtract one from both sides
-11x = 29 - you just work each side out to get these answers
29/-11 =x - divide -11 from both sides
-2.63636363636 =x - using a calculator ( if finding whole number ) you do 29/-11
to 1dp = -2.6
to 2 dp= -2.64
Look at the picture and thanks

Answers
Answer:
51 notes
Step-by-step explanation:
Firstly we need to get the value of the 200 pounds in koruna
From the question, 1 pound is 25.82
200 pounds will be;
200 * 25.82
= 5,164 koruna
So to know the number of possible 100 koruna bills, we simply need to divide what we have by 100
We have this as :
5,164/100
= 51.64
So the number of notes she would be is 51 100 koruna notes
A university interested in tracking its honors program believes that the proportion of graduates with a GPA of 3.00 or below is less than 0.09. In a sample of 260 graduates, 20 students have a GPA of 3.00 or below. The value of the test statistic and its associated p-value are __________.
Answers
The test static value is 1.44 and its associated p-value is 0.1335.
Given that the problem deals with the concept of test for single proportion. The parameter of the interest is the population proportion of graduates with GPA of 3.00 or below is less than 0.09.
Let the population proportion be p=0.09.
Let the number of graduates in a sample be n=260.
Let the number of students have a GPA of 3.00 or below be x=20.
Based on the known data, the null and alternative hypothesis are,
H₀:p≥0.09
H₁:p<0.09
The sample proportion of students have a GPA of 3.00 or below is,
\(\begin{aligned}\hat{p}&=\frac{x}{n}\\ &=\frac{20}{260}\\ &=0.07\end\)
Under the null hypothesis, the test static value is,
\(\begin{aligned}z&=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\\ &=\frac{0.07-0.09}{\sqrt{\frac{0.09(1-0.09)}{260}}}\\ &=\frac{-0.02}{0.018}\\ &=-1.11\end\)
The p-value for the left-tailed test is
p-value=p(z<-1.11)
p-value=0.1335
Hence, the value of the test statistic and its associated p-value for the proportion of graduates with a GPA of 3.00 or below is less than 0.09. are 1.44 and 0.1335.
Learn more about null hypothesis from here brainly.com/question/9954556
#SPJ4
Please help! Simplify the expression 2^4x3^y/8*3^x
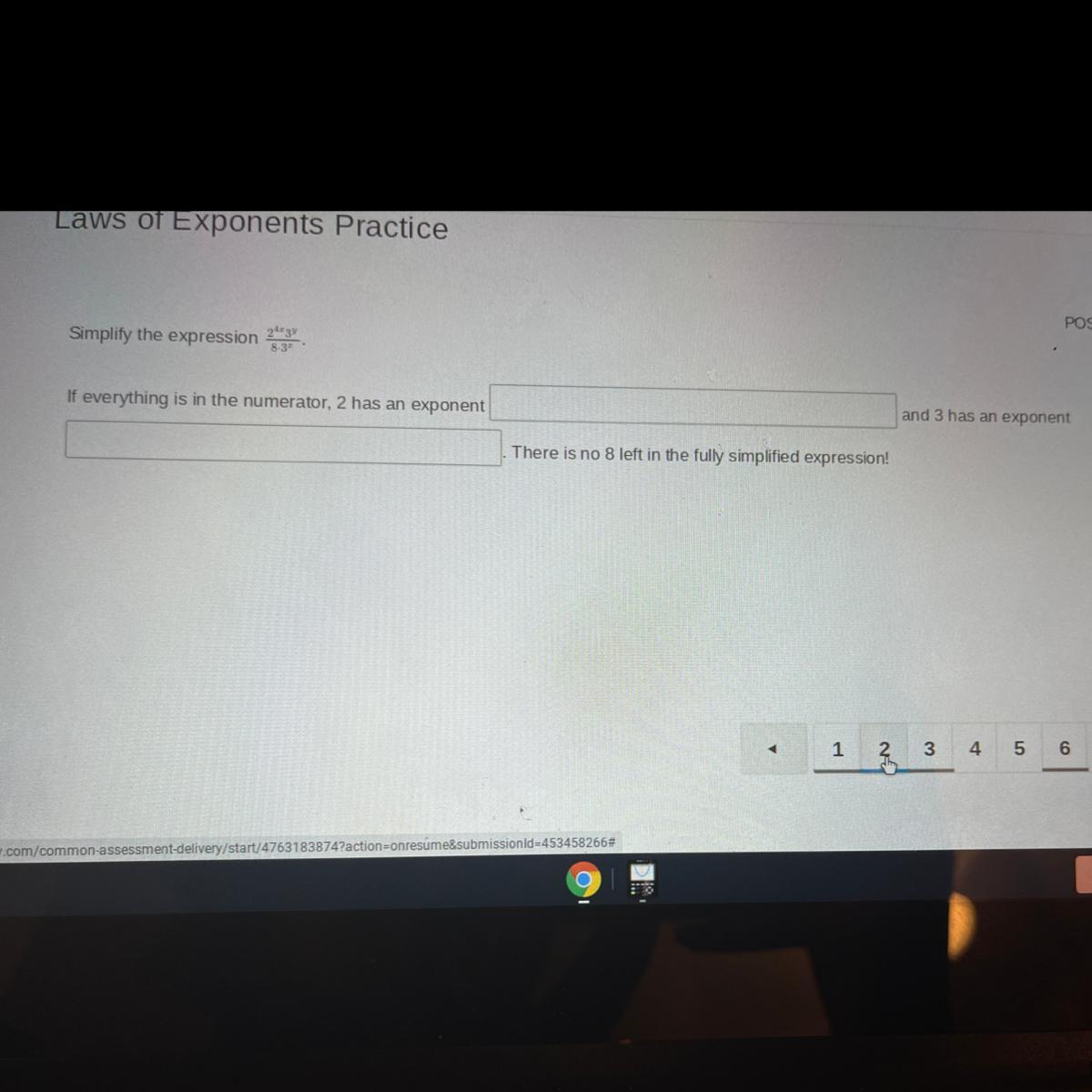
Answers
Answer
the answer is (3×16^x×y)/(8-3^x )
Step-by-step explanation:
I need help with traingle and using pyhagorean therom to find missing side lenght.
Answers
The missing side of the triangle, B, is approximately 13.86 units long.
Let's denote the missing side as B. According to the Pythagorean Theorem, the sum of the squares of the lengths of the two shorter sides of a right triangle is equal to the square of the length of the longest side, which is the hypotenuse. Mathematically, this can be represented as:
A² + B² = C²
In our case, we are given the lengths of sides A and C, which are 8 and 16 respectively. Substituting these values into the equation, we get:
8² + B² = 16²
Simplifying this equation gives:
64 + B² = 256
To isolate B², we subtract 64 from both sides of the equation:
B² = 256 - 64
B² = 192
Now, to find the value of B, we take the square root of both sides of the equation:
√(B²) = √192
B = √192
B ≈ 13.86 (rounded to two decimal places)
To know more about Pythagorean theorem here
https://brainly.com/question/343682
#SPJ4
Complete Question:
How do you use the Pythagorean Theorem to find the missing side of the right triangle with the given measures: A= 8, C= 16?
Write two expressions for the perimeter of the figure.
2
8
4x
4
7x
Note: The figure is not drawn to scale.
(a) Use all five side lengths.
perimeter = 0+0+0+0+0
(b) Simplify the expression from part (a).
perimeter =
Answers
The perimeter can be calculated using the formulas 22x+23 and 2x+3x+17x+7+16.
How to calculate perimeter of two expression ?The length of a shape's outline is its perimeter. You must add the lengths of all four sides of a rectangle or square to determine its perimeter. In this instance, x represents the rectangle's length and y its width. The surface of a shape's area is measured.
The total length of the four sides makes up the perimeter (P) of a rectangle. A rectangle has two equal lengths and two equal widths since its opposite sides are equal. The following is the formula for calculating a rectangle's perimeter: The formula for perimeter is length + length + width + width. P = l + l + w + w.
you want to add the variables of the same kind in this case
2x
3x 7
17x 16
_________
22x + 23
Therefore Two expressions for the perimeter would be 22x+23 and 2x+3x+17x+7+16
The complete question is : Write two expressions for the perimeter of the figure.
2x
7
3x
172
16
Note: The figure is not drawn to scale.
(a) Use all five side lengths.
perimeter - ] + + + +
(b) Simplify the expression from part (a).
perimeter =
Х
$ ?
To learn more about perimeter refer to :
https://brainly.com/question/19819849
#SPJ1

The cost of a cell phone plan varies directly with the amount of data included. A 0.5 GB plan costs $14.95 per month. How much does a 3 GB plan cost?
Answers
Answer:
Step-by-step explanation: D. (24, 12), (36, 0)
Consider the function g(x)=−(x−1)^3−2. Which ordered pair lies on the inverse of the function?
(62,−3)
(−4, 123)
(3, 1)
(3,−6)
Answers
The ordered pair lie on the inverse of the function is (62,−3).
Option A is the correct answer.
What is a function?A function is a relationship between inputs where each input is related to exactly one output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
f(x) = -(x - 1)³ - 2
The inverse of f(x).
y = -(x - 1)³ - 2
interchange x and y and solve for y.
x = -(y - 1)3 - 2
(y - 1)³ = -2 - x
(y - 1)³ = -(2 + x)
Cuberoot on both sides.
y - 1 = ∛-(2 + x)
y = ∛-(2 + x) + 1
Now,
Substitute in the inverse of g(x).
(62, -3) = (x, y)
(−4, 123) = (x, y)
(3, 1) = (x, y)
(3,−6) = (x, y)
So,
y = ∛-(2 + x) + 1
y = ∛-(2 + 62) + 1
∛-1 = -1
y = -1∛64 + 1
y = -1 x 4 + 1
y = -4 + 1
y = -3
So,
(62, -3) ______(1)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 - 4) + 1
∛-1 = -1
y = ∛(-2 + 4) + 1
y = ∛2 + 1
y = 1.26 + 1
y = 2.26
So,
(-4, 2.26) _______(2)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) _______(3)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) ______(4)
Thus,
From (1), (2), (3), (4) we see that,
(62, -3) is the solution to the inverse of g(x).
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
Equation A (x+yi)+(4-7i) = 3-4i
Equation B (x+yi)-(-6+14i) = 18+2i
In equation A, x = and y =
in equation B, x = and y =
Answers
In equation A, the values of x =-1 and y = 3
In equation B, the values of x = 12 and y = 16.
Given that :
Equation A :
(x+ yi)+(4-7i) = 3-4i
Simplify it.
x + 4 = 3
⇒ x = 3 - 4 = -1
Also :
y - 7 = -4
⇒ y = 3
Equation B :
(x+yi)-(-6+14i) = 18+2i
x - -6 = 18
⇒ x = 18 - 6 = 12
y - 14 = 2
y = 2 + 14 = 16
Learn more about Equations here :
https://brainly.com/question/29538993
#SPJ4
A cylinder and a cone have congruent bases and heights what will be the relationship of the volumes of the two figures
the volike of the cylinder will be twice the volume of the cone
Answers
The ratio of the volume of the figure is 3:1.
The term called volume in math is defined as the space occupied within the boundaries of any three-dimensional solid
Here we know that the cylinder and a cone are having equal radii of their bases and heights.
Then let us consider that radius of the cone is equal to radius of the cylinder is defined as r and Height of the cone and height of the cylinder is defined as h.
Then their volume is written as,
=> Volume of cylinder /volume of cone
=> πr²h/ (1/3)πr²h
When we simplified this on, then we get the fraction as,
=> 3/1
Then the resulting ratio is 3:1.
To know more about Volume here.
https://brainly.com/question/11168779
#SPJ4