Last week's and this week's low temperatures are shown in the table below.
Low Temperatures for 5 Days This Week and Last Week
Low Temperatures
This Week (°F)
4
10
6
9
6
Low Temperatures
Last Week (°F)
13
9
5
8 5
Which measures of center or variability are greater than 5 degrees? Select three choices.
the mean of this week's temperatures
the mean of last week's temperatures
the range of this week's temperatures
the mean absolute deviation of this week's temperatures
the mean absolute deviation of last week's temperatures
Next
Mark this and return
Save and Exit
Submit
Answers
Answer:
A, B, C
Step-by-step explanation:
bc, I think...
Related Questions
Calculate the angle of elevation from the
base of this leaning tower, B, to the point P.
Give your answer to 1 d.p.

Answers
Answer:
\(43.78^\circ\)
Step-by-step explanation:
Let θ be the angle that the base of the leaning tower makes with the tower i.e. the angle of elevation
Since this is a right triangle we have the relationship
\(\tan\theta = \dfrac{height}{base} = \dfrac{46}{48} \approx 0.95833\\\\\)
\(\theta = tan^{-1} (0.95833) = 43.78^\circ\)
Answer
\(= 43.78^\circ\)
The angle of elevation is given by the trigonometric relation and θ = 73.40°
What are trigonometric relations?
Trigonometry is the study of the relationships between the angles and the lengths of the sides of triangles
The six trigonometric functions are sin , cos , tan , cosec , sec and cot
Let the angle be θ , such that
sin θ = opposite / hypotenuse
cos θ = adjacent / hypotenuse
tan θ = opposite / adjacent
tan θ = sin θ / cos θ
cosec θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ
Given data ,
Let the angle of elevation be represented as E = θ
Now , the measure of the altitude = 46 m
The measure of the hypotenuse = 48 m
And , the angle of elevation is given by the trigonometric relation ,
sin θ = opposite / hypotenuse
On simplifying , we get
sin θ = 46 / 48
sin θ = 0.958333
Taking inverse on both sides , we get
θ = sin ⁻¹ ( 0.958333 )
θ = 73.40°
Hence , the angle of elevation is 73.40°
To learn more about trigonometric relations click :
https://brainly.com/question/14746686
#SPJ2
A manufacturing company regularly conducts quality control checks at specified periods on the products it manufactures. Historically, the failure rate for LED light bulbs that the company manufactures is 3%. Suppose a random sample of 10 LED light bulbs is selected. What is the probability that:
a. None of the LED light bulbs are defective?
b. Exactly one of the LED light bulbs is defective?
c. Two or fewer of the LED light bulbs are defective?
d. What are the mean and standard deviation of the binomial distribution for the number of defective LED light bulbs?
Answers
Answer:
a) There is a 59.87% probability that none of the LED light bulbs are defective.
b) There is a 31.51% probability that exactly one of the light bulbs is defective.
c) There is a 98.84% probability that two or fewer of the LED light bulbs are defective.
d) There is a 100% probability that three or more of the LED light bulbs are not defective.Step-by-step
explanation:
For each light bulb, there are only two possible outcomes. Either it fails, or it does not. This means that we use the binomial probability distribution to solve this problem.
Find the exact value of each of the remaining trigonometric functions of θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
Answers
The exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
Given that sec(θ) = -8 and sin(θ) > 0, we can find the exact values of the remaining trigonometric functions using the Pythagorean identity:
sec^2(θ) = 1/sin^2(θ)
Substituting the value of sec(θ), we have:
(-8)^2 = 1/sin^2(θ)
64 = 1/sin^2(θ)
sin^2(θ) = 1/64
sin(θ) = ±√(1/64)
Since sin(θ) > 0, we take the positive square root:
sin(θ) = √(1/64)
Next, we use the reciprocal identity for cosecant:
csc(θ) = 1/sin(θ)
Substituting the value of sin(θ), we have:
csc(θ) = 1/√(1/64) = 8√(1/64) = 8/√(64) = 8/8 = 1
Next, we use the reciprocal identity for cotangent:
cot(θ) = 1/tan(θ)
We can find the value of tan(θ) using the definition:
tan(θ) = sin(θ) / cos(θ)
Substituting the values of sin(θ) and cos(θ), we have:
tan(θ) = √(1/64) / (-8) = -√(1/64) / 8
Finally, we use the reciprocal identity for a tangent:
tan(θ) = 1/cot(θ)
Substituting the value of cot(θ), we have:
tan(θ) = -8√(1/64)
Therefore, the exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
The complete question is:-
Find the exact value of each of the remaining trigonometric functions of
θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
To learn more about trigonometric functions, refer:-
https://brainly.com/question/6904750
#SPJ4
Let A be an event within the sample space S, and let n(A) a and n(S) s. Use the complements principle of counting to find an expression for n(A)
Answers
The expression for n(A) using the complements principle of counting is n(A) = n(S) - n(A').
How to find expression for n(A) using the complements principle of counting is n(A) = n(S) - n(A').The complements principle of counting states that the number of outcomes in the complement of event A is equal to the total number of outcomes in the sample space S minus the number of outcomes in event A.
Using this principle, we can express the number of outcomes in event A, n(A), as:
n(A) = n(S) - n(A')
Where:
- n(A) represents the number of outcomes in event A.
- n(S) represents the total number of outcomes in the sample space S.
- n(A') represents the number of outcomes in the complement of event A.
Therefore, the expression for n(A) using the complements principle of counting is n(A) = n(S) - n(A').
Learn more about complements principle at https://brainly.com/question/10810074
#SPJ1
The weights X of an animal are distributed according to the
probability distribution shown.
What is the probability that the animal's weight will be less than
151 pounds?
O 0.25
O 0.50
O 0.60
O 0.75
Answers
The probability that the animal's weight will be less than 151 pounds is 0.50.
The correct option is B.
What is the probability that the animal's weight will be less than 151 pounds?Since the given probability distribution ranges from 148 to 152, and we need to find the probability that the animal's weight will be less than 151 pounds, we can add the probabilities corresponding to the weights less than 151.
From the distribution, we see that the probability of the animal's weight being less than 151 pounds is 0.2 + 0.3 = 0.5.
Therefore, the answer is O 0.50.
Learn more about probability at: https://brainly.com/question/251701
#SPJ1
a random sample of 50 students at a large high school resulted in a 95 percent confidence interval for the mean number of hours of sleep per day of (6.73, 7.67). which of the following statements best summarizes the meaning of this confidence interval?
Answers
There is a 95% chance that the true mean number of hours of sleep per day for all students in the school falls within this range
To calculate the 95% confidence interval for the mean number of hours of sleep per day of a random sample of 50 students from a large high school, you would need to follow these steps:
Calculate the mean of the sample by adding up all the hours of sleep reported and dividing by the sample size (n).
Calculate the standard deviation (σ) of the sample by taking the square root of the sum of squares of the differences between the sample values and the mean divided by n1.
Calculate the standard error (SE) by dividing the standard deviation by the square root of n.
Calculate the margin of error (ME) by multiplying the standard error by the critical value of 1. 96.
Calculate the confidence interval by adding and subtracting the margin of error from the mean. This will give you the lower and upper bounds of the confidence interval.
Therefore, the 95% confidence interval for the mean number of hours of sleep per day of a random sample of 50 students from a large high school is (6. 73, 7. 67). This means that there is a 95% chance that the true mean number of hours of sleep per day for all students in the school falls within this range
Learn more about confidence interval:
https://brainly.com/question/17212516
#SPJ4
PLZ HELP ILL MARK BRAINLIEST!!!
A football player lost 20 yards on the first play. On the second play, he gained 12 yards. How many yards ahead or behind is he from where he started? (Hint: draw yourself a number line to visualize this problem)
Answers
The football player is 8 yards behind
If you wanted to do a number line you could start from 0 - 20 and count down 12 yards. the remaining pegs you have left are what it is. so 8 yards.
How do I put this in slope- intercept form
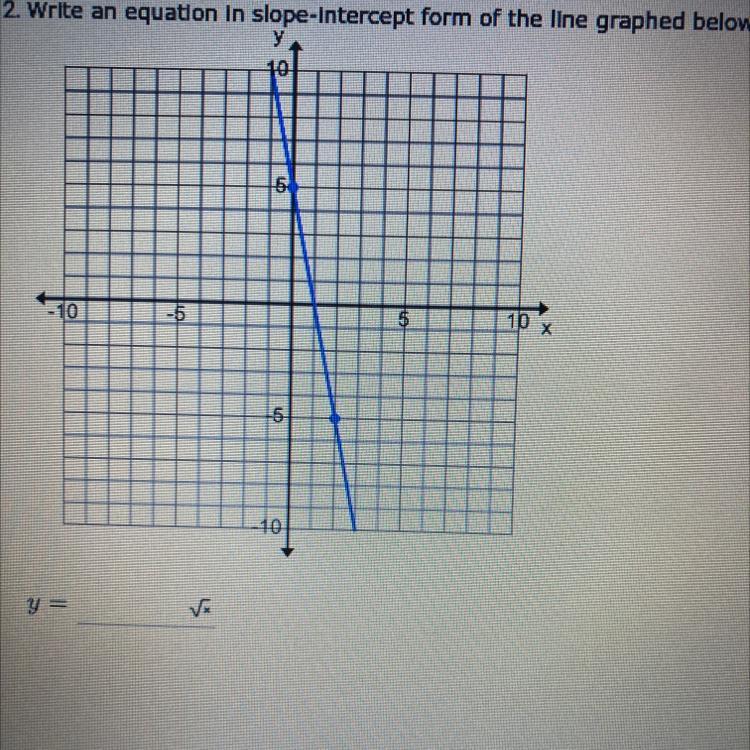
Answers
Answer:
y=-5x+5
Step-by-step explanation:
Olivia does chores every Saturday morning. She spends 1/3 of her time cleaning her room. Of the remaining 2/3 of her time, she spends 6/7 of it cleaning the kitchen. How much of Olivia's total time does she spend cleaning the kitchen?]
Answers
Answer:
she spends 9 hours
Step-by-step explanation:
Sketch the graph of the function below, including correct signs, x-intercepts and y-
intercepts.
f(x) = (x + 2)²(x – 5)2
y
200
180
160
140
120
100
80
60
40
20
-10 9 8 7 6 5 4 3 2
1
2
3
5
6
7
9
10
-1
-20
-40
-60
-80
-100
- 120
-140
-160
-180
-200
Answers
Answer:
Sketch the graph of the function below, including correct signs, x-intercepts and y-
intercepts.
f(x) = (x + 2)²(x – 5)2
y
200
180
160
140
120
100
80
60
40
20
-10 9 8 7 6 5 4 3 2
1
2
3
5
6
7
On a map, the scale shown is 1 inch : 5 miles. If
a wildlife refuge is 50 square miles, what is the
area of the refuge on the map?
Use the proportion to solve for x.
1 in. 2
25 mi2
x in. ²
50 mi²
Cross
multiplication
can help!
=
The area of the wildlife refuge is [?] square
inches on the map.
Enter

Answers
Answer:
Step-by-step explanation:
6
look at pic to see what I need

Answers
Answer:
60-9+15=66 is the answer.
F f(x) = 6x – 4, what is f(x) when x = 8?
Answers
Answer:
F(x) = 44
Step-by-step explanation:
f(x) = 6x - 4
x = 8
f(x) = 6(8) - 4
f(x) = 48 - 4
Answer:
Step-by-step explanation:
f(8) = 6(8) - 4= 48 - 4 = 44
What is the slope of y = 1/5x - 3
Answers
Answer:
ITS 15 THANK ME LATER!!!!
Step-by-step explanation:
Answer:
M = 1/5
Step-by-step explanation:
84102 - 1052=?
pasagot po pls with solution
Answers
Answer:
83050
Step-by-step explanation:
that's the answer to the question
producto de (10x+7)(10x-7)
Answers
Answer:
(10x−7)^2
Step-by-step explanation:
(10x+7)(10x-7)
i stead of making it a "100" since they are both the same but positive and negative () and bring it to the power of 2
Can you help me in this question?

Answers
Answer:
the answer is third option B
Please help me out :c I am also marking brainliest, can you show how you got the answer also? ty if u do

Answers
Answer:
Store a $90.30
Store B is $87.75
store B is the cheapest
Step-by-step explanation:
Just subtract 129.0 by 35% and 135.0 by 35%
Store a $90.30
Store B is $87.75
store B is the cheapest
Step-by-step explanation:
Just subtract 129.0 by 35% and 135.0 by 35%
The quotient of twenty and a number, decreased by 4, is equal to zero
Answers
The equation associated with the quotient of twenty and a number, decreased by 4, is equal to zero is 20/x - 4 = 0 and that number will be 5.
How to form an equation?Determine the known quantities and designate the unknown quantity as a variable while trying to set up or construct a linear equation to fit a real-world application.
In other words, an equation is a set of variables that are constrained through a situation or case.
Let's say that number is x,
Quotients of 20 and x will be given as 20/x
20/x - 4 = 0
20/x = 4
x = 20/4 = 5
Hence"The equation associated with the quotient of twenty and a number, decreased by 4, is equal to zero is 20/x - 4 = 0 and that number will be 5".
For more about the equation,
https://brainly.com/question/10413253
#SPJ1
Can anyone help me with this question please

Answers
Answer:
1 = 130° , 2 =50° , 3 = 85°, 4=45°
Step-by-step explanation:
1 =45 + 85 = 130 { sum of opposite interior angle equals exterior angle}
2 = 180 - 1 { angles on a straight line equals 180}
= 180 -130 = 50°
4 = 180 - 135 = 45° { angles on a straight line equals 180}
3 = 135 -2 { sum of opposite interior angles equals exterior angle; 3 + 2 = 135}
3 = 135-50 = 85°
Note : sum of opposite interior angles equals external exterior angle, let's prove it:
If we look at the triangle at the bottom left, we have :
85, 45 and r { let's denote r as the missing angle}
So 85 + 45 + r = 180° { sum of angles of a triangle}
By simple arithmetic
r = 180 - ( 85+45) = 180 - 130 = 50°
but r + 4 = 180° { sum of angles in a straight line equals 180°}
4 = 180 - 50 = 130°
So you see 4 is the exterior angle of the triangle opposite to 85° and 45° interior angles}
What is the total amount of outcomes possible when a coin is tossed four times and a card if selected from a standard deck of cards.
Answers
Answer:
About 60 pecent
Step-by-step explanation:
Answer: 832 possible outcomes
To find the total number of outcomes when a coin is tossed four times and a card is selected from a standard deck of cards, we need to multiply the number of outcomes for each event.
The number of outcomes for a coin toss is 2 (heads or tails), and we toss the coin 4 times. Therefore, the number of outcomes for the coin tosses is:
2 x 2 x 2 x 2 = 16
The number of outcomes when selecting a card from a standard deck of cards is 52. Therefore, the total number of outcomes when a coin is tossed four times and a card is selected from a standard deck of cards is:
16 x 52 = 832
So there are 832 possible outcomes when a coin is tossed four times and a card is selected from a standard deck of cards.
which are undefined? sec(-pi/2) csc(3pi) cot(7pi/2) csc(-3pi/2) cot(5pi/3)
Answers
Answer:
\(csc(3\pi ), sec(\frac{-\pi}{2})\)
The Undefined term is csc(3pi) and sec(-pi/2) .
What is Trigonometry?The area of mathematics that deals with particular angles' functions and how to use those functions in calculations. There are six popular trigonometric functions for an angle. Sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant are their respective names and acronyms (csc).
Given:
As, Cosecant is the reciprocal of sine, so the cosecant of any angle x for which sin x = 0 must be undefined, since it would have a denominator equal to 0. The value of sin (pi) is 0, so the cosecant of pi must be undefined.
Thus, csc(3pi) is undefined
and, the value of The value of cos (pi/2) is 0, so the secant of (pi)/2 must be undefined.
Thus, sec(-pi/2) is also undefined.
Learn more about Trigonometry here:
https://brainly.com/question/29002217
#SPJ2
Jefferson's Popcorn & Roasted Nuts Shop sells cone-shaped bags of roasted cashews, shown below. What is the volume of the bag of nuts?

Answers
The volume of the bag of nuts is the amount of nuts it can contain
The volume of the bag of nuts is 84.78 cubic inches
How to determine the volume of the bag?From the figure, we have the following parameters:
Radius, r = 3 inHeight, h = 9 inThe volume of a cone is calculated using:
V = 1/3 πr^2h
Substitute the known values
V = 1/3 * 3.14 * 3^2 * 9
Evaluate the product
V = 84.78
Hence, the volume of the bag of nuts is 84.78 cubic inches
Read more about volumes at:
https://brainly.com/question/1972490
a collecting jar holds 45 insects. 4/5 of the insects are purple
Answers
36 of the insects are purple
4 x 45 . = 35
5 . 1
5 goes into 45 9 times so 4 x 9 =36
I need help please I can only find 2 of these solutions

Answers
Step 1: Isolate the Sin Operator
\(8 sin(\frac{\pi }{6} x)=2\\sin(\frac{\pi }{6} x)=0.25\\\\\)
Step 2: Use Inverse Sin(arcsin) to isolate the term with the x variable
Note that since trig functions have 2 general solutions, this will give us one of our general solutions.
\(x=\frac{6 arcsin(0.25)}{\pi } =0.48\)
x₁= 0.48
Solving for x₂
Use the period identity for Sin Functions
\(sin(x)=sin(\pi -x)\)
X in this case is arcsin(0.25)
\(\frac{\pi }{6} x=\pi -arcsin(0.25) = 5.52\)
So our two general solutions are 0.48 and 5.52
Step 3: Period
Trig Functions have periodic behavior and this function period is
\(\frac{2\pi }{1} (\frac{6}{\pi } )= 12\)
So our general solutions are
0.48±12k, where k is an integer
5.52±12k, where k is an integer
Let k=1, and we get our next set of solutions:
12.48 and 17.52
So our answer is 0.48,5.52,12.48,17.52
This graph represents a quadratic function. What is the function's equation written in factored form and in vertex form?
(graph in picture)

Answers
Step-by-step explanation:
f(x) = a(x-x1) (x-x2)
from the vertex, we get a:
0 = a(4-2)²- 8
4a = 8
a = 2
so, the equation:
f(x) = 2(x-0) (x-4)
f(x) = 2x(x-4)
f(x) = 2x² -8x
Suppose the man in the St. Ives poem has x wives, each wife has x sacks, each sack has x cats, and each cat has x kits. Write an expression using exponents that represent the total number of kits, cats, sacks, and wives.
Please I got to at least get a 90 on my homework
Answers
The total number of kits, cats, sacks and wives is x⁴+x³+x²+x
What is an exponential expression?Exponential expressions are just a way to write powers in short form. The exponent indicates the number of times the base is used as a factor. For example 3×3×3×3 can be written as 3⁴.
A man has x wives, each wife has x sack, therefore the number of sack = x×x = x²
each sack has x cats, therefore the number of cats = x²×x = x³
each cats has x kits, therefore the number of kits = x³× x= x⁴
therefore the total number of kits , cats, sacks and wives = kits + cats+ sacks + wives= x⁴+x³+x²+x.
learn more about exponential expression from
https://brainly.com/question/2456547
#SPJ1
Need help with this question

Answers
Answer:
Yes, it is a solution because inserting 8 into the equation gives you 13.
Step-by-step explanation:
1/2(8) + 9 = 13
4 + 9 = 13
13 = 13
please help me asap

Answers
Answer: Number 1: = and Number 2: is C
Step-by-step explanation:
Answer:
6. >
7. 5/6, 2/3, 8/15
Step-by-step explanation:
For 6, you need to make the denominators equal, so you need to multiply 6/3*5 making it 30/15. Now which is greater 30/15 or 10/15 and you can see it's 30/15 so it would be >. For 7 you need to do the same thing but make all three denominators the same. 2/3 becomes 20/30 by multiplying by 10. 5/6 becomes 25/30 by multiplying by 5. Lastly, 8/15 becomes 16/30 by multiplying by 2. Now all their denominators are the same, so now all you have to do is order them. 25/30, 20/30, and 16/30. This is equal to 5/6, 2/3, 8/15.
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.
