Let me know if the image isn’t clear enough. Solved it already just can’t understand the table given that try’s to explain how to round the answer.
Answers
So,
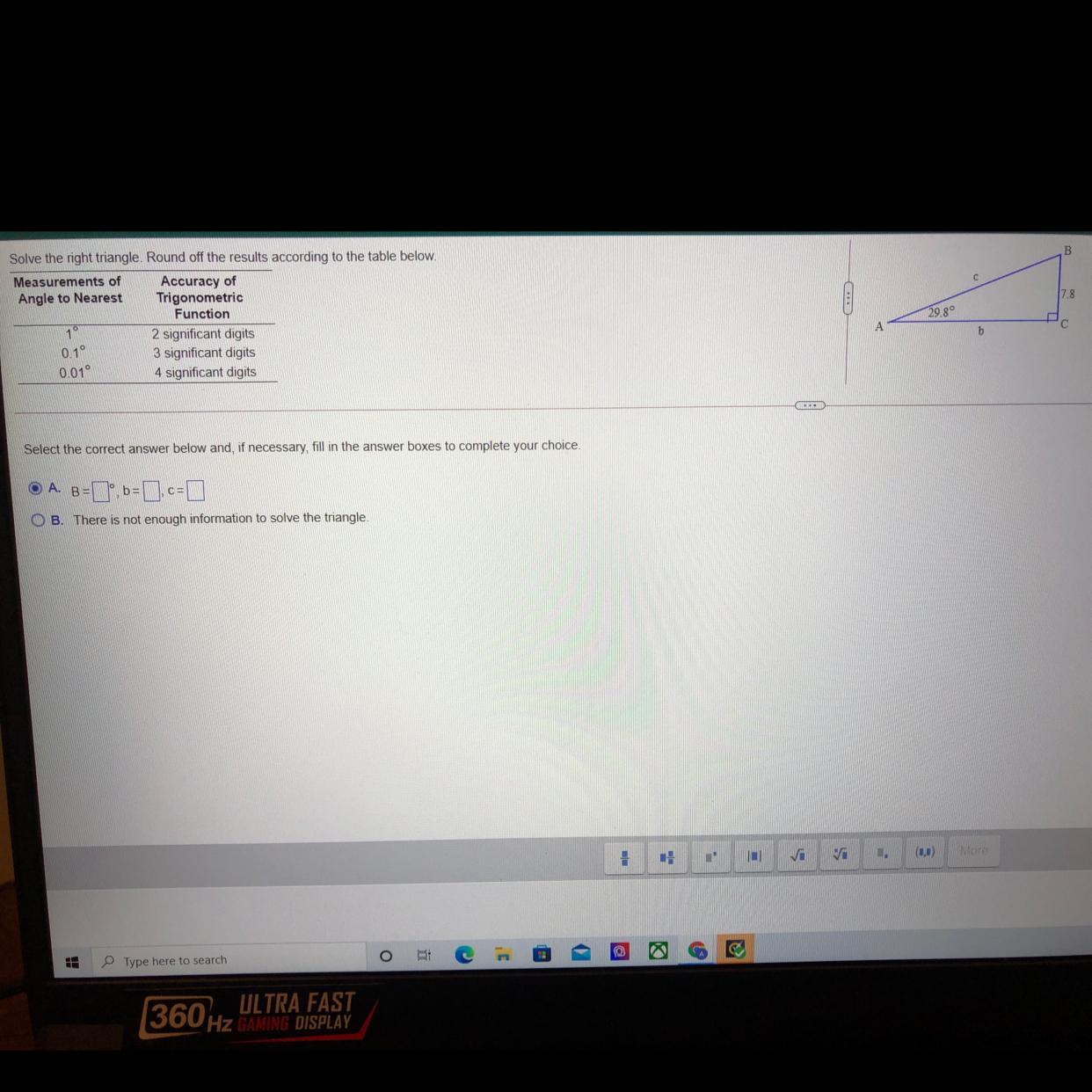
Here we have the following right triangle:
Let's find the side "b" first.
We could use the trigonometric ratio: "tan(a)". Where "a" is an angle.
The ratio tan(a), represents the relation between the opposite side of the angle and its adjacent side.
So, we could write:
\(\tan (29.8)=\frac{7.8}{b}\to b=\frac{7.8}{\tan (29.8)}=13.6\)Therefore, b=13.6
The side "c" can be found if we apply the function sin(a). Where "a" represents an angle. This ratio relations the opposite side of the angle "a" and the hypotenuse of the triangle. Then, we could write:
\(\sin (29.8)=\frac{7.8}{c}\to c=\frac{7.8}{\sin(29.8)}\to c=15.7\)Therefore, c=15.7
Finally, to find the angle B we could use the fact that the sum of all internal angles of a triangle is always 180°. Therefore, we could write:
\(\begin{gathered} 29.8+90+B=180 \\ B=180-90-29.8 \\ B=60.2 \end{gathered}\)The angle B measures 60.2°.
Related Questions
What is the inverse of the function g(x)=7x+3/x-5?
Answers
Answer:
g(x) = (5x + 3)/ x - 7
Step-by-step explanation:
Let g(x) = y
y = (7x + 3)/x - 5
Make x the subject
xy - 5y = 7x + 3
xy - 7x = 5y + 3
x(y - 7) = 5y + 3
x = (5y + 3)/ y - 7
Therefore, the inverse of the function = (5x + 3)/ x - 7
What is the solution to the equation -0.2(x - 20) = 44 - x? x = -90 x = 50 x = -50 x = 90
Answers
Answer:
x= 50
Step-by-step explanation:
First, simplify the equation
Expand the terms on the left hand side to make it easier to rearrange
-0.2(x-20) =44-x
-0.2x+4 =44-x
Rearrange the equation by moving the numbers to one side and the variables to the other
-0.2x +x= 44-4
0.8x = 40
Isolate for x
x= 40/0.8
x= 50
how to round 11,295 to the nearest ten thousand?
Answers
Given the following definitions: U = {1, 2, 3, 4, 5, 6, 7} A = {1, 2, 4, 5} B = {1, 3, 5, 7} How many elements are in A ∪ B' ? Your Answer:
Answers
Consequently, there are 5 elements in A B'.
Given the following definitions:
U = {1, 2, 3, 4, 5, 6, 7}A = {1, 2, 4, 5}B = {1, 3, 5, 7}
The complement of a set B is the set of all elements that belong to the universal set U but not to B.
A’ = {x | x ∈ U and x ∉ A} = {3, 6, 7}B’ = {x | x ∈ U and x ∉ B} = {2, 4, 6}
The union of sets A and B is the set of all elements that belong to set A or set B, or both.
A ∪ B = {x | x ∈ A or x ∈ B}
= {1, 2, 3, 4, 5, 7}A ∪ B'
= {x | x ∈ A or x ∈ B’}
= {1, 2, 4, 5, 6}
Therefore, the number of elements in A ∪ B' is 5.
To learn more about : elements
https://brainly.com/question/25916838
#SPJ8
A store pays $40 for a handbag and marks the price up by 50%. What is the amount of the mark-up?
Answers
Answer: The amount of the mark up is 20$
Step-by-step explanation:
find 50 percent of the 40
50 percent is the same as 0.5
0.5*40=20
factoring / gcf ??? (in picture)
got really sick and missed a bunch of school, would really appreciate the help !

Answers
Step-by-step explanation:
hope this will help you....


Suppose that x and y vary inversely, and x = 30 when y = 2. Find y when x=5.
Answers
Answer:
Step-by-step explanation:
1. x is inversely proportional to y
x=k/y
k is the constant of proportionality
x =60/y
2. x=60/y
x=60/12
x=5
I need help asap plz
Answers
Answer:
what's your question sir
Step-by-step explanation:
comment on this
How many people were surveyed in the bar graph 9 30 18 25

Answers
Answer:
30
Step-by-step explanation:
9 + 9 + 6 + 5 + 1 = 30
Angle TLN equals (3X -18)°, angle MZQ equals (5X +14)° and

Answers
For the given figure, x = 23° and y = 129°
Parallel lines:
Parallel lines are lines that always stay the same distance apart and never meet.
Transversal line :
A transversal is a line that crosses two or more other lines.
given,
∠TLN = (3x - 18)°
∠MZQ = (5x + 14)°
∠NLM = y°
Now,
∠MZP + ∠MZQ = 180° (Linear Pair)
∠MZP = 180° - ∠MZQ ...........(I)
again,
∠NLM + ∠TLN =180° ...........(II) (Linear Pair)
As, ∠TLN = ∠MZP (Corresponding Angle)
(3x - 18)° = 180° - ∠MZQ
(3x - 18)° = 180° - (5x + 14)°
3x + 5x = 180° - 14° + 18°
8x = 184°
x = 184 / 8
x = 23°
From (II),
∠NLM + ∠TLN =180°
y° + 3x - 18° = 180°
y = 180 - 3x + 18
= 180 - 3* 23 + 18
= 180 - 69 +18
y = 129°
For the given figure,
x = 23° and y = 129°
To learn more about Parallel line visit:
https://brainly.com/question/17432060
#SPJ9
If n = 240 and
ˆ
p
(p-hat) = 0.4, construct a 90% confidence interval.
Give your answers to three decimals
Answers
The 90% confidence interval is approximately (0.35, 0.45) or 0.35 to 0.45, rounded to three decimal places.
To construct a confidence interval with a known value of ˆp (p-hat) and a given level of confidence, we can use the formula:
Confidence Interval = ˆp ± z * √((ˆp * (1 - ˆp)) / n)
Where:
ˆp is the sample proportion (0.4 in this case)
z is the critical value associated with the desired level of confidence (90% confidence level corresponds to z = 1.645 for a large sample size)
n is the sample size (240 in this case)
Let's calculate the confidence interval:
Confidence Interval = 0.4 ± 1.645 * √((0.4 * (1 - 0.4)) / 240)
Calculating the value inside the square root:
√((0.4 * (1 - 0.4)) / 240) ≈ 0.031
Substituting the values into the confidence interval formula:
Confidence Interval = 0.4 ± 1.645 * 0.031
Calculating the values:
Lower bound = 0.4 - (1.645 * 0.031) ≈ 0.35
Upper bound = 0.4 + (1.645 * 0.031) ≈ 0.45
Therefore, the 90% confidence interval is approximately (0.35, 0.45) or 0.35 to 0.45, rounded to three decimal places.
for such more question on confidence interval
https://brainly.com/question/14771284
#SPJ8
A cereal company wants to create a box that a volume that is double the size of its
original box. Which of the following could be used to double the volume?
Answers
plz helpp
Statement 2)
A)Addition property
B) Definition of midpoint
C) Definition of equality
D) Segment addition postulate
Reason 6)
A) Subtraction property
B) Transitive property
C) Property of equality
D) Definition of congruence

Answers
Answer:
Addition Property of Equality If AB = CD then AB + BC = BC +CD
Subtraction Property of Equality If AB + BC = BC + CD then AB = CD
Multiplication Property of Equality If m∢A = 90 then 2(m∢A) = 180
Division Property of Equaliity If 2(m∢B) = 180 then m∢B = 90
Substitution Property If m∢A + m∢B =180 and m∢B then m∢A + 90 =180
Distributive Property AB + AB = 2AB
Reflexive Property m∢B = m∢B
Symmetric Property If AB + BC = AC then AC = AB + BC
Transitive Property If AB ≅ BC and BC ≅ CD then AB ≅ CD
Segment Addition Postulate If C is between B and D, then BC + CD = BD
Angle Addition Postulate If D is a point in the interior of ∢ABC then m∢ABD + m∢DBC = m∢ABC
Linear Pair Postulate If two angles form a linear pair, then they are supplementary
Definition of Right Angle If ∢B is a right angle then m∢B = 90
Definition of Midpoint If P is the midpoint of segment AB then AP =PB
Definition of Segment Bisector If k intersects segment AB at M the Midpoint then k bisects segment AB
Definition of Perpendicular Lines If two lines are ⊥ they form right angles
Definition of Congruent Segments If AB = CD then segment AB ≅ segment CD
Definition of Congruent Angles If ∡A ≅∡ B then m∡A=m∡B
Definition of Angle Bisector If ray AB bisects ∡CAD then∡ CAB ≅ ∡ BAD
Definition of Complementary Angles If ∡ Z and ∡Y are complementary m∡Z +m∡Y =90
Definition of Supplementary Angles If ∡ S and ∡T are supplementary m∡S +m∡T = 180
Step-by-step explanation:
Which of the following could be the ratio between the lengths of the two legs
of a 30-60-90 triangle?
Check all that apply.
A. √2:2
B. √√3:√√3
C. √5:3
D. 1 √3
□ E. 1: √2
O F. 2:3
SUBMIT
Answers
Answer: E
Step-by-step explanation:
Three cube-shaped boxes are stacked one above the other. The volumes of two of the boxes are 1,331 cubic meters each, and the volume of the third box is 729 cubic meters. What is the height of the stacked boxes in meters?
A.
19
B.
29
C.
30
D.
31
Answers
Answer:
D. 31
Step-by-step explanation:
The edge dimension of a cube is the cube root of the volume. For the two boxes that are 1331 m³, the height is ...
∛(1331 m³) = 11 m
For the box that is 729 m³, the height is ...
∛(729 m³) = 9 m
Then the total height of the stack of boxes is ...
11 m + 11 m + 9 m = 31 m
Answer:
31
Step-by-step explanation:
I took the test on Edmentum, have a good day hope it helps :)

By visual inspection, determine the best-fitting regression model for the
scatterplot

Answers
By visual inspection, determine the best-fitting regression model for the scatterplot is Quadratic.
We are given the scatter plot representing data.
Now, it is required to find the best regression model for the scatter plot.
From the graph, we see that,
The scatter plot has a behavior similar to a quadratic equation.
That is, the graph is starting and ending in the same direction.
Also, the points in the scatter plot are increasing at first to reach a maximum value and then decrease.
Thus, we have, Visually the scatter plot represents a quadratic equation.
What is a Quadratic equation?
In algebra, a quadratic equation is any equation that can be rearranged in standard form as where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0. If a = 0, then the equation is linear, not quadratic, as there is no term.
Learn more about quadratic equations here: https://brainly.com/question/17177510
#SPJ9
Carlo and Anita make mailboxes and toys in their wood shop. Each mailbox requires 1 hour of work from Carlo and 4 hours from Anita. Each toy requires 1 hour of work from Carlo and 1 hour from Anita. Carlo cannot work more than 12 hours per week and Anita cannot work more than 24 hours per week. If each mailbox sells for $10 and each toy sells for $5, then what is their maximum possible revenue
Answers
Answer:
$80
Step-by-step explanation:
Let the number of hours required to make a mailbox = x
Let the number of hours required to make a toy = y
Each mailbox requires 1 hour of work from Carlo and 4 hours from Anita.
Each toy requires 1 hour of work from Carlo and 1 hour from Anita.
The table below summarizes the information for ease of understanding.
\(\left|\begin{array}{c|c|c|c}&$Mailbox(x)&$Toy(y)&$Maximum Number of Hours\\--&--&--&------------\\$Carlo&1&1&12\\$Anita&4&1&24\end{array}\right|\)
We have the constraints:
\(x+y \leq 12\\4x+y \leq 24\\x \geq 0\\y \geq 0\)
Each mailbox sells for $10 and each toy sells for $5.
Therefore, Revenue, R(x,y)=10x+5y
The given problem is to:
Maximize, R(x,y)=10x+5y
Subject to the constraints
\(x+y \leq 12\\4x+y \leq 24\\x \geq 0\\y \geq 0\)
The graph is plotted and attached below.
From the graph, the feasible region are:
(0,0), (6,0), (4,8) and (0,12)
At (6,0), 10x+5y=10(6)+5(0)=60
At (4,8), 10(4)+5(8)=80
At (0,12), 10(0)+5(12)=60
The maximum revenue occurs when they use 4 hours on mailboxes and 8 hours on toys.
The maximum possible revenue is $80.

Miguel is designing shipping boxes that are rectangular prisms. One shape of the box with height h in feet, has a volume defined by the function V(h)=h(h-10(h-8). What is the height that would produce the maximum volume for the domain 0
Answers
Answer: 105ft^3
Step-by-step explanation:
Answer:
\(105ft^{3}\)
Step-by-step explanation:
V(h) = h(–h + 10)(–h + 8)
Apply the distributive property to the right side and simplify.
V(h) = h(–h + 10)(–h + 8)
V(h) = {h(-h) + h(10)}(-h+8)
V(h) = (-h²+10h)(-h+8)
V(h) = (-h²)(-h) + (-h²)(8) + (10h)(-h) + (10h)(8)
V(h) = -8h² -10h² + 80h
V(h) = -18h² + 80h
Plug in the value of h from 1 to 9 (since 0<h<10) into the function V(h) = -18h² + 80h and create a table
h | V(h)
1 | 63
2 | 96
3 | 105 <------maximum volume is the highest y-value
4 | 96
5 | 75
6 | 48
7 | 21
8 | 0
9 | -9
The maximum volume for the domain 0<h<10 is 105 cubic feet.
A line with a slope of 14/3 passes through the point (0,8). What is the equation in slope-intercept form?
Write your answer using integers, proper fractions, and improper fractions in simplest form.

Answers
The equation of slope-intercept form of the line is y = 14/3x + 8.
What is in slope-intercept form?
Given the slope of the line and the intercept it forms with the y-axis, one of the mathematical forms used to derive the equation of a straight line is called the slope intercept form. Y = mx + b, where m is the slope of the straight line and b is the y-intercept, is the slope intercept form.Given,
m = 14/3
the point = ( 0,8 )
A line with a slope of 14/3 passes through the point (0,8).
y - y₁ = m ( x- x₁)
y - 8 = 14/3 ( x - 0 )
3(y - 8 ) = 14x
3y - 24 = 14x
3y = 14x + 24
y = 14/3x + 8
Finally, the equation of the line is
y = 14/3x + 8
Learn more about slope-intercept form
brainly.com/question/9682526
#SPJ9
the temperatures for the first 10 days of January were recoded as follows 22 43 47 8 51 39 35 50 28 and 43 sara is organizing the temperatures to the display on a stem and leaf plot what will the stems be for the display
A. 0, 1, 2, 3, 5, 7, 8, 9
B. 0, 1, 2, 3, 4, 5
C. 0, 2, 3, 4, 5
D. 2, 3, 4, 5
Answers
is there a picture
Please put one so i. can help
.
-0.125 as a fraction
Answers
Answer:
-1/8
Step-by-step explanation.
125 x 8 = 1000
.125 x 8 = 1
-.125 x 8 = -1
-1/8
The solution to a quadratic are called
Answers
Answer:
roots
Step-by-step explanation:
A quadratic equation with real or complex coefficients has two solutions, called roots.
Roots are also called x-intercepts or zeros. ... The roots of a function are the x-intercepts. By definition, the y-coordinate of points lying on the x-axis is zero. Therefore, to find the roots of a quadratic function, we set f (x) = 0, and solve the equation, ax2 + bx + c = 0.
what is 11/4 times 4/9
Answers
Answer: 11/9
Step-by-step explanation:
you would cross out the two 4s(using butterfly method) and make them 1s. So 11 x 1 and 1 x 9 = 11/9
Answer:
11/4 times 4/9 is 11/9
Step-by-step explanation:
We have to find,
(11/4) times 4/9
\((11/4)(4/9) = (11*4/4*9)\)
We can cancel the 4s from the numeratorand denominator to get,
\((11*4/4*9) = (11*1/1*9) = 11/9\\=11/9\)
The answer is 11/9
Lilah invested $400 in the stock market. She saw an 8% decrease in her money, what is the value of her stocks now
Answers
The value of Lilah's stock after the decrease of 8 % is $ 368
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the initial amount of money Lilah invested in stocks be = A
The value of A is = $ 400
Now , the percentage decrease in the value of stocks = 8 %
So , the equation will be
The value of the stocks after the decrease = initial amount of money Lilah invested in stocks - ( percentage decrease in the value of stocks x initial amount )
Substituting the values in the equation , we get
The value of the stocks after the decrease = 400 - ( 8/100 ) x 400
The value of the stocks after the decrease = 400 - ( 8 x 4 )
The value of the stocks after the decrease = 400 - 32
The value of the stocks after the decrease = $ 368
Therefore , the value of A is $ 368
Hence , The value of Lilah's stock after the decrease of 8 % is $ 368
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
A survey of 70 people found that 50 people like coffee, 25 like tea, and 13 like both.How many people like coffee or tea, or both?
Answers
Step-by-step explanation:
your question is strange.
first you tell us that 50 people like coffee, 25 like tea, and 13 like both.
and then you ask how many like coffee or tea or both.
is this a joke ? or do you rather mean how many like only coffee, or only tea, and how many don't like neither ?
since 13 people like coffee and tea, these 13 are also part of the group of 50 that like coffee, and of the group of 25 that like tea.
so, to get the number of people that like only one, we need to deduct the number of people, who like both from both groups.
the number of people that only like coffee is therefore
50 - 13 = 37
and the number of people that only like tea is
25 - 13 = 12
we know the number of people that like coffee and tea is 13.
together that are
37 + 12 + 13 = 62 people.
that means 70 - 62 = 8 people don't like neither coffee nor tea.
Answer: 62
Step-by-step explanation:
Those who like coffee only = 50 - 13 = 37. Those who like tea only = 25 - 13 = 12. Those who like either coffee, or tea, or both = 37 + 12 + 13 = 62.
In theory, the 70 people being surveyed could fall under any of the following four categories:
Those who like coffee,Those who like tea,Those who like both coffee and tea,Those who like neither coffee nor tea.I have labelled the four categories 1, 2, 3 and 4 for convenient reference.
From the information provided in the question, category 1 contains 50 people, category 2 contains 25 people, while category 3 contains 13 people. We do not yet know how many people fall under category 4, but we shall calculate it.
We know from set theory that the four aforementioned categories are known formally as sets. A set is simply a group of objects or things that are similar in some way. Each of the objects in a set is called a member of that set. Two sets can intersect. The intersection of two sets is simply the collection of members that are in both of the two sets. Also, two sets can unite. The union of two sets is the collection of members that in either of the two sets.
For example, category 3 is the intersection of category 1 and 2. The question requires us to calculate the union of category 1 and 2.
What are the points of the image of the line in Q4 after the dilation?

Answers
Note that the coordinates of the point A' after rotating 90 degrees clockwise about the point (0,1) are (3, -4). (Option B)
How is this so ?To rotate a point 90 degrees clockwise about a given point,we can follow these steps -
Translate the coordinates of the given point so that the center of rotation is at the origin. In this case,we subtract the coordinates of the center (0,1) from the coordinates of point A (5,4) to get (-5, 3).
Perform the rotation by swapping the x and y coordinates and changing the sign of the new x coordinate. In this case,we swap the x and y coordinates of (-5, 3) to get (3, -5).
Translate the coordinates back to their original position by adding the coordinates of the center (0,1) to the result from step 2. In this case, we add (0,1) to (3, -5) to get (3, -4).
Therefore, the coordinates of the point A' after rotating 90 degrees clockwise about the point (0,1) are (3, -4).
Learn more about coordinates at:
https://brainly.com/question/17206319
#SPJ1
find the value of x and the measure of angle axc

Answers
Answer:
x = 4
m<AXC = 150
Step-by-step explanation:
m<1 + m<2 = m<AXC
102 + 10x + 8 = 6(6x + 1)
10x + 110 = 36x + 6
26x = 104
x = 4
m<AXC = 6(6x + 1)
m<AXC = 6(24 + 1)
m<AXC = 150
If and is in , find cos

Answers
Answer:
9/41
Step-by-step explanation:
Draw a right triangle in quadrant 2 and label your opposite (40) and hypotenuse (41) sides then use the pythagorean theorem to find the missing side (the adjacent side) which is equal to 9. Then since cosine is adjacent/hypotenuse and you get 9/41.
I need help asappppppp

Answers
Answer:150?
Step-by-step explanation:
At noon, ship A is 40 miles due west of ship B. Ship A is sailing west at 24 mph and ship B is sailing north at 22 mph. How fast (in mph) is the distance between the ships changing at 4 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)
Answers
Answer:
\(32.10\ \text{mph}\)
Step-by-step explanation:
Distance traveled by A in 4 hours = \(24\times 4=96\ \text{mi}=a\)
Distance traveled by B in 4 hours = \(22\times 4=88\ \text{mi}=b\)
Total distance between A and the initial point of B is \(40+96=136\ \text{mi}\)
Distance between A and B 4 hours later
\(c=\sqrt{136^2+88^2}\ \text{mi}\)
From Pythagoras theorem we have
\((a+40)^2+b^2=c^2\)
Differentiating with respect to time we get
\(2(a+40)\dfrac{da}{dt}+2b\dfrac{db}{dt}=2c\dfrac{dc}{dt}\\\Rightarrow (a+40)\dfrac{da}{dt}+b\dfrac{db}{dt}=c\dfrac{dc}{dt}\\\Rightarrow \dfrac{dc}{dt}=\dfrac{(a+40)\dfrac{da}{dt}+b\dfrac{db}{dt}}{c}\\\Rightarrow \dfrac{dc}{dt}=\dfrac{(96+40)\times24+88\times 22}{\sqrt{136^2+88^2}}\\\Rightarrow \dfrac{dc}{dt}=32.10\ \text{mph}\)
So, the the distance between the ships at 4 PM is changing at \(32.10\ \text{mph}\)
