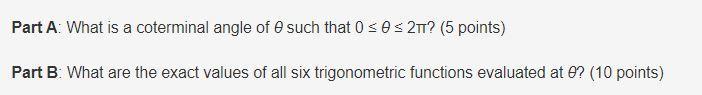Answers
So,
Given
\(\theta=-\frac{11\pi}{4}\)We could draw this angle:
A coterminal angle between 0 ans 2pi for the given angle is 5pi/4.
Related Questions
f(x) = 1/2 (x-8) -6
Answers
Inverse of this equation is 2x+20. Or
X intercepts: (20,0) Y intercepts: (0,-10)
Answer:
where's the question? I dog understand
(a) Find the lateral area (in square inches) of the prism.
(b) Find the total area (in square inches) of the prism.
(c) Find the volume (in cubic inches) of the prism.

Answers
Answer:
c
Step-by-step explanation:
Among coffee drinkers, men drink a mean of 3.2 cups per day with a standard deviation of 0.8 cups. Assume the number of cups per day follows a normal distribution.
a. What proportion drink 2 cups per day or more?
b. What proportion drink no more than 4 cups per day?
c. If the top 5% of coffee drinkers are considered "heavy" coffee drinkers, what is the minimum number of cups consumed by a heavy coffee drinker?
d. If a sample of 20 men is selected, what is the probability that the mean number of cups per day is greater than 3?
Answers
Answer:
a) 0.9332 = 93.32% drink 2 cups per day or more.
b) 0.8413 = 84.13% drink no more than 4 cups per day
c) The minimum number of cups consumed by a heavy coffee drinker is 4.52.
d) 86.86% probability that the mean number of cups per day is greater than 3
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal probability distribution
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question, we have that:
\(\mu = 3.2, \sigma = 0.8\)
a. What proportion drink 2 cups per day or more?
This is 1 subtracted by the pvalue of Z when X = 2. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{2 - 3.2}{0.8}\)
\(Z = -1.5\)
\(Z = -1.5\) has a pvalue of 0.0668
1 - 0.0668 = 0.9332
0.9332 = 93.32% drink 2 cups per day or more.
b. What proportion drink no more than 4 cups per day?
This is the pvalue of Z when X = 4.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{4 - 3.2}{0.8}\)
\(Z = 1\)
\(Z = 1\) has a pvalue of 0.8413
0.8413 = 84.13% drink no more than 4 cups per day
c. If the top 5% of coffee drinkers are considered "heavy" coffee drinkers, what is the minimum number of cups consumed by a heavy coffee drinker?
This is the 100 - 5 = 95th percentile, which is X when Z has a pvalue of 0.95. So X when Z = 1.645. Then
\(Z = \frac{X - \mu}{\sigma}\)
\(1.645 = \frac{X - 3.2}{0.8}\)
\(X - 3.2 = 1.645*0.8\)
\(X = 4.52\)
The minimum number of cups consumed by a heavy coffee drinker is 4.52.
d. If a sample of 20 men is selected, what is the probability that the mean number of cups per day is greater than 3?
Sample of 20, so applying the central limit theore with n = 20, \(s = \frac{0.8}{\sqrt{20}} = 0.1789\)
This probability is 1 subtracted by the pvalue of Z when X = 3.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{3 - 3.2}{0.1789}\)
\(Z = -1.12\)
\(Z = -1.12\) has a pvalue of 0.1314
1 - 0.1314 = 0.8686
86.86% probability that the mean number of cups per day is greater than 3
HELP PLS !% POINTS!!

Answers
Answer:
149 sq. ft
Step-by-step explanation:
For the triangle:
Base = 16-9 = 7 ft
Area of Triangle = 1/2 of b.h
= 1/2 of 7 * 6
= 21 sq. ft
Area of Rectangle = l.b
= 5 * 16
= 128 sq. ft
Total Area = 149 sq. ft
Giving brainlist so plzzzz help its a test
You flip a fair coin.
What is P(heads)
If necessary, round your answer to 2 decimal places.
Answers
If y is inversely proportional to the square root of x and y=−70 when x=49, find y if x=2401.
Answers
The value of y when x= 2401 is -10
How to determine the value of x?An inverse variation is represented as:
\(y = \frac{k}{\sqrt x}\)
Where k is the proportionality constant
When y = -70, x = 49
So, we have:
\(-70 = \frac{k}{\sqrt {49}}\)
Take the square root of 49
\(-70 = \frac{k}{7}\)
Multiply through by 7
k = -490
Substitute k = -490 in \(y = \frac{k}{\sqrt x}\)
\(y = -\frac{490}{\sqrt x}\)
When x =2401, we have
\(y = -\frac{490}{\sqrt {2401}}\)
Evaluate the square root
\(y = -\frac{490}{49}\)
Divide
y = -10
Hence, the value of y when x= 2401 is -10
Read more about variation at:
https://brainly.com/question/14254277
#SPJ1
A copy machine makes 143 copies in 3 minutes and 15 seconds. How many copies does it make per minute?
I copies per minute
?
Answers
143/3.25 = 44
Sets Sets M and Fare defined as follows: M = {a,b,c,d} F = {c, d, e, f} Find the intersection of M and F.
Answers
The intersection of sets M and F contains the elements "c" and "d".
To find the intersection of sets M and F, we need to identify the elements that are common to both sets.
M = {a, b, c, d}
F = {c, d, e, f}
The intersection of M
and F is denoted by M ∩ F, which represents the set containing elements that are present in both M and F.
Looking at the elements in M and F, we can see that the common elements between the two sets are "c" and "d".
Therefore, the intersection of M and F can be expressed as:
M ∩ F = {c, d}
So, the intersection of sets M and F contains the elements "c" and "d".
for such more question on intersection
https://brainly.com/question/11337174
#SPJ8
The fence around a circular pool is 75 ft long.
Radius=
Diameter=
Circumference=
Answers
Answer:
Step-by-step explanation:
circumference=75 ft.
2πr=75
r=75/2π=75/(2×3.14)≈11.937
radius=11.94 ft
Diameter=2r=2×11≈23.87 ft
The curvature of a circle is inversely proportional to its radius. What is the exact circumference of a circle with one-third the curvature of a circle of radius 1?
Answers
The circumference of a circle with one-third the curvature of a circle of radius 1 is 18.85 units
What is circumference ?
The perimeter of a circle is known as its circumference. It is the length of the circle's whole perimeter. The diameter of a circle and the constant are multiplied to get the circumference of the circle. This measurement of a circle's circumference is necessary for someone to cross a circular park or for a circle-shaped table to have a border. The units of the circumference are the same as the units of length and it is a linear value.
If a circle has a radius of 1,
the curvature is inversely proportional to this
So, the curvature= 1
A circle with a curvature of 1/3 :
radius=3
Thus, the circumference of the circle = 2 *π * radius
= 2*π * 3
= 6π
≈ 18.85 units
To learn more about the circumference from the given link
https://brainly.com/question/20489969
#SPJ1
1. Dicey Odds [2 Points]You roll two six-sided dice. Die 1 is fair. Die 2 is unfair such that the probability of rolling anodd number is23and the probability of rolling an even number is13, though the probabilityrolling of each odd number is the same, and the probability of rolling each even number isthe same. What is the probability of:a) rolling a number less than 4 on Die 1 and rolling a 5 on Die 2.b) the sum of both dice adding up to 4.
Answers
Answer:
a) P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) = \(\frac{1}{9}\)
b) P( the sum of both dice adding up to 4) = \(\frac{5}{54}\)
Step-by-step explanation:
Given - You roll two six-sided dice. Die 1 is fair. Die 2 is unfair such that the probability of rolling an odd number is \(\frac{2}{3}\) and the probability of rolling an even number is \(\frac{1}{3}\) , though the probability rolling of each odd number is the same, and the probability of rolling each even number is the same.
To find - What is the probability of:
a) rolling a number less than 4 on Die 1 and rolling a 5 on Die 2.
b) the sum of both dice adding up to 4.
Proof -
The sample space , S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
Now,
Given that , Dice 1 is fair
⇒P₁(1) = P₁(2) = P₁(3) = P₁(4) = P₁(5) = P₁(6) = \(\frac{1}{6}\)
Also, Given Dice 2 is unfair
⇒P₂(1) = P₂(3) = P₂(5) = \(\frac{2}{3}.\frac{1}{3} = \frac{2}{9}\)
P₂(2) = P₂(4) = P₂(6) = \(\frac{1}{3}.\frac{1}{3} = \frac{1}{9}\)
Now,
a)
P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) = P₁(1)P₂(5) + P₁(2)P₂(5) + P₁(3)P₂(5)
= P₂(5) [ P₁(1) + P₁(2) + P₁(3) ]
= \(\frac{2}{9}\) [ \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) ] = \(\frac{2}{9}[ \frac{3}{6}]\\\) = \(\frac{1}{9}\)
⇒P(rolling a number less than 4 on Die 1 and rolling a 5 on Die 2) = \(\frac{1}{9}\)
b)
P( the sum of both dice adding up to 4) = P₁(1)P₂(3) + P₁(2)P₂(2) + P₁(3)P₂(1)
= \(\frac{1}{6}\) × \(\frac{2}{9}\) + \(\frac{1}{6}\) × \(\frac{1}{9}\) + \(\frac{1}{6}\) ×\(\frac{2}{9}\) = \(\frac{5}{54}\)
⇒P( the sum of both dice adding up to 4) = \(\frac{5}{54}\)
Recall that with base-ten blocks: 1 long 10 units, 1 flat 10 longs, and 1 block 10 flats. What is the fewest number of multibase blocks that can be used to represent the corresponding numeral in the given base?
a. 20 longs in base seven
b. 10 longs in base three
Answers
a. The answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. The answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
a. To represent 20 longs in base seven, we need to find the fewest number of multibase blocks required.
In base seven, we have the following conversions:
1 long = 1 unit
1 flat = 10 units
1 block = 10 flats
To represent 20 longs, we can use 2 flats (each flat representing 10 units) and 0 units since there are no remaining units.
So, the fewest number of multibase blocks required would be 2 flats.
Therefore, the answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. To represent 10 longs in base three, we need to find the fewest number of multibase blocks required.
In base three, we have the following conversions:
1 long = 1 unit
1 flat = 3 units
1 block = 3 flats
To represent 10 longs, we can use 3 flats (each flat representing 3 units) and 1 unit since there is one remaining unit.
So, the fewest number of multibase blocks required would be 3 flats and 1 unit.
Therefore, the answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
for such more question on fewest number
https://brainly.com/question/859564
#SPJ8
2 planes left an airport at 10:30 am.one travelled due south at an average speed of 400km and the second travelled due east at an average speed 300km per hour .how far apart when the two planes at 2:30 pm
Answers
Therefore , the solution of the given problem of speed comes out to be average speed of the aeroplane = 200 km/h.
What is speed ?An object's velocity, as opposed to its speed, describes how quickly it goes in both directions. Velocity in physics is the rate of movement in a specific direction. A car's speed is described when we say it goes at 60 km/h.
Here,
Speed of the aeroplane for 400 km = = (400/2) = 200 km/h (due north)
Speed of the aeroplane = 300 km/h (due east)
Speed is a scalar quantity. So no direction is needed. Just for question, direction is given here, for understanding purpose.
Average speed of the aeroplane = (200 + 300)/2
= 250 km/h
Therefore , the solution of the given problem of speed comes out to be average speed of the aeroplane = 200 km/h.
To know more about speed , visit
https://brainly.com/question/7359669
#SPJ1
Answer:
2000km
Step-by-step explanation:
To find the distance between the two planes at 2:30 pm, we need to determine the positions of each plane at that time.
Since the first plane traveled due south at an average speed of 400 km/h for 4 hours (from 10:30 am to 2:30 pm), it would have covered a distance of 400 km/h * 4 h = 1600 km due south.
Similarly, the second plane traveled due east at an average speed of 300 km/h for 4 hours, covering a distance of 300 km/h * 4 h = 1200 km due east.
To find the distance between the two planes, we can use the Pythagorean theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.
In this case, the distance between the two planes represents the hypotenuse of a right triangle, with the southward distance traveled by the first plane as one side and the eastward distance traveled by the second plane as the other side.
Using the Pythagorean theorem:
Distance^2 = (1600 km)^2 + (1200 km)^2
Distance^2 = 2,560,000 km^2 + 1,440,000 km^2
Distance^2 = 4,000,000 km^2
Taking the square root of both sides to find the distance:
Distance = √4,000,000 km^2
Distance ≈ 2000 km
Therefore, the two planes are approximately 2000 km apart at 2:30 pm.
Which expression is equivalent to 250 + 150 ?
Answers
Answer:
if 25c + 15d = 0, then d = -25/15c
Step-by-step explan
just yes, that
a rectangular auditorium seats 2244 people. The number of seats in each row exceeds the number of rows by 7. Find the number of seats in each row
Answers
Number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7. This can be obtained by assuming the value of number of seats in each row, forming quadratic equation and using quadratic formula to find root.
Find the number of seats in each row:
Here in the question it is given that,
a rectangular auditorium seats 2244 peoplenumber of seats in each row exceeds the number of rows by 7We have to find the number of seats in each row.
Let us assume that the number of seats in each row be x.
From the given statement, number of seats in each row exceeds the number of rows by 7, we can write that,
Number of seats in one row = Number of rows + 7
x = Number of rows + 7
⇒ Number of rows = x - 7
Total number of seats in the auditorium can be written as,
⇒ (Number of seats in one row)(Number of rows) = Total number of seats
(x)(x - 7) = 2244
x² - 7x = 2244
⇒ x² - 7x - 2244 = 0
By using quadratic formula we can find the root,
x = (-b ± √b² - 4ac)/2a
here in the question, a = 1, b = -7, c = -2244
√b² - 4ac = √(-7)² - 4(1)(-2244)
√b² - 4ac = √49 + 8976
√b² - 4ac = √9025
√b² - 4ac = 95
x = (-b ± √b² - 4ac)/2a
x = (7 ± 95)/2
x = 102/2 or x = -88/2
⇒ x = 51 or x = -44
Hence number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7.
Learn more about quadratic formula here:
brainly.com/question/26926523
#SPJ9
what are product rule
Answers
The rule may be extended or generalized to products of three or more functions, to a rule for higher-order derivatives of a product, and to other contexts.
Given that cosθ=817 and sinθ=−1517 . What is the value of tanθ?
Answers
Answer:
tan∅ = -1517/817
Step-by-step explanation:
tan∅ = sin∅/cos∅
Answer:
Step-by-step explanation:

The cost of a newspaper subscription
includes a discounted initial week. Beatriz
pays $55 for 7 weeks of the newspaper
subscription and $100 for 12 weeks.
Answers
As a result, the original discounted price is $1 while the weekly normal price is $9.
How does arithmetic work with discounts?The fundamental formula for calculating a reduction is to increase the initial price by the provided percentage rate in decimal form. We must deduct the reduction from the initial price to determine the item's sale price.
From the given information, we have:
d + 6x = 55 (discounted price for 7 weeks)
d + 11x = 100 (discounted price for 12 weeks)
We can solve this system of equations by eliminating d. Subtracting the first equation from the second, we get:
5x = 45
Dividing both sides by 5, we get:
x = 9
Substituting x = 9 into one of the equations, we can solve for d. Using the first equation, we get:
d + 6(9) = 55
d + 54 = 55
d = 1
To know more about Discount visit:
https://brainly.com/question/1548141
#SPJ1
The function m(g) provides the number of miles a car can travel on g gallons of gas. The fuel tank holds 14 gallons which allows a maximum ride of 504 miles.
What is the domain of the function?

Answers
Answer:
we conclude that the domain of 'g' should be:
0 ≤ g ≤ 14Step-by-step explanation:
We know that the domain of a function is the set of input or argument values for which the function is real and defined.Given that the function m(g) provides the number of miles a car can travel on 'g' gallons of gas.
Also, the fuel tank holds 14 gallons which allows a maximum ride of 504 miles.
As the distance covered by Car in miles is dependent on the availability of the fuel.
Thus, fuel gallons 'g' is an independent quantity and hold x-values.
Given that the fuel tank holds 14 gallons 'g'.Thus, the domain of 'g' should be:
0 ≤ g ≤ 14Therefore, we conclude that the domain of 'g' should be:
0 ≤ g ≤ 14What are the outputs of the function below?
-6, -3, 1, 5
-6, -3, 4, 6
-8, 2, 4, 6
-8, 2, 1, 5

Answers
Answer:
\(5 { \times 54}^{2} \)
FIRST ANSWER WILL GET 100 PTS!
What mixed number is equivalent to 21 ÷ 4?
Answers
Answer:
Step-by-step explanation:
5 1/4
Answer:là
5
với số dư
1
.
5
1
4
Step-by-step explanation:
HELP ASAP PLEASE THIS IS FOR ALGEBRA
1. he slope of a line through the points (-2, 4) and (6, b) is -3/2 What is the value of b?
Explain your method for calculating b.
Answers
Answer:
Step-by-step explanation:
Use the slope formula to solve this problem. Slope, usually called m, is the change in y-values over the change in x-values.
m = (y2 - y1)/(x2 -x1)
It actually doesn't matter which point is the first point and which point is the second point. But you must be consistent.
So fill in -3/2 for the m
Let your (6, b) be your (x1, y1)
Let (-2, 4) be your (x2, y2)
So, the numbers fill into the formula like so:
-3/2 = (4 - b)/ (-2 - 6)
-3/2 = (4 - b)/(-8)
Multiply -8 on both sides of the equation.
(-8)(-3/2) = 4 - b
12 = 4 - b
Subtract 4 from both sides.
Don't lose the negative in front of the b
8 = -b
Multiply or divide by -1 on both sides.
-8 = b This is the answer.
**note: Its kinda crummy to use b in this equation, because b has a special meaning when you are working with linear equations. They should have given you a different variable. b usually stands for the y-intercept but in this problem it doesn't, it's just a variable representing an unknown value.
see picture.. see picture..

Answers
Check the picture below.

For each value of v, determine whether it is a solution to v > 8.

Answers
Answer:
.
Step-by-step explanation:
PLEASE HELP ASAP!!!
A group of students must collect at least $120 to organize a science fair. They have already collected $30. Which graph best represents all remaining amounts of money, in dollars, that the students should still collect to organize the science fair? Number line graph with closed circle on 120 and shading to the right Number line graph with closed circle on 90 and shading to the right. Number line graph with closed circle on 150 and shading to the right Number line graph with closed circle on 30 and shading to the right.
Answers
Answer:
OPITON 2
Step-by-step explanation:
120-30=90 SHE NEED 90 DOLARS MORE
Select all the expressions equivalent to (4x⁵)(5x⁶).
Answers
Step-by-step explanation:
\( = 4 {x}^{5} \times 5 {x}^{6} \)
\( = (4 \times 5) {x}^{5 + 6} \)
\( = 20 {x}^{11} \)
The process of using the same or similar experimental units for all treatments is called:______
a. blocking.
b. partitioning.
c. factoring.
d. replicating.
Answers
Answer:
replicating
Step-by-step explanation:
f(x)=2x-6 g(x)=3x+9, find (f+g)
Answers
Answer:
(f+g)(x) = 5x +3
Step-by-step explanation:
(f+g)(x) = f(x) +g(x)
= (2x -6) +(3x +9)
= 2x +3x -6 +9
(f+g)(x) = 5x +3
Please help me, thanks!

Answers
Answer:
Algebraic expression for 75 less than twice Mabel's score is 2m-75
Step-by-step explanation:
We need to translate the phrase 75 less than twice Mabel's score into algebraic expression.
Translating into algebraic expression
Let m represent Mabel's score
Twice Mabel's score = 2m
75 less than Twice Mabel's score = 2m-75
So, algebraic expression for 75 less than twice Mabel's score is 2m-75
CAN SOMEONE HELP WITH THIS QUESTION?

Answers
The value of the given summation is:
\(\sum (29a_i - 13b_i) ]= -30\)
How to find the sum?Here we know that the sums are:
\(\sum a_i = -10\\\\\sum b_i = -20\)
And we want to find the value of the sum:
\(\sum (29a_i - 13b_i)\)
First we can distribute the sum to get:
\(\sum 29a_i + \sum - 13b_i\)
And take the coefficients out of the sum:
\(29\sum a_i -13\sum b_i\)
Now replace the known values:
\(29\sum a_i -13\sum b_i = 29*-10 - 13*-20 = -290 + 260 = -30\)
Learn more about sums at:
https://brainly.com/question/30518693
#SPJ1