Let X be a binomial random variable with n trials and probability p of success. A.What is the generalized likelihood ratio for testing H_0: p = .5 versus H_A: p notequalto .5? B.Show that the test rejects for large values of |X - n/2|. C.Using the null distribution of X, show how the significance level corresponding to a rejection region |X - n/2| > k can be determined. D.If n = 10 and k = 2, what is the significance level of the test? E.Use the normal approximation to the binomial distribution to find the significance level if n = 100 and k = 10.
Answers
A: p not equal to the value will be \($$N=\left(\frac{n / 2}{x}\right)^x\left(\frac{n / 2}{n-x}\right)^{n-9} .$$\)
B.Using the null distribution of X, show how the significance level corresponding to a rejection region |X - n/2| > k can be determined.
C. If n = 10 and k = 2, the significance level of the test = 0.11
D. Use the normal approximation to the binomial distribution of the significance level if n = 100 and k = 10 the value will be N(0.1).
1. The value of the generalized likelihood ratio test statistic will be
\(A=\frac{\left(\begin{array}{l}n \\x\end{array}\right)(1 / 2)^n}{m_0 x_{0 < p < 1}\left(\begin{array}{l}n \\x\end{array}\right) p^n(1-p)^{n-x}}\)
As we know, the denominate will be maximized when \($p=x / n$\), the P under \(\Omega\)
Hence \($$N=\left(\frac{n / 2}{x}\right)^x\left(\frac{n / 2}{n-x}\right)^{n-9} .$$\)
b)
\($$\begin{aligned}\Lambda & =\left(\frac{n / 2}{x}\right)^x\left(\frac{n / 2}{n-x}\right)^{n-x} \\& =\left[\left(\begin{array}{c}2 x \\n\end{array}\right)^{-2 x / n}\left(2-\frac{2 x}{n}\right)^{-2+2 x / n}\right]^{n / 2} \\& =\left[y^{-y}(2-y)^{-(2-y)}\right]^{n / 2} \\& =\left[(1+v)^{-(1+v)}(1-v)-(1-v)\right]^{n / 2}\end{aligned}$$\)
where \(y=2 x / n=1+0\)
The last expression is symmetric about \(\theta=0+\) is a maximum \($\rightarrow t v=0$\).
since the test rejects \(H_0\) when \($\wedge$\) it is small.
If the only if \($|0|=|1,2 \pi| n \mid$\) is large.
This is equivalent to |x-n/2| is large
c) The significance level \($\alpha$\) of the test that rejects H_0 when \($|x-n| 2 \mid > *$\) is given by \($$P\left(|x-n / 2| > k \mid H_0\right) \text {. }$$\)
This probability can be determined using the pmf of the B(n, 0.5) distribution.
d) If n=10+k=2,
\($$\begin{aligned}& P\left(|x-n|=| > k| H_0\right) \\= & P\left(|x-5| > 2 \mid H_0\right) \\= & P\left(x=0 \mid H_0\right)+P\left(x=1 / H_0\right)+P\left(x=2 \mid H_0\right)+P\left(x=8 / H_0\right) \\& +P\left(x=9 \mid H_0\right)+P\left(x=10\left(H_0\right)\right. \\= & 0.11 .\end{aligned}$$\)
e) Using the normal approximation to the binomial distribution B(100,0.5), x is approximately n amply distributed with mean 50 * variance n p(1-p)=25.
Thus, the significant level of the test is
\($$\begin{aligned}& P(|x-50| > 10) \approx P(|z| > 2)=0.046 . \\& \text { where } z \sim N(0,1) \text {. } \\&\end{aligned}$$\)
For such more questions on the binomial distribution
https://brainly.com/question/9325204
#SPJ4
Related Questions
The total amount of candy sold at Cassandra's Candy Corner can be represented by the function C(x) = 4x3 + 10x2 + 54x + 520, where x represents the number of years since the store opened. The amount of types of candy can be modeled by the linear function T(x) = 2x + 10. Which expression represents the amount of candy sold each year per type at Cassandra's Candy Corner?
2x^2 – 5x + 52
2x^2 + 5x + 52
4x^3 + 10x^2 + 52x + 510
4x^3 + 10x^2 + 56x + 530
Answers
Using polynomial division, it is found that the expression that represents the amount of candy sold each year per type at Cassandra's Candy Corner is:
\(2x^2 - 5x + 52\)
The amount of candy sold per type is given by the following division:
\(\frac{C(x)}{T(x)} = \frac{4x^3 + 10x^2 + 54x + 520}{2x + 10}\)
The denominator can be written as:
\(2x + 10 = 2(x + 5)\)
At the numerator, to see if we can simplify, we verify if x = -5 is a factor:
\(C(-5) = 4(-5)^3 + 10(-5)^2 + 54(-5) + 520 = 0\)
Since C(-5) = 0, it is a factor of the numerator, and thus, since the numerator is of the 3rd degree, it can be written as a 3 - 1 = 2nd degree polynomial multiplying x + 5:
\((ax^2 + bx + c)(x + 5) = 4x^3 + 10x^2 + 54x + 520\)
\(ax^3 + (5a + b)x^2 + (5b + c)x + 5c = 4x^3 + 10x^2 + 54x + 520\)
Equaling both sides:
\(a = 4\)
\(b = 10 - 5a = -10\)
\(5c = 520 \rightarrow c = 104\)
Thus:
\(C(x) = (4x^2 - 10x + 104)(x + 5)\)
And:
\(\frac{C(x)}{T(x)} = \frac{(4x^2 - 10x + 104)(x + 5)}{2(x + 5)} = 2x^2 - 5x + 52\)
Thus, the expression is:
\(2x^2 - 5x + 52\)
A similar problem is given at https://brainly.com/question/13586325
What did you include in your response? Check all that
apply.
Sample Response: Because vertical angles are
congruent, angles 1 and 4 are congruent. Because
corresponding angles are congruent, angles 4 and 8 are
congruent. Because angle 4 is congruent to both 1 and 8,
angle 1 is congruent to angle 8.
vertical angles theorem
corresponding angles theorem
transitive property
supplementary angles
linear pairs
Answers
Answer:
1. The first theorem used is that vertical angles are congruent.
2. The next theorem used is that adjacent angles in a parallelogram are supplementary.
3. The definition of supplementary angles is then used for angle formed by intersecting lines.
4. The theorem on vertical angles is used again.
5. Finally, the definition of the transitivity property is used to prove that alternate exterior angles are congruent.
Plssss helpp I’ll mark u brainliest fr

Answers
Explanation: I hope this helps
Each side length of a triangle is 4 cm. What type of triangle is it?
☐ right
□acute
Equilateral
Isosceles
Answers
Answer: Equilateral
Step-by-step explanation:
It's equilateral because it says that each side of the triangle is 4cm. In simple words, all the sides of triangle are equal. Such a triangle is called an equilateral triangle.
Hope you understood.
If a picture measures 3 inches by 5 inches and it is dilated by a scale factor of 4, the new dimensions will be ________________________________________.
A. 12 inches by 20 inches
B. 15 inches by 15 inches
C. 7 inches by 9 inches
D. 0.75 inches by 1.25 inches
Answers
Answer:
A) 12 inches by 20 inches
Step-by-step explanation:
Dilation of a scale factor means to increase by a factor of 4.
That basically mean multiply the object by 4.
Therefore 3 inches x 4 = 12 inches
And 5 inches x 4 = 20
Solve the system of equations algebraicallyy = 2x - 35x + 2y = 39
Answers
Answer:
7x - 2y = 39
5x + 2y = 21
Add both the equations together
12x = 60
x = 5
substitute this value for x into equation 1
35 - 2y = 39
-2y = 4
y = -2
The ordered pair (5,-2) satisfies each system.
Step-by-step explanation:
im not much of a algebra an btw
What is the answer to Which expression is equivalent to 6(3m+9).
Answers
Answer:
18
m
+
54
Step-by-step explanation:
The following set of points are on the graph of a function:
x y
2 5
3 6
4 7
5 8
6 9
7 10
Which point would be on the inverse of this function?
Group of answer choices
(-10, -7)
(-6, -3)
(-2, -5)
(9, 6)
Answers
Point (9, 6) would be on the inverse of this function so option (D) will be correct.
What is a function?A certain kind of relationship called a function binds inputs to essentially one output.
A function can be regarded as a computer, which is helpful.
The machine will only accept specified inputs, described as the function's domain, and will potentially produce one output for each input.
Given the sets of coordinates of a function.
An inverse function is the reciprocal of a function and the coordinate of the inverse function is interchanged with the original function.
For example, if (x,y) is the coordinate of the function then (y,x) will be the coordinate of the inverse of the function.
Since option (D) (9, 6) is the interchange of (6,9) so it will be the inverse of a function.
Hence "Point (9, 6) would be on the inverse of this function".
For more about the function,
brainly.com/question/23712366
#SPJ2
Find the mean, median, mode 1. 40, 38,29,34,37, 22, 15, 38 2. 26, 32, 12, 18, 11, 14, 21, 12,27 3. 3,3,4,7,5,7,6,7,8,8,8. 9,8, 10, 12, 9, 15, 15
NEED THE ANSWER ASAP
NONSENSE, REPORT
i will (brainliest) if it's correct!!!

Answers
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
Let's find the mean, median, and mode for each set of numbers:
Set: 40, 38, 29, 34, 37, 22, 15, 38
Mean: To find the mean, we sum up all the numbers and divide by the total count:
Mean = (40 + 38 + 29 + 34 + 37 + 22 + 15 + 38) / 8 = 273 / 8 = 34.125
Median: To find the median, we arrange the numbers in ascending order and find the middle value:
Arranged set: 15, 22, 29, 34, 37, 38, 38, 40
Median = (29 + 34) / 2 = 63 / 2 = 31.5
Mode: The mode is the number(s) that appear(s) most frequently in the set:
Mode = 38 (appears twice)
Set: 26, 32, 12, 18, 11, 14, 21, 12, 27
Mean: Mean = (26 + 32 + 12 + 18 + 11 + 14 + 21 + 12 + 27) / 9 = 173 / 9 ≈ 19.222
Median: Arranged set: 11, 12, 12, 14, 18, 21, 26, 27, 32
Median = 18
Mode: No mode (all numbers appear only once)
Set: 3, 3, 4, 7, 5, 7, 6, 7, 8, 8, 8, 9, 8, 10, 12, 9, 15, 15
Mean: Mean = (3 + 3 + 4 + 7 + 5 + 7 + 6 + 7 + 8 + 8 + 8 + 9 + 8 + 10 + 12 + 9 + 15 + 15) / 18 ≈ 8.611
Median: Arranged set: 3, 3, 4, 5, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10, 12, 15, 15
Median = 8
Mode: Mode = 8 (appears 4 times)
Mean: 34.125, Median: 31.5, Mode: 38
Mean: 19.222, Median: 18, No mode
Mean: 8.611, Median: 8, Mode: 8
For more questions on Mean
https://brainly.com/question/1136789
#sPJ8
What is angle S and what is angle U?

Answers
Answer:
\(m\angle S=119^\circ\), \(m\angle U=87^\circ\)
Step-by-step explanation:
Since \(STUVW \sim HIJFG\), we know that
\(m\angle S=m\angle H\) and \(m\angle U=m\angle J\)
since corresponding angles in similar triangles are equal in measure.
Therefore, looking at the second diagram, we see
\(m\angle H=119^\circ\) and \(m\angle J=87^\circ\).
Plugging these values into the equations we found in the first step, we get
\(m\angle S=m\angle H=119^\circ\) and \(m\angle U=m\angle J=87^\circ.\)
So, we have \(\boxed{m\angle S=119^\circ}\) and \(\boxed{m\angle U=87^\circ}\).
To indirectly measure the distance across a lake, Bilquis makes use of a couple
landmarks at points R and S. She measures QU, US, and TU as marked. Find the
distance across the lake (RS), rounding your answer to the nearest hundredth of a
meter.
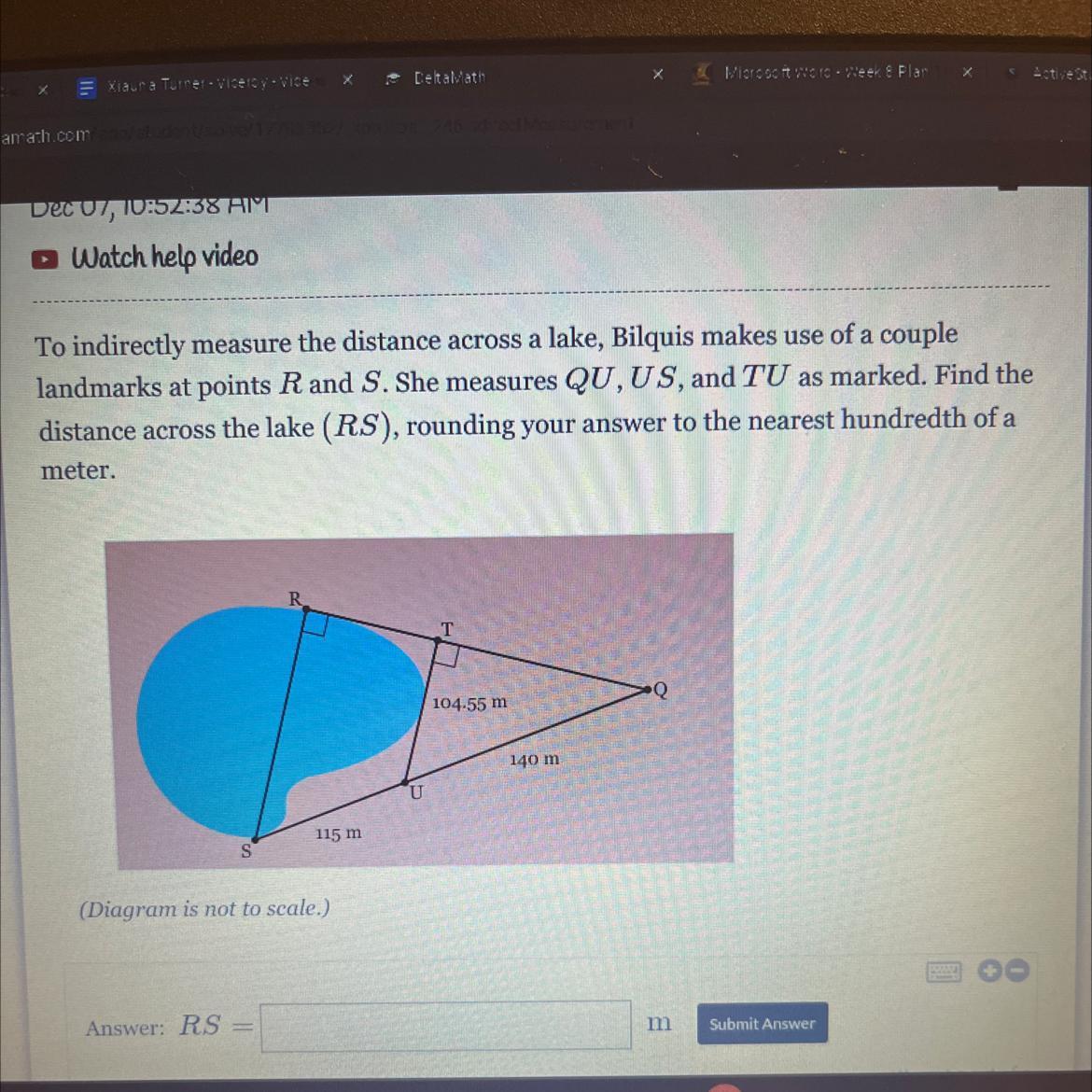
Answers
The measure of distance RS, if The sides QU = 140 m, US = 115 m, TU = 104.55 m, rounding to the nearest hundredth of a meter, is 200 m.
What is the triangle?Triangles are basic three-sided polygons with three internal angles. It is one of the basic geometric shapes, symbolized by the symbol, and has three vertex connections.
Given:
The sides QU = 140 m, US = 115 m, TU = 104.55 m
As you can see, the triangle QRS and triangle QTU are similar, thus the ratio of their sides will be equal,
QU / QS = TU / RS
140 / 140 + 115 = 104.55 / RS
140 / 255 = 104.55 \ RS
RS = 104.55 × 255 / 140
RS = 190.43 or 200 m
To know more about Triangles:
https://brainly.com/question/16886469
#SPJ1
Answer: 190.43m
Step-by-step explanation:
In Photo

answer you get brainliest and POINTS NO FILES

Answers
Answer:
hiii <33
Step-by-step explanation:
if 8 is an x intercept what is f(8)
Answers
Answer:
f(8) = 0
Step-by-step explanation:
The definition of an x intercept is a point where the function is equal to zero.
Multiply the number by 4
Add 12 to the product
Divide the sum by 2
Subtract 6 from the quotient
Answers
By comparing the result obtained in Part B (6N) with the result obtained in Part A, we can see that the conjecture holds true. The result of the process is indeed related to the original number (N) by multiplying it by 6.
Part A:
Based on the given process, the conjecture that relates the result of the process to the original number (represented as N) is as follows:
Start with the original number N.
Multiply N by 4.
Add 12 to the product.
Divide the sum by 2.
Subtract 6 from the quotient.
The result of this process is the final number obtained.
Part B:
To prove the conjecture using deductive reasoning, we will follow the steps given in Part A:
Start with the original number N.
Multiply N by 12.
Add 4 to the product.
Divide the sum by 2.
Subtract 2 from the quotient.
We will simplify the steps using algebraic notation:
Step 1: N
Step 2: 12N
Step 3: 12N + 4
Step 4: (12N + 4) / 2
Step 5: [(12N + 4) / 2] - 2
Now, let's simplify Step 5:
Step 5: (12N + 4) / 2 - 2
= (12N + 4 - 2*2) / 2
= (12N + 4 - 4) / 2
= 12N / 2
= 6N
Therefore, the result of this process is 6N.
We may verify that the supposition is correct by comparing the result from Part B (6N) with the result from Part A. By multiplying the outcome by 6, the process does in fact relate to the original number (N).
Learn more about division on:
https://brainly.com/question/25289437
The complete question is:
Multiply the number by 4. Add 12 to the product. Divide this sum by 2. Subtract 6 from the quotient. 1st number is 3 and the results 2nd number is 6 and the results 3rd number is 8 and the results 4th number is 12 and the results part A. Write a conjecture that relates the result of the process to the original number selected. Represent the original number as N. What is the result part b Represent the original number as N, use deductive reasoning to prove the conjecture in part (a) multiply the number by 12 and the results add 4 to the product and the results divide the sum by 2 subtract 2 from the quotient
Solve for x, y, and z in the system of equations.
x + 7y + 3z = 29
3z + x - 2y = −7
5y = 10 - 2x
Answers
To solve the system of equations, we can use the method of substitution or elimination. Let's use the substitution method. Simplify and solve for each variable.
Explanation:To solve the system of equations, we can use the method of substitution or elimination. Let's use the substitution method:
From the third equation, we can rewrite it as: 5y = 10 - 2x. Solving for x, we get x = 5y - 10. Now we substitute this value of x into the first equation:
(5y - 10) + 7y + 3z = 29
Simplifying, we have 12y + 3z = 39. From the second equation, we isolate z as: z = (-7 - x + 2y)/3. Now substitute the values of x and z into the equation obtained from the first equation:
12y + 3((-7 - x + 2y)/3) = 39
Simplifying further gives the following equation: 12y - 7 + 2y = 39. Combining like terms results in a quadratic equation in terms of y:
14y = 46. Solving for y, we get y = 23/7. Finally, substitute the value of y back into the previous equations to find the values of x and z.
Learn more about Solving a system of equations here:https://brainly.com/question/32115090
#SPJ1
WILL MARK BRAINLIST!!!!!
10 is 5% of what number?
What percent of 90 is 36?
4 is what percent of 20?
Answers
Answer:
1: 50
2: 2.5
3: 5
1: multiply 10 by 100 and then divide the total by 5
as follows:
(10 x 100) / 5multiply 10 by 100 and then divide the total by 5 as follows:
(10 x 100) ÷5
equals 200
2: 90 is 250% of 36
3: 4: 20*100 =
(4*100): 20 =
400: 20 = 20
6. Emily receives an inheritance of $20,000 and decides to invest the money. She puts some money in her savings
account that earns 1.5% simple interest per year. The remaining money is invested in a bond fund that returns 4.5% and a
stock fund that returns 6.2%. She makes a total of $942 at the end of 1 yr. If she invested twice as much in the bond fund
as the stock fund, determine the amount that she invested in each fund.
Answers
Emily funded $6000 in stocks and $12,000 in bond funds. She also funded the remaining $2,000 in her savings account.
Future value = $20,000
Simple interests rate = 1.5%
The return rate on bonds= 4.5%
The return rate on stocks = 6.2%
Total amount made on invests = $942
Time period = 1 year
Let us assume that the amount of money Emily invested = x
Amount invested in stock = y
If the amount is twice = 2y
The interest earned = x * 0.015
Interest on bond = 2y * 0.045
Interest on stocks = y * 0.062
The equation will be:
(x * 0.015) + (2y * 0.045) + (y * 0.062) = 942
0.015x + 0.152y = 942 ------ Equation 1
Total future value is given as $20,000
x + 2y + y = 20000
x + 3y = 20000
x = 20000 - 3y
Substituting the x value in the first equation:
0.015(20000 - 3y) + 0.152y = 942
300 - 0.045y + 0.152y = 942
0.107y = 642
y = 6000
Therefore, we can conclude that Emily funded $6000 in stocks and $12,000 in bond funds.
To learn more about the amount invested
https://brainly.com/question/31636719
#SPJ1
If $f(x) = x + 3$ and $g(x) = x^2 -6$, what is the value of $f(g(2))$?
Answers
(g.f)(−3)=7.
Explanation: Let's write down the functions. f(x)=x2−6 and g(x)=2x−1. Given we are to find what (g.f)(−3) is
The value of f(g(2)) for the condition is given by $1.
What is a function?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output. Each function has a range, codomain, and domain. The usual way to refer to a function is as f(x), where x is the input.
Given functions
f(x) = x + 3
and g(x) = x² - 6, values of each function is in $,
to determine f(g(2))
so f(g(x)) = x² - 6 + 3
f(g(x)) = x² - 3
substitute value of x
f(g(2)) = 2² - 3
f(g(2)) = 4 - 3 = $1
Hence the value of the function is $1.
Learn more about function;
https://brainly.com/question/12431044
#SPJ2
how did researchers come up with 684 coins needed to collect all of the pennies from 1959 to 1997?
Answers
The researchers came up with this number by making a model with specific coins to determine the difficulty, in terms of the probability of getting this coin.
What was the researchers purpose?The researchers Shiyoung Lu and Steven Skiena wanted to know how probable it was to collect a complete set of pennies since 1959 until 1997. By the end of this study, they decided at least 684 coins must be collected to complete this mission.
Why did they come out with this answer?Firstly, they analyze the probability for getting one coin. From this, it was concluded the probabillity was lower for old coins. After this, they used the data collected from all the coins and created an equation. This equation or model led them to conclude the answer was 684 coins.
Note: This question is incomplete because the text it refers to is missing; here is the name of the text:
"The Probabilities of Pennies"
Learn more about probability in https://brainly.com/question/11234923
#SPJ1
Which expression is equivalent to |x| > 9? Responses x < –9 and x > 9 x < –9 and x > 9 x < –9 or x > 9 x < –9 or x > 9 x > –9 and x < 9 x > –9 and x < 9 x > –9 or x < 9
Answers
\(|x| > 9\)
\(x < -9 \ \ and \ \ x > 9\)
Dora opens a savings account and puts in $ 290 at the start. Every week, she deposits $ 30 in the account. Which type of function would you use to model the relationship between the number of weeks since Dora opened the account, and the amount of money in the account
Answers
Answer:
f(x)=290+30x
Step-by-step explanation:
the 290 is for the money initially put in, the 30 is for the thirty dollars, and the x represents the number of weeks.
what is 4 over 10 plus 88 over 100
Answers
Answer:
1.28
Step-by-step explanation:
4/10 + 88/100
so this is unlike denominators so
4 times 10 and 10 times 10 equal to 40/100
so 40/100 + 88/100 equal to 128/100 so we simplify 128÷2 and 100÷2 equal to 64/50 and 64÷2 and 50÷2 equals 32/25 we do long division then it is equal to 1.28
Find the radius of each circle.

Answers
Answer:
1. 6/2 = 3
2. 10/2 = 5
simplify 2√2-3/√2+4/√8
Answers
Answer:
This is SURD, but the question is not well imputed (isn't well formed) some should be in bracket and left with one outside. check it well
A new dictionary in the shape of a rectangular prism will have a thickness of 3 33 inches ( in ) (in)left parenthesis, start text, i, n, end text, right parenthesis. The volume of the dictionary will be 216 in 3 216in 3 216, start text, i, n, end text, cubed. What must be the area of the front cover, a face perpendicular to the thickness, in square inches?
Answers
The area of the front cover a face perpendicular to the thickness is 72 in².
Given:
A new dictionary in the shape of a rectangular prism will have a thickness of 3 inches.
The volume of the dictionary will be 216in².
Volume = W×L×H
Surface = volume/ height
= 216/3
= 72 in²
Hence, the area of the front cover of a face perpendicular to the thickness is 72 in².
To learn more about the rectangular prism from the given link
brainly.com/question/25718557
#SPJ1
Give an example of two different sets of data, in which both box plots have the same range and IQR and yet represent completely different data. Explain.
Answers
Answer:
set 1 and 2
Step-by-step explanation:
Set 1 has 10
Set 2 has 13
name the quadrilateral with 2 pairs of consecutive congruent sides with diagonals that meet at a right angle
Answers
The quadrilateral you're describing is a Kite. A kite is a quadrilateral with two pairs of consecutive congruent sides, and its diagonals meet at a right angle.
Kelsey has a list of possible functions. Pick one of the g(x) functions below and then describe to Kelsey the key features of g(x), including the end behavior, y-intercept, and zeros.
g(x) = (x + 2)(x − 1)(x − 2)
g(x) = (x + 3)(x + 2)(x − 3)
g(x) = (x + 2)(x − 2)(x − 3)
g(x) = (x + 5)(x + 2)(x − 5)
g(x) = (x + 7)(x + 1)(x − 1)
Answers
The zeros of g(x) = (x + 2)(x − 1)(x − 2) are x = -2, 1 and 2
The y-intercept is g(0) = 4The end behaviour is \(\mathrm{as}\:x\to \:+\infty \:,\:g\left(x\right)\to \:+\infty \:,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:g\left(x\right)\to \:-\infty \:\)Calculating the key features of the function g(x)
From the question, we have the following parameters that can be used in our computation:
The 5 functions of g(x)
To determine the key features of the function g(x), we make use of the first
g(x) = (x + 2)(x − 1)(x − 2)
So, we have
Zeros
This is when the function equals 0
(x + 2)(x − 1)(x − 2) = 0
Evaluate
x = -2, 1 and 2
The y-intercept
This is when the value of x in the function equals 0
g(0) = (0 + 2)(0 − 1)(0 − 2)
Evaluate
g(0) = 4
End behaviour
This is the behavior of the graph of the function as it approaches the ends of the x-axis
So, we have
\(\mathrm{as}\:x\to \:+\infty \:,\:g\left(x\right)\to \:+\infty \:,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:g\left(x\right)\to \:-\infty \:\)
Read more about polynomial at
https://brainly.com/question/30833611
#SPJ1
Which box has a volume of 125 cubic feet?
4 feet
9 feet
5 feet
4 feet
3 feet
4 feet
5 feet
12 feet
2 feet
5 feet
5 feet
5 feet

Answers
Answer: Bottom left
5x5x5=125
The volume having 125 cubic, is a box which has dimensions, 5 feet, 5 feet, 5 feet. So Option D is correct
What is Volume?In mathematics, Space occupied by three dimensional objects is called Volume. Basically it is a space within a closed region of every three dimensional object.
Given that,
4 boxes having different different dimensions
1. 4 feet, 9 feet, 5 feet
2. 4 feet, 3 feet, 4 feet
3. 5 feet, 12 feet, 2 feet
4. 5 feet, 5 feet, 5 feet
lets calculate the volume for all the four boxes
V = 4 feet × 9 feet × 5 feet = 180 feet³
V = 4 feet × 3 feet × 4 feet = 48 feet³
V = 5 feet × 12 feet × 2 feet = 120 feet³
V = 5 feet × 5 feet × 5 feet = 125 feet³
Hence, the volume of box having dimension 5 feet, 5 feet, 5 feet is 125 feet³
To know more about Volume check:
https://brainly.com/question/13338592
#SPJ5
What should be subtracted from thrice the rational number -5/3 to get 1/2?
Answers
Answer:
-11/2
Step-by-step explanation:
According to the information given, you can write the following:
3(-5/3)-x=1/2, where x is the number that should be subtracted from thrice the rational number -5/3 to get 1/2.
Then, you can solve for x:
-15/3-x=1/2
-5-x=1/2
x=-5-1/2
x=-11/2
According to this, the answer is that -11/2 is what should be subtracted from thrice the rational number -5/3 to get 1/2.