Liz is watching a film in the cinema the film started at 14:30 the film is 105 minutes long when the film ends liz takes 20 minutes to get to the bus stop does she get to the bus stop in time to make it to the bus
Answers
Answer:
Step-by-step explanation:
Related Questions
If line r through (1, 1) and (5, 7) is parallel to line s through (4, -2) and (x, y), what are possible values for x and y?
Answers
If line r through (1, 1) and (5, 7) is parallel to line s through (4, -2) and (x, y),
all the possible values of x and y are those values that satisfy the equation 3x - 2y = 16.
What is a slope?In mathematics, a line's slope, also known as its gradient, is a numerical representation of the line's steepness and direction
To find the slope;
m = (y₂- y₁) / (x₂ - x₁)
Given:
If line r through (1, 1) and (5, 7) is parallel to line s through (4, -2) and (x, y),
then their slopes are equal.
(7 -1)/(5 - 1) = (y + 2)/(x-4)
3/2 = (y + 2)/(x-4)
3x - 12 = 2y + 4
3x - 2y = 16.
Therefore, all the values that satisfy the equation 3x - 2y = 16.
To learn more about the slope;
brainly.com/question/3605446
#SPJ1
which strategy would not solve the rational equation?
Answers
Answer:
This may occur when you decide to determine a function as well as a graph.
Step-by-step explanation:
Hope this helps! :D
The average value of all the pennies, nickels, dimes, and quarters in Paula's purse is 20 cents. If she had one more quarter, the average value would be 21 cents. How many dimes does she have in her purse
Answers
Answer:
Step-by-step explanation:
The average value of all the pennies, nickels, dimes, and quarters in Paula's purse is 20 cents. If she had one more quarter, the average value would be 21 cents. How many dimes does she have in her purse
help please!! i have no clue how to do this without the answer to DC

Answers
Looks like your question already has an answer! https://brainly.com/question/22200751
Find the scalar and vector projection of a onto b if a = (-1, 3, 2), b = (3, 2, -6) 1. comp ba = __
2. proj ba = __, __, __
(enter integers or fractions)
Answers
The component of b in the direction of a is `-27/7` and the vector projection of a onto b is
`(-27/49)i - (18/49)j + (54/49)k`.
Given vectors:
a = (-1, 3, 2),
b = (3, 2, -6)
We know that the scalar projection of a onto b is:
`proj(b) a = ||a|| cos θ`
And, the vector projection of a onto b is:
`proj(b) a = (a.b/ ||b||^2) b`1. comp ba (Component of b in the direction of a):
Here, we have to find the scalar projection of a onto b, `proj(b) a = ||a|| cos θ`
To find the magnitude of the vector a, we will use the magnitude formula: `||a|| = √(a1^2 + a2^2 + a3^2)`
Substitute the values of a1, a2, and a3 in the above formula. We get,`||a|| = √((-1)^2 + 3^2 + 2^2) = √14`
Now, we find the angle between the two vectors using the dot product of the two vectors: `a.b = ||a|| ||b|| cos θ`
We know that, `a.b = a1b1 + a2b2 + a3b3`
Substitute the values of a and b, we get,
`a.b = (-1)(3) + 3(2) + 2(-6) = -3 + 6 - 12 = -9`
Substitute the values of magnitudes of a and b and angle between the two vectors in the scalar projection formula: `proj(b) a = ||a|| cos θ`
We get,`proj(b) a = ||a|| (a.b/ ||a|| ||b|| cos θ)`
Putting the values, we get,
`proj(b) a = (14)(-9/ (14)(√(3^2 + 2^2 + (-6)^2) cos θ)`
On solving, we get,
`proj(b) a = -27/7`
Hence, the scalar projection of a onto b is `-27/7`.
2. proj ba (Vector projection of a onto b):
We know that the vector projection of a onto b is:
`proj(b) a = (a.b/ ||b||^2) b`
Substitute the values of a and b, we get,
`proj(b) a = ((-1)(3) + 3(2) + 2(-6))/(3^2 + 2^2 + (-6)^2) (3i + 2j - 6k)`
On solving, we get,
`proj(b) a = (-9/49) (3i + 2j - 6k)`
Hence, the vector projection of a onto b is `(-27/49)i - (18/49)j + (54/49)k`.
Thus, the component of b in the direction of a is `-27/7` and the vector projection of a onto b is
`(-27/49)i - (18/49)j + (54/49)k`.
To know more about projection visit:
https://brainly.com/question/17262812
#SPJ11
Numbers of the jerseys of 5 randamty selected Carolina Panthers Quantitative discrete Quantitative continuous. Gualitative
Answers
The numbers of the jerseys of 5 randomly selected Carolina Panthers would fall under the category of quantitative discrete data.
Quantitative data are numerical measurements or counts that can be added, subtracted, averaged, or otherwise subjected to arithmetic operations. Discrete data, on the other hand, can only take on specific, whole number values, as opposed to continuous data which can take on any value within a range.
Qualitative data, on the other hand, are non-numerical data that cannot be measured or counted numerically. Examples include colors, names, opinions, and preferences. Since the numbers of the jerseys are specific numerical values, they are considered quantitative data.
Since they can only take on specific, whole number values (i.e. the jersey numbers are not continuous values like weights or heights), they are considered discrete data. Therefore, the correct option for the given question is option "quantitative discrete".
To know more about quantitative discrete refer here:
https://brainly.com/question/32236127#
#SPJ11
the time (in minutes) between arrivals of customers to a post office is to be modelled by the exponential distribution with mean 0.75 0.75 . please give your answers to two decimal places.
Answers
The probability that the time between two arrivals is less than or equal to 1 minute is 0.42.
The time (in minutes) between arrivals of customers to a post office is to be modelled by the exponential distribution with mean 0.75.We are to calculate the probability that the time between two arrivals is less than or equal to 1 minute.We know that, for an exponential distribution, the probability density function is given by:f(x) = 1/μ e^(-x/μ)where μ is the mean of the distribution.In this case, μ = 0.75. Therefore, the probability density function is:f(x) = 1/0.75 e^(-x/0.75)To calculate the probability that the time between two arrivals is less than or equal to 1 minute, we need to integrate this probability density function from 0 to 1:f(x) = ∫0^1 1/0.75 e^(-x/0.75) dxf(x) = [-e^(-x/0.75)]0^1f(x) = -e^(-1/0.75) + e^(0)f(x) = 0.424Approximating this probability to two decimal places, we get:P(X ≤ 1) = 0.42 (rounded off to two decimal places).Therefore, the probability that the time between two arrivals is less than or equal to 1 minute is 0.42.
Learn more about probability
https://brainly.com/question/31828911
#SPJ11
What is the range of y=x^2-8x+12
Answers
Answer:
-infinity < x < infinity
Step-by-step explanation:
it has none.
Find the third, fifth, and tenth terms of the sequence described by the rule.
A(n)= -5+ (n - 1)(6)
A(3) =
(Simplify your answer.)
A(5) =
(Simplify your answer.)
A(10) =
(Simplify your answer.)

Answers
A(5)= -19
A(10)= -49
help please! hurry!! NO SPAM!!! I'll mark brainliest, if you are correct.
Which of the following represents the series in summation notation?
1 + 1/3 + 1/5 + 1/7 + 1/9 + 1/11.

Answers
Answer:
A- 1/2K-1
Step-by-step explanation:
Answer:
1/2K-1
Step-by-step explanation:

Suppose AB = AC, where B and C are nxp matrices and A is invertible. Show that B = C. Is this true, in general, when A is not invertible? What can be deduced from the assumptions that will help to show B = C? A. The determinant of A is zero. B. Since it is given that AB = AC, divide both sides by matrix A. OC. A=1 D. Since matrix A is invertible, A - 1 exists. Write an equivalent equation to AB = AC using A - 1 such that, when it is simplified, the resulting equation will simplify to B = C. What property should be used to continue simplifying the above equation? O A (AB) -1 = =B-1A-1 OB. (A-1)" = (AT) -1 C. A-1A=1 OD. (A-1)-9-A Suppose AB = AC, where B and C are nxp matrices and A is invertible. Show that B = C. Is this true, in general, when A is not invertible? O A. (AB) -1 =B-1A-1 OB. (A-1)= (AT) - 1 OC. A-1A=1 OD. (A-1)--=A Justify this next step in showing that the equation simplifies to B = C. ІВ IC B = C Is this true, in general, that AB = AC implies B = C, if A is not invertible? O A. No; it is possible that AB = AC, but B and C have different dimensions. B. 0 1 1 1 25 No; if A= B= and C= then AB = AC, yet B #C. 0 2 3 4 3 4 C. -1 Yes; one can always multiply both sides by A to cancel A. The result will always be B = C. D. Yes; the only way the products AB and AC are defined is that B and the same ensions. follows that A and must be the same matrix.
Answers
Given that AB = AC, where A is an invertible matrix, and B and C are nxp matrices, we need to show that B = C. Since A is invertible, it means that A has an inverse, denoted as A⁻¹. We can use this property to find an equivalent equation for AB = AC. Identity matrix times any matrix equals same matrix.
B = C, This proves that B = C when A is invertible. First, multiply both sides of the equation AB = AC by the inverse of matrix \(A (A⁻¹)\) on the left: \(A⁻¹(AB) = A⁻¹(AC\)). Using the associative property of matrix multiplication, we can rewrite the equation as: \((A⁻¹A)B = (A⁻¹A)C\)
Since A⁻¹A = I (the identity matrix), the equation becomes: IB = IC, Since the identity matrix times any matrix equals the same matrix, we have: B = C, This proves that B = C when A is invertible. This is because if A is singular (i.e., its determinant is zero), then it is possible for B and C to have different dimensions.
For example, if A is a 2x2 matrix with a zero determinant, then it is possible for B to be a 2x3 matrix and C to be a 2x4 matrix such that AB = AC. However, if A is not invertible, the statement AB = AC implies B = C is not always true. Consider the following counterexample:
\(A = [0, 1; 0, 2], B = [1, 1; 2, 5]\), and\(C = [1, 1; 3, 4].\) In this case, AB = AC, but B ≠ C. This demonstrates that the claim does not hold when A is not invertible.
Know more about matrix here:
https://brainly.com/question/29132693
#SPJ11
How many tiles of length and breadth 12cm and5cm will be needed to cover a rectangular region whose length and breadth are 70 cm and 36cm
Answers
Answer:
42 tiles
Step-by-step explanation:
Area of rectangular region= 70 X 36 = 2520 cm2
Area of 1 tile= 5 X 12 = 60 cm2
The number of tiles needed = Area of the rectangular region / Area of one tile = 2520/60 = 42
ayuda con esto ;v
9 6
- = -
6 X
Answers
Answer:
124 amigo dame corona no e tenido
I need this answer, ASAP please

Answers
Answer:
43
Step-by-step explanation:
2 significant figures means we keep the first 2 and round the 1 place
42.598 we round to 43 since next to the 2 is a 5 so we round up
And 43 are 2 significant figures since none of them are zero
Hopes this helps please mark brainliest
what is the population being studied warts
Answers
The average population being studied is people with warts. Specifically, this population includes individuals of all ages who have been diagnosed with any type of wart caused by a virus, such as common warts, plantar warts, and flat warts.
The population being studied is people with warts. Warts are caused by a virus and can occur anywhere on the body. Common warts, plantar warts, and flat warts are the most common types. Common warts are usually found on the hands and fingers, and are usually round and raised. Plantar warts are found on the soles of the feet and can be painful. Flat warts are usually found on the face, arms, and legs, and are generally flat and smooth. People of all ages can be affected by warts, and they are highly contagious and can be spread through contact with an infected person or surface. Treatment options include over-the-counter medicines and prescription medications, as well as cryotherapy and laser treatments. This population is being studied to better understand the causes, risk factors, and treatments for warts.
Learn more about average here
https://brainly.com/question/24057012
#SPJ4
The complete question is
what is the population being studied warts and the prevalence of warts in the population being studied?
the line tangent to the graph of g at (x y) passes through the point (-y x)
Answers
To find the equation of the tangent line, we need the slope of the line. The slope of the tangent line can be obtained by finding the derivative of the function g at the point (x, y).
The line tangent to the graph of function g at the point (x, y) passes through the point (-y, x).
Let's assume that g(x) is the given function.
The slope of the tangent line, m, is given by:
m = g'(x)
Now, let's find the equation of the tangent line using the point-slope form, where (x₁, y₁) represents the point (x, y) on the graph of g:
y - y₁ = m(x - x₁)
Substituting the values (-y, x) for (x₁, y₁), we have:
y - (-y) = m(x - x)
Simplifying, we get:
2y = m(0)
Since the slope of the tangent line is given by m = g'(x), we can rewrite the equation as:
2y = g'(x)(0)
Simplifying further, we have:
2y = 0
Dividing both sides by 2, we obtain:
y = 0
Therefore, the equation of the tangent line to the graph of g at the point (x, y) that passes through the point (-y, x) is y = 0, which is a horizontal line passing through the x-axis.
Learn more about tangent line here : brainly.com/question/31617205
#SPJ11
Which equations are equivalent to Negative one-fourth (x) + three-fourths = 12 Select all that apply. (StartFraction negative 4 x over 1 EndFraction + three-fourths = 12 Negative 1 (StartFraction x over 4 EndFraction) + three-fourths = 12 StartFraction negative x + 3 over 4 EndFraction = 12 One-fourth (x + 3) = 12 (StartFraction negative x over 4 EndFraction + three-fourths = 12
Answers
Answer:
X = -2
Explanation
12 (x+3) = 12
M e price of $2.28 per bushet, the suppy of a certain grain is 7400 mition bushels and the demand is 7500 mition bushals. At a peice of $2.37 per bushel, the topply is 7800 milion bushels and the densad is 7400 milion bushels (A) Fend a price-sopply equation of tha form p=πx+b, where p is the proe in dolars and x is the supply in mitrons of bushe't. (B) Find a crice demand equation of the form p=m+b, where p is the price in dolars and x is the demand in misions of buntiels. (C) Find the equitorum port. (D) Graph the price-supply equation, price-demand equation and oqulterim point in the same coordinale systion. (A) The price-supply equation is p or (Type an exact answer. Uso iningers or decimals for ary numbers in the oquaton)
Answers
The price-supply equation for the given scenario is p = -0.000029x + 2.5052, where p represents the price in dollars and x represents the supply in million bushels.
To find the price-supply equation, we need to determine the slope (π) and the y-intercept (b) of the equation p = πx + b. We are given two data points: at a price of $2.28 per bushel, the supply is 7400 million bushels, and at a price of $2.37 per bushel, the supply is 7800 million bushels.
Using these two points, we can calculate the slope (π):
π = (2.37 - 2.28) / (7800 - 7400) = 0.00001
Next, we can substitute one of the data points into the equation to find the y-intercept (b). Let's use the first data point (2.28, 7400):
2.28 = 0.00001 * 7400 + b
b = 2.28 - 0.074 = 2.5052
Therefore, the price-supply equation is p = -0.000029x + 2.5052, where p is the price in dollars and x is the supply in million bushels.
This equation represents the relationship between the price and supply of the grain. As the supply of the grain increases, the price decreases, indicating an inverse relationship. Similarly, as the supply decreases, the price increases. The equation allows us to estimate the price based on the given supply or vice versa.
Learn more about equation here:
https://brainly.com/question/10724260
#SPJ11
Please help me solve
Answers
Answer:
I could but can you please put down the problem.
Step-by-step explanation:
let d be the solid region bounded by the paraboloids and . write six different triple iterated integrals for the volume of d. evaluate one of the integrals.
Answers
To find the volume of the solid region bounded by the paraboloids y = x^2 and z = 4 - x^2, we need to set up triple iterated integrals in terms of x, y, and z.
One way to do this is to integrate over x first, then y, then z, or vice versa. Here are six different triple iterated integrals we can use:
1. ∫∫∫d dz dy dx
2. ∫∫∫d dx dy dz
3. ∫∫∫d dx dz dy
4. ∫∫∫d dy dx dz
5. ∫∫∫d dy dz dx
6. ∫∫∫d dz dx dy
Let's evaluate the first integral:
∫∫∫d dz dy dx
We start by finding the limits of integration for z. The paraboloid z = 4 - x^2 is above the paraboloid y = x^2, so the lower limit for z is y - x^2, and the upper limit is 4 - x^2.
Next, we find the limits of integration for y. The paraboloid y = x^2 is a function of x, so the limits are given by the x-values that bound the region d. Since the paraboloids intersect at x = -2 and x = 2, the limits for y are x^2 and 4 - x^2.
Finally, we find the limits of integration for x. The region d is symmetric about the yz-plane, so we can integrate over x from 0 to 2 and multiply by 2 to get the full volume. Therefore, the limits for x are 0 and 2.
Putting it all together, we have:
∫∫∫d dz dy dx = ∫0^2 ∫x^2^(4-x^2) ∫y-x^2^(4-x^2) dz dy dx
Evaluating this integral is a bit messy, but it can be done with some algebraic manipulation and trigonometric substitutions. The answer turns out to be: 64/15
Visit here to learn more about paraboloids brainly.com/question/30925041
#SPJ11
Which expression represents the situation below?
Fourteen less than the product of seven and ten.
(My younger sister needs help, so if u could, thanks!)
Answers
Answer:
=14-(7*10)
Step-by-step explanation:
fourteen = 14 (base)
less = -
PRODUCT means multiplication
PRODUCT of seven and ten = 7*10
*Don't forget parenthesis
Answer= 14 - (7*10)
A rock is tossed from a platform and follows a parabolic path through the air. The height of the rock in metres is given by h(t) = -5t² + 12t + 14 where t is measured in seconds. a) How high is the rock off the ground when it is thrown? b) How long is the rock in the air? c) For what times is the height of the rock greater than 17 metres? d) How long is the rock above the height of 17 metres?
Answers
Given information:h(t) = -5t² + 12t + 14 where t is measured in seconds.a) How high is the rock off the ground when it is thrown?For h(0), the initial height of the rock is required.h(0) = -5(0)² + 12(0) + 14 = 14 meters.
For h(t), the rock's maximum height needs to be found to determine the time when the rock hits the ground. In order to determine the maximum height, first, we need to find the time of maximum height using the formula:
tmax = -b/2a = -12/2(-5) = 1.2s
Now, h(1.2) can be found to determine the maximum height:
h(1.2) = -5(1.2)² + 12(1.2) + 14 = 20.8 meters
Therefore, the rock is in the air for (1.2*2) 2.4 seconds.c) For what times is the height of the rock greater than 17 metres?This means h(t) > 17. Solving this inequality gives:-
5t² + 12t + 14 > 17
=> -5t² + 12t - 3 > 0
=> (-5t + 3)(t - 1) > 0
From part c, we know that the rock's height is greater than 17 metres between 0 and 0.6 seconds and after 1 second. Therefore, the time the rock is above 17 metres is the sum of these two time periods:0.6 seconds + (2 - 1) seconds = 1.6 seconds.
To know more about inequality visit:-
https://brainly.com/question/28823603
#SPJ11
Let X be a random variable that is the sum of two dice when they are thrown. What is the probability density function (PDF) of X?
Answers
Answer:
This is the probability density function of X.
Step-by-step explanation:
To find the PDF of X, we need to find the probability of each possible value of X.
When two dice are thrown, the possible outcomes are the integers from 2 to 12, with each outcome having an equal probability of 1/36. Therefore, the PDF of X can be represented as follows:
P(X = 2) = 1/36
P(X = 3) = 2/36
P(X = 4) = 3/36
P(X = 5) = 4/36
P(X = 6) = 5/36
P(X = 7) = 6/36
P(X = 8) = 5/36
P(X = 9) = 4/36
P(X = 10) = 3/36
P(X = 11) = 2/36
P(X = 12) = 1/36
This is the probability density function of X.
To know more about probability density, refer here:
https://brainly.com/question/29129585
#SPJ11
PUT 80 POINTS ON THIS!!! DUE TODAY HELP! Community Gym charges a $60 membership fee and a $65 monthly fee. Workout Gym charges a $200 membership fee and a $55 monthly fee. After how many months will the total amount of money paid to both gyms be the same? What will the amount be?
Answers
Answer:
The amount will be y = 970
Step-by-step explanation:
Equation 1:
y = 60 + 65x
Equation 2:
y = 200 + 55x
Solve for x and y
60 + 65x = 200 + 55x
10x = 140
x = 14
y = 200 + 55 (14)
y = 970
HOPE THIS HELPS :)
Answer:
1) 14 months
2) $970
Step-by-step explanation:
We know that the Community Gym charges a $60 membership fee and a $65 monthly fee.
So, we can write the following equation:
\(y=60+65m\)
Where y is the total cost, 60 is the one-time membership fee, and 65m is the cost for m months.
Workout Gym charges a $200 membership fee and a $55 monthly fee. So, we can write the following equation:
\(y=200+55m\)
Where y is the total cost, 200 is the one-time membership fee, and 55m is the cost for m months.
Question 1)
We want to know after how many months will the total amount of money paid to both gyms be the same. So, let's set the equations equal to each other:
\(60+65m=200+55m\)
To find the number of months, let's solve for m.
Subtract 55m from both sides:
\(60+10m=200\)
Subtract 60 from both sides:
\(10m=140\)
Divide both sides by 10:
\(m=14\)
So, after 14 months, the cost of going to Community Gym or Workout Gym will be the same.
Question 2)
To find the amount, simply substitute 14 back into either equation. Let's do it for both.
We have:
\(y=60+65m\)
Substitute 14 for m:
\(y=60+65(14)\)
Multiply and add:
\(y=60+910=\$970\)
We have:
\(y=200+55m\)
Substitute 14 for m:
\(y=200+55(14)\)
Multiply and add:
\(y=200+770=\$970\)
So, after 14 months, both gym will cost $970.
And we're done!
Try It
Given: AD
Prove: DE
D
BC and BCD =
CE
Hint
B
Angles Segments Triangles Statements Reasons
AAS
CPCTC
Statements
✓ 1. AD = BC
✓2. ZBCD =
3. DC DC
4. AADC = ABCD
5. LEDC ZECD
SAS
converse of isosceles triangle thm
Reasons
1. given
2. given
3. reflexive property
4. SAS
5. CPCTC

Answers
The required statements and reasons to prove that DE is equal to CE is explained.
What is a triangle congruence theorem?The triangle congruence theorem is a theorem that can be used to prove that two or more triangles are the same, considering the corresponding properties of the triangles. The properties are length of the sides, and measure of internal angles.
The statements and reasons to prove that DE is equal to CE are explained below using the triangle congruence theorem.
STATEMENT REASON
1. AD = BC Given
2. <BCD = <ADC Given
3. DC = DC Reflexive property
4. ΔADC ≅ ΔBCD SAS
5. <EDC ≅ <ECD CPCTC
6. AC = BD Definition of diagonal
7. DE = CE Congruent sides of isosceles triangle
Learn more about the triangle congruence theorem at https://brainly.com/question/18922904
#SPJ1
Evaluate 11.5x + 10.9y when x = 6 and y =7
Answers
The value of the algebraic expression 11.5x + 10.9y at x = 6 and y = 7 is 145.3
What is an algebraic expression?
Algebraic expression consists of variables and numbers connected with addition, subtraction, multiplication and division
The given algebraic expression is 11.5x + 10.9y
We have to find the value of the algebraic expression at x = 6 and y = 7
Putting x = 6 and y = 7 in the algebraic expression,
\(11.5 \times 6 + 10.9 \times 7\)
69 + 76.3
145.3
To learn more about algebraic expression, refer to the link-
https://brainly.com/question/2164351
#SPJ1
help me please need help
missing lengths

Answers
Step-by-step explanation:
For example ............

Answer:
4. y=3√2 and x=36
Step-by-step explanation:
Here,
interior angle of triangle = 180°
So, 90°+45°+45°=180°
Therefore, the triangle is isosceles triangle
So,
y=3√2 (the corresponding sides of corresponding angle of isosceles triangle are equal)
Again, x^2=(3√2)^2 + (3√2)^2
or, x= √(18 + 18)
or, x=√36
or, x=6
need help asap !!!!!
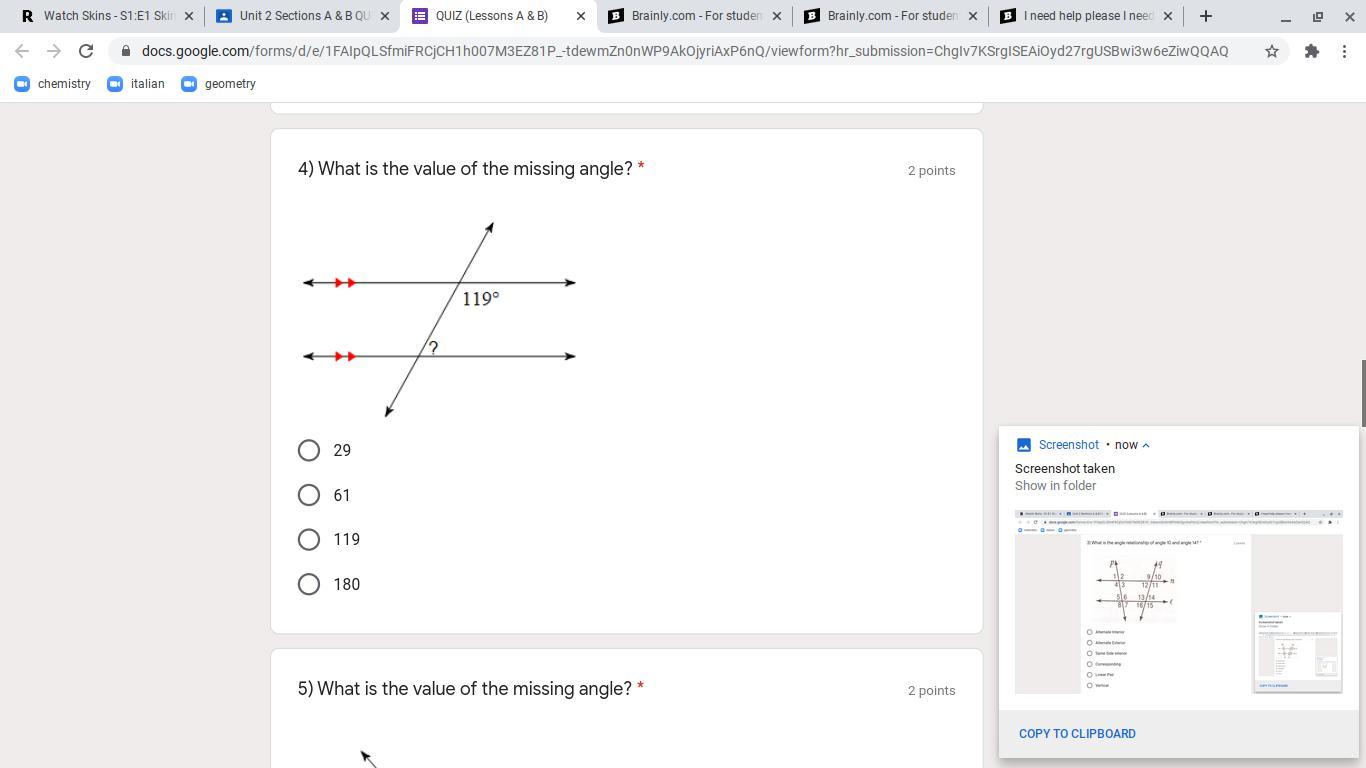
Answers
Answer:
61
Step-by-step explanation:
the angle of 119 degrees is equal to the angle on the angle on the exterior of the question mark. So all you gotta do is subtract 180-119
There is a line through the origin that divides the region bounded by the parabola y=5x−3x^2 and the x-axis into two regions with equal area. What is the slope of that line?
Answers
The slope of the line that divides the region bounded by the parabola \(y=5x-3x^2\)and the x-axis into two regions with equal area is 5.
To find the slope of the line that divides the region into two equal areas, we need to determine the point of intersection between the parabola and the x-axis. Since the line passes through the origin, its equation will be y = mx, where m represents the slope.
Setting the equation of the parabola equal to zero, we find the x-values where the parabola intersects the x-axis. By solving the equation\(5x - 3x^2 = 0\), we get x = 0 and x = 5/3.
To divide the region into two equal areas, the line must pass through the midpoint between these x-values, which is x = 5/6. Plugging this value into the equation of the line, we have y = (5/6)m.
Since the areas on both sides of the line need to be equal, we can set up an equation using definite integrals. By integrating the equation of the parabola from 0 to 5/6 and setting it equal to the integral of the line from 0 to 5/6, we can solve for m. After performing the integration, we find that m = 5.
Therefore, the slope of the line that divides the region into two equal areas is 5.
Learn more about: Parabola
brainly.com/question/11911877
#SPJ11
A(-2,3)
Triangle ABC has vertices at A(-2,3), B(-3,6), and
C(2,-1) Is triangle ABC a night triangle? If so, which
angle is the night angle?
O No, the triangle has no right angles.
O Yes, the right angle is angle A
O Yes, the right angle is angle B
O Yes, the right angle is angle C
VA
C (2-1)
B (-3,-6)

Answers
second choice i’m prolly wrong