Answers
Continuous Compound
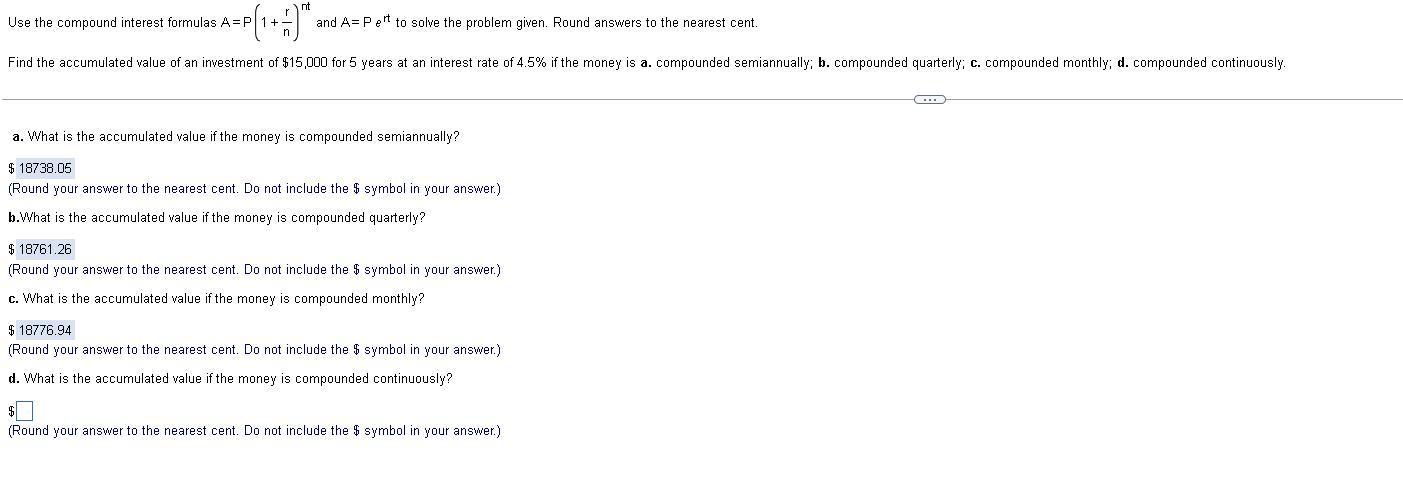
An initial investment of P dollars at an interest annual rate r will have a final value A given by:
\(A=P\cdot e^{r\cdot t}\)The investment is P = $15,000 at a rate of r = 4.5% = 0.045. The accumulated (or final) value for t = 5 years is:
\(\begin{gathered} A=15,000\cdot e^{0.045\cdot5} \\ \text{Calculating:} \\ A=15,000\cdot e^{0.225} \\ A=15,000\cdot1.252323 \\ A=18,784.84 \end{gathered}\)The Accumulated value is $18,784.84
Related Questions
what is the minimum value of 18.60
Answers
Answer:
The minimum value is 18.55 and the maximum value is 18.64. When rounding to one decimal place, you must look at the number two places after the decimal. If this is bigger than 5 round up and lower than 4 round down.
Step-by-step explanation:
Jamar is going to invest $2200 and leave it in an account for 14 years. Assuming the interest is compounded continuously what interest rate to the nearest hundredths of a percent would be required in order for Jamar to end up with $4200
Answers
Assuming the interest is compounded continuously what interest rate to the nearest hundredths of a percent would be required in order for Jamar to end up with $4200 is 4.62%.
How is the interest rate for continuous compounding determined?Using the formula r = ln(A/P) / t, the interest rate, r, can be determined using an online finance calculator as follows:
Total P+I (A) = $4,200.00
Principal (P) = $2,200.00
Compound (n) = Compounding Continuously
Time (t in years) = 14 years
R = 4.619% per year
The calculation steps are as follows:
Solving for rate r as a decimal
r = ln(A/P) / t
r = ln(4,200.00/2,200.00) / 14
r = 0.0461877
Then convert r to R as a percentage:
R = r * 100
R = 0.0461877 * 100
R = 4.62%/year
Thus, the interest rate required to get a total amount of $4,200.00 from compound interest on a principal of $2,200.00 compounded continuously over 14 years is 4.62% per year.
Learn more about continuous compounding at https://brainly.com/question/14303868.
#SPJ1
Points are (-5,1) (-4,2) (-1,3)
I need it in y=
Please be fast!!

Answers
Answer:
(5,1) (4,2) (1,3)
Step-by-step explanation:
since is going a clockwise rotation the -x(5,4,1) all will become positive
After a shopping trip to the mall. Ashley saw $6.10 in her purse she spent 525 80 on a pair of shoes, 59.25 on a necklace, and $18.85 on a belt. How much money did Ashley bring to the mall
Answers
9514 1404 393
Answer:
$60
Step-by-step explanation:
The total she started with is the sum of the amount she spent and the amount remaining:
$25.80 +$9.25 +$18.85 +$6.10 = $60.00
Ashley brought $60.00 to the mall.
Answer:
The Total money she bring to mall is $ 60.
Step-by-step explanation:
Given that :-
After a shopping trip to the mall. Ashley saw $6.10 in her purse she spent $ 25.80 on a pair of shoes, 59.25 on a necklace, and $18.85 on a belt.
To find :-
How much money did Ashley bring to the mall ?
Solution :-
Total money she bring to the mall = sum of amount she spend and amount remaining.
Total money = $ 25.80 + $ 59.25 + $ 18.85 + $6.10
Hence, The total money she bring to mall is $ 60.00.
i need help can someone help me right now!!!!!!

Answers
(a) | BD | bisects | AC | (reason : Given)
(b) |AD| ≅ |CD| (reason: |BD| is the perpendicular bisector of segment AC).
(c) ∠ABD ≅ ∠CBD (reason: | BD | bisects angle ABC)
(d) ∠A ≅ ∠ C (reason: complementary angles of a right triangle)
What is the complete proof of the congruent angles?Congruent angles are the angles that have equal measure. So all the angles that have equal measure will be called congruent angles.
From the first statement, we will complete the flow chart as follows;
line BD bisects line AC (reason : Given)
line AD is congruent to line CD (reason: line BD is the perpendicular bisector of segment AC)
Angle ABD is congruent to angle CBD (reason: line BD bisects angle ABC)
Angle A is congruent to angle C (reason: angle ABD = angle CBD, and both triangles ABD and CBD are right triangles).
Learn more about congruent angles here: https://brainly.com/question/28262429
#SPJ1
22)A company ships computer components in boxes that contain 50 items. Assume that theprobability of a defective computer component is 0.2. Find the probability that the firstdefect is found in the seventh component tested. Round your answer to four decimalplaces.
Answers
Answer:
ok so they test 7 components so the probity of getting a bad one for each is 0.2 so we just multiply this 7 times
0.2*0.2*0.2*0.2*0.2*0.2*0.2=0.0000128
Hope This Helps!!!
The required probability will be 0.0000128 that the first defect is found in the seventh component tested.
What is probability?Probability is defined as the possibility of an event being equal to the ratio of the number of favorable outcomes and the total number of outcomes.
We have been given that a company ships computer components in boxes that contain 50 items.
Assume that the probability of a defective computer component is 0.2.
As per the given condition, the required solution would be as:
They test seven components, and the probability of obtaining a defective one for each is 0.2, so we just multiply this by seven.
⇒ 0.2×0.2×0.2×0.2×0.2×0.2×0.2
⇒ 0.0000128
Thus, the required probability will be 0.0000128 that the first defect is found in the seventh component tested.
Learn more about probability here:
brainly.com/question/11234923
#SPJ5
Wei wants to prove that the segment joining midpoints of two sides of a
triangle is parallel to the third side.
Select the appropriate rephrased statement for Wei's proof.

Answers
Now we know PR∥QX , according to construction with transversal line TX.
∠PTS=∠QXS (Alternate angle)
In △PTS and △QSX
∠PTS=∠QXS (Alternate angle)
∠PST=∠QSX(vertically opposite angles)
PS=SQ(S is mid point of PQ)
△PTS≅△QSX(AAS rule)
So, TP=QX(CPCT)
As we know, TP=TR (T is midpoint)
Hence, TR=QX
Now, in quadrilateral TSQR
TS∥QR
Hence proved.
Know more about triangle,
https://brainly.com/question/13677972
#SPJ1
In a Survey at a local university 69% of students so that they get less than the recommended eight hours of sleep per night. In a group of 4800 students how many would you expect to get eight or more hours of sleep per night
Answers
A 2 meter television camera at ground level is filming the lift-off of a space shuttle at a point 750 meters from the launch pad. The camera’s angle of elevation to the shuttle is 32° at this specific time . Find the height of the shuttle.
Answers
To find the height of the shuttle, we can use trigonometry and the concept of similar triangles. The height of the shuttle is approximately 468.675 meters.
Let's assume that the height of the shuttle is represented by 'h' meters. From the information given, we know that the distance between the camera and the launch pad is 750 meters, and the angle of elevation from the camera to the shuttle is 32 degrees.
Using trigonometry, we can set up the following equation:
tan(32°) = h / 750
To find the value of h, we can rearrange the equation:
h = tan(32°) * 750
Using a calculator, we can find the value of tan(32°) ≈ 0.6249.
Now we can calculate the height of the shuttle:
h ≈ 0.6249 * 750
h ≈ 468.675 meters
Therefore, the height of the shuttle is approximately 468.675 meters.
For more such questions on trigonometry
https://brainly.com/question/24349828
#SPJ8
6. (09.04 LC)
For the equation y = 6x2 – 9x + 22, choose the correct application of the quadratic formula. (5 points)
X
-6+1(6)- 4(-9)(22)
2(-9)
X
6 + (6)- 4-9)(22)
21-9)
--9 +1(-99) - 4(6)(22)
X
2(6)
X
9+(-9) - 4(6)(22)
2(6)
Answers
Given:
The quadratic equation is
\(y=6x^2-9x+22\)
To find:
The correct application of the quadratic formula.
Solution:
If a quadratic equation is \(ax^2+bx+c=0\), then the quadratic formula is
\(x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
We have,
\(y=6x^2-9x+22\)
Putting \(y=0\), we get
\(6x^2-9x+22=0\)
Here, \(a=6,b=-9,c=22\). Using the quadratic formula, we get
\(x=\dfrac{-(-9)\pm \sqrt{(-9)^2-4(6)(22)}}{2(6)}\)
The correct application of the quadratic formula is \(x=\dfrac{-(-9)\pm \sqrt{(-9)^2-4(6)(22)}}{2(6)}\).
Note: The options are not in proper format.
the average commute time for a random sample of students who commute to campus at ksu is 23.4 minutes. the 95% confidence interval to estimate the mean commute time for the population of ksu students is (15.2, 31.6). which of the following is the best interpretation for this information?
Answers
We are 95% confident that the true population, mean commute time for the commuter students at KSU is between 15.2 and 31.6 minutes.
We are 95% certain that the true population mean falls within this interval based on the 95% confidence interval. Therefore, if it applies to the student population and not the sample, it is not about the population's distribution. This confidence interval is an inference about the population, not the sample. Therefore, we cannot claim that 95% of the population resides inside those two miles. All that matters is how confident we are that the population parameter falls within that range.
To know more about the true population visit: brainly.com/question/15872322
#SPJ4
Jamal is five years less than the age of his brother Alex and the product of their ages is 300. How old is Jamal?
Answers
Let's start by defining some variables:
Let's call Jamal's age "J".
Let's call Alex's age "A".
From the problem statement, we know that:
J = A - 5 (Jamal is 5 years younger than Alex)
J * A = 300 (the product of their ages is 300)
We can use the first equation to substitute J in the second equation:
(A - 5) * A = 300
Expanding the left-hand side:
A^2 - 5A = 300
Moving all terms to the left-hand side:
A^2 - 5A - 300 = 0
We can solve for A using the quadratic formula:
A = (-(-5) ± sqrt((-5)^2 - 41(-300))) / (2*1)
A = (5 ± sqrt(25 + 1200)) / 2
A = (5 ± sqrt(1225)) / 2
Since A is a positive integer, we take the positive solution:
A = (5 + 35) / 2 = 20
Now we can use the first equation to find J:
J = A - 5 = 20 - 5 = 15
Therefore, Jamal is 15 years old.
100 pts..\(ANSWER this question for your God's sake PLZ..\)
![100 pts..[tex]ANSWER this question for your God's sake PLZ..[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/4K4WftcsRMQyPboKYgkaGGzFzlNbM2yJ.jpeg)
Answers
Answer:
Step-by-step explanation:
a) \(5y+ab\)
b) \(f^{3} -3\\\)
c) \(6kq\)
d) \(\frac{3xy}{2w} \\\\\)
e) \(3x-4\sqrt{z} \\\)
f) \(\frac{2p}{5q} \\\\\)
\(a) 5y+ab5y+ab
b) \begin{gathered}f^{3} -3\\\end{gathered}
f
3
−3
c) 6kq6kq
d) \begin{gathered}\frac{3xy}{2w} \\\\\end{gathered}
2w
3xy
e) \begin{gathered}3x-4\sqrt{z} \\\end{gathered}
3x−4
z
f) \begin{gathered}\frac{2p}{5q} \\\\\end{gathered}
5q
2p
\)
14 is what percent of 350?
Answers
Answer:
4%
Step-by-step explanation:
Unit 6 similar triangles homework 5 page 2
Answers
Using the proportional side rule for similar triangles, all the values of x can be found as below.
What are Similar Triangles?Similar triangles are triangles which has the same shape but different size.
The length of sides are proportional in similar triangles.
1) Side lengths of bigger triangle are 32 + x and 24 + 9 = 33.
Corresponding proportional sides of smaller triangles are 32 and 24 respectively.
Using proportion,
\(\frac{32+x}{32}\) = \(\frac{33}{24}\)
Cross multiplying,
(32 + x) 24 = 32 × 33
768 + 24x = 1056
4x = 288
x = 12
2) Side lengths of bigger triangle are 33 + x and 20 + 14= 34.
Corresponding proportional sides of smaller triangles are x and 14 respectively.
\(\frac{33+x}{x}\) = \(\frac{34}{14}\)
462 + 14x = 34x
20x = 462
x = 23.1
3) Side lengths of bigger triangle are 30 + x + 5 = 35 + x and 36.
Corresponding proportional sides of smaller triangle are 30 and 20 respectively.
\(\frac{35+x}{30}\) = \(\frac{36}{20}\)
700 + 20x = 1080
20x = 380
x = 19
4) Side lengths of bigger triangle are x + 8 + 2x - 5 = 3x + 3 and 20 + 22.5 = 42.5.
Corresponding proportional sides of smaller triangles are 2x - 5 and 22.5 respectively.
\(\frac{3x+3}{2x-5}\) = \(\frac{42.5}{22.5}\)
67.5x + 67.5 = 85x - 212.5
17.5x = 280
x = 16
5) Side lengths of bigger triangle are 2x+4 +4 = 2x + 8 and x+7+3 = x + 10.
Corresponding proportional sides of smaller triangles are 2x + 4 and x + 7 respectively.
\(\frac{2x+8}{2x+4}\) = \(\frac{x+10}{x+7}\)
(2x + 8) (x + 7) = (x + 10) (2x + 4)
2x² + 8x + 14x + 56 = 2x² + 20x + 4x + 40
22x + 56 = 24x + 40
2x = 16
x = 8
6) Side lengths of bigger triangle are 2x + 8 + 5x - 4 = 7x + 4 and 82.
Corresponding proportional sides of smaller triangles are 2x + 8 and 28 respectively.
\(\frac{7x+4}{2x+8}\) = \(\frac{82}{28}\)
196x + 112 = 164x + 656
32x = 544
x = 17
Hence the values of x in each of the triangles are found.
Learn more about Similar Triangles here :
https://brainly.com/question/8019077
#SPJ1

The graph shows a proportional relationship between the distance a car travels and the fuel it consumes.
Distance (miles)
280
240
200
160
120
.80
40
0
1
2
3
4
Fuel (gallons)
Based on the graph, the car requires
5 6
gallons of fuel to travel 100 miles.

Answers
Based on the graph the car requires 2.5 gallons of fuel to travel 100 miles.
Given:
The graph shows a proportional relationship between the distance a car travels and the fuel it consumes.
Distance (miles) Fuel(gallons)
0 0
40 1
80 2
120 3
160 4
200 5
240 6
280 7
From the table:
1 gallon fuel = 40 miles
1 mile = 1/40 gallon fuel
multiply by 100 on both sides
100 miles = 100/40 gallons fuel
100 miles = 5/2 gallons fuel
100 miles = 2.5 gallons fuel.
Therefore the car requires 2.5 gallons of fuel to travel 100 miles.
Learn more the distance and fuel here:
https://brainly.com/question/28809733
#SPJ1
Find the value of y if the line through the points (3, y) and (2, 5) has slope m = -8.
y =
Answers
y-2= -8(x-5)
Step-by-step explanation:
thats the right answer trust me
Suppose that you borrow $13,000 for 5 years at 7% toward the purchase of a car.
The monthly payment is $
The total interest for the loan is $
Answers
The total interest for the loan is $4,550. This means that over the course of 5 years, you will pay back the original loan amount of $13,000 plus $4,550 in interest for a total of $17,550.
To calculate the total interest for this loan, we need to use the simple interest formula:
Monthly EMI formula :
Interest = Principal x Rate x Time
In this case, the principal (amount borrowed) is $13,000, the rate is 7%, and the time is 5 years.
So,
Interest = $13,000 x 0.07 x 5
Interest = $4,550
It's important to keep in mind that this calculation assumes that the interest rate remains constant over the entire 5-year period.
To learn more about : interest
https://brainly.com/question/25720319
#SPJ8
PLEASE HELP HURRY
The camp director is ready to purchase the cable. Use the distance between the trees and the change in height of the cable to determine the length of cable needed. Be sure to include:
• the required 5% slack in the line, and
• 6 extra feet of cable at each end to wrap around each tree.
Enter the total length, in feet, of cable needed.
slope constraint: the slope of the zip line should be 6 to 8 feet of vertical change for every 100 feet of horizontal change
Answers
To calculate the length of cable needed, we first need to determine the length of the zip line itself. We can use the distance between the trees and the change in height of the cable to calculate the horizontal and vertical distances.
Let's say the distance between the trees is 200 feet and the change in height is 80 feet. To ensure a 6 to 8 feet of vertical change for every 100 feet of horizontal change, we need to limit the horizontal distance to between 750 and 1000 feet.
We can use the Pythagorean theorem to calculate the length of the zip line:
horizontal distance = √(100^2 - 80^2) = 60 feet
total length of zip line = √(200^2 + 60^2) = 208.44 feet
To account for the required 5% slack in the line, we need to add 5% to the total length:
total length with slack = 208.44 + (0.05 * 208.44) = 218.86 feet
To wrap around each tree, we need an additional 6 feet at each end, so we need to add 12 feet to the total length:
total length with slack and extra cable = 218.86 + 12 = 230.86 feet
Therefore, we need a total length of 230.86 feet of cable.
Step-by-step explanation:
To determine the length of cable needed for the zip line, we first need to calculate the horizontal distance between the two trees. Let's assume that the distance between the trees is d feet. We also need to calculate the vertical change in height of the cable between the two trees. Let's assume that the height difference is h feet.
Given the slope constraint, we know that for every 6 to 8 feet of vertical change, we need 100 feet of horizontal change. This means that the slope of the zip line should be between 6/100 and 8/100. We can use this information to set up a proportion:
vertical change / horizontal change = slope
h / d = 6/100 or h / d = 8/100
Solving for d in each of these equations, we get:
d = h / (6/100) = 100h / 6 = 50h / 3 (for the minimum slope of 6/100)
d = h / (8/100) = 100h / 8 = 25h / 2 (for the maximum slope of 8/100)
To account for the required 5% slack in the line, we need to increase the length of the cable by 5%. This means that the actual length of cable needed is:
L = 1.05d + 12
where 12 feet represents the 6 extra feet of cable needed at each end to wrap around each tree.
Substituting the expressions for d that we derived earlier, we get:
L = 1.05(50h/3) + 12 = (175h/6) + 12 (for the minimum slope of 6/100)
L = 1.05(25h/2) + 12 = (131h/40) + 12 (for the maximum slope of 8/100)
Therefore, the total length of cable needed for the zip line depends on the height difference between the trees and the desired slope of the line. For example, if the height difference is h = 50 feet and we want to use the minimum slope of 6/100, then the total length of cable needed would be:
L = (175(50)/6) + 12 = 1462.5 feet
If we want to use the maximum slope of 8/100, then the total length of cable needed would be:
L = (131(50)/40) + 12 = 73.2 + 12 = 85.2 feet
Note that these values are approximations and do not take into account factors such as the weight of the rider or the tension of the cable.
I need help figuring out the answers for this

Answers
Interest, is an additional money paid for borrowing money. it could be simple or compound interest.
simple interest= p×T×R/100
when interest is compounded annually
F= p(1+r)^t
F= future value
p= principal
r= rate
t= time
compound interest is calculated based on the initial and accumulated interest.
interest Linda earnsfist yearF= p(n+r)^n
F= 10000(1+0.02)^1
F= 10000×1.02= $10200
interest= 10200-10000
interest = $200
second year
F = 10200(1+0.02)^1
F=10200×1.02= $10404
Interest= 10404-10200
interest= $204
third year
F= 10404(1+0.02)^1
F= 10404(1.02)
F = $10612.08
interest= 10612.08-10404
interest= $208.08
Bob's interestI= p×t×R/100first year
I=10000×1×0.02/100
interest= $2
second year
I= 10000×2×0.02/100
interest= $4
for the third year
I =10000×3 × 0.02/100
interest= $6
check answer above for final computation
Bridget Riley was just one of many artists associated with the 1960's 'Op Art' Movement. True or false
Answers
Answer:
True
Explanation:
Bridget Riley was one of the most prominent artists associated with the 1960s 'Op Art' movement, which was an art movement that explored optical illusions and effects to create abstract art that played with the viewer's perception. However, there were many other artists associated with this movement, including Victor Vasarely, Richard Anuszkiewicz, and Yaacov Agam, among others.
Suppose 50 rabbits are on Groff Farm… DOUBLING every year…
How many rabbits after 5 years?
How many rabbits after 10 years?
Answers
Answer:
Step-by-step explanation:
After the first year, the number of rabbits will double from 50 to 100.
After the second year, the number of rabbits will double again from 100 to 200.
This doubling process will continue for a total of 5 years, so after 5 years, the number of rabbits will be:
Number of rabbits after 5 years = 50 x 2^5 = 50 x 32 = 1600
Therefore, there will be 1600 rabbits on Groff Farm after 5 years.
Similarly, after 10 years, the number of rabbits will double 10 times:
Number of rabbits after 10 years = 50 x 2^10 = 50 x 1024 = 51200
Therefore, there will be 51,200 rabbits on Groff Farm after 10 years.
Express as a product. 1+2cos a
Answers
Answer:
Therefore, 1 + 2cos a can be expressed as the product of 2 and (cos a/2 + 1).
1 + 2cos a = 2(cos a/2 + 1)
Step-by-step explanation:
We can use the trigonometric identity:
cos 2a = 1 - 2 sin^2 a
to rewrite 1 + 2cos a as:
1 + 2cos a = 1 + 2(1 - sin^2 a/2)
= 1 + 2 - 2(sin^2 a/2)
= 3 - 2(sin^2 a/2)
Now, using another trigonometric identity:
sin a = 2 sin(a/2) cos(a/2)
we can rewrite sin^2 a/2 as:
sin^2 a/2 = (1 - cos a)/2
Substituting this into the expression for 1 + 2cos a, we get:
1 + 2cos a = 3 - 2((1 - cos a)/2)
= 3 - (1 - cos a)
= 2 + cos a
Therefore, 1 + 2cos a can be expressed as the product of 2 and (cos a/2 + 1).
1 + 2cos a = 2(cos a/2 + 1)
if 3*2=12,3*5=24and 15-6=3then 16/2=?
a.4
b.6
c.8
d.12
Answers
Answer:
16 divided by 2 equals C which is 8.
Step-by-step explanation:
Hans has two route options to drive to work. When he travels Hampton Road, the distribution of times is approximately Normal with a mean of 23.9 minutes and a standard deviation of 3.1 minutes. When Hans travels Route 8, the distribution of times is approximately Normal with a mean of 20.8 minutes and a standard deviation of 5.4 minutes. Hans randomly selects 11 times he drove Hampton Road and 11 different times that he drove Route 8. What is the probability the mean time of the Hampton Road trips will be less than the mean of the Route 8 trips?
Answers
Answer: 0.0493 Chance of Probability
The parent absolute value function is reflected across the x-axis and translated right 2 units. Which function is represented by the graph?
–|x – 2|
–|x + 2|
|–x| – 2
|–x| + 2
Answers
The function represented by the graph with the given transformations is |–x| + 2.
The function represented by the given transformations is |–x| + 2.
Let's analyze the transformations step by step:
Reflection across the x-axis:
Reflecting the parent absolute value function across the x-axis changes the sign of the function. The positive slopes become negative, and the negative slopes become positive. This transformation is denoted by a negative sign in front of the function.
Translation right 2 units:
Translating the function right 2 units shifts the entire graph horizontally to the right. This transformation is denoted by subtracting the value being translated from the input of the function.
Combining these transformations, the function |–x| + 2 results. The negative sign reflects the function across the x-axis, and the subtraction of 2 units translates it right. The absolute value is applied to the negated x, ensuring that the function always returns a positive value.
Thus, the function represented by the graph with the given transformations is |–x| + 2.
For more questions on function
https://brainly.com/question/30905449
#SPJ8
Answer: -lx-2l
Step-by-step explanation:
dawgs i need the answer

Answers
Answer:
3rd option.
Step-by-step explanation:
figure u dont need one
Write the number name and expanded form for 710,231
Answers
Answer:
seven hundred ten and two hundred and thirty one 700,000+ 10,000+ 200+30+1
Step-by-step explanation:
Which of the following statements are true regarding functions?
Check all that apply.
Answers
Answer:
The horizontal line test may be used to determine whether a function is one-to-one.
The vertical line test may be used to determine whether a relation is a function.
Step-by-step explanation:
BOOMER GENERATION: At 84%, Boomers are the highest amongst all the generations that want to shop in-store. In a sample size of 75 people in the Boomer Generation, estimate how many of them prefer to shop in-store.
Answers
In a sample size of 75 people in the Boomer Generation, proportionately, the estimated number of people who prefer to shop in-store is 63.
What is proportion?Proportion shows the relative number of objects or people in the whole.
Proportions are ratios equated to each other.
They are expressed as fractional values, in decimals, percentages, and fractions.
The percentage of Boomers who want to shop in-store = 84%
The sample size of the Boomer Generation = 75
The estimated number of Boomers in the sample size who want to shop in-store = 63 (75 x 84%)
Thus, 63 Boomers representing 84 percent of 75 want to shop in-store.
Learn more about proportions and percentages at https://brainly.com/question/9184010
#SPJ1