Martha found a rectangular box wrapped in beautiful Christmas wrapping under
the Christmas Tree. The present was 20 cm high and twice as long as it was wide.
If it had a surface area of 1600 cm?, what was the volume of the present?

The number of days it will take the crew to lay all the track is; 27 days

The number of miles of track the crew has left to lay after 18 days is; 65 miles

We are given the equation that represents the length L (in miles) that is left to lay after d days as;

L(d) = 189 - 7d

where;

L is length in miles

d is number of days

Thus, the number of days it will take to lay all the tracks is;

Number of days = 189/7

Number of days = 27 days

The length L (in miles) that is left to lay after 18 days is;

L= 189 - 7(18)

L= 189 - 126

L= 65 miles

Read more about Algebraic Equations at; https://brainly.com/question/16269951

#SPJ1

Complete question is;

A railroad crew can lay 7 miles of track each day. They need to lay 189 miles of track. The length, L (in miles), that is left to lay after d days is given by the following function. L(d) = 189 - 7d​

(How many days will it take the crew to lay all the track?)

(How many miles of track does the crew have left to lay after 18 days?)

Answer: cos4

Step-by-step explanation: 50 meters

B. 50-√3 meters

C. 100 meters

D. 100-√3 meters

40. What expression is used to answer: "A 4-m tall man stands on horizontal ground 43 m from a tree.

The angle of depression from the top of the tree to his eyes is 22°. Estimate the height of the tree."

A. sin 22

B. cos 22

C. tan 22

D. cot 22

Answer:

Below

Step-by-step explanation:

You didn't say the SHAPE of the object (cube? Pyramid?)

assuming it is a cube, there will be six equal sides of 4x4

6   x 4x4 = 96 cm^2

Answer:

Yes

Step-by-step explanation:

Pythagorean's Theorum is that a^2 + b^2 = c^2

a and b are the sides of the triangle and c is the hypotenuse. 33x33+56x56=4225 sqrt4225 is 65. Everything checks out.

Answer:

Step-by-step explanation:

$100x0.5x1=$5

Answer:

100

Step-by-step explanation:

60*2=120

10 seats taken up on 2 buses=20

120-20=100

Answer:

the last one (100) 60+60 equals120 10+ 10 equals 20 120-20 equals 100

The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).

To solve this problem, we can use the concepts of trigonometry and related rates.

Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.

Given:

The plane is flying with a constant speed of 360 km/h.

The plane passes over the radar station at an altitude of 1 km.

The plane is climbing at an angle of 30°.

We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.

We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:

sin(30°) = 1/D.

To find dD/dt, we can differentiate both sides of this equation with respect to time:

cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.

Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:

cos(30°) * 0 = -1/D^2 * dD/dt.

We can substitute the known values:

cos(30°) = √3/2,

D = 1 km.

Therefore, we have:

√3/2 * 0 = -1/(1^2) * dD/dt.

Simplifying further:

0 = -1 * dD/dt.

This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.

for such more question on distance

https://brainly.com/question/7243416

#SPJ8

The variance and standard deviation of the highest temperatures recorded in eight specific states are 108.89 and 10.435 respectively.

The given data is 112, 100, 127, 120, 134, 118, 105, and 110.

We need to find the variance and standard deviation of the highest temperatures recorded in eight specific states.

Variance and Standard Deviation are the two important measurements in statistics. Variance is a measure of how data points vary from the mean, whereas standard deviation is the measure of the distribution of statistical data.

We know that, variance \(=\frac{(x_{i}-x )}{n}\) , Where x is mean and n is the number of observations.

Now, the average of given numbers \(=\frac{112+100+127+120+134+118+105+110}{8} =115.75\)

Variance\(=\frac{(-3.75)^{2} +(-15.75)^{2}+(11.5)^{2}+(4.25)^{2}+(18.25)^{2}+(2.25)^{2}+(-10.75)^{2}+(2.25)^{2}}{8}\)

\(=\frac{14.0625+248.0625+132.25+18.0625+333.0625+5.0625+115.5625+5.0625}{8}= \frac{871.1875}{8}=108.89\)

We know that, standard deviation \(=\sqrt{Variance} =\sqrt{108.89} =10.435\).

Therefore, the variance and standard deviation of the highest temperatures recorded in eight specific states are 108.89 and 10.435 respectively.

To learn more about variance and standard deviation visit:

https://brainly.com/question/17084031.

#SPJ1

Answer and Step-by-step explanation:

To find out how many more yards of red fabric Reuben used, we need to subtract the amount of yellow fabric from the amount of red fabric. Since the two fractions have different denominators, we need to find a common denominator before subtracting them. The least common multiple of 8 and 4 is 8, so we can rewrite both fractions with a denominator of 8:

7/8 - 1/4 = 7/8 - (1/4) * (2/2) = 7/8 - 2/8 = (7 - 2)/8 = 5/8

So, Reuben used 5/8 yards more red fabric than yellow fabric.

Answer:

Translate 3 right and 1 up.

Step-by-step explanation:

Looking at the picture and count the movement.

Answer:

Step-by-step explanation:

3 units right.

1 unit up.

Each of the letters is moved by these amounts to create the new image.

A sequence of transformations that maps △ABC to △A′B′C′ is a rotation of 90° counterclockwise about the origin followed by a translation 2 units right.

Transformations are changes done in the shapes on a coordinate plane by rotation, reflection, or translation

https://brainly.com/question/4289712

A sequence of transformations that maps △DEF to △D′E′F′ is a rotation of 90° counterclockwise about the origin followed by a translation two units right.

The sequence of vertices ABC(DEF in this question) is clockwise, as is the sequence of A'B'C'(D'E'F in this question). Thus, an even number of reflections is involved, if any reflections are involved. The offered choices do not include suitable reflections.

The orientation of AB(DE) is toward the right. The orientation of A'B'(D'E') is up, so there must be a rotation of 90° CCW. Rotation of 90° CCW about the origin will leave the figure in a position that is 2 units left of where it is shown. The rotation must be followed by a translation 2 units to the right.

Thus, we conclude that a sequence of transformations that maps △DEF to △D′E′F′ is a rotation of 90° counterclockwise about the origin followed by a translation two units right.

Read more about Sequence of Transformations at; https://brainly.com/question/4289712

#SPJ1

The value of side EA is,

EA = 16.9

We have to given that;

Circle E with diameter CD and radius EA.

And, AB is tangent to E at A.

Here, AB = 34 and EB = 38

Hence, By using Pythagoras theorem we get;

AB² + AE² = EB²

34² + AE² = 38²

1156 + AE² = 1444

AE² = 1444 - 1156

AE² = 288

AE = √288

AE = 16.9

Thus, The value of side EA is,

EA = 16.9

Learn more about the circle visit:

https://brainly.com/question/24810873

#SPJ1

Answer:

{x,y}={  5/9,0}

Step-by-step explanation:

9x - 2y = 5

y = 0

9x - 2•() = 5

9x = 5

x = 5/9

By now we know this much :

   x = 5/9

   y = 0

⇒{x,y} = {5/9,0}

Answer:

Please check the explanation.

Step-by-step explanation:

Given the equation

\(9x + 2y = 5\)

solving the equation for y

\(9x + 2y = 5\)

Step 1: Add -9x to both sides

\(9x+2y+-9x=5+-9x\)

\(2y=-9x+5\)

Step 2: Divide both sides by 2

\(\frac{2y}{2}=\:\frac{-9x+5}{2}\)

\(y=\frac{-9}{2}x+\frac{5}{2}\)

Thus, the value of y is:

\(y=\frac{-9}{2}x+\frac{5}{2}\)

If we put y = 0 in the \(9x + 2y = 5\)

\(9x+\left(0\right)=5\)

\(9x=5\)

\(\mathrm{Divide\:both\:sides\:by\:}9\)

\(\frac{9x}{9}=\frac{5}{9}\)

\(x=\frac{5}{9}\)

Thus, the value of x=5/9 at y=0

Answer:

10

Step-by-step explanation:

If f is F-measurable and non-negative on E ∈ F and µ(E) = 0

thenREf dµ = 0.ProofLet 0 ≤ s ≤ f be a simple, F-measurable function. So s =PNn=1 anχAnfor some an ≥ 0,

An ∈ F. Then IE(s) = PNn=1 anµ(An ∩ E). But µ ismonotone which means that µ(An ∩ E) ≤ µ(E) = 0 for all n and so IE(s) =0 for all such simple functions.

Hence I(f, E) = {0} and so REf dµ =sup I(f, E) = 0. ¥Lemma 4.7 If g ≥ 0 and REgdµ = 0 thenµ{x ∈ E : g(x) > 0} = 0.Proof Let A = {x ∈ E : g(x) > 0} and An = {x ∈ E : g(x) >1n}.

Thenthe sets An = E ∩ {x : g(x) >1n} ∈ F satisfy A1 ⊆ A2 ⊆ A3 ⊆ ... withA =S∞n=1 An. By lemma 4.1 µ(A) = limn→∞ µ(An). Usingsn(x) = ½ 1nif x ∈ An0 otherwise,so sn ≤ g on An we have1nµ(An) = IAn(sn)≤RAngdµ by the definition of RAn≤REgdµ

Thereom 4.4(iii)= 0 by assumption.So µ(An) = 0 for all n and hence µ(A) = 0. ¥Definition If a property P holds on all points in E \ A for some set A withµ(A) = 0 we say that P holds almost everywhere (µ) on E, written as a.e.(µ)on E.

(*It might be that P holds on some of the points of A or that the set ofpoints on which P does not hold is non-measurable.

This is immaterial. Butif µ is a complete measure, such as the Lebesgue-Steiltje’s measure µF, thenthe situation is simpler.

Assume that a property P holds a.e.(µ) on E.

Thedefinition says that the set of points, D say, on which P does not hold can becovered by a set of measure zero, i.e. there exists A : D ⊆ A and µ(A) = 0.

Yet if µ is complete then D will be measurable of measure zero.In this section we are not assuming that µ is complete.)

Answer:

Graph is below.

Step-by-step explanation:

The solutions of the equations are : x = [8 ± √ 40] / 4

Given,

Y=2x² - 8x+3

Now,

To get the solution of equation equate it to 0 .

2x² - 8x+3  = 0

By quadratic formula,

x = -b ± √ b² - 4ac/2a

Substitute the values in the formula,

x = [8 ± √ 64 - 4(2)(3)] / 2* 2

x = [8 ± √ 40] / 4

Now plot the points in the graph. The graph is attached below.

Know more about equations,

https://brainly.com/question/17181370

#SPJ6

The total number of wickets after the final match was 22.

Since Paras Khadka takes 5 wickets for 26 run in the final match due to which his bowling average improves by 2, and his old bowling average was 14, to determine what is the total number of wickets after the final match the following calculation must be performed:

Therefore, the total number of wickets after the final match was 22.

Learn more about maths in https://brainly.com/question/23830341

For each pound of the blend, Cold Beans should use 3 pounds of Guatemalan coffee.

This means that in a 6-pound bag of the blend, they would use \(3 \times 6 = 18\)pounds of Guatemalan coffee.

Let's assume that x pounds of Guatemalan coffee are used per pound of the blend.

Given information:

Cost of Guatemalan coffee = $11/lb

Cost of the other coffee = $5/lb

Desired cost of the blend = $8/lb

Total weight of the blend = 6 pounds

To find the ratio of Guatemalan coffee to the total blend, we can set up the equation:

\((x \times 11 + (6 - x) \times 5) / 6 = 8\)

In this equation, \((x \times 11)\) represents the cost of the Guatemalan coffee in the blend, and\(((6 - x) \times 5)\) represents the cost of the other coffee in the blend.

The numerator is the total cost of the blend, and we divide it by 6 (the total weight of the blend) to find the cost per pound.

Now, let's solve the equation for x:

(11x + 30 - 5x) / 6 = 8

6x + 30 = 48

6x = 48 - 30

6x = 18

x = 18/6

x = 3

Therefore, for each pound of the blend, Cold Beans should use 3 pounds of Guatemalan coffee.

This means that in a 6-pound bag of the blend, they would use \(3 \times 6 = 18\)pounds of Guatemalan coffee.

To summarize, to achieve a cost of $8 per pound for a 6-pound bag of blend, Cold Beans should use 3 pounds of Guatemalan coffee per pound of the blend.

For similar question on cost.

https://brainly.com/question/2292799  

#SPJ8

The total distance of the obstacle course can be calculated by finding the distance between each pair of consecutive points and adding them up. The distance between two points (x1, y1) and (x2, y2) can be calculated using the formula: distance = sqrt((x2 - x1)^2 + (y2 - y1)^2).

Using this formula, we can calculate the distances between each pair of consecutive points as follows:

Start to Tire Race: distance = sqrt((-40 - (-40))^2 + (-30 - (-10))^2) = 20 yards

Tire Race to Rope Climb: distance = sqrt((40 - (-40))^2 + (-30 - (-30))^2) = 80 yards

Rope Climb to Monkey Bars: distance = sqrt((40 - 40)^2 + (20 - (-30))^2) = 50 yards

Monkey Bars to Finish: distance = sqrt((10 - 40)^2 + (20 - 20)^2) = 30 yards

Adding up all these distances, we get a total distance of 20 + 80 + 50 + 30 = 180 yards for the obstacle course.

Answer:

\(\huge\boxed{\sf 187.5\ gal.}\)

Step-by-step explanation:

Given that:

For,

12 ft. height, gas tank can hold 450 gal.

Using unitary method:

12 ft = 450 gal.

Divide 12 to both sides

1 ft = 450/12 gal.

1 ft = 37.5 gal.

Multiply 5 to both sides

5 ft. = 37.5 × 5 gal.

5 ft. = 187.5 gal.

So, the height of 5 ft. holds 187.5 gal.

\(\rule[225]{225}{2}\)

Answer:

187.5 gal

Step-by-step explanation:

A=lw

450=12(w)

450/12=37.5ft

A=lw

A=37.5(5)

A=187.5 gal

Hope that helps

Answer:

\((-27)^\dfrac{2}{3}\) = 9

Step-by-step explanation:

Given that,

Asn expression : \((-27)^\dfrac{2}{3}\)

We need to evaluate the above expression.

We know that, \((-3)^3=-27\)

So,

\((-27)^\dfrac{2}{3}=(-3)^{3\times \dfrac{2}{3}}\)

or

\(=(-3)^2\\\\=-3\times -3\\\\=9\)

So, the value of \((-27)^\dfrac{2}{3}\) is 9. Hence, the correct option is (b).

The equivalent equation of  r sinθ = 10 in rectangular coordinates is y²  +   y⁴/x² - 100 = 0.

The rectangular coordinates is calculated from the polar equation as follows;

r sinθ = 10

the conversion from polar to rectangular coordinates;

r² = x² + y²

r = √(x² + y²) ----- (1)

y/x = tanθ  ------ (2)

r sinθ = 10

√(x² + y²)(y/x) = 10

(x² + y²)(y²/x²) = 100

y²  +   y⁴/x² = 100

y²  +   y⁴/x² - 100 = 0

Learn more about rectangular coordinates here: https://brainly.com/question/1402079

#SPJ1

Answer:

nah

Step-by-step explanation:

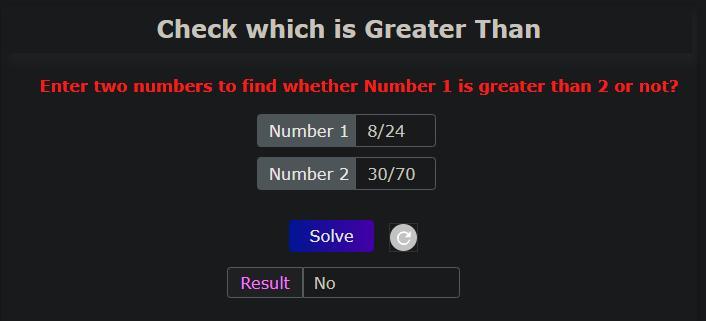
Answer:

8/24<30/70

Step-by-step explanation:

8/24=1/3=.33

30/70=3/7=.428571

8/24<30/70

The statement that is true regarding the function f(x) = (x-4)(x + 1) is that the function is increasing for all real values of x where x < -1 and where x > 4. So, the option is: O The function is increasing for all real values of x where x < -1 and where x > 4.

Explanation: Given function is:f(x) = (x - 4) (x + 1). The graph of the given function is shown below: As it is visible from the graph, the function is decreasing for all real values of x where x lies between -1 and 4 (inclusive).

The turning point of the function is x = -0.5, which is the x-coordinate of the vertex of the parabola. Also, we see that the vertex is the minimum point of the parabola and the y-coordinate of the vertex is -4.25. This means that f(x) ≥ -4.25 for all x. The function is increasing for all real values of x where x < -1 and where x > 4.

For more questions on: function

https://brainly.com/question/29631554

#SPJ8        

There is no stationary point at x = 2. The nature of the curve at x = 2 cannot be determined since there is no stationary point.

To verify that the curve has a stationary point at x = 2, we need to find the derivative of the equation and set it equal to zero.

Given the equation:

y = 2x + 1/(x-1)²

Let's find the derivative dy/dx:

dy/dx = d/dx [2x + 1/(x-1)²]

To find the derivative, we can use the power rule and the chain rule. Let's differentiate each term separately:

For the first term, 2x, the derivative is 2.

For the second term, 1/(x-1)², we can rewrite it as (x-1)^(-2) to apply the power rule. The derivative is then:

d/dx [(x-1)^(-2)] = -2(x-1)^(-3) * d/dx (x-1)

Using the chain rule, d/dx (x-1) = 1, so the derivative becomes:

-2(x-1)^(-3) * 1 = -2/(x-1)^3

Now, let's set dy/dx equal to zero and solve for x:

-2/(x-1)^3 = 0

This equation is satisfied when the numerator is equal to zero:

-2 = 0

However, -2 is not equal to zero, which means there is no x value that makes dy/dx equal to zero.

For more question on stationary point click on

https://brainly.com/question/28978328

#SPJ11

The general solution of the partial differential equation is:

U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)

The partial differential equation (PDE) is given as:

Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)

Assume that the solution can be written as a product of two functions:

U(x, t) = X(x)T(t)

Substituting this into the PDE, we have:

X''(x)T(t) = (1/2)X(x)T'(t)

Dividing both sides by X(x)T(t), we get:

(X''(x))/X(x) = (1/2)(T'(t))/T(t)

Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:

(X''(x))/X(x) = -λ²

(1/2)(T'(t))/T(t) = -λ²

Simplifying the second equation, we have:

T'(t)/T(t) = -2λ²

Solving the second equation, we find:

T(t) = Ce^(-2λ²t)

Applying the boundary condition U(0, t) = 0, we have:

U(0, t) = X(0)T(t) = 0

Since T(t) ≠ 0, we must have X(0) = 0.

Applying the boundary condition U(3, t) = 0, we have:

U(3, t) = X(3)T(t) = 0

Again, since T(t) ≠ 0, we must have X(3) = 0.

Therefore, we can conclude that X(x) must satisfy the following boundary value problem:

X''(x)/X(x) = -λ²

X(0) = 0

X(3) = 0

The general solution to this ordinary differential equation is given by:

X(x) = Asin(λx) + Bcos(λx)

Applying the initial condition U(x, 0) = 5*sin(4πx), we have:

U(x, 0) = X(x)T(0) = X(x)C

Comparing this with the given initial condition, we can conclude that T(0) = C = 5.

Therefore, the complete solution for U(x, t) is given by:

U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)

where:

Σ represents the summation over all values of n

λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).

To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):

X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0

X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0

From the first equation, we have Bₙ = 0.

From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.

This implies that 3λₙ = nπ, where n is an integer.

Therefore, λₙ = (nπ)/3.

Substituting the eigenvalues into the general solution, we have:

U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)

where Aₙ are the coefficients that can be determined from the initial condition.

Read more about Partial Differential Equations at: https://brainly.com/question/28099315

#SPJ1

The statement that applies to the sample math is:

B. the work shown to remove all fractions is not correct

The given steps are:

y = ¹/₄x + 2

- I first isolate the constant.

- After doing so, I get the equation: -¹/₄x + y = 2

- To remove the fraction, I multiply by –4, giving the equation x - 4y=2, which is the final answer.

The correct steps are as follows:

y = ¹/₄x + 2

First isolate the constant to get: y - ¹/₄x = 2

To remove the fraction, Multiply the obtained equation by –4

So, Equation : x - 4y = -8

On comparing both the work we can see that in the given work the removal of fraction is done incorrectly

They didn't multiply -4 on the right hand side .

Thus, option B applies.

Read more on subject of formula at: https://brainly.com/question/657646

#SPJ1

Answer:

(x-x)/(y-y)

Step-by-step explanation:

Slope is defined by the change in y divided by the change in x, not the change in x divided by the change in y.

Answer:

A - Yes, it's a solution

Answer:

Yes, it is a solution.

Step-by-step explanation:

The reason why it is a solution because when you plug -3 into the y and add -3+6<4, you will get -9<4. -9 is less than 4 because the 9 is a negative. Hope this helps!