Mason had 30 dollars to spend on 3 gifts. He spent 10 1/4
dollars on gift A and 3 4/5
dollars on gift B. How much money did he have left for gift C?
Answers
Mason had 15.95 dollars left to spend on gift C.
To calculate how much money Mason had left for gift C, we need to subtract the amounts spent on gifts A and B from the total amount he had initially.
Mason had $30 to spend on 3 gifts. He spent $10 1/4 on gift A, which can be expressed as 10.25 dollars, and $3 4/5 on gift B, which can be expressed as 3.8 dollars.
Now we can calculate the amount of money Mason had left for gift C:
Amount spent on gifts A and B = 10.25 + 3.8 = 14.05 dollars
To find the amount left for gift C, we subtract the amount spent from the total amount:
Amount left for gift C = Total amount - Amount spent on gifts A and B
Amount left for gift C = 30 - 14.05 = 15.95 dollars
Therefore, Mason had 15.95 dollars left to spend on gift C.
For more questions on spend visit:
https://brainly.com/question/31635142
#SPJ8
Related Questions
Neil is growing sugar crystals for his science fair experiment. He wants to find out if the amount of sugar affects the size of the crystal. Neil adds 18 tablespoons of sugar to his first bowl of water. He plans to add less sugar to the second bowl
Answers
Neil is growing sugar crystals for his science fair experiment. He wants to find out if the amount of sugar affects the size of the crystal. Neil adds 18 tablespoons of sugar to his first bowl of water. He plans to add less sugar to the second bowl.
The purpose of Neil's experiment is to find out if the amount of sugar affects the size of the crystal. Neil adds 18 tablespoons of sugar to his first bowl of water and plans to add less sugar to the second bowl. Sugar crystals form by cooling a hot, concentrated sugar solution. After the crystals have grown, Neil should weigh and measure their size. Neil will then compare the sizes of the crystals from each bowl. If he concludes that adding more sugar to the water causes the crystals to grow larger, Neil's hypothesis will have been supported. The independent variable is the amount of sugar, which is the amount Neil adds to each bowl of water. The dependent variable is the size of the sugar crystals.For such more questions on Neil
https://brainly.com/question/31278726
#SPJ8
Find the values of x and y. Write your answers in simplest form.

Answers
Answer:
y=7
Step-by-step explanation:
x=3
What is the equation of the line that passes through the point (-3, 4) and has a
slope of 1
Answers
Solve the proportion20/3 = ?/6
Answers
Let the unkown be x. the given proportion would be
20/3 = x/6
By crossmultiplying, it becomes
x * 3 = 20 * 6
3x = 120
x = 120/3
x = 40
The correct option is C
part 3, Q 3
Rotating EF¯¯¯¯¯¯¯¯90∘
clockwise would produce the same image as rotating CD¯¯¯¯¯¯¯¯
_____∘
clockwise.
Enter your answer as the whole number that correctly fills in the blank.

Answers
Rotating EF 90° clockwise would produce the same image as rotating CD
270° counterclockwise
What is the transformation rule?There are different ways of transformations such as:
Rotation
Dilation
Translation
Reflection
Now, the coordinates are given as:
EF = E(4, -5) and F(3, -2)
Now, rotation by 90° clockwise would produce:
E'(-5, -4) and F(-2, -3)
This is a rotation rule of (x, y) → (y, -x)
Thus, if CD has the coordinates C(-4, 5) and D(-3, 2), then the rotation by 270° counterclockwise would produce:
C'(5, 4) and D(2, 3)
Read more about Transformation rule at: https://brainly.com/question/29200683
#SPJ1
I need help on homework.

Answers
J = (3,0)
K = (3,negative two)
L = [ 0, negative two]
I apologise for the way this is set out, half of the keys on my laptop do not work
Answer:
J- (3,0)
K- (3,-2)
L- (1,-2)
Reasoning- Just move the points to where it's asking.
Joseph and Raquel are building a scale model of the Alamo Mission for their Texas history project using a scale in which 2 inches represents 30 feet. The enclosed area of the Alamo Mission was 480 feet long and 160 wide.
What should the length of the enclosed area of the scale model be in inches?
Answers
Th length of the enclosed area of the scale model in inches is 32 inches.
How to find the length of the enclosed area of the scale model in inches?Joseph and Raquel are building a scale model of the Alamo Mission for their Texas history project using a scale in which 2 inches represents 30 feet.
The enclosed area of the Alamo Mission was 480 feet long and 160 feet wide.
The length of the enclosed area of the scale model in inches can be calculated as follows:
30 feet = 2 inches
480 feet = ?
cross multiply
length of the enclosed area = 480 × 2 / 30
length of the enclosed area = 960 / 30
length of the enclosed area = 32 inches
learn more on scale model here:https://brainly.com/question/22377661
#SPJ1
A solid oblique pyramid has a regular hexagonal base with an area of 54StartRoot 3 EndRoot cm2 and an edge length of 6 cm. Angle BAC measures 60°. A solid oblique pyramid has a regular hexagonal base with an area of 54 StartRoot 3 EndRoot centimeters squared and an edge length of 6 centimeters. Point B is the apex and point A is the center of the hexagon. Point C is a corner of the hexagon. Triangle A B C is formed. Angle A is 60 degrees and angle C is 90 degrees. What is the volume of the pyramid? 72StartRoot 3 EndRoot cm3 108StartRoot 3 EndRoot cm3 324 cm3 486 cm3
Answers
Answer: C. 324 cm∧3
Just took quiz.
Based on the calculations, the volume of this pyramid is equal to: D. 324 cm³.
Given the following data:
Base area = 54√3 cm².Edge length = 6 centimeters.Angle BAC = 60°.How to calculate the volume of a pyramid?Mathematically, the volume of a pyramid can be calculated by using this formula:
Volume = 1/3 × base area × height
Next, we would find the height of this pyramid from the right-angled triangle ABC by applying Tan trigonometry formula:
Tanθ = Opp/Adj = BC/AC
Tan60 = height/6
√3 = height/6
Height = 6√3 cm.
Now, we can calculate the volume of this pyramid:
Volume = 1/3 × base area × height
Volume = 1/3 × 54√3 × 6√3
Volume = 1/3 × 972
Volume = 324 cm³.
Read more on pyramid here: brainly.com/question/16315790
#SPJ2

I need help please help me :C

Answers
Part 1:
To find the distance between two points, we can use the distance formula:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
Substituting the values into the formula, we get:
d = sqrt((7 - 3)^2 + (3 - 6)^2)
Simplifying, we get:
d = sqrt(4^2 + (-3)^2)
d = sqrt(16 + 9)
d = sqrt(25)
d = 5
Therefore, the distance between the points (3, 6) and (7, 3) is 5 units.
PART 2:
d = sqrt(64 + 36)
d = sqrt(100)
d = 10
Therefore, the distance between the points (1, 7) and (9, 1) is 10 units.
#SPJ1
If \text{m}\overset{\Large\frown}{DR} = 34^{\circ}m DR ⌢ =34 ∘ and \text{m}\overset{\Large\frown}{SV} = 94^{\circ}m SV ⌢ =94 ∘ , find \text{m}\angle Lm∠L
Answers
The measures of the corresponding inscribed angles, and then add those angles together to find the measure of angle L. Therefore, the measure of angle L is 64 degrees.
The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. In other words, if we have an angle whose vertex is on the circumference of a circle, and whose sides intersect two points on the circumference, then the measure of the angle is half the measure of the arc between those two points.
In this problem, we are given the measures of two arcs, DR and SV, and we want to find the measure of angle L. We can start by using the Inscribed Angle Theorem to find the measures of the corresponding inscribed angles. Let's call these angles A and B, where A is the inscribed angle that intercepts arc DR, and B is the inscribed angle that intercepts arc SV.
Using the Inscribed Angle Theorem, we can find that m∠A=12m⌢DR=12(34∘)=17∘m∠B=12m⌢SV=12(94∘)=47∘
To find the measure of angle L, we simply add angles A and B together: m∠L=m∠A+m∠B=17∘+47∘=64∘
Therefore, the measure of angle L is 64 degrees.
Learn more about Measures:
brainly.com/question/2384956
#SPJ11
A survey of 2400 was given to people who owned a certain type of car, 960 said they would buy that type of car again. What percent of the people surveyed were completely satisfied with the car.
Answers
Divide the number satisfied by total people surveyed then multiply by 100 for the percent.
960/2400 = 0.4
0.4 x 100 = 40%
The answer is 40%
A researcher interviews 6 widows about their marriages and notices how many cats are wandering around. Is there a significant relationship between the number of times an old widow was married and the number of cats the old lady owns? ( You don't need to do the math to calculate it - the Pearson r is given).
Times Married: 1 1 2 2 3 3
Cats Owned: 3 2 4 5 5 6
Pearson r = +.91
Write up the conclusion for this study in APA format and be sure to include the r2.
Answers
There is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Given, the Pearson correlation coefficient of +0.91,
There appears to be a strong +ve correlation between the number of cats she owns and the number of times an old widow was married.
It suggests that the more times a widow was married,the more cats she tends to own.
Approximately 82% of the variance in the number of cats owned can be explained by the number of times a widow was married is indicated by the coefficient of determination (r²).
Hence, we can say that there is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Learn more about Pearson correlation coefficient here,
https://brainly.com/question/31801929
#SPJ4
What is the product of (2i) and (5+3i)?
Group of answer choices
-6 + 10i
10 + 6i
16i
10 - 6i
Answers
-6 + 10i
Step-by-step explanation:
Greetings !
Write the expression in product form
\(2i \times (5 + 3i)\)
Apply distributive law a(b+c)=ab+ac
\(2i5 + 2i3i\)
Multiply the numbers
2.5=10=10iMultiply the numbers
2.3=6Apply exponent rule aa=a²
\(ii = i {}^{2} \\ = 6i {}^{2} \)
Apply imaginary number rule i²=-1
=6(-1)=-6
\( = 10i - 6\)
Rewrite in standard complex form:
\( - 6 + 10i\)
Hope it helps!
I need help with this right now
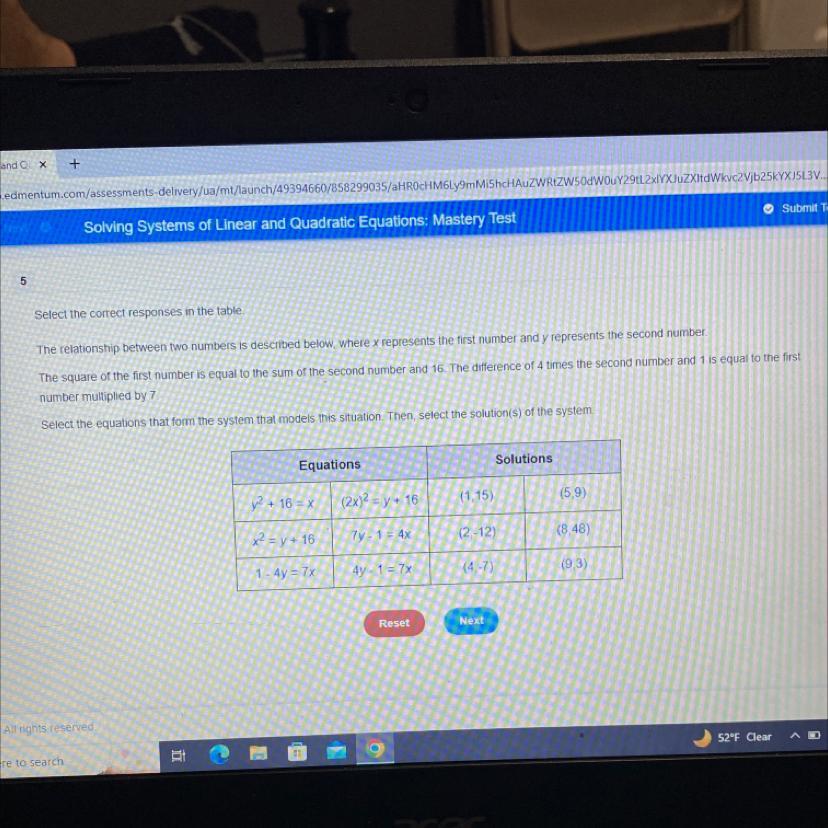
Answers
The equations are x² = y + 16 & 4y - 1 = 7x and the solution is (5, 9)
Selecting the numbers and the solutionsFrom the question, we have the following parameters that can be used in our computation:
x = first number
y = second number
Given that
The square of the first number is 16 more than the second number
This means that
x² = y + 16
Also, we have the difference expression to be
4y - 1 = 7x
When these equations are solved graphicaly, we have
(x, y) = (5, 9)
Hence, the equations are x² = y + 16 & 4y - 1 = 7x and the solution is (5, 9)
Read more about system of equations at
https://brainly.com/question/13729904
#SPJ1
what is 6pints equal to in cups ?
Answers
Answer: 12 cups
Step-by-step explanation:
Answer:
12 cups
Step-by-step explanation:
1 pint = 2 cups
6 pints = 6 × 2 cups = 12 cups
How do you determine if a matrix is a linear combination of other matrices?
Answers
To determine if a matrix is a linear combination of other matrices, we need to check if it can be written as a weighted sum of those matrices where the weights are scalar values (numbers).
If a matrix can be expressed in this way, it is said to be a linear combination of the other matrices.
For example if we have matrices: A, B & C and we can write matrix D as follows:
D = 2A + 3B + CThen D is a linear combination of matrices A, B and C. This concept is important in linear algebra as it allows us to express one matrix in terms of others. Making it easier to manipulate & analyze the matrices. A matrix is a linear combination of other matrices if it can be expressed as a weighted sum of those matrices where the weights are scalar values.
Learn more about linear combination brainly.com/question/8881662
#SPJ4
Solve the equation. Give an exact solution, and also approximate the solution to four decimal places.
7ˣ⁺³=2
log2⁽ˣ⁺³⁾⁼⁵ Select the correct choice below and fill in any answer boxes present in your choice. A. X= (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) B. There is no solution.
Answers
The equation 7^(x+3) = 2log2^(x+3) has no exact solution. Therefore, the correct choice is B. There is no solution.
To solve the equation 7^(x+3) = 2log2^(x+3), we need to isolate the variable x. However, we notice that the equation involves both exponential and logarithmic terms, which makes it challenging to find an exact solution algebraically.
Taking the logarithm of both sides can help simplify the equation:
log(7^(x+3)) = log(2log2^(x+3))
Using the properties of logarithms, we can rewrite the equation as:
(x+3)log(7) = log(2)(log2^(x+3))
However, we still have logarithmic terms with different bases, making it difficult to find an exact solution algebraically.
To approximate the solution, we can use numerical methods such as graphing or iterative methods like the Newton-Raphson method. Using these methods, we find that the equation does not have a real-valued solution. Therefore, the correct choice is B. There is no solution.
Learn more about Newton-Raphson method here:
https://brainly.com/question/13263124
#SPJ11
Select either relation (if the set is a relation but not a function), function (if the set is both a relation and a functions, or
neither (if the set is not a relation).
F=[lxy) x+y=10)
Answers
Answer:
I believe the answer is function
Step-by-step explanation:
HELP ME PLEASE!!! what’s the similarity statement and what is SF=

Answers
A similarity statement is a statement used in geometry to prove exactly why two shapes have the same shape and are in proportion.
f(x) = -x + 5
g(x) = x2 – x +4
Find: (f•g)(x)

Answers
Answer:
\((fog)(x) = - {x}^{2} + x + 9\)
Step-by-step explanation:
\((fog)(x) = f(g(x)) \\ = - ( {x}^{2} - x - 4) + 5 \\ = - {x}^{2} + x + 4 + 5 \\ = - {x}^{2} + x + 9\)
I hope I helped you^_^
Prove n7 ≤ 2n for n ≥ 37.
(a) Use induction
(b) Use leaping induction
Answers
(a) Using induction: n^7 ≤ 2^n for n ≥ 37. (b) Using leaping induction: n^7 ≤ 2^n for n ≥ 37.(a) Using induction, we can prove that n^7 ≤ 2^n for n ≥ 37.
Base Case: For n = 37, we have 37^7 = 69,343, while 2^37 ≈ 137,438,953,472. Since 69,343 ≤ 137,438,953,472, the base case holds.
Inductive Step: Assume that for some k ≥ 37, k^7 ≤ 2^k. We need to show that (k + 1)^7 ≤ 2^(k + 1).
Expanding (k + 1)^7 using the binomial theorem, we have:
(k + 1)^7 = C(7, 0)k^7 + C(7, 1)k^6 + C(7, 2)k^5 + C(7, 3)k^4 + C(7, 4)k^3 + C(7, 5)k^2 + C(7, 6)k + C(7, 7)
Since k ≥ 37, each term in the expansion is multiplied by a positive coefficient. Thus, we can rewrite the inequality as:
(k + 1)^7 ≤ 2k^7 + 2k^6 + 2k^5 + 2k^4 + 2k^3 + 2k^2 + 2k + 2
By the induction hypothesis, k^7 ≤ 2^k, so we can substitute this in the inequality:
(k + 1)^7 ≤ 2^k + 2k^6 + 2k^5 + 2k^4 + 2k^3 + 2k^2 + 2k + 2
Now, we need to prove that 2^k + 2k^6 + 2k^5 + 2k^4 + 2k^3 + 2k^2 + 2k + 2 ≤ 2^(k + 1).
Dividing both sides by 2, we have:
2^k + k^6 + k^5 + k^4 + k^3 + k^2 + k + 1 ≤ 2^k
Since k ≥ 37, each term on the left-hand side is positive, and the inequality holds.
Therefore, we have shown that if k^7 ≤ 2^k for some k ≥ 37, then (k + 1)^7 ≤ 2^(k + 1).
By the principle of mathematical induction, we can conclude that n^7 ≤ 2^n for n ≥ 37.
Keywords: induction, n^7, 2^n, base case, inductive step, binomial theorem, induction hypothesis.
(b) Using leaping induction, we can prove that n^7 ≤ 2^n for n ≥ 37.
For this approach, we'll use a different base case and an alternative inductive step.
Base Case: For n = 37, we have 37^7 = 69,343, while 2^37 ≈ 137,438,953,472. Since 69,343 ≤ 137,438,953,472, the base case holds.
Inductive Step: Instead of considering (k + 1), we'll consider (k + 7) in each step.
Assume that for some k ≥ 37, k^7 ≤ 2^k. We need to show that (k + 7)^7 ≤ 2^(k + 7).
Expanding (k + 7)^7 using the bin
omial theorem, we have:
(k + 7)^7 = C(7, 0)k^7 + C(7, 1)k^6(7) + C(7, 2)k^5(7^2) + ... + C(7, 6)k(7^6) + C(7, 7)(7^7)
Now, we can observe that each term in the expansion contains a factor of 7 raised to some power, while k^7 ≤ 2^k. Thus, we can rewrite the inequality as:
(k + 7)^7 ≤ 2^k + 7^1(7^6) + 7^2(7^5) + ... + 7^6(7^1) + 7^7
Simplifying further, we have:
(k + 7)^7 ≤ 2^k + 7^7(1 + 7 + 7^2 + ... + 7^5 + 7^6)
Since k ≥ 37, we know that k ≤ 7k. Therefore, we can rewrite the inequality as:
(k + 7)^7 ≤ 2^k + 7^7(1 + 7 + 7^2 + ... + 7^5 + 7^6) ≤ 2^k + 7^7(7^6 + 7^6 + ... + 7^6 + 7^6) = 2^k + 7^7(7^6 × 6)
By the induction hypothesis, k^7 ≤ 2^k, so we can substitute this in the inequality:
(k + 7)^7 ≤ 2^k + 7^7(7^6 × 6) ≤ 2^k + 7^7(2^k × 6)
Combining the terms, we have:
(k + 7)^7 ≤ (2^k + 7^7(2^k × 6)) = 2^k(1 + 7^7 × 6)
Since 1 + 7^7 × 6 is a constant, we can denote it as C. Therefore, we have:
(k + 7)^7 ≤ 2^k × C = 2^(k + 7)
Hence, we have shown that if k^7 ≤ 2^k for some k ≥ 37, then (k + 7)^7 ≤ 2^(k + 7).
By the principle of leaping induction, we can conclude that n^7 ≤ 2^n for n ≥ 37.
Keywords: leaping induction, n^7, 2^n, base case, inductive step, binomial theorem, induction hypothesis.
Learn more about induction here
https://brainly.com/question/29503103
#SPJ11
A line passes through the points (8, 8) and (4, 0). What is its equation in slope-intercept form?
Answers
Explanation: (8,8) 8-4 and 8-0
- (4,0)- 4 8
- you take the 8 as the numerator and 4 and the denominator and then divide 8 by 4 to=2 which is your slope
- you pick 1 set of points (I chose (8,8) to finish the problem)
8(y-intercept)= 2(slope) • 8(x-intercept) +b
8= 16+b
-16 -16 (subtract 16 from both sides)
-8 (8-16) =b {b=-8)
-now you put together your equation,
which leaves you with { y=2(x) - 8}
^ ^
your slope your B value
A window has the shape of a rectangle surmounted by a regular triangle. If the perimeter of the window is p, and the base of the rectangle is x, show that in order to obtain a window of maximum area, the following relation must be satisfied X= 1/33 (6+√3) p
Plssss I need help Asap
Answers
Answer: Let's assume that the base of the rectangle is "x", and the height of the rectangle is "y". Let's also assume that the side length of the equilateral triangle is "t".
Then, we can write the perimeter of the window as:
p = x + 2y + 3t
We want to find the value of "x" that maximizes the area of the window. The area of the window can be expressed as:
A = xy + (1/2) * t * sqrt(3) * t
where the first term represents the area of the rectangle and the second term represents the area of the equilateral triangle.
To simplify the expression, we can use the perimeter equation to eliminate "y" and "t". Solving for "y", we get:
y = (1/2) * (p - x - 3t)
Solving for "t", we get:
t = (1/3) * (p - x - 2y)
Substituting these expressions into the area equation, we get:
A = x/2 * (p - x - 2y) + (1/6) * (p - x - 2y)^2 * sqrt(3)
Expanding this expression and simplifying, we get:
A = (1/12) * (p^2 - 2px + 3x^2) * sqrt(3) + (1/2) * px - (1/2) * x^2
To find the value of "x" that maximizes this expression, we can take the derivative of "A" with respect to "x" and set it equal to zero:
dA/dx = (1/12) * (6x - 2p) * sqrt(3) + (1/2) * p - x = 0
Simplifying this expression, we get:
x = (1/33) * (6 + sqrt(3)) * p
Therefore, in order to obtain a window of maximum area, the base of the rectangle should be equal to (1/33) * (6 + sqrt(3)) times the perimeter of the window.
This took a while brainliest would be appreciated (:
Note: Enter your answer and show all the steps that you use to solve this problem in the space provided.
Use the circle graph shown below to answer the question.
A pie chart labeled Favorite Sports to Watch is divided into three portions. Football represents 42 percent, baseball represents 33 percent, and soccer represents 25 percent.
If 210 people said football was their favorite sport to watch, how many people were surveyed?
Natalie picked 135 berries in 15 minutes. If she continues picking at that rate, how many total minutes will it take her to pick 486 berries?
a. Find the unit price for each option shown below. Round to the nearest cent when necessary.
Option I: 10 candy bars for $6.75
Option II: 12 candy bars for $7.25
b. Which option is the better buy.
Solve the proportion.
16
50
=
x
156
.
25
A jacket's original price is $65.00. It is on sale for 40% off. You have to pay 5% sales tax. What is the final price for the jacket?
Answers
A) 500
B) 54 minutes
C) 68cents and 60 cents
D)
E) $40.95
ProportionsA proportion is a statement that says that two ratios are equal. They can be used in many everyday situations like comparing sizes, cooking, calculating percentages, and more.
Proportions can be written as equivalent fractions or as equal ratios.
A) 42% = 210
100% = (210 x 100)/42
= 500 people
B) 135 berries = 15 minutes
486 berries = ??minutes
= (486 x 15)/135
= 54 minutes
C) unit price = $6.75/10 = 0.675cents or 68cents
ii) unit price = $7.25/12 = 0.604cents or 60cents
D) Inconclusive question.
E) 40% of 65 = $26
65 - 26 = $39
Tax = 5% = $1.95
Total = $39 + 1.95
Final Price of jacket = $40.95
To learn more on proportions, read it here https://www.bing.com/ck/a?!&&p=7a2fadec0f3811c8JmltdHM9MTY3Njg1MTIwMCZpZ3VpZD0wZWI0MGNjYi04NDg2LTY1ZTgtMzE4OS0xZTczODU5YjY0YmQmaW5zaWQ9NTE3NQ&ptn=3&hsh=3&fclid=0eb40ccb-8486-65e8-3189-1e73859b64bd&psq=proportions+site%3ahttps%3a%2f%2fbrainly.com+in+text%3a+verified+maths&u=a1aHR0cHM6Ly9icmFpbmx5LmNvbS9xdWVzdGlvbi8xMDYwOTk5Ng&ntb=1
#SPJ1
Determine if the following is a rotation or a translation and then find the degree or distance of it.
please help me and provide explanation you will get marked as brainlist

Answers
Answer:
hi my name is chelsea and i wiuld like ti thank yiu fir the points
Answer:
180 deg rotation
Step-by-step explanation:
You can't simply translate the original figure into its image. You'd need a reflection or a rotation. For example, if you reflected triangle HTY over the x-axis, and then reflected it over the y-axis, you'd get triangle H'T'Y. The problem does not allow for reflections, so this cannot be used. That means you must use a rotation.
Use the origin as the center of rotation.
Rotate triangle HTY 180 degrees clockwise or counterclockwise.
You end up with the image.
Answer: 180 deg rotation
Anyone please, I need help on my last question

Answers
Answer: They are congruent
Step-by-step explanation:
All angles are the same, meaning all sides must be in scale to each other, aka they are congruent!
Answer:
answer is non of above.
Step-by-step explanation:
i. they are similar triangles cause all their angles are same.
ii. they can't be congruent; for being congruent they must show ASA, SSS, SAS axioms(which they don't)
iii. they don't have same sizes(implies they can't have same area)
triangle ABC is a right triangle whose right angle is
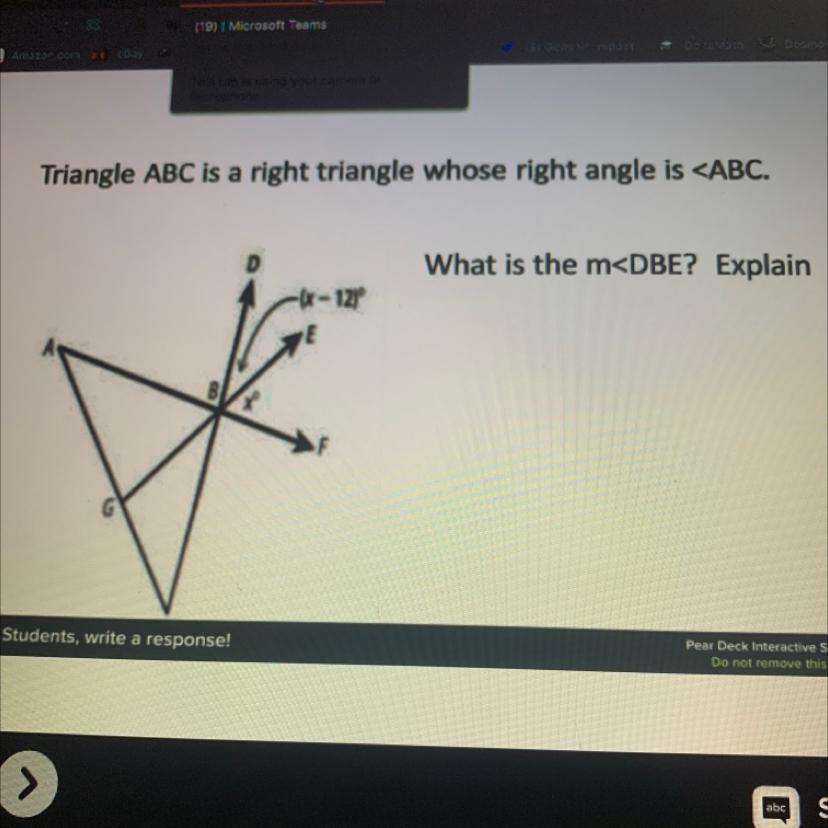
Answers
If triangle ABC is a right triangle and
A half circle has 180 degrees, so the sum of \(\begin{gathered} 90\text{ + (}x\text{-12)}+x\text{ = 180 } \\ x\text{ - 12 + x = 180 - 90 } \\ 2x\text{ - 12 = 90} \\ 2x\text{ = 90 + 12} \\ 2x\text{ = 102} \\ x=\text{ 102/2 } \\ x=\text{ 51º} \end{gathered}\)So, if x= 51º, then m


A single-engine plane can travel up to 140 miles per hour. The total number of miles m is represented by the function m = 140h, where h is the number of hours traveled. Determine appropriate input values for this situation.
Answers
Answer: The input values for this function are the number of hours traveled, represented by the variable h. Therefore, appropriate input values for this function would be any positive number representing a number of hours traveled.
For example, some appropriate input values could be:
h = 1: This represents 1 hour of travel, or a total distance of 140 miles.
h = 2: This represents 2 hours of travel, or a total distance of 280 miles.
h = 3.5: This represents 3.5 hours of travel, or a total distance of 490 miles.
Note that the input values do not have to be whole numbers, they can be any positive number representing a number of hours traveled.
Step-by-step explanation:
What is the slope of the line that contains the points (-2, 2) and (3, 4)?
Answers
Answer:
slope = \(\frac{2}{5}\)
Step-by-step explanation:
calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 2, 2 ) and (x₂, y₂ ) = (3, 4 )
m = \(\frac{4-2}{3-(-2)}\) = \(\frac{2}{3+2}\) = \(\frac{2}{5}\)
Use the function below to find f(-4).
fx) = 2^x
Answers
Answer:
1/16
Step-by-step explanation:
plug in -4 instead of the x.
if the exponent is negative it can be written as 1/2^4
so the answer is 1/16