Match each expression with its factored form.
3x + 9
5x + 15
8x - 20
12x - 20
Answers
The factored forms of the expressions are: 3x + 9 = 3(x + 3), 5x + 15 = 5(x + 3), 8x - 20 = 4(2x - 5), 12x - 20 = 4(3x - 5).
To find the factored form of each expression, we need to factor out the greatest common factor (GCF) from each expression. Let's factor out the GCF for each expression:
3x + 9:
The GCF of 3x and 9 is 3.
Factored form: 3(x + 3)
5x + 15:
The GCF of 5x and 15 is 5.
Factored form: 5(x + 3)
8x - 20:
The GCF of 8x and 20 is 4.
Factored form: 4(2x - 5)
12x - 20:
The GCF of 12x and 20 is 4.
Factored form: 4(3x - 5)
Learn more about greatest common factor:
https://brainly.com/question/29584814
#SPJ11
Related Questions
III Question 4 of 10 ( point) Question Attempt: 1 of Unlimited Susan makes house calls. For each, she is paid a base amount and makes additional money for each hour she works, The graph below shows her pay in dollars) versus the number of hours worked. Use the graph to answer the questions.

Answers
Answer:
a) $30
b) 30
Step-by-step explanation:
a) Her starting pay is $60. After an hour it goes up to $90. 90-60=30.
b) Every hour, the pay goes up 30. Slope is calculated as the change in y divided by the change in x. That means 30/1, or just 30 is the slope.
Identify the equation in slope-intercept form for the line containing the point (2,1) and parallel to y=5/3x−1/3.

Answers
Answer:
A
Step-by-step explanation:
What is the equation of the line that passes through the point (−8,−7) and has a slope of 1?
Answers
Answer:
y = x + 1
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
here m = 1 , then
y = x + c ← is the partial equation
To find c substitute (- 8, - 7 ) into the partial equation
- 7 = - 8 + c ⇒ c = - 7 + 8 = 1
y = x + 1 ← equation of line
4,362,784 rounded to the greatest place value is?
Answers
Answer: 4,000,000
Step-by-step explanation:
4 is the greatest in place values. 3 is lower than 5 so 4 stays the same.
Answer:
The answer is 4,000,000.
Step-by-step explanation:
The greatest place value is the digit closest to the left. 4,362,784 rounded to the closest million is 4,000,000.
please help me its almost due and cant do it
15 points

Answers
Let A=18.0i−52.0
i
^
and B=55.0
i
^
−35.0
k
^
. Find the vector C such that A+B+C=0
18.0
i
^
+107
i
^
−0.0
k
^
18.0
i
^
+107
i
^
−35.0
k
^
−18.0
i
^
+3.00
j
^
+35.0
k
^
−18.0
i
^
−3.00
j
^
+35.0
k
^
Answers
There is no vector C that satisfies the equation A + B + C = 0 in this case. To find the vector C such that A + B + C = 0, we need to manipulate the given equation to solve for C.
Given: A = 18.0i - 52.0j, B = 55.0i - 35.0k
Let's set up the equation A + B + C = 0 and substitute the given values:
18.0i - 52.0j + 55.0i - 35.0k + C = 0
To solve for C, we need to isolate it on one side of the equation. Group the terms with similar components together:
(18.0i + 55.0i) - 52.0j - 35.0k + C = 0
Combine the like terms:
73.0i - 52.0j - 35.0k + C = 0
Now, equate the coefficients of the corresponding unit vectors on both sides of the equation:
73.0i = 0i => 73.0 = 0 (for i-component)
-52.0j = 0j => -52.0 = 0 (for j-component)
-35.0k = 0k => -35.0 = 0 (for k-component)
We can see that these equations are not satisfied since 73.0, -52.0, and -35.0 are not equal to zero. Therefore, there is no vector C that can satisfy the equation A + B + C = 0.
Hence, there is no solution for vector C in this case.
Learn more about coefficients here: https://brainly.com/question/31903177
#SPJ11
Please answer ASAP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer: 75.2
Step-by-step explanation:
Well, if it isn't the most confusing question ever.
First of all, what is P?
I'll assume its the perimeter...
2*(1.2*2)+4*(8.8*2)
Or
2*2.4+4*17.6
75.2
let x and y be two independent random variables with distribution n(0,1). a. find the joint distribution of (u,v), where u
Answers
To find the joint density function, we need to calculate the Jacobian determinant of the transformation from (x, y) to (u, v)
The joint distribution of (u, v), where u and v are defined as
\(u = \frac{x}{{\sqrt{x^2 + y^2}}}\) and \(v = \frac{y}{{\sqrt{x^2 + y^2}}}\), is given by:
\(f_{U,V}(u,v) = \frac{1}{{2\pi}} \cdot e^{-\frac{1}{2}(u^2 + v^2)}\)
To find the joint density function, we need to calculate the Jacobian determinant of the transformation from (x, y) to (u, v):
\(J = \frac{{du}}{{dx}} \frac{{du}}{{dy}}\)
\(\frac{{dv}}{{dx}} \frac{{dv}}{{dy}}\)
Substituting u and v in terms of x and y, we can evaluate the partial derivatives:
\(\frac{{du}}{{dx}} &= \frac{{y}}{{(x^2 + y^2)^{3/2}}} \\\frac{{du}}{{dy}} &= -\frac{{x}}{{(x^2 + y^2)^{3/2}}} \\\frac{{dv}}{{dx}} &= -\frac{{x}}{{(x^2 + y^2)^{3/2}}} \\\frac{{dv}}{{dy}} &= \frac{{y}}{{(x^2 + y^2)^{3/2}}}\)
Therefore, the Jacobian determinant is:
\(J &= \frac{y}{{(x^2 + y^2)^{\frac{3}{2}}}} - \frac{x}{{(x^2 + y^2)^{\frac{3}{2}}}} \\&= -\frac{x}{{(x^2 + y^2)^{\frac{3}{2}}}} + \frac{y}{{(x^2 + y^2)^{\frac{3}{2}}}} \\J &= \frac{1}{{(x^2 + y^2)^{\frac{1}{2}}}}\)
Now, we can find the joint density function of (u, v) as follows:
\(f_{U,V}(u,v) &= f_{X,Y}(x,y) \cdot \left|\frac{{dx,dy}}{{du,dv}}\right| \\&= f_{X,Y}(x,y) / J \\&= f_{X,Y}(x,y) \cdot (x^2 + y^2)^{\frac{1}{2}}\)
Substituting the standard normal density function
\(f_{X,Y}(x,y) &= \frac{1}{2\pi} \cdot e^{-\frac{1}{2}(x^2 + y^2)} \\f_{U,V}(u,v) &= \frac{1}{2\pi} \cdot e^{-\frac{1}{2}(x^2 + y^2)} \cdot (x^2 + y^2)^{\frac{1}{2}} \\&= \frac{1}{2\pi} \cdot e^{-\frac{1}{2}(u^2 + v^2)}\)
Therefore, the joint distribution of (u, v) is given by:
\(f_{U,V}(u,v) &= \frac{1}{2\pi} \cdot \exp\left(-\frac{1}{2}(u^2 + v^2)\right)\)
Learn more about joint probability distributions:
https://brainly.com/question/32099581
#SPJ11
To find the joint density function, we need to calculate the Jacobian determinant of the transformation from (x, y) to (u, v)
The joint distribution of (u, v) is a bivariate normal distribution with mean (0,0) and variance-covariance matrix
\(\begin{bmatrix}2 & 0 \0 & 2\end{bmatrix}\)
The joint distribution of (u, v) can be found by transforming the independent random variables x and y using the following formulas:
\( u = x + y\)
\( v = x - y \)
To find the joint distribution of (u, v), we need to find the joint probability density function (pdf) of u and v.
Let's start by finding the Jacobian determinant of the transformation:
\(J = \frac{{\partial (x, y)}}{{\partial (u, v)}}\)
\(= \frac{{\partial x}}{{\partial u}} \cdot \frac{{\partial y}}{{\partial v}} - \frac{{\partial x}}{{\partial v}} \cdot \frac{{\partial y}}{{\partial u}}\)
\(= \left(\frac{1}{2}\right) \cdot \left(-\frac{1}{2}\right) - \left(\frac{1}{2}\right) \cdot \left(\frac{1}{2}\right)\)
\(J = -\frac{1}{2}\)
Next, we need to express x and y in terms of u and v:
\(x = \frac{u + v}{2}\)
\(y = \frac{u - v}{2}\)
Now, we can find the joint pdf of u and v by substituting the expressions for x and y into the joint pdf of x and y:
\(f(u, v) = f(x, y) \cdot |J|\)
\(f(u, v) = \left(\frac{1}{\sqrt{2\pi}}\right) \cdot \exp\left(-\frac{x^2}{2}\right) \cdot \left(\frac{1}{\sqrt{2\pi}}\right) \cdot \exp\left(-\frac{y^2}{2}\right) \cdot \left|-\frac{1}{2}\right|\)
\(f(u, v) = \frac{1}{2\pi} \cdot \exp\left(-\frac{u^2 + v^2}{8}\right)\)
Therefore, the joint distribution of (u, v) is given by:
\(f(u, v) = \frac{1}{2\pi} \cdot \exp\left(-\frac{{u^2 + v^2}}{8}\right)\)
In summary, the joint distribution of (u, v) is a bivariate normal distribution with mean (0,0) and variance-covariance matrix
\(\begin{bmatrix}2 & 0 \0 & 2\end{bmatrix}\)
Learn more about joint probability distributions:
brainly.com/question/32099581
#SPJ11
BP has a bond outstanding with 15 years to maturity, a $1,000 par value, a coupon rate of 6.9%, with coupons paid semiannually, and a price of 98.17 (percent of par) 18 | Attempt 1/10 for 10 pts. Part 1 What is the cost of debt?
Answers
There is an outstanding bond from BP with a 15-year maturity, a $1,000 par value, a 6.9% coupon rate that is paid semi-annually, and a price of 98.17. As a result, the annual cost of debt for this bond is roughly 8.5 percent.
To calculate the cost of debt, we need to determine the yield to maturity (YTM) of the bond. The YTM is the rate of return an investor would earn by purchasing the bond and holding it until maturity. We can use the bond pricing formula to calculate the YTM.
The bond pricing formula is as follows:
\(\text{Bond Price} = \frac{{C \times (1 - (1 + r)^{-n})}}{{r}} + \frac{{M}}{{(1 + r)^n}}\)
Where:
C = Coupon payment
r = Yield to maturity (YTM)
n = Number of periods
M = Par value
Given information:
Coupon payment (C) = \(\$1,000 \times \frac{6.1\%}{2} = \$30.50\)
Par value (M) = $1,000
Bond price = $1,000 × 83.57% = $835.70
We know the bond has 15 years to maturity, and coupons are paid semiannually. So, the number of periods (n) is 15 years × 2 = 30.
Using the bond pricing formula, we can rearrange it to solve for the YTM:
\(Bond Price = \frac{{C \times (1 - (1 + r)^{-n})}}{{r}} + \frac{{M}}{{(1 + r)^n}}\)
Substituting the given values:
\($835.70 = \left(\frac{{\$30.50 \times (1 - (1 + r)^{-30})}}{{r}}\right) + \left(\frac{{\$1,000}}{{(1 + r)^{30}}}\right)\)
To find the YTM, we need to solve this equation either algebraically or using numerical methods like trial and error or using financial calculators/spreadsheets.
By using a financial calculator or spreadsheet, we find that the YTM is approximately 8.5%. Therefore, the cost of debt for this bond is approximately 8.5% per year.
To know more about the yield to maturity refer here :
https://brainly.com/question/26376004#
#SPJ11
Complete question :
Problem 17 Intro BP has a bond outstanding with 15 years to maturity, a $1,000 par value, a coupon rate of 6.1%, with coupons paid semiannually, and a price of 83.57 (percent of par). | Attempt 1/10 for 10 pts. Part 1 What is the cost of debt? B+ decimals Submit
is the following graph a function?
A. yes
B. no

Answers
Answer:
Yes
Step-by-step explanation:
You can use the Vertical line test to figure this out, and sure enough none of the points touch the vertical line.
Everything is in question

Answers
Subtract 2 on both sides
w/-1 _> -5
Inverse of w/-1
(-1/w)w/-1 _> (-1)-5
w _> 5
40.82 divided by 13 please answer quick
Answers
Answer:
3.14
Step-by-step explanation:
03.14 is your answer
help me with this please

Answers
The values of a, b, c are 152°, 28°, 152° respectively.
What are angle at a point?Angles around a point describes the sum of angles that can be arranged together so that they form a full turn.
The sum of angles at a point will give 360°.
This means that a + b + c + 28 = 360
c +28 = 180° ( angle on a straight line)
c = 180 -28
c = 152°
c = a( alternate angles are equal)
therefore the value of a = 152°
b = 28( alternate angles are equal)
therefore the value of b is 28
therefore the values of a, b, c are 152°, 28°, 152° respectively
learn more about angle at a point from
https://brainly.com/question/25716982
#SPJ1
find the finance charge for a $25,000, three year loan with a 9.25% apr. How much interest is paid
Answers
Answer:
$6,937.50
Step-by-step explanation:
Interest = Principal x Rate x Time
I = 25000(.0925)(3)
The area of the base is 7 cm. What is the surface area of the pyramid?

Answers
Answer: 34.5
Step-by-step explanation:
(Base · Height) ÷ 2 → (2 · 4.5) ÷ 2 = 5.5
5.5 · 5 = 27.5
27.5 + 7 = 34.5
\Plot the point (4, −3).
Start at the origin.
Move 4 units
Move 3 units
The point is at ___
Model |
^
On a coordinate plane, point A is 4 units to the left and 3 units up. Point B is 3 units to the left and 4 units up. Point C is 4 units to the right and 3 units up. Pound D is 4 units to the right and 3 units down.
Answers
The points A(-4,3) ; B(-3,4) ; C(4,3) ; D(4,-3) are plotted on the graph.
What is meant by a coordinate plane?
Two number lines combine to generate the two-dimensional surface known as the coordinate plane. The x-axis is a single horizontal number line. The y-axis is the name of the vertical number line which is the other number line. The origin is where the two axes come together. The coordinate plane can be used to graph points, lines, and other things.
The given points are
A is 4 units to the left and 3 units up which means A is (-4,3).
B is 3 units to the left and 4 units up which means B is (-3,4).
C is 4 units to the right and 3 units up which means C is (4,3).
D is 4 units to the right and 3 units down which means D is (4,-3).
All these 4 points are plotted on the coordinate plane and the graph is attached below.
To learn more about plotting points, refer to the link below:
https://brainly.com/question/27481419
#SPJ1

Rsound answer to two decimal places
80.75757575757575757575
Answers
Answer:
\(80. \bar{75}\)
Find the value of x. If necessary, write your answer in simplest radical form.
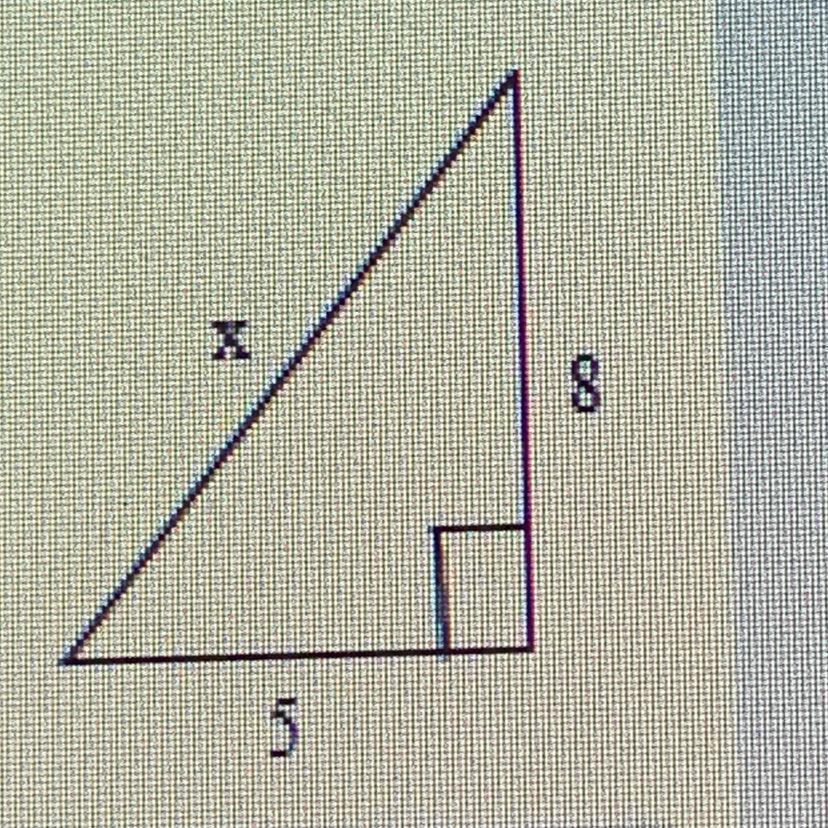
Answers
Answer:
Step-by-step explanation:
1 Warm-Up Go to formulas page and write out Pythagorean Theorem. ... Example 1B: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 (x – 2)2 + 42 = x2 x2 – 4x + 4 + 16 = x2 ... safety ratio of 4:1, how high will a 30-foot ladder reach when placed against a wall?
Which statement shows correct reasoning for finding 12+3/8? A Multiply 12 by 8, then divide by 3. B. Multiply 12 by 3, then divide by 8. C. Multiply 3 by 8, then divide by 12 D. Multiply 12 by 1/8, then multiply by 3.
Answers
Answer:
B
Step-by-step explanation:
plz mark the brainliest. if that is adding not multiplying, you will do 3 divide by 8 first and then add 12. I think its a typo and it is multiply so if it is multiply, it is B. plz mark the brainliest
Quadrilateral ABCD is dilated with center
( 0, 0 ), taling B to B' . Draw A' B' C' D' .

Answers
Answer:
See the picture below
Step-by-step explanation:

Which choice gives the solution of this inequality? 3t+ < 28
Answers
Answer:
its 9.33 reapetting or just 9.33
Step-by-step explanation:
m angle KHG= (4x+6) and m angle HGW= (6x-16) and m angle NGX=(y+9)
5. Find the value of x
6. Find the value of y
7. m angle KHG=
8. m angle HGW=
9. m angle NGX=

Answers
Question 5
Using the alternate interior angles theorem,
\(4x+6=6x-16\\\\6=2x-16\\\\22=2x\\\\x=11\)
Question 6
Using the corresponding angles theorem,
\(4x+6=y+9\\\\4(11)+6=y+9\\\\50=y+9\\\\y=41\)
Question 7
\(m\angle KHG=4(11)+6=50^{\circ}\)
Question 8
\(m\angle HGW=6(11)-16=50^{\circ}\)
Question 9
\(m\angle NGX=41+9=50^{\circ}\)
henry scored 85, 76, 84, and 69 on four exams. what must he make on the fifth exam to have an average of 80?
Answers
Henry must have to score 86 marks in the fifth exam to make an average of 80 marks.
What is the average?
This is the arithmetic mean and is calculated by adding a group of numbers and then dividing by the count of those numbers. For example, the average of 2, 3, 3, 5, 7, and 10 is 30 divided by 6, which is 5.
Henry scored 85, 76, 84, and 69, and let's suppose he scored 'x' marks in the fifth exam.
Average = sum of all marks/total number of exams
80 =(85 + 76 + 84 + 69 + x)/5
80 = 314 + x/5
80 * 5 = 314 + x
400 = 314 + x
x = 400 - 314
x = 86
Hence, Henry must have to score 86 marks in the fifth exam to make an average of 80 marks.
To learn more about average in mathematics, visit:
https://brainly.com/question/20118982
#SPJ4
One side of a rectangle has length 4. Another side has length 6+7. What expression represents the area of the rectangle? 4×6+4×7 4×6 4×7 4×6×7.
A. 4×6×7
B. 4×6
C. 4×6+4×7
D. 4×7
Answers
Answer:
C
Step-by-step explanation:
So area is length times width for the rectangle and your length is 4 and your width is 6+7, if you do 4 times 6+7 you will get 52. If you want to be sure you can go down the answer options and do them until you find one that equals 52 which in this case is C.
4 x (6+7) = area
(in case you need the equation)
John played 8 games of basketball this season. In his first 2 games, he averaged 5 more points scored than he did in the next 6 games. If he scored 90 points during the 8 game stretch, then how many points did he score in the first two games of the season, added together?
HELP FASTTTT I need the work for this problem
Answers
Answer:
30Step-by-step explanation:
Let the average score in the last 6 games be x, then average score in first 2 games is x + 5
Considering the total score of 90 solve for x the equation:
2(x + 5) + 6x = 902x + 10 + 6x = 908x = 80x = 10In the first 2 games John's score was:
2(10 + 5) = 30Order each set of integers from least to greatest (15, 17, 21, 6,3)
Answers
Answer:
3, 6, 15, 17, 21.
Step-by-step explanation:
Brainliest?
Northern woods furniture is considering adding a cedar picnic table to it’s line of furniture. NWS estimates that it will sell for $50 to distributors. They also estimate that the fixed cost of producing that table will be $13,000 and that the variable cost per table will be $22. Find the total sales they need to break even.
Answers
The break-even point is the point where the profit and the loss are the same (equal). To calculate it, we have the following formula:
\(Break-even=\frac{Fixed\text{ costs}}{Price-Variable\text{ costs}}\)where "Price" denotes the value estimate (per unit) by the company. In this case, such a value is $50. And "Variable costs" denotes the variable cost per table; in this case, it's $22. Then,
\(\text{Break}-\text{even}=\frac{13000}{50-22}=\frac{13000}{28}\approx464.2\)Now, note that the obtained number of sales is not an entire number. In such cases, we choose the next integer (for we prefer no loss); in this particular case, it's 465.
AnswerThe total sales the company needs to break even are 465.
652.3 divided by 10 using the power of ten rules
Answers
= 65.23
:))
Can someone please help me ASAP?? It’s due tomorrow!! I will give brainliest If It’s correct.

Answers
Answer: To match the shapes produced by the slice through the triangular prism, we need to consider the orientation of the slice relative to the prism. Here are the matching options:
A. Perpendicular to the base: Rectangle
B. Parallel to the base: Triangle with dimensions equal to the base
C. Diagonal from vertex to vertex: Triangle with unknown dimensions
if the probability that a particular event occurs is 7/10, what are the odds favoring the event not occurring? express your answer in the form a:b.
Answers
For the probability of any particular event occurring is 7 /10 then odds of favoring the event which is not occurring in the form of a: b is equal to
7 : 3.
As given in the question,
Probability of any particular event occurring is equal to 7 /10
Probability of any particular event not occurring is = 1- (7/10)
= (10 -7) /10
= 3/10
Probability of the odds favoring the events which are not occurring
= (7 /10) / (3/10)
= ( 7 × 10) / (3 × 10)
= 7 /3
Odds favoring the events which are not occurring in the form a: b
= 7 : 3
Therefore, for the probability of any particular event occurring is 7 /10 then odds of favoring the event which is not occurring in the form of a: b is equal to 7 : 3.
Learn more about probability here
brainly.com/question/11234923
#SPJ4