Match the correct items. 1. checkbook record outstanding checks 2. service charge register 3. previous and ending balances reconciliation 4. verifies bank and checkbook balances agree once a month 5. bank statement monthly fee 6. not included in bank statement account summary
Answers
Answer:
I will answer below:
Step-by-step explanation:
Checkbook Record -> Register
Service Charge -> Monthly Fee
Previous and ending balances -> Account Summary
Verifies bank and checkbook
balances agree -> Reconciliation
Bank Statement -> Once a month
Not included in the bank statement -> Outstanding checks
Sorry this is kind of late!
Related Questions
Timothy has two sons, John and paul in four years time, the sum of the ages of John and paul was 44 years while Timothy was 76 years four years ago. John is older than paul. Find the present age of Timothy
Answers
Answer:
32 is the present age of Timothy
Answer:
32
Step-by-step explanation:
Please help ASAP
Will give Brainliest
Want explanation
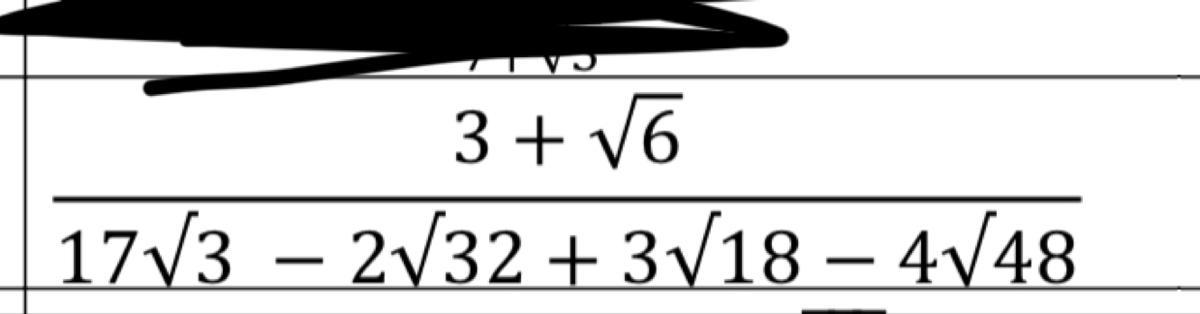
Answers
Answer:
1.73 or 3+√6/√3+√2
Step-by-step explanation:
1. Simplify the Numerator...3+ the square root of 6 cannot be simplified, so the answer is 5.45
2. Simplify the Denominator.
\(17 \sqrt{3} - 2 \sqrt{4} \sqrt{4} \sqrt{2} + 3 \sqrt{9} \sqrt{2} - 4 \sqrt{4} \sqrt{4} \sqrt{3} = 17 \sqrt{3} - 8 \sqrt{2} + 9 \sqrt{2} - 16 \sqrt{3} = \sqrt{3} + \sqrt{2} = 3.15\)
3. Divide. 5.45/3.15= 1.73
Write nine hundred and eight tenths as a decimal number.
Answers
Answer:
900.8
Step-by-step explanation:
hope this helps:)
There are 170 deer on a reservation. The deer population is increasing at a rate of 30% per year
Answers
A function \(P(t) = 170.(1.30)^t\) that gives the deer population P(t) on the reservation t years from now
We were told there were 170 stags on reservation. The number of deer is increasing at a rate of 30% per year.
We could see the deer population grow exponentially since each year there will be 30% more than last year.
Since we know that an exponential growth function is in form:
\(f(x) = a*(1+r)^x\)
where a= initial value, r= growth rate in decimal form.
It is given that a= 170 and r= 30%.
Let us convert our given growth rate in decimal form.
\(30 percent = \frac{30}{100} = 0.30\)
Upon substituting our given values in exponential function form we will get,
\(P(t) = 170.(1+0.30)^t\)
⇒ \(P(t)= 170.(1.30)^t\)
Therefore, the function \(P(t) = 170.(1.30)^t\) will give the deer population P(t) on the reservation t years from now.
Complete Question:
There are 170 deer on a reservation. The deer population is increasing at a rate of 30% per year. Write a function that gives the deer population P(t) on the reservation t years from now.
Learn more about Function:
https://brainly.com/question/12431044
#SPJ4
After a store deducted 15% from the price of a stereo, Charlie paid $123. What was the original price of the stereo?
Answers
Answer:
Step-by-step explanation:
assume x = original price
100% -15%= 75%
75% of x = 123
\(\frac{75}{100} * x = 123\\\\\frac{75x}{100} = 123\\\\75 x = 12300\\x = 164\)
Find the equation of a line that passes through (1,9) and is parallel to the graph of y=3x+4. Write the equation in slope-intercept form, if possible. Select the correct choice below and fill in the answer box to complete your choice. The equation of the parallel line in slope-intercept form is
enter your response here.
(Simplify your answer. Type your answer in slope-intercept form. Use integers or fractions for any numbers in the equation.)
B.
The equation of the parallel line cannot be written in slope-intercept form. The equation of the parallel line is
enter your response here.
(Simplify your answer. Use integers or fractions for any numbers in the equation.)
Answers
Because the slope of Noah Garcia’s nose is bigger
The diagram shows a square with perimeter 20cm.what is a perimeter of the rectangle
Answers
The perimeter of the rectangle is 60 cm.
We have,
The square perimeter = 20 cm
This means,
Each side of the square = 20/4 = 5 cm
Now,
From the rectangle figure,
Length = 5 + 5 + 5 + 5 = 20 cm
Width = 5 + 5 = 10 cm
So,
The perimeter of the rectangle.
= 2 (length + width)
= 2 x (20 + 10)
= 2 x 30
= 60 cm
Thus,
The perimeter of the rectangle is 60 cm.
Learn more about rectangles here:
https://brainly.com/question/15019502
#SPJ1

can someone help quick

Answers
is -6/3 and integer? dont guess ;( helppp
Answers
Answer:
no because
Fractions and decimals are not integers. All whole numbers are integers (and all natural numbers are integers), but not all integers are whole numbers or natural numbers. For example, -5 is an integer but not a whole number or a natural number.
-6/3 is not an integer.
What is Number system?A number system is defined as a system of writing to express numbers.
We need to check whether -6/3 is a integer or not .
An integer is a whole number (not a fractional number) that can be positive, negative, or zero.
The given number is a fraction which is not comes under the integers.
All whole numbers are integers but but not all integers are whole numbers or natural numbers.
If the fraction is simplified we get -2 which will be an integer but the fraction form is not considered as integer.
Hence, -6/3 is not an integer.
To learn more on Number system click:
https://brainly.com/question/2204604
#SPJ2
Shown below is one way to solve 40 ÷ 8.
40 / 8 = ( 32 / 8) + ( 8 / 8 )
= 4 + 1
= 5
Use the given example to solve 30 ÷ 5.
Answers
Answer:
6
Step-by-step explanation:
30:5 = (25:5) + (5:5) = (5x5:5) + (5:5)= 5+1 =6
the length of each side of a square is 3 inches more than the length of each side of a smaller square. the sum of the areas of the squares is 149 inches squared. find the length of the side of the smaller square.
Answers
The length of the side of the smaller square is 7 inches.
Let x be the length of the side of the smaller square.
The length of each side of a square is 3 inches more than the length of each side of a smaller square. Thus the length of the side of the larger square is
(x + 3) inches.
The area of the smaller square is
x^2 square inches.
The area of the larger square is
(x + 3)^2 square inches.
We can set up the equation:
x^2 + (x + 3)^2 = 149
Expanding and simplifying the equation gives:
x^2 + x^2 + 6x + 9 = 149
Combining like terms:
2x^2 + 6x - 140 = 0
Using the quadratic formula, we can solve for x:
x = (-b ± √(b^2 - 4ac)) / 2a
x = (-6 ± √(6^2 - 4 * 2 * (-140))) / 2 * 2
x = (-6 ± √(36 + 1120)) / 4
x = (-6 ± √(1156)) / 4
x = (-6 ± √(596)) / 4
x = (-6 ± 34) / 4
x = -10 or x = 7
The side length of the smaller square can't be negative, so x = 7 inches.
To know more on quadratic formula
https://brainly.com/question/11540485
#SPJ4
IT NOT EIGHT
Factor 56−16 using the GCF.
56−16=
Answers
Answer:
It should be 8...
Step-by-step explanation:
16 / 8 = 2 and there is no higher number 16 that can be divided by. 56 is dividable by 8 so it makes sense.
Also 56 isn't dividable by 16
Ayudaaaa porfa ):porfavor

Answers
The vertices of the dilated image are given.
What is Dilation?Dilation is a type of transformation where the figure is enlarged or made smaller such that it preserves the shape but not size.
Every dilated image are similar figures to the original figure.
The point (x, y) with the scale factor of k will dilate to the vertex (kx, ky) if the center of dilation is origin.
1) Given for ΔQRS, Q(-1, 0), R(-1, 2) and S(-2, 1).
Scale factor = 2
Q'(2×-1, 2×0) = Q'(-2, 0)
R'(2×-1, 2×2) = R'(-2, 4)
S'(2×-2, 2×1) = S'(-4, 2)
2) Given for ΔTRK, T(-1, -2), R(1, 0) AND K(0, 1).
Scale factor = 3
T'(-3, -6), R'(3, 0) and K'(0, 3)
3) Given for ΔXYZ, X(-4, 0), Y(-4, 4) and Z(-2, -2).
Scale factor = 1/2
X'(-2, 0), Y'(-2, 2) and Z'(-1, -1)
4) If the center of dilation is not origin, then,
P'(x, y) = O(x, y) + k [P(x, y) - O(x, y)]
where, P'(x, y) is the dilated point, O(x, y) is the center of dilation, k is the scale factor and P(x, y) is the original point.
Given for ΔHAT, H(-1, -1), A(1, 0) and T(-1, 2).
Scale factor = 2
Center of dilation = (-1, 2)
H'(x, y) = (-1, 2) + 2 [(-1, -1) - (-1, 2)]
= (-1, 2) + 2 (-1+1, -1-2)
= (-1, 2) + 2 (0, -3)
= (-1, 2) + (0, -6)
= (-1, -4)
A'(x, y) = (-1, 2) + 2 [(1, 0) - (-1, 2)]
= (-1, 2) + 2 (2, -2)
= (3, -2)
T'(x, y) = (-1, 2) + 2 [(-1, 2) - (-1, 2)]
= (-1, 2) + 2 (0, 0)
= (-1, 2)
Hence the vertices of the dilated image are found.
Learn more about Dilation here :
https://brainly.com/question/13176891
#SPJ1
The estimate on an explanatory variable is not statistically significant at the 5%-level if the t-statistic is greater than 2.5. the p-value is less than 0.05. the 95% confidence interval does not contain zero. the 95% confidence interval contains zero.
Answers
The estimated value of the explanatory variable is not statistically significant at the 5%-level if a. the t-statistic is greater than 2.5.
The t-test is a hypothesis testing technique used to decide whether the estimated coefficient of a linear regression model is statistically significant or not. The t-value is used to measure the size of the difference between the estimated coefficient and the hypothesized value. When the t-value exceeds a critical value, such as 2.5, the estimated value of the explanatory variable is not significant at the 5%-level. It implies that the null hypothesis, which assumes that the explanatory variable's coefficient is zero, cannot be rejected.
The p-value is a measure of the probability of obtaining a more extreme value of the test statistic than the observed value if the null hypothesis is true. A small p-value implies that the null hypothesis should be rejected. When the p-value is less than 0.05, it means that the estimated value of the explanatory variable is significant at the 5%-level.
The confidence interval is a range of values that is expected to include the true value of the population parameter with a specified level of confidence. A 95% confidence interval means that the true value of the population parameter lies within the range 95% of the time. The 95% confidence interval does not contain zero implies that the estimated value of the explanatory variable is statistically significant at the 5%-level since it suggests that the population parameter is different from zero at the 5%-level. Conversely, if the 95% confidence interval contains zero, the estimated value of the explanatory variable is not statistically significant at the 5%-level since it means that the population parameter is not different from zero at the 5%-level. Therefore, it is essential to examine the t-statistic, p-value, and confidence interval while conducting hypothesis testing to make an informed decision.
To leran more about hypothesis testing, refer:-
https://brainly.com/question/17099835
#SPJ11
is a fraction a term? If it's not a term, why is it that we can apply the distributive property to it? the distributive property only works for either terms, or addition and subtraction. a fraction is technically division, so why does it work? Please help!!!!!
Answers
No, a fraction is not a term. The distributive property can be applied to fractions because it is a general mathematical principle.
A fraction is not considered a term in the traditional sense. It is a mathematical expression that represents division. However, the distributive property can still be applied to fractions because the property itself is a fundamental rule of arithmetic that extends beyond specific types of expressions.
The distributive property states that for any real numbers a, b, and c:
a × (b + c) = (a × b) + (a × c).
When working with fractions, we can apply the distributive property as follows:
Let's consider the expression: a × (b/c).
We can rewrite this as: (a × b)/c.
Now, let's distribute the 'a' to 'b' and 'c':
(a × b)/c = (a/c) × b.
In this step, we applied the distributive property to the fraction (a/c) by treating it as a whole.
Although fractions represent division, we can still use the distributive property because it is a general mathematical principle that allows for manipulating expressions involving addition, subtraction, multiplication, and division.
For more such question on fraction
https://brainly.com/question/17220365
#SPJ8
What is the inverse of the function f(x) = 2x + 1?
h(x) = one-halfx – one-half
h(x) = one-halfx + one-half
h(x) = one-halfx – 2
h(x) = one-halfx + 2
f(–2) = g(–2)
f(0) = g(–2)
f(–2) = g(0)
Answers
The inverse of the function f(x) = 2x+1 is (x-1)/2.
What is inverse of function?The output of a function is returned by the inverse function, which also returns the initial value. Consider the inverse relationship between the functions f and g: f(g(x)) = g(f(x)) = x. The initial value is fetched via a function that is its inverse.
Given;
Function, f(x) = 2x + 1.
To find the inverse of the function:
First, let y = f(x)
That is,
y = 2x +1
Then, make x the subject of the equation
y = 2x + 1
To make x the subject of this equation:
First, subtract 1 from both sides
We get
y -1 = 2x
Now, divide both sides by 2.
x = (y-1)/2
Now, rewrite as f⁻¹(x) by replacing y by x.
That is,
f⁻¹(x) = (x-1)/2
Therefore, the inverse of the function f(x) is (x-1)/2.
To learn more about the inverse of function;
https://brainly.com/question/17872426
#SPJ1
Mom bought gas for $75.00 for 5 gallons. How much is 1 gallon of gas.
Answers
Answer:
15
Step-by-step explanation:
EZZZZZZZZZZZZZZZZZZZZZZZZZ
Answer:
15
Step-by-step explanation:
hdhfddd gotta sg themselves when's high
A rock is dropped from a bridge 128 feet above the river. The pathway that the rock takes can be modeled by the equation h= -16t2+128. How long will it take the rock to reach the river?
Answers
Answer:
2.83 seconds
Step-by-step explanation:
In the given equation, h represents the height (in feet) of the rock above the river at time t seconds after it is dropped, and the equation is h = -16t^2 + 128.
When the rock reaches the river, its height above the river will be zero. So, we can set h = 0 in the equation and solve for t:
0 = -16t^2 + 128
Dividing both sides by -16, we get:
t^2 = 128/16
t^2 = 8
Taking the square root of both sides, we get:
t = ±√8
Since time cannot be negative, we take the positive square root:
t = √8 ≈ 2.83 seconds
Therefore, it will take the rock approximately 2.83 seconds to reach the river.
Explain the error in the work and how you might prevent it
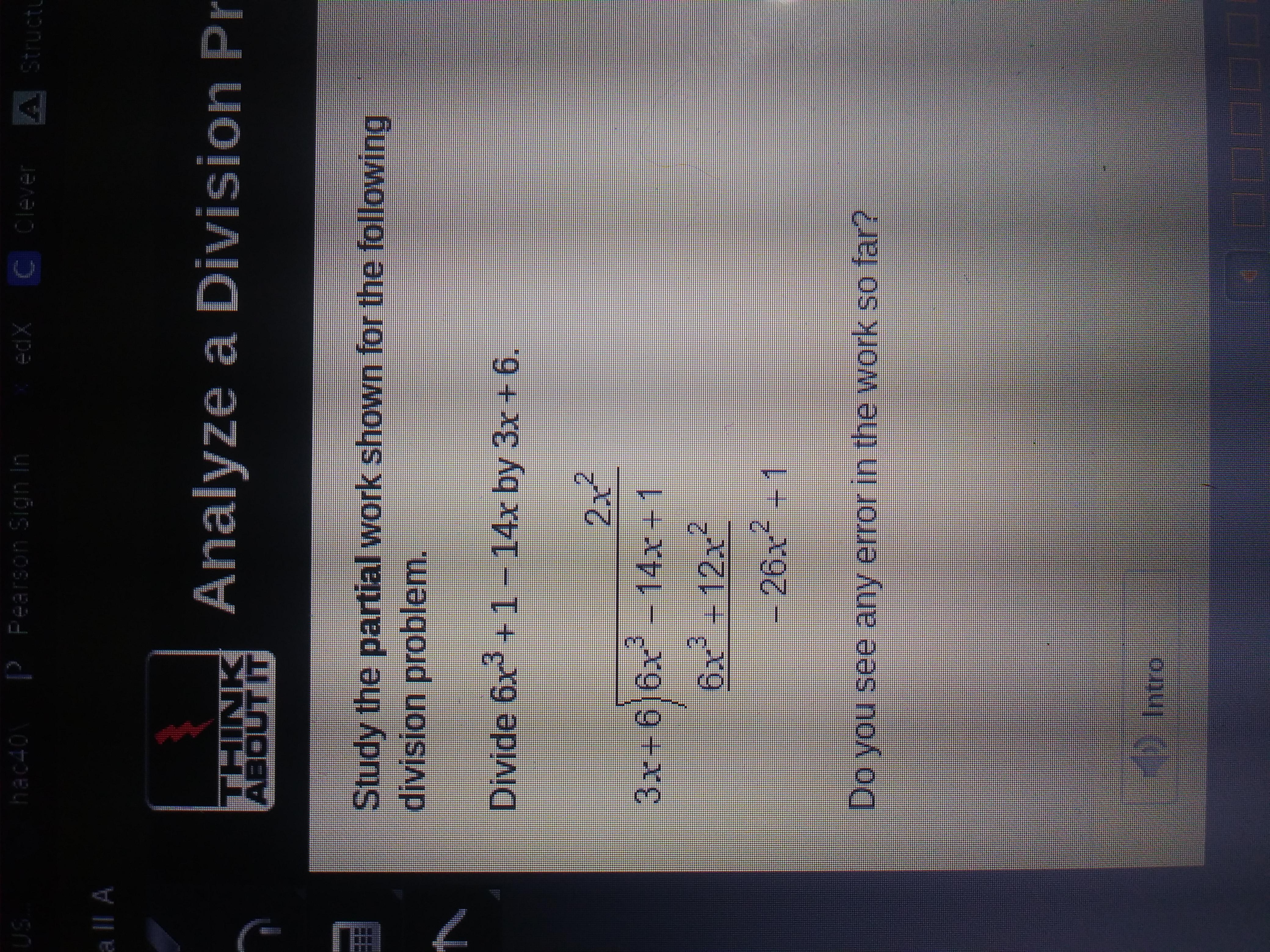
Answers
Answer:
The error is -12x² - 14x = - 26x² because 12x² and 14x are unlike terms, so we can not add them
To prevent it the dividend must be written as 6x³ + 0x² - 14x + 1
Step-by-step explanation:
In the division, you must arrange the dividend according to the greatest power of the variable, and put 0 as a coefficient of the missing term to avoid adding, unlike terms.
Example:
If the dividend is 3x³ - 2x + 5, then you must write it as 3x³ + 0x² - 2x + 5
Let us solve our question
∵ The dividend is 6x³ + 1 - 14x
→ You must arrange it from the greatest power of x
∴ The dividend is 6x³ - 14x + 1
∵ The term of x² is missing
→ Write it in the dividend with a coefficient of 0
∴ The dividend is 6x³ + 0x² - 14x + 1
The error is the adding of unlike terms
∵ 6x³ - 14x + 1 ÷ 3x + 6 = 2x² and [6x³ - 14x + 1 - 6x³ - (6x³ + 12x²)]
∵ [6x³ - 14x + 1 - 6x³ - (6x³ + 12x²)] = 6x³ - 14x + 1 - 6x³ - 12x²
∵ 6x³ - 14x + 1 - 6x³ - 12x² = 0 - 12x² - 14x + 1
∵ 0 - 12x² - 14x + 1 = -26x² + 1 ⇒ error
∴ The error is -12x² - 14x = - 26x² because 12x² and 14x are unlike terms,
so we can not add them
→ To prevent it, write 0 as a coefficient of the missing term
∵ The missing term is the term of x²
∴ Add to the dividend the term 0x²
∴ The dividend must be written as 6x³ + 0x² - 14x + 1
Answer:
-14x and 12x² are not like terms, so they can’t be subtracted.
To prevent this error, be sure to line up like terms
Step-by-step explanation:
just did it
The diagram shows the solid glass case for a clock. The case is a cuboid with a cylinder
removed (to fit the clock mechanism). Calculate the volume of glass required to make the
clock case.
10 cm
5 cm
4 cm
8 cm

Answers
Answer:
241.5cm³
Step-by-step explanation:
Volume of the glass = Volume of the cuboid - Volume of the cylinder
Volume of the cuboid = Length * width * height
Volume of the cuboid = 8cm * 4cm * 10cm
Volume of the cuboid = 320cm³
Volume of the cylinder = πr²h
Radius r = 5/2 = 2.5cm
height = 4cm
Volume of the cylinder = 3.14(2.5)²*4
Volume of the cylinder = 78.5cm^3
Volume of the glass = 320 - 78.5
Volume of the glass = 241.5cm³
Examine the following equation.
0=−3x^2+5x+9
Which answer can be used to find the solutions to the equation using the quadratic formula?

Answers
To solve the quadratic function -3x² + 5x + 9 = 0, the formula that should be used is Option C: x = (-5 ± √133) / -6.
What is a quadratic function?
A polynomial function with one or more variables, where the largest exponent of the variable is two, is referred to as a quadratic function. It is also known as the polynomial of degree 2 since the greatest degree term in a quadratic function is of second degree.
The quadratic formula is used to solve quadratic equations in the form of ax² + bx + c = 0, where a, b, and c are constants.
To use the quadratic formula to solve the equation -3x² + 5x + 9 = 0, we need to identify the values of a, b, and c.
In this case, a = -3, b = 5, and c = 9.
Therefore, we can use these values to plug into the quadratic formula -
x = (-b ± √(b² - 4ac)) / 2a
So the answer that can be used to find the solutions to the equation using the quadratic formula is -
x = (-5 ± √(5² - 4 × (-3) × 9)) / 2 × (-3)
Solving this equation we get -
x = (-5 ± √(25 + 108)) / -6
x = (-5 ± √133) / -6
Therefore, the solution is obtained by the equation x = (-5 ± √133) / -6.
To learn more about quadratic function from the given link
https://brainly.com/question/25841119
#SPJ1
PLEASE EXPLAIN!!!
You are planning to use a ceramic tile design in your new bathroom. The tiles are equilateral triangles. You decide to arrange the tiles in a hexagonal shape as shown. If the side of each tile measures 11cm, what will be the exact area of each hexagonal shape?
A: 3,993 cm^2
B: 181.5√3 cm^2
C: 132√3 cm^2
D: 33cm^2
Answers
The exact area of each hexagonal shape is 181.5sqrt(3) cm^2. Option B
To determine the exact area of each hexagonal shape formed by the equilateral triangles, we need to calculate the area of one equilateral triangle and then multiply it by the number of triangles that make up the hexagon.
The formula to calculate the area of an equilateral triangle is:
Area = (sqrt(3) / 4) * side^2
Given that the side of each tile measures 11 cm, we can substitute this value into the formula to find the area of one equilateral triangle:
Area = (sqrt(3) / 4) * (11 cm)^2
= (sqrt(3) / 4) * 121 cm^2
= 121sqrt(3) / 4 cm^2
Now, since the hexagon is formed by six equilateral triangles, we can multiply the area of one triangle by 6 to find the total area of the hexagon:
Hexagon Area = 6 * (121sqrt(3) / 4 cm^2)
= 726sqrt(3) / 4 cm^2
= 181.5sqrt(3) cm^2
Therefore, the exact area of each hexagonal shape is 181.5sqrt(3) cm^2.
The correct answer is B: 181.5√3 cm^2.
For more such questions on hexagonal visit:
https://brainly.com/question/25907410
#SPJ8
Hijk is a rectangle prove diagonals of a rectangle are congruent
Answers
The diagonals of the rectangle are congruent by the rule of side angle side.
What is rectangle?It is defined as the two-dimensional geometry in which the angle between the adjacent sides are 90 degree. It is a type of quadrilateral.
We have a rectangle HIJK
In the triangle HKJ and triangle KHI:
KJ = HI (congruent sides)
Side HK of triangle HKJ = side HK of triangle KHI (common side)
Angle IHK = JKH (right angle)
∴ ΔHKJ ≅ ΔKHI
By SAS rule of congruence.
HJ = Ik
Thus, the diagonals of the rectangle are congruent by the rule of side angle side.
Learn more about the rectangle here:
https://brainly.com/question/15019502
#SPJ4

MA.912.FL.3.2: Solve real-world problems involving simple, compound and continuously compounded interest.
1. Earl opens a certificate of deposit with $1,500 that pays 2.75% compounded daily.
Part A: Write an equation to model this situation.
Part B. How much money will be in the account after 1 year?
Part C. How much money will be in the account after 5 years?
Answers
Part A: The formula for the future value of an investment with compound interest is given by:
A = P(1 + r/n)^(nt)
Where: A = the future value of the investment P = the principal investment amount r = the annual interest rate (as a decimal) n = the number of times the interest is compounded per year t = time in years
For this situation, P = $1,500 r = 2.75% = 0.0275 (since the interest rate is given as an annual rate, we need to divide it by 100 to convert it to a decimal) n = 365 (since interest is compounded daily) t = 1 (since we are looking for the value after one year)
Therefore, the equation to model this situation is:
A = 1500(1 + 0.0275/365)^(365*1)
Part B: To find the value of the account after one year, we can simply substitute t=1 into the equation:
A = 1500(1 + 0.0275/365)^(365*1) = $1,543.21
Therefore, the amount of money in the account after 1 year is $1,543.21.
Part C: To find the value of the account after 5 years, we need to substitute t=5 into the equation:
A = 1500(1 + 0.0275/365)^(365*5) = $1,805.59
Therefore, the amount of money in the account after 5 years is $1,805.59.
Factor
F(x)= x^2 + 2x - 35
Answers
Answer:
Step-by-step explanation:

The area of a trapezoid is $60$. The length of one base is $7$ units greater than the other base, and the height of the trapezoid is $5$. Find the length of the median of the trapezoid.
Answers
Answer:
12
Step-by-step explanation:
you add 5 and 7 for the median
The length of the median of the trapezoid is 12 units if the area of a trapezoid is 60.
What is a trapezoid?It is defined as the quadrilateral having four sides in which two sides are parallel to each other, it is a 2-dimensional geometry.
We have:
The area of a trapezoid is 60.
The length of one base is 7 units greater than the other base, and the height of the trapezoid is 5.
As we know,
The area of the trapezoid:
A =(a+b)h/2
b = a + 7
h = 5
A = 60 units square
Plug the above values in the formula:
60 =(a + a + 7)5/2
120 =(a + a + 7)5
120 =(2a + 7)5
120/5 =(2a + 7)
24 = 2a + 7
2a = 24 - 7
2a = 17
a = 17/2
a = 8.5 units
b = a + 7 = 8.5 + 7 = 15.5
The length of median = (8.5+15.5)/2
The length of the median = 12
Thus, the length of the median of the trapezoid is 12 units if the area of a trapezoid is 60.
Learn more about the trapezoid here:
brainly.com/question/8643562
#SPJ2
If the discriminant, b^2-4ac is ___, a quadratic will have two real roots, two points of intersection with the x-axis.
a) negative
b) positive
c) complex
d) zero
Answers
If the discriminant, b² - 4ac is positive
How to complete the statement?From the question, we have the following equation of discriminant
The discriminant (d) is calculated as
d = b² - 4ac
The solutions of a quadratic equation are dependent on the following conditions
If d = 0, the quadratic equation has 1 real solutionIf d < 0, the quadratic equation has imaginary solutionsIf d > 0, the quadratic equation has 2 different real solutionsThis means that "d > 0, the quadratic equation has 2 different real solutions" implies that the discriminant is positive
Hence, the complete statement is (b) positive
Read more about discriminant at
brainly.com/question/64103
#SPJ1
The height of a trapezoid is 6 in. and its area is 72 inches squared. One base of the trapezoid is 6 inches longer than the other base. What are the LENGTHS of the bases?
Answers
Answer:
9 and 15 inches
Step-by-step explanation:
The unknown lengths can be found by making use of the formula for the area of a trapezoid.
__
Let x represent the shorter base. Then the longer one is (x+6), and the area is ...
A = 1/2(b1 +b2)h . . . . area of a trapezoid with bases b1, b2, and height h
72 = 1/2(x +(x+6))(6)
24 = 2x +6 . . . . . . . . . simplify, divide by 3
18 = 2x . . . . . . . . . subtract 6
9 = x . . . . . . divide by 2
15 = x+6 . . . . . . the length of the longer base
The bases are 9 inches and 15 inches in length.
The piston diameter of a certain hand pump is 0.5inch.The manager determines that the diameters are normally distributed with a mean of 0.5inch and the standard deviation of 0.003inch. After recalibrating the production machine, the manager randomly selects 29 pistonsand determines that the standard deviation has decreased at the a=0.10 level of significance? What are the correct hypotheses for this test? The nut hypothesis is H0? The alternative hypothesis is H1
Answers
The correct hypotheses for this test can be stated as follows:
Null Hypothesis (H0): The standard deviation of the piston diameters is not significantly different after recalibrating the production machine. The standard deviation remains the same or has increased.
Alternative Hypothesis (H1): The standard deviation of the piston diameters has significantly decreased after recalibrating the production machine.
In summary:
H0: σ ≥ σ0 (standard deviation remains the same or has increased)
H1: σ < σ0 (standard deviation has significantly decreased)
Where:
σ is the population standard deviation after recalibration
σ0 is the population standard deviation before recalibration
To know more about hypotheses refer here:
https://brainly.com/question/18064632#
#SPJ11
What is the equation of the line that passes through the point (-6,4) and has a
slope of o?
Answers
Answer:
\(y=0x+4\)
Step-by-step explanation:
Given the following question:
Point A = (-6, 4) = (x, y)
Slope = 0
To find the equation of the line we are going to use the slope intercept form y = mx + b, substitute the values in for the variables and then solve for b to have our answer.
\(y=mx+b\)
\(y=4\)
\(m=0\)
\(x=-6\)
\(4=0(-6)+b\)
\(0\times-6=0\)
\(4=0+b\)
\(4+0=4\)
\(4=b\)
\(b=4\)
\(y=0x+4\)
The equation of the line is "y = 0x + 4."
Hope this helps.
Answer:
y = 4
Step-by-step explanation:
Given :-
passes through the point (-6, 4)slope = 0To Find :-
equation of lineSlope :-
We know coordinates of y-intercept are : (0, b)Using point-slope form,b - 4 = 0(0 + 6)b - 4 = 0b = 4Substitution
Using the slope-intercept form,y = mx + by = 0x + 4y = 4