math help pls
3x+4(x-8)-x=3/5(10x+15)
Answers

Related Questions
The ratio of C:D is 5:3, the ratio of F:D is 6:1.
Find the ratio of C:D:F.
Answers
The ratio of C:D:F is 5:3:18.
What is ratio?The ratio is defined as the comparison of two quantities of the same units that indicates how much of one quantity is present in the other quantity.
here, we have,
given that,
The ratio of C:D is 5:3,
the ratio of F:D is 6:1.
i.e. F:D= 18:3
now,
C:D:F= 5:3:18.
To learn more on ratio click:
brainly.com/question/13419413
#SPJ1
Given the quadratic equation x^(2)+4x+c=0, what must the value of c be in order for the equation to have solutions at x=-3 and x=-1 ?
Answers
Answer:
Step-by-step explanation:
If the solutions are x = -3 and x = -1, then (x - 3) (x - 1) will give us our answer. Using the FOIL method,
(x - 3) (x - 1)
x^2 - x - 3x + 3
x^3 - 4x + 3 = 0
Your answer is 3
A spring has a natural length of 30.0 cm. If a 20.0-N force is required to keep it stretched to a length of 42.0 cm, how much work W is required to stretch it from 30.0 cm to 36.0 cm? (Round your answer to three decimal places.) W = ______ J
Answers
The amount of work required to stretch the spring from 30.0 cm to 36.0 cm is 1.411 joules, which can be rounded to three decimal places.
According to Hooke's Law, the amount of work required to stretch or compress a spring by a certain amount is given by the formula:
W = (1/2) k (x2 - x1)²
where W is the work done (in joules), k is the spring constant (in newtons per meter), x1 is the initial displacement (in meters), and x2 is the final displacement (in meters).
In this case, the spring has a natural length of 30.0 cm, which is equivalent to 0.3 meters. To find the spring constant, we can use the fact that a 20.0-N force is required to keep it stretched to a length of 42.0 cm, which is equivalent to 0.42 meters.
Using Hooke's Law, we have
F = k (x2 - x1)20.0 N
= k (0.42 - 0.3) m
=> k = 80.0 N/m
Now we can use Hooke's Law again to find the amount of work required to stretch the spring from 30.0 cm to 36.0 cm, which is equivalent to 0.36 meters.
Using Hooke's Law, we have:
F = k (x2 - x1)W
= (1/2) k (x2 - x1)²W
= (1/2) (80.0 N/m) (0.36 - 0.3) m²W
= 1.411 J
You can learn more about Hooke's Law at: brainly.com/question/29126957
#SPJ11
In the diagram, what is the ratio of patterned circles to plain circles?
Four arrays of circles are represented. First array has a plain circle. Second array has 4 patterned circles and 1 plain circle. Third array has 1 patterned circle and 4 plain circles. Fourth array has a plain circle.

Answers
The ratio of the patterned circles to plain circles is 6 : 7.
We are given the four arrays of the circles.
In the first array, we have only 1 plain circle.
In the second array, we have 4 patterned circles and 1 plain circle.
In the third array, we have 1 patterned circle and 4 plain circles.
In the fourth array, we have only 1 plain circle.
So, total patterned circles = 5 + 1
Total patterned circles = 6
Total plain circles = 1 + 1 + 4 + 1
Total plain circles = 7
Ratio of patterned circles to plain circles will be given as:
6 : 7
Therefore, we get that, ratio of the patterned circles to plain circles is 6 : 7.
Learn more about ratio here:
https://brainly.com/question/2328454
#SPJ9
Kara and her friends have $17 to spend at a pizza parlor.they would like to buy large pizza which costs $12 and then add as many toppings as possible if each topping (t) cost 50cents,which inequality describes the maximum number of toppings that the group can purchase?
Answers
Answer:kara Had $17-$12. Pizza cost =leave u with $5 x.50=10topping
Step-by-step explanation:
The volume of a rectangular prism is the product of its length, width, and height. The length of a rectangle prism is 3 feet more than five times its height. The width is 5 feet less than six times its height. Express the length and width in terms of the height h. The length is The width is (Be sure to Write down the expanded form of the expression for the volume: expand the volume expression) (Express the interval in which the In what range must the height fall? He height must be)
Answers
The length and width in terms of the height h is 5h+3 feet and 6h-5 feet respectively, the volume will be \(30h^3 - 7h^2 -15h\) units and the height must be in the interval of \([0,\infty)\).
According to the question,
The height of the rectangular prism is h.
The length of the rectangular prism is 5h+3 feet
The width of the rectangular prism is 6h-5 feet
The volume of the rectangular prism can be calculated as:
\(Length \times width \times height = Volume\)
Substitute the value of height, length and width in the formula:
\(V = (5h+3) \times (6h-5) \times h\)
V = \((30 h^2 -7h-15)h\)
\(V = 30h^3 - 7h^2 -15h\)
The height is always positive. So, the interval in which the In what range must the height fall is \([0,\infty)\).
The length and width in terms of the height h is 5h+3 feet and 6h-5 feet respectively and the volume will be \(30h^3 - 7h^2 -15h\) units
The height must be in the interval of \([0,\infty)\).
Learn more about rectangular prism here:
https://brainly.com/question/29124743
#SPJ12
Stacia needs enough ribbon to wrap around the length (ℓ) and height (h) of a box. If the length is 2 feet and the height is 4 inches, how much ribbon will she need? If ribbon is sold in whole number yards and costs $1.50 per yard, how much will it cost Stacia to buy the ribbon?
Answers
To wrap around the length and height of a box with a length of 2 feet and a height of 4 inches, Stacia needs 56 inches of ribbon. Stacia needs to buy 2 yards of ribbon at a cost of $3.00.
To calculate the amount of ribbon needed to wrap around the length and height of a box, we need to find the perimeter of the box. The perimeter is the sum of the lengths of all the sides of the box.
In this case, the box has a length of 2 feet, which is equivalent to 24 inches (since 1 foot = 12 inches), and a height of 4 inches. To calculate the perimeter, we need to add up the length and height of the box, and then multiply by 2:
Perimeter = 2 * (length + height)
Perimeter = 2 * (24 + 4)
Perimeter = 56 inches
Therefore, Stacia needs 56 inches of ribbon to wrap around the length and height of the box.
To convert inches to yards, we divide by 36 (since 1 yard = 36 inches):
56 / 36 = 1.56 yards
Since ribbon is sold in whole number yards, Stacia will need to buy 2 yards of ribbon.
The cost of the ribbon will be:
2 * $1.50 = $3.00
Therefore, it will cost Stacia $3.00 to buy the ribbon.
To learn more about perimeter please click on below link
https://brainly.com/question/6465134
#SPJ1
The life expectancy of Timely brand watches is normally distributed with a mean of four years and a standard deviation of eight months.
a. What is the probability that a randomly selected watch will be in working condition for more than five years?
b. The company has a three year warranty period on their watches. What percentage of their watches will be in operating condition after the warranty period?
c. What is the minimum and the maximum life expectancy of the middle 95% of the watches?
d. Ninety-five percent of the watches will have a life expectancy of at least how many months?
Answers
a.The probability that a randomly selected watch will be in working condition for more than five years is approximately 6.68%. b.Approximately 93.32% of the watches will be in operating condition after the warranty period. c. The maximum life expectancy of the middle 95% of the watches is approxiamately 63.68 months. d.The range of the middle 95% of the watches is from 32.32 months to 63.68 months. The range represents 95% of the watches, it means that 5%.
a. To find the probability that a randomly selected watch will be in working condition for more than five years, we need to convert the time to the same unit as the distribution. Since the mean is given in years and the standard deviation is given in months,
we need to convert five years to months.
Mean = 4 years = 4 x 12 months = 48 months
Standard deviation = 8 months
To calculate the probability, we need to find the area under the normal distribution curve to the right of 60 months (5 years).
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to 60 months:
z = (x - μ) / σ
z = (60 - 48) / 8 = 12 / 8 = 1.5
The probability can be found by looking up the z-score in the standard normal distribution table or using a calculator. From the table or calculator, we find that the probability is approximately 0.0668, or 6.68%.
b. The warranty period for Timely brand watches is three years. To find the percentage of watches that will be in operating condition after the warranty period, we need to find the probability that a randomly selected watch will last longer than three years.
We need to convert three years to months:
Warranty period = 3 years = 3 x 12 months = 36 months
We calculate the z-score:
z = (x - μ) / σ
z = (36 - 48) / 8 = -12 / 8 = -1.5
Using the standard normal distribution table or a calculator, we find the area to the left of -1.5 is approximately 0.0668. The probability that a randomly selected watch will not last longer than three years is approximately 0.0668.
To find the percentage of watches that will be in operating condition after the warranty period, we subtract this probability from 1 (since we want the complementary probability):
Percentage = 1 - 0.0668 = 0.9332 = 93.32%
c. The middle 95% of the watches represents the range within which 95% of the watches' life expectancy falls. To find the minimum and maximum life expectancy of this range, we need to determine the z-scores that correspond to the cumulative probability of 0.025 and 0.975.
For the minimum life expectancy (lower bound), we look up the z-score that corresponds to a cumulative probability of 0.025. This z-score is approximately -1.96.
z = -1.96
Using the z-score formula, we can find the corresponding value in months:
x = μ + (z x σ)
x = 48 + (-1.96 * 8) = 48 - 15.68 = 32.32
The minimum life expectancy of the middle 95% of the watches is approximately 32.32 months.
For the maximum life expectancy (upper bound), we look up the z-score that corresponds to a cumulative probability of 0.975. This z-score is also approximately 1.96.
z = 1.96
Using the z-score formula, we can find the corresponding value in months:
x = μ + (z x σ)
x = 48 + (1.96 x 8) = 48 + 15.68 = 63.68
d. Ninety-five percent of the watches refer to the range between the 2.5th and 97.5th percentiles. We already calculated the z-scores corresponding to these percentiles in part c: -1.96 and 1.96.
To find the range in months,
we convert the z-scores back:
\(x_{1}\)= μ +\(z_{1}\) x σ = 48 + (-1.96) x 8 = 32.32 months,
and \(x_{2}\)= μ + \(z_{2}\) x σ
= 48 + 1.96 x 8
= 63.68 months.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ4
Write the number for eight thousand seven hundred ninety-nine.
Answers
Answer:
The number says eight thousand so you take eight thousand and 7 hundred 99 so that would be 8,799
write the birds an order from shortest egg to longest egg
canda goose 3 2/5 Robin 3/4 turtle dove 1 1/5 raven 1 1/9
Answers
Answer:
roben,dove,raven ,goose
Step-by-step explaunation:
you need to change them to the same denominator *first*
Answer:
Robin, Raven, Turtle dove, Canada goose.
Step-by-step explanation:
We are given the size of the eggs.
Canada goose: 3 2/5 Units = 17/5 UnitsRobin: 3/4 UnitsTurtle dove: 1 1/5 Units = 6/5 UnitsRaven: 1 1/9 Units = 10/9 UnitsNow, we need to put the sizes of eggs in ascending order.
=> \(\frac{17}{5},\frac{3}{4} ,\frac{6}{5} , \frac{10}{9}\)
Step 1: Make the denominators same.
=> \(\frac{17}{5},\frac{3}{4} ,\frac{6}{5} , \frac{10}{9}\)
=> \(\frac{612}{180} ,\frac{135}{180} ,\frac{216}{180}, \frac{200}{180}\)
Step 2: Order these egg sizes in ascending order.
=> \(\frac{612}{180} ,\frac{135}{180} ,\frac{216}{180}, \frac{200}{180}\)
=> \(\frac{135}{180},\frac{200}{180},\frac{216}{180},\frac{612}{180}\)
Step 3: Match the sizes of the eggs with the bird.
Robin, Raven, Turtle dove, Canada goose.
Final Answer: So, after working on this problem, we can conclude that the ascending order of bird's eggs size is:
Robin, Raven, Turtle dove, Canada goose.
Hoped this helped.
Solve the system by graphing, then state the solution as an ordered pair
HELP ASAP!!!!!

Answers
Step-by-step explanation:
Simply graph the two equations....the intersection of the two graphs is the solution

Drag the expressions to the correct functions. Not all expressions will be used.
Consider the functions fand g.
= 4x² + 1
g(x) =
Perform the function compositions:
x² - 3
Answers
The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)).
Let the functions be f(x) = 4x² + 1 and g(x) = x² - 3
The correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
What is composition function?The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)). In this operation, the function g exists used for the outcome of applying the function f to x.
Given:
f(x) = 4x² + 1 and g(x) = x² - 3
a) (f o g)(x) = f[g(x)]
f[g(x)] = 4(x² - 3)² + 1
substitute the value of g(x) in the above equation, and we get
= 4(x⁴ - 24x + 9) + 1
simplifying the above equation
= 4x⁴ - 96x + 36 + 1
= 4x⁴ - 96x + 37
(f o g)(x) = 4x⁴ - 96x + 37
b) (g o f)(x) = g[f(x)]
substitute the value of g(x) in the above equation, and we get
g[f(x)] = (4x² + 1)²- 3
= 16x⁴ + 8x² + 1 - 3
simplifying the above equation
= 16x⁴ + 8x² - 2
(g o f)(x) = 16x⁴ + 8x² - 2.
Therefore, the correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
To learn more about the function refer to:
https://brainly.com/question/26709985
#SPJ9
Given the LP model below. Do the following: a. Formulate the new LP model. b. Set up the initial table then identify the optimum column, pivotal row, entering variable out, going variable, Zj row entries, and Cjn - Zj row entries Maximize eamings =$0.80X 1
+$0.40X 2
+$1.20X 3
−$0.10x 4
subject to X 1
+2X 2
+X 3
+5X 4
≤150 X 2
−4X 3
+8X 4
=70 6X 1
+7X 2
+2X 3
−X 4
≥120 X 1
,X 2
,X 3
,X 4
≥0
Answers
(a) The new LP model is formulated by converting the given LP model into standard form by introducing slack, surplus, and artificial variables as necessary.
(b) To set up the initial table and identify the optimum column, pivotal row, entering variable out, going variable, Zj row entries, and Cjn - Zj row entries, the LP model needs to be solved using the simplex method step by step.
(a) To formulate the new LP model, we need to convert the given LP model into standard form by introducing slack, surplus, and artificial variables. The slack variables are added to the inequality constraints, surplus variables are added to the equality constraints, and artificial variables are added to represent any negative right-hand side values. The objective function remains the same. The new LP model is then ready to be solved using the simplex algorithm.
(b) Setting up the initial table involves converting the new LP model into a tableau form. The initial tableau consists of the coefficient matrix, the right-hand side values, the objective function coefficients, and the artificial variables. The simplex algorithm is applied iteratively to identify the optimum column (the most negative coefficient in the objective row), the pivotal row (determined by the minimum ratio test), the entering variable (corresponding to the minimum ratio in the pivotal column), and the outgoing variable (the variable exiting the basis).
During each iteration, the Zj row entries are calculated by multiplying the corresponding column of the coefficient matrix with the basic variable's coefficients. The Cjn - Zj row entries are obtained by subtracting the Zj row entries from the objective function coefficients. The process continues until an optimal solution is reached, where all the coefficients in the objective row are non-negative.
By following these steps and performing the simplex algorithm iterations, the optimum column, pivotal row, entering variable out, going variable, Zj row entries, and Cjn - Zj row entries can be identified to determine the optimal solution of the LP model.
LEARN MORE ABOUT LP model HERE:
https://brainly.com/question/33013045
#SPJ11
write an equation in slope intercept form of the line that passes through the given point and is parallel to the graph of the given equation. (-7,-5);y= -4x+5)
Answers
Answer:
y=-4x-33
Step-by-step explanation:
Since the equation is parallel it will have the same slope which is -4
Now just plug in the points into the equation y=-4x+n
Plug them in and you get -5=-4(-7)+n
Then solve which will get you n=-33
Therefore the equation is y=-4x-33
What is one geometrical fact explained in the lecture that reflects the mathematical technique da Vinci used in The Last Supper? a. He doesn?t use mathematics in the painting. B. He uses trigonometry to find the exact place where each thing should be located and create the picture plane. C. He uses the coffers of the ceiling to place Jesus in the mathematical center, and to create an illusion that extends the room beyond what is visible.
Answers
Answer:
C. He uses the coffers of the ceiling to place Jesus in the mathematical center, and to create an illusion that extends the room beyond what is visible.
Step-by-step explanation:
See attached. We can see that this option is the best as it reflects what we can see in the painting.
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather

Answer:
c
Step-by-step explanation:
IM GIVING BRAINLIEST!! I PROMISE!!PLEASE HELP!!!
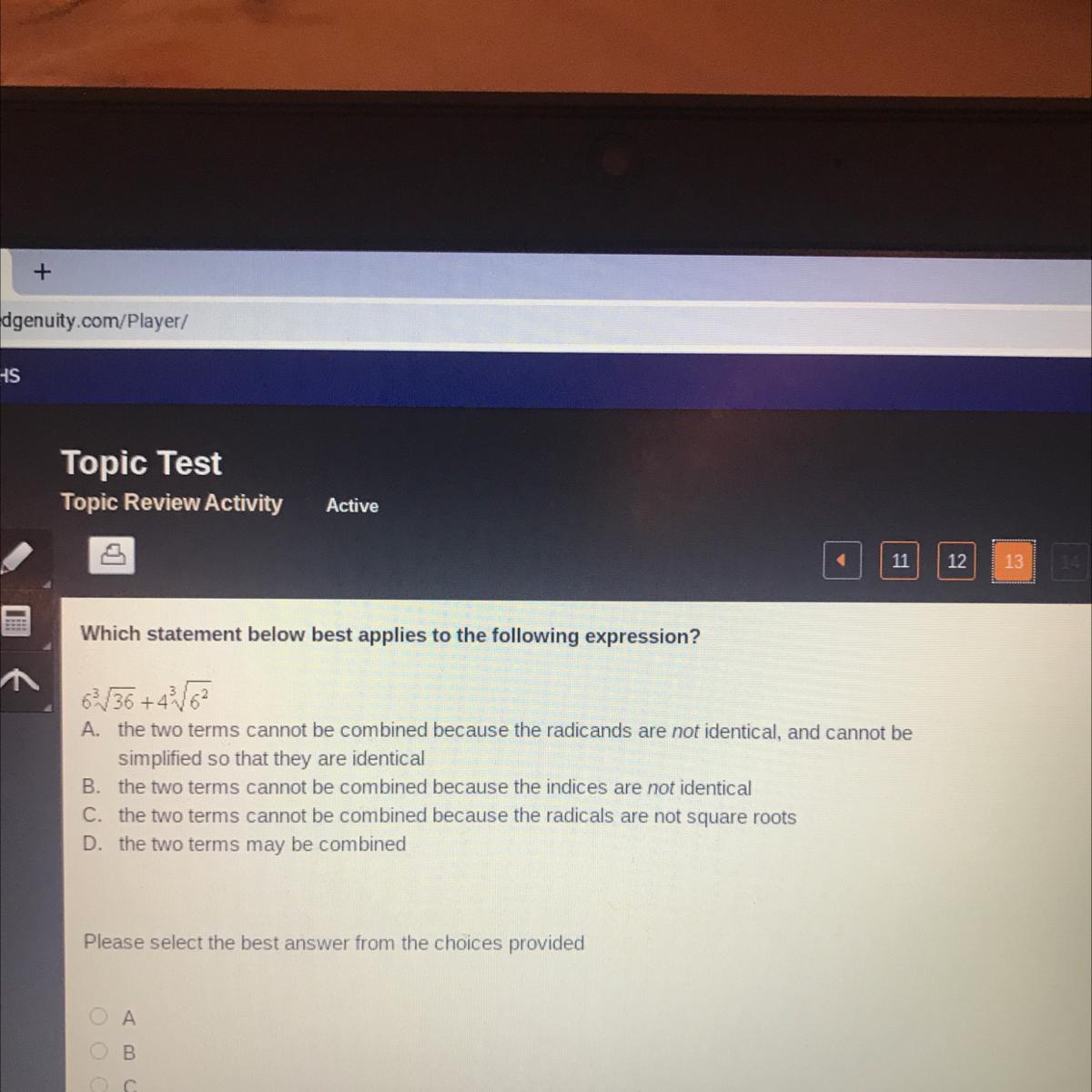
Answers
Answer:
B
Step-by-step explanation:
brainliest please?
A ______________ consists of a limited number of people from the overall population, selected in such a way that each has an equal chance of being chosen.
Answers
A random sample is a representative subset of individuals selected from the larger population in such a way that each member of the population has an equal chance of being chosen.
The purpose of a random sample is to obtain a sample that is unbiased and reflects the characteristics of the entire population.
By giving every individual an equal opportunity to be included in the sample, random sampling helps minimize selection bias and ensures that the sample is more likely to be representative of the population as a whole. This allows researchers to make valid inferences and generalizations about the population based on the characteristics observed in the random sample.
Random sampling is widely used in various fields, including research, surveys, and statistical analysis, to draw reliable conclusions about a larger population based on a smaller subset of individuals.
Learn more about statistical here:
https://brainly.com/question/32201536
#SPJ11
let f(t)f(t) be the number of us billionaires in year tt. in 1985 there were 13 us billionaires, and in 1990 there were 99 us billionaires. assuming the yearly increase remains constant, find a formula predicting the number of us billionaires in year tt.
Answers
The formula predicting the number of US billionaires in any given year (t) is:f(t) = 17.2t - 34,129. We can assume a linear growth model on the based of given information.
The given data states that in the year 1985, there were 13 US billionaires. Whereas in 1990, there were 99 US billionaires. We have to find out the formula that predicts the number of US billionaires in any given year (t).
The yearly increase remains constant, so we can consider the formula for the linear function.f(t) = mt + b
where
t is the year and f(t) is the number of US billionaires in that year (t).
m is the slope of the line and b is the y-intercept.
The slope of the line is given by the formula:m = (y₂ - y₁) / (x₂ - x₁)
Let's plug in the given values to find the slope of the line.m = (99 - 13) / (1990 - 1985)m = 86 / 5m = 17.2 .The y-intercept of the line can be found by substituting the values of t and f(t) from any of the given points into the equation of the line.
Let's use the point (1985, 13).f(t) = mt + b => f(1985) =17.2(1985) + b => f(1985) = 34,142 + b =>b = 13 - 34,142 & b = -34,129.
The formula predicting the number of US billionaires in any given year (t) is:f(t) = 17.2t - 34,129
To know more about linear growth model refer here:
https://brainly.com/question/28033207
#SPJ11
Divide.
(−1/6)÷(−5/6)
What is the quotient?
Enter your answer as a simplified fraction in the box. please thank you!!!
Answers
Answer:
(−1/6)÷(−5/6) which when you cancel gets 0.2 or also 1/5.
Step-by-step explanation:
|x + 5| – |2w| When x = 2 and w = –4
Answers
(2 + 5) - (2 x -4) = 15
7 - -8
Minus a negative goes upwards.
15
Answer:
-1
Step-by-step explanation:
lx+5l -- l2wl
l2+5l -- l2x-4l
7 -- l2x-4l
7 -- 8
-1
Brenda has 14 fewer apps than Caleb. If Caleb deleted 5 apps, then he would have twice as many as Brenda. How many apps do Brenda and
Caleb have together?

Answers
Answer:
42
Step-by-step explanation:
Because Brenda has 14 fewer apps and he deleted 5 apps and he now has twice as many as brenda so 14 + 14 =28 so he had 33 before but remember 33- 5 + 28 so 14 + 28 + 42
Let U=(1, 2, 3, 4, 5, 6, 7, 8), A={1, 2, 3, 6), and B=(3, 4, 5). Find the set An B. ANB=
Answers
The set A ∩ B = {3}
The intersection of sets, denoted as A ∩ B, refers to the set that contains elements that are common to both sets A and B. In this case, set A consists of the elements {1, 2, 3, 6}, and set B consists of the elements {3, 4, 5}.
The intersection of A and B, written as A ∩ B, represents the set of elements that appear in both sets simultaneously.
To find the intersection of sets A and B, we examine each element of set A and check if it is also present in set B. In this case, the element 3 is the only element that exists in both sets.
Therefore, the intersection of sets A and B is {3}.
Learn more about intersection
brainly.com/question/12089275
#SPJ11
Karen and $41 each week working part time at a at a bookstore she earns one additional dollar for each book that she sells AB the amount in Dallas accurate as in a week if she sells books right the equation relating a to B then use the equation to find the amount of money Karen and if she sells recent books
Answers
The value of amount Kala earns if she sells 14 books is, 55 dollars
What is Addition?The process or combination of combining two or more numbers is called the Addition.
Given that;
Karen and $41 each week working part time at a at a bookstore.
Hence, We get;
The Equation is,
A = 41 + B
And, B = 14
Hence, We get;
A = 41 + 14
A = 55
Thus, The value of amount Kala earns if she sells 14 books is,
⇒ 55 dollars
Learn more about the addition visit:
https://brainly.com/question/25421984
#SPJ1
Complete question is this;
Kala earns 41 dollars each week working part-time at a bookstore. She earns one additional dollar for each book that she sells.
Let A be the amount (in dollars) that Kala earns in a week if she sells B books.
Write an equation relating A to B. Then use this equation to find the amount of money Kala earns if she sells 14 books.
Equation:
Amount Kala earns if she sells 14 books: dollars
Two trains leave stations 432 miles apart at the same time and travel toward each other. One train travels at 80 miles per hour while the other travels at 100 miles per hour. How long will it take for the two trains to meet?
Answers
Answer:
The trains will meet in 2.4 hours.
Step-by-step explanation:
To cover 432 miles at 180mph:
432mi/180mph=2.4 hours
Write an equation in slope-intercept form for the line.
(-7,2) and (5,8)
Answers
The equation in slope-intercept form for the line that passes from the points (-7,2) and (5,8) is y = (1/2)x -3/2.
We know that, the slope intercept form is given by:-
y = mx + b
Where,
(x,y) is the ordered pair of every point on the line
m is the slope of the line
b is the y-intercept of the line
We know that, slope = (8-2)/(5-(-7)) = 6/12 = 1/2
Putting (-7,2) in (x,y) and m = 1/2 in the slope intercept form, we get,
2 = (1/2)(-7) + b
2 = -7/2 + b
b = -3/2
Hence, the slope intercept form of the line is y = (1/2)x -3/2.
To learn more about slope-intercept form, here:-
https://brainly.com/question/9682526
#SPJ4
The functions u and w are defined as followu(x)=x-1W(x) = -p²-2Find the value of w(u(-1)).

Answers
Given:
\(\begin{gathered} u(x)=x-1 \\ \\ w(x)=-x^2-2 \end{gathered}\)Let's find the value w(u(-1)).
Let's find w(u(x)).
We have:
\(w(u(x))=-(x-1)^2-2\)Thus, to find w(u(-1)), substitute -1 for x in the equation above:
\(\begin{gathered} w(u(-1))=-(-1-1)^2-2 \\ \\ w(u(-1))=-(-2)^2-2 \\ \\ w(u(-1))=-4-2 \\ \\ w(u(-1))=-6 \end{gathered}\)ANSWER:
w(u(-1)) = -6
3x^2 - 11x +6
Factor using any method. Show your work in the box. Explain how you accounted for the non-zero leading coefficient (the 3 in front) when factoring.
Answers
Answer: The factored form of 3x^2 - 11x + 6 is (x - 3)(3x - 2).
Step-by-step explanation: To factor the quadratic expression 3x^2 - 11x + 6, we can use the method of factoring by grouping. Here's how it's done:
Multiply the coefficient of the quadratic term (3) by the constant term (6): 3 * 6 = 18.
Find two numbers that multiply to 18 and add up to the coefficient of the linear term (-11). In this case, the numbers are -2 and -9 (-2 * -9 = 18 and -2 + -9 = -11).
Split the linear term -11x into -2x - 9x. Rewrite the original expression using these terms:
3x^2 - 2x - 9x + 6.
Group the terms and factor by grouping:
(3x^2 - 2x) + (-9x + 6).
Factor out the greatest common factor from each group:
x(3x - 2) - 3(3x - 2).
Notice that (3x - 2) is a common factor. Factor it out:
(x - 3)(3x - 2).
Therefore, the factored form of 3x^2 - 11x + 6 is (x - 3)(3x - 2).
For more questions on factored form
https://brainly.com/question/24024818
#SPJ11
How do you find the area of the base and volume and height
I5 in
13 in

Answers
Volume of the pyramid is 4390.74 and base area is 439.07 cubic inches.
The given figure is a hexagonal pyramid.
The base of the pyramid is hexagon.
We have to find the base of the pyramid by formula :
Base area = 3√3/2a²
Where a is the base length.
Base area = 3√3/2(13)²
= 3√3/2 ×169
=439.07 square inches.
Volume =√3/2b²h
h is height which is 30 in and b is base length of 13 in.
Volume =√3/2×169×30
=√3/2×5070
=2535×√3
=4390.74 cubic inches.
Hence, volume of the pyramid is 4390.74 and base area is 439.07 cubic inches.
To learn more on Volume click:
https://brainly.com/question/13798973
#SPJ1
I don't know how to do this one

Answers
Answer:
Each side is 1/13 miles long
Step-by-step explanation:
The area of a square is A=s^2 where s is the side length of the square. Remember that a square has all of its sides equal in length to each other. So since we already have the area which is A=1/169mi^2, then we just take the square root of it to get s=1/13. So each side will be 1/13 miles long
add or subtract the polynomials
(8x3+3x-2)+(9x2-7+3x-2x3)
Answers
Answer:
10x^3+9x^2-9
Step-by-step explanation:
8x^3+2x-2+9x^2-7+2x-2x^3 - Combine like terms
10x^3+9x^2-9
Answer:
\(\boxed{\boxed{\sf 6x^3+9x^2+6x-9}}\)
Step-by-step explanation:
\(\sf \left(8x^3+3x-2\right)+\left(9x^2-7+3x-2x^3\right)\)
\(\sf 8x^3+3x-2+9x^2-7+3x-2x^3\)
Note: If there is a negative sign in front of parentheses, each term within the expression changes sign.
\(\Longrightarrow \sf 8x^3+3x-2+9x^2-7+3x-2x^3\)
Now, we need to organize expression into groups like terms:
\(\Longrightarrow \sf (8x^3, -2x^3)\: (3x, 3x)\:(-2,-7)\)
\(\longmapsto\sf 8x^3-2x^3=6x^3\)
\(\longmapsto\sf 3x+3x=6x\)
\(\longmapsto\sf -2-7=-9\)
\(\boxed{\sf 6x^3+9x^2+6x-9}\)
_____________________________