Measure the length of each leg and the hypotenuse.
m∠ABC = 45° m∠ACB = 45°
Question:
AB =? Units
AC =? Units
BC =? Units
Answers
The hypotenuse, AC, is equal to the length of a leg multiplied by √2. , AC = x√2 units.
To summarize:
AB = BC = x units
AC = x√2 units
In a right triangle where one angle is 45°, we can determine the lengths of the legs and the hypotenuse using the properties of a 45-45-90 triangle.
In a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of a leg multiplied by √2.
Let's assume the length of one leg is "x" units.
Since m∠ABC = 45° and m∠ACB = 45°, we can conclude that AB and BC are congruent. So, AB = BC = x units.
The hypotenuse, AC, is equal to the length of a leg multiplied by √2. Therefore, AC = x√2 units.
To summarize:
AB = BC = x units
AC = x√2 units
For such more questions on Legs and Hypotenuse Lengths
https://brainly.com/question/29258809
#SPJ8
Related Questions
I NEED HELP ASAP! The average high temperatures in degrees for a city are listed.
58, 61, 71, 77, 91, 100, 105, 102, 95, 82, 66, 57
If a value of 71° is changed to 93°, which of the following measures changes the most and what is the new value?
Mean 82.3°
Median 86.5°
Range 48°
IQR 34°
Answers
Answer:
The new value of the list after changing 71° to 93° would be:
58, 61, 93, 77, 91, 100, 105, 102, 95, 82, 66, 57
The measure that changes the most would be the median. Without the change, the median was 86.5°, which was the average of the 7th and 8th values in the list (100 + 77) / 2. However, after changing 71° to 93°, the median becomes 91°, which is the average of the 6th and 7th values in the list (91 + 91) / 2.
Therefore, the median has changed by 4.5° (from 86.5° to 91°).
Someone pls help me with both :(

Answers
Answer:
5) A
6) D
Step-by-step explanation:
for 5) I did just looked up online
2.5% of 25,000
and I added it to 25,000
which was 26,265.625
so I looked up 2.5% of 26,265.625 and I kept doing it until the 5th year and I got estimated $28,285.21
for 6) I did similar to 5) but I used the numbers that were given
I looked up 4% of 1,250 and I did that twice and got $1,352.55
hope that helped ;)
Vail Ski Shop received a $1,205 invoice dated July 12 with 2/10, 1/15, n/60 terms. On July 26, Vail sent a $489 partial payment.
a. What credit should Vail receive?
b.What is Vail's outstanding balance
Answers
Outstanding balance = Invoice amount - CreditInvoice amount = $1,205Credit = $611.25Outstanding balance = $1,205 - $611.25Outstanding balance = $593.75Therefore, Vail's outstanding balance is $593.75.
a. To determine the credit that Vail should receive, we need to use the formula for partial payment: Payment / (1 - Discount%)The calculation for the credit that Vail should receive is:Discount% = 2/10 = 0.2Credit = 489 / (1 - 0.2)Credit = 489 / 0.8Credit = $611.25The credit that Vail should receive is $611.25.b.
To calculate Vail's outstanding balance, we need to subtract the credit from the invoice amount. The calculation is:Outstanding balance = Invoice amount - CreditInvoice amount = $1,205Credit = $611.25Outstanding balance = $1,205 - $611.25Outstanding balance = $593.75Therefore, Vail's outstanding balance is $593.75.
Learn more about Invoice here,
https://brainly.com/question/29032299
#SPJ11
A
Samuel's specialty is fences. He has a standard fence he likes to build. It's
perimeter is 76 2/3 feet. If Samuel builds eight of these fences, how many feet of
material will he need? Explain how you found your answer.
Answers
Answer:
Samuel will need 614 2/3 feet of material to build eight of his standard fences. To find this answer, we simply need to multiply 76 2/3 feet (the perimeter of one fence) by 8 (the number of fences he wants to build). Thus, 76 2/3 feet x 8 = 614 2/3 feet.
A spinner with three equal size sections labeled red, green, and yellow is
spun once. Then a coin is tossed, and one of two cards labeled with a 1 or
a 2 is selected. What is the probability of spinning yellow, tossing heads,
and selecting the number 2?
Answers
The probability of spinning yellow, tossing heads, and selecting the number 2 is approximately 0.083325 or 8.33%.
To find the probability of spinning yellow, tossing heads, and selecting the number 2, we need to calculate the individual probabilities of each event and then multiply them together.
Given:
Spinner with three equal size sections (red, green, yellow)
Coin toss with two outcomes (heads, tails)
Two cards labeled with 1 and 2
Firstly calculate the probability of spinning yellow:
Since the spinner has three equal size sections, the probability of spinning yellow is 1/3 or 0.3333.
Secondly calculate the probability of tossing heads:
Since the coin has two possible outcomes, the probability of tossing heads is 1/2 or 0.5.
Thirdly calculate the probability of selecting the number 2:
Since there are two cards labeled with 1 and 2, the probability of selecting the number 2 is 1/2 or 0.5.
Lastly multiply the probabilities together:
To find the probability of all three events occurring, we multiply the individual probabilities:
Probability = (Probability of spinning yellow) * (Probability of tossing heads) * (Probability of selecting the number 2)
Probability = 0.3333 * 0.5 * 0.5
Probability = 0.083325
Therefore, the probability of spinning yellow, tossing heads, and selecting the number 2 is approximately 0.083325 or 8.33%.
To study more about Probability:
https://brainly.com/question/13604758
https://brainly.com/question/24756209
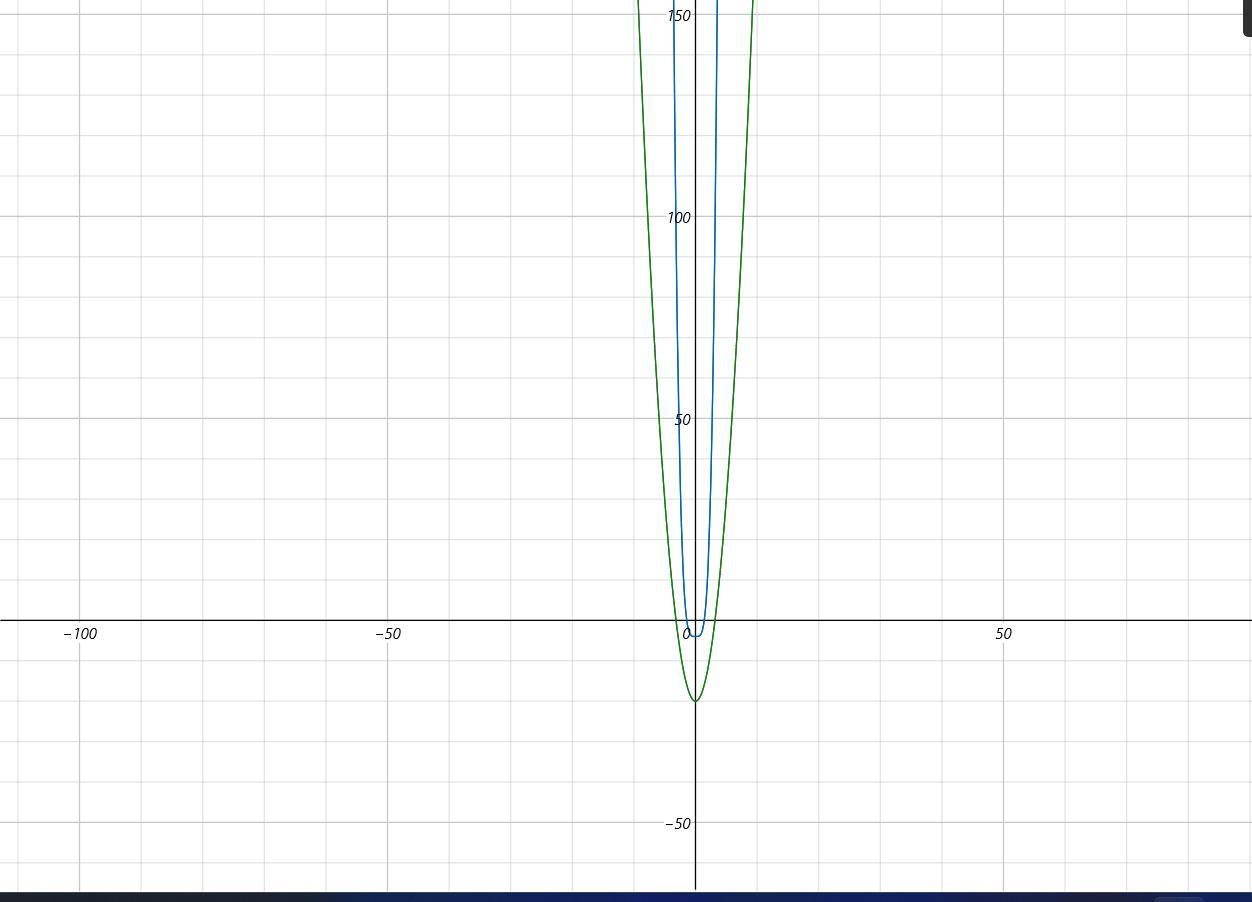
which of the following is the equation of the quadratic function below?

Answers
Answer:
A. y = x² - 9x + 18
Step-by-step explanation:
The key thing to look for in this graph is the y-intercept (where the graph will hit the y-axis).
We can't see exactly where y-intercept is, but we know it is a positive number.
In a standard form quadratic equation:
y = ax² + bx + c
'c' tells you what the y-intercept is.
The choices with positive y-intercept are A and B.
Again, we can't see exactly where y-intercept is, but we know it is not 1.
y = x² - 9x + 18
has a positive y-intercept that is not 1,
thus the answer is A.
f(x)=−2(x+4)
What is the value of f(−1)?
Answers
(-1,-6)
all you have to do it plug in -1 for x
f(-1)= -2(-1+4
f(-1)=-2(3)
f(-1)=-6
!!!!!!!!
Which expression represents the phrase "the quotient of 9 and 14"?

Answers
Answer:
the quotient of 9 and 14
= \(\frac{9}{14}\)
Answer:
the answer is 9 upon 14 (⁹/14)
a player pays $5 to play a game. a die is rolled. if the number on the die is odd,the game is lost. if the number on the die is even, the die is rolled again. in this casethe player wins if the second number matches the first and loses otherwise. how muchshould the player win if the game is fair? (
Answers
The game to be fair, the player should win 60.
In order to determine the fair winnings for this game, we need to calculate the probability of winning and then set it equal to the cost of playing the game.
Step 1: Calculate the probability of winning.
There are two scenarios for winning:
1. First roll is even, and the second roll matches the first.
2. The probability of rolling an even number on a six-sided die is 3/6 or 1/2, since there are three even numbers (2, 4, and 6).
Step 2: Calculate the probability of the second roll matching the first roll.
Since there are 6 sides to the die, the probability of the second roll matching the first is 1/6.
Step 3: Calculate the combined probability of both events.
To find the combined probability of both events, multiply the probabilities: (1/2) × (1/6) = 1/12. So the probability of winning is 1/12.
Step 4: Set up an equation to determine fair winnings.
Let x be the fair winnings for the game. The cost of playing the game is $5. In order for the game to be fair, the expected value (probability of winning multiplied by the winnings) should equal the cost of playing the game:
(1/12) × x = 5
Step 5: Solve the equation for x.
To solve for x, multiply both sides of the equation by 12:
x = 5 × 12
x = 60
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
sketch the region bounded by the curves 2x2 y=202x2 y=20 and x4−y=4x4−y=4, then find the area of the region.
Answers
The area of the region bounded by the curves is approximately 72.75 square units.
What is parabola?A parabola is the portion of a right circular cone cut by a plane perpendicular to the cone's generator. It is a locus of a point that moves such that the separation between it and a fixed point (focus) or fixed line (directrix) is the same.
To sketch the region bounded by the curves 2x² - y = 20 and x⁴ - y = 4, we can begin by graphing each equation separately.
First, the equation 2x² - y = 20 can be rearranged to solve for y:
y = 2x² - 20
This is a downward-facing parabola that opens towards the vertex at (0, -20).
Next, the equation x⁴ - y = 4 can be rearranged to solve for y:
y = x⁴ - 4
This is an upward-facing parabola that opens towards the vertex at (0, -4).
To find the intersection points of the two curves, we can set the right-hand sides of the equations equal to each other:
2x² - y = 20
x⁴ - y = 4
Substituting y from the second equation into the first equation, we get:
2x² - (x⁴ - 4) = 20
Simplifying and rearranging, we get:
x⁴ - 2x² - 24 = 0
Factoring, we get:
(x² - 4)(x² + 6) = 0
This gives us four solutions:
x = ±2 and x = ±√6
Substituting these values of x into either of the original equations, we can find the corresponding y-values:
When x = 2, y = 4
When x = -2, y = 36
When x = √6, y = 2(6)² - 20 = 32
When x = -√6, y = 2(6)² - 20 = 32
So the intersection points are (2, 4), (-2, 36), (√6, 32), and (-√6, 32).
To sketch the region bounded by the curves, we can plot the two curves and shade the area between them:
The area of this region can be found by integrating the difference between the two curves with respect to x:
A = ∫[√6, 2] [(x⁴ - 4) - (2x² - 20)] dx
Simplifying, we get:
A = ∫[√6, 2] (x⁴ - 2x² + 16) dx
Integrating term by term, we get:
A = [x⁵/5 - 2x³/3 + 16x]√6 to 2
Evaluating this expression, we get:
A ≈ 72.75
So, the area of the region bounded by the curves is approximately 72.75 square units.
Learn more about parabola on:
https://brainly.com/question/9201543
#SPJ4
Two magnets will attract one another if
Answers
Answer:
the rule to remember is that opposites attract. every magnet has both a north and a South pole. when you place the North Pole of one magnet near the South Pole of another magnet, they are attracted to one another.
Step-by-step explanation:
Hope this helped Mark BRAINLIEST!!
Answer:
The magnets have different poles facing each other ( N/S > < S/N )
the blenders produced by a company have a normally distributed life span with a mean of 8.2 years and a standard deviation of 0.8 years. the company is willing to have a warranty that replaces at most 6% of their blenders sold. what is the longest a blender can last and still be in the lowest 6% of life spans?
Answers
The longest a blender can last and still be in the lowest 6% of life spans is 7.96 years.
The longest a blender can last and still be in the lowest 6% of life spans is calculated by using the inverse normal distribution formula. This formula is P(X ≤ x) = 1 - P(X > x). The X is the longest a blender can last and P(X ≤ x) is 6%. First, we need to calculate the z-score for 6%. This can be done by P(X ≤ x) = 0.06 and using the z-score formula z = (x - μ) / σ , where μ is the mean and σ is the standard deviation. Substituting the values into the equation, we get z = 0.06 = (x - 8.2) / 0.8. Solving for x gives us x = 7.96. Therefore, the longest a blender can last and still be in the lowest 6% of life spans is 7.96 years.
Learn more about normal distribution here:
https://brainly.com/question/29509087
#SPJ4
Find the average value fave of the function f on the given interval. f(x) = x2 (x3 + 30) [-3, 3] = fave Find the average value have of the function h on the given interval. In(u) h(u) = [1, 5] u = h ave Find all numbers b such that the average value of f(x) = 6 + 10x - 9x2 on the interval [0, b] is equal to 7. (Enter your answers as a comma-separated list.) b = Suppose the world population in the second half of the 20th century can be modeled by the equation P(t) = 2,560e0.017185t. Use this equation to estimate the average world population to the nearest million during the time period of 1950 to 1980. million people
Answers
Answer:
Step-by-step explanation:
To find the average value of the function f(x) = x^2(x^3 + 30) on the interval [-3, 3], we use the formula:
fave = (1/(b-a)) * ∫[a,b] f(x) dx
where a = -3 and b = 3.
So, we have:
fave = (1/(3-(-3))) * ∫[-3,3] x^2(x^3 + 30) dx
fave = (1/6) * [∫[-3,3] x^5 dx + 30∫[-3,3] x^2 dx]
fave = (1/6) * [0 + 30(2*3^3)]
fave = 2430
Therefore, the average value of the function f on the given interval is 2430.
To find the average value of the function h(u) = In(u) on the interval [1, 5], we use the formula:
have = (1/(b-a)) * ∫[a,b] h(u) du
where a = 1 and b = 5.
So, we have:
have = (1/(5-1)) * ∫[1,5] ln(u) du
have = (1/4) * [u ln(u) - u] from 1 to 5
have = (1/4) * [(5 ln(5) - 5) - (ln(1) - 1)]
have = (1/4) * (5 ln(5) - 4)
have = 0.962
Therefore, the average value of the function h on the given interval is approximately 0.962.
To find all numbers b such that the average value of f(x) = 6 + 10x - 9x^2 on the interval [0, b] is equal to 7, we use the formula:
fave = (1/(b-a)) * ∫[a,b] f(x) dx
where a = 0 and b = b.
So, we have:
7 = (1/b) * ∫[0,b] (6 + 10x - 9x^2) dx
7b = [6x + 5x^2 - 3x^3/3] from 0 to b
7b = 2b^2 - 3b^3/3 + 6
21b = 6b^2 - b^3 + 18
b^3 - 6b^2 + 21b - 18 = 0
Using synthetic division, we find that b = 2 is a root of this polynomial equation. Dividing by (b-2), we get:
(b-2)(b^2 - 4b + 9) = 0
The quadratic factor has no real roots, so the only solution is b = 2.
Therefore, the only number b such that the average value of f(x) on the interval [0, b] is equal to 7 is 2.
To estimate the average world population to the nearest million during the time period of 1950 to 1980, we need to find:
ave = (1/(1980-1950)) * ∫[1950,1980] P(t) dt
ave = (1/30) * ∫[1950,1980] 2560e^(0.017185t) dt
Using the formula for integrating exponential functions, we get:
ave = (1/30) * [2560
I need this one quick it depends on my first grade for this quarter, What is the equation of the line that passes through the points (4, 15) and (0, 3)?
A.
B.
C.
D.
Answers
Answer:
y=3x+3
Step-by-step explanation:
Explain why the gradient of BC is the same as the gradient of AD.
Answers
The gradient of BC is the same as the gradient of AD because the lines are parallel lines
How to explain why the gradients are equalGiven that
Lines BC and AD
For the gradients to be equal, then the lines are parallel lines
The gradients of parallel lines are equal because parallel lines have the same slope.
Since parallel lines have the same orientation and do not intersect, they have the same change in y-coordinates and change in x-coordinates.
Therefore, the ratio of the change in y-coordinates to the change in x-coordinates, which is the slope, is the same for both parallel lines.
Read more about slope and gradients at
https://brainly.com/question/29135291
#SPJ1
Find the slope of the line that passes through (9,4) and (4,11)
Answers
hope this helps
The value of a movie poster is increasing at a rate of 3.5% per
year. In 1990, the poster was worth $20.25. Find the value of the
poster in 2013.
Answers
Answer:
44.55
Step-by-step explanation:
I actually didn't get the right answer and I just edited it right now I'm sorry I dont have an explanation!
find the least positive integer $n$ such that no matter how $10^n$ is expressed as the product of two positive integers, at least one of these two integers contains the digit 0.
Answers
The least positive integer $n$ such that no matter how $10^n$ is expressed as the product of two positive integers, at least one of these two integers contains the digit 0, is 7.
Latex formula for equation.
f(x) = x^2 + 2x + 1
Let's consider the factorization of $10^n$ for increasing values of $n$.
For $n = 1$, $10^1 = 10$ which contains the digit 0.
For $n = 2$, $10^2 = 100$ which contains the digit 0.
For $n = 3$, $10^3 = 1000$ which contains the digit 0.
For $n = 4$, $10^4 = 10,000$ which contains the digit 0.
For $n = 5$, $10^5 = 100,000$ which contains the digit 0.
For $n = 6$, $10^6 = 1,000,000$ which contains the digit 0.
For $n = 7$, $10^7 = 10,000,000$ which contains no digit 0.
Therefore, the least positive integer $n$ is 7.
To learn more about least positive integer please click on below link.
https://brainly.com/question/28393783
#SPJ4
Three times the square of a non-zero
number is equal to twelve times the
number.
Answers
3x^2-12x=0
3x(x-4)=0
x=0, 4
the answer is 4
What is 0.44% of 625?
Answers
Answer:
2.75 i believe
Answer:
2.75
Step-by-step explanation:
\(625*\frac{0.44}{100} =2.75\)
how many numbers do you need to win the ohio classic lotto
Answers
To win the Ohio Classic Lotto, you need to match all six numbers drawn. In this lottery game, players choose six numbers from a set range, typically from 1 to 49.
The winning combination is determined by a random drawing of six numbers, usually conducted by a lottery machine or ball-drawing mechanism.
For a chance to win the jackpot prize, you must have all six numbers on your ticket match the six numbers drawn in the official drawing. This means that every number on your ticket must exactly correspond to the numbers selected in the drawing, and in the same order.
Matching fewer than all six numbers does not result in winning the jackpot prize. However, depending on the specific rules of the Ohio Classic Lotto, there may be secondary prizes for matching a subset of the drawn numbers, such as matching five, four, or three numbers correctly. These secondary prizes are typically of smaller value than the jackpot prize.
In summary, to win the Ohio Classic Lotto, you need to match all six numbers in the drawing.
Learn more about numbers here:
https://brainly.com/question/3589540
#SPJ11
Find the missing side of a right triangle if side a=7 and side b=11.
Answers
Step-by-step explanation:
c² = a² + b²
c² = 7² + 11²
c² = 49 + 121
c² = 170
now u have to square root it
c² = 170
c = 13
A poll agency reports that 27 % of teenagers aged 12-17 own smartphones. A random sample of 85 teenagers is drawn. Round your answers to at least four decimal places as needed.
Answers
Answer:
Mean = цр = 0.27
Step-by-step explanation:
Note: The full question is attached as picture below
Given that, p = 27 = 0.27 and n = 85
цр = P
Mean = цр = 0.27

A tv show had 3.6 x 104 viewers in the first week and 4.1 x 104 viewers in the second week. determine the average number of viewers over the two weeks and write the final answer in scientific notation. 3.85 x 104 7.7 x 104 3.85 x 108 7.7 x 108
Answers
The average number of viewers over the two weeks written in scientific notation is 3.85 × 10^8. option C
Scientific notationFirst week = 3.6 x 10⁴Second week = 4.1 x 10⁴Average number of viewers over the two weeks = (First week + Second week) / 2
= {(3.6 x 10⁴) + (4.1 x 10⁴)} / 2
= {3.6 + 4.1 × 10^(4×4) } / 2
= (7.7 × 10^16) / 2
= 3.85 × 10^8
Therefore, the average number of viewers over the two weeks written in scientific notation is 3.85 × 10^8.
Learn more about scientific notation:
https://brainly.com/question/27862246
#SPJ4
a painter leans a 10 foot ladder against a house. the base of the ladder is 6 feet from the house. how high on the house does the ladder reach?
Answers
Answer:
7Ft
Step-by-step explanation:
(7ft) Because of Pythagorean Thm. Since the ladder is leaning against a building it makes 10ft the hypotenuse,
Simplify (6x^2 − 8x) ÷ (2x) step by step
a. 2x − 3
b. 2x + 3
c. 3x − 4
d. 3x − 8
Answers
Answer:
3x - 4
Step-by-step explanation:
(6x^2 − 8x) ÷ (2x) =
(6x^2)/2x - 8x/2x =
3x - 4
Answer:
(C). 3x - 4
Step-by-step explanation:
It will be easily to break this down so,
6/2=3
x^2/x=x
therefore, 6x^2/2x = 3x
Minus stay minus
8/2 = 4
x/x=1
therefore, 8x/2x=4
If we put it all together,
3x - 4
if this helps you, please give brainliest!
solve the linear equation 4x-(2x-1)=x+5+x-6
Answers
The linear equation doesn't have a solution.
How to compute the value?The linear equation given is illustrated as: 4x-(2x-1) = x+5+x-6
This will be solved thus:
4x - 2x + 1 = x+5+x-6
4x - 2x + 1 = 2x - 1.
2x + 1 = 2x - 1
Collect like terms
2x - 2x = -1 - 1
0 = -2
This illustrates that the equation doesn't have a solution.
Learn more about equations on:
brainly.com/question/28280501
#SPJ1
The system defined by the input-output relation y(u) -x() cos(2T fo), where fo is a constant, is called a modulator. Is this system linear? Is it time invariant?
Answers
The system with an input-output relation y(u) -x() cos(2T fo), where fo is a constant, is linear but not time-invariant.
To determine whether the system defined by the input-output relation y(u) = x(t) cos(2πf0 t) is linear or time-invariant, we need to apply the superposition principle and the time-invariance test.
Linearity:
A system is linear if it satisfies the superposition principle, which states that the response to a sum of inputs is equal to the sum of the individual responses to each input. Mathematically, this can be expressed as:
y(u) = a1x1(u) + a2x2(u)
where a1 and a2 are constants, x1(u) and x2(u) are two arbitrary input signals, and y(u) is the corresponding output.
Let's apply this principle to the given system:
y1(u) = x1(t) cos(2πf0 t)
y2(u) = x2(t) cos(2πf0 t)
y(u) = y1(u) + y2(u) = x1(t) cos(2πf0 t) + x2(t) cos(2πf0 t)
This is a sum of two inputs, and the output is the sum of the individual responses to each input. Therefore, the system is linear.
Time-Invariance:
A system is time-invariant if its behavior does not change over time. In other words, if the input signal is shifted in time, the output signal is also shifted by the same amount of time.
Let's test the time-invariance of the given system:
Assume the input signal is x1(t), and the corresponding output is y1(t) = x1(t) cos(2πf0 t).
Now, let's shift the input signal by a time τ to get a new input signal x2(t) = x1(t-τ). The corresponding output is y2(t) = x2(t) cos(2πf0 t) = x1(t-τ) cos(2πf0 t).
Let's compare the two outputs:
y2(t) = x1(t-τ) cos(2πf0 t)
y1(t-τ) = x1(t-τ) cos(2πf0 (t-τ))
We can see that y2(t) and y1(t-τ) are not equal, which means the system is not time-invariant.
Know more about time-invariant here:
https://brainly.com/question/31041284
#SPJ11
in multiplying two positive integers a and b, ron reversed the digits of the two-digit number a. his erroneous product was 161. what is the correct value of the product of a and b?
Answers
The correct value of the product of a and b is 224
Taking the prime factorization of 161 reveals that it is equal to 23*7. Therefore, the only ways to represent 161 as a product of two positive integers are 161*1 and 23*7. Because neither 161 nor 1 is a two-digit number, the only two-digit factor of 161 is 23, we know that a and b are 23 and 7. Because 23 is a two-digit number, we know that a, with its two digits reversed, gives 23.
Therefore, a = 32 and b = 7. Multiplying our two correct values of a and b yields.
The correct product must have been
a*b =32*7
=224
Learn more about multiplying positive integers here: https://brainly.com/question/11453536
#SPJ4
Guys plz help me solve this question I’ve been trying for the past 40 minutes.

Answers
Answer:
x= -1.8
Step-by-step explanation:
4x-22=9x+2(1-4x)
2(1 - 4x)
so you have to distribute
new equation
4x-22=9x+2-8x
you combine like terms on the right
9x + 2 -8
+8. +8
17x+2
new equation
4x-22=17x+2
-4x. -4x
-22=13x + 2
-2. -2
-24=13x
-24÷13= - 1.8
X= -1.8
Answer:
\(4x - 22 = 9x + 2 - 4x \\ - x = 24 \\ x = - 24\)