Mr Bagley has a dog that can run 37.35 miles per hour. He also has a horse that can run 47.5 miles per hour. How much faster can the horse run than the dog
Answers
Answer:
10.15
Step-by-step explanation:
47.5-37.35=10.15
Related Questions
What is the product of 2 over 3y and y?
12 over 3y
2 over 3
2 over 3y
22 over 3y
Answers
The product of 2/3y and y is \(2/3y^2.\)
The product of 2/3y and y can be found by multiplying the numerators and denominators separately.
To multiply the numerators, we multiply 2 and 1 (since y can be written as y/1).
This gives us 2.
To multiply the denominators, we multiply 3y and 1.
This gives us 3y.
Therefore, the product of 2/3y and y is \(2/3y * y =\) \(2/3y^2.\)
In general, when multiplying fractions, we multiply the numerators and the denominators separately.
So, if we have a fraction a/b and another fraction c/d, their product would be ac/bd.
However, in this specific case, the expression can be simplified further.
Since we have y in both the numerator and denominator, they cancel out, leaving us with \(2/3y^2.\)
To summarize, the product of 2/3y and y is \(2/3y^2.\)
For more questions on product
https://brainly.com/question/28782029
#SPJ8
Part A: A statement about rational numbers is shown.
The product of two negative rational numbers is greater than either factor. Is the statement always true, sometimes true, or never true? Explain your answer. Provide at least two examples to support your answer.
Part B: A different statement about rational numbers is shown.
The product of two positive rational numbers is greater than either factor. Provide at least two examples to show that this statement is only sometimes true.
Answers
i didn’t realize u were chill like that
Usain Bolt ran miles in of an hour. A domestic cat runs miles in 9 4 153 1 3 4 3 8 1 of an hour. Would Usain Bolt or a domestic cat win a race?
Answers
Answer:
The Usain Bolt it ran more miles in a shorter amount of time
Step-by-step explanation:
The Usain Bolt ran over 9 miles in only 1/3 of an hour while the cat ran 3 miles in 1/8 of an hour
Solve the equation for x, and enter your answer below.
10x - 15x + 5= -45 + 40
Answers
Answer: x = 2
Step-by-step explanation:
\(10x - 15x + 5= -45 + 40\)
subtract 5
\(10x - 15x= -45 + 40-5\)
Combine like terms;
\(-5x=-10\)
Divide by -5
\(x=\frac{-10}{-5}\\ x=2\)
Answer:
\(x = 2\)
Step-by-step explanation:
\(10x - 15x + 5 = - 45 + 40 \\ 10x - 15x = - 5 - 45 + 40 \\ - 5x = - 10 \\ \frac{ - 5x}{ - 5} = \frac{ - 10}{ - 5} \\ x = 2\)
Linear Programming - A student has 30 minutes to complete an exam. There are 9 multiple
choice questions worth 3 points each. There are also 3 short answer questions worth 5 points each
It takes about 2 minutes to answer a multiple choice question and about 6 minutes to complete a
short answer question. How many multiple choice questions and short answer questions should the
student answer to maximize his score in the time remaining (Use x = multiple choice y = short
answer.)
3.). State the Objective Function (S for score) in the linear programming problem given
Answers
In this linear programming problem, the objective function (S) would be to maximize the student's score within the 30-minute time limit, given by:S = 3x + 5y.Where x represents the number of multiple choice questions answered and y represents the number of short answer questions answered. The objective is to maximize the total score, which is the sum of the scores for each type of question.
To maximize the student's score within the given time constraint, we can use linear programming. Let's define the variables:
x = number of multiple choice questions answered
y = number of short answer questions answered
The Objective Function (S for score) represents the total points the student can get, which can be calculated as:
S = 3x + 5y
Now, we need to consider the constraints:
1. Time constraint: 2x + 6y ≤ 30 (it takes 2 minutes for a multiple choice question and 6 minutes for a short answer question)
2. Number of questions constraint: x ≤ 9 (there are only 9 multiple choice questions available)
3. Number of questions constraint: y ≤ 3 (there are only 3 short answer questions available)
4. Non-negative constraint: x, y ≥ 0 (a student can't answer a negative number of questions)
By solving this linear programming problem, the student can find the optimal number of multiple choice and short answer questions to answer in order to maximize their score within the given time frame.
To learn more about limit : brainly.com/question/8533149
#SPJ11
What is the area of this polygon

Answers
Answer:
51
Step-by-step explanation:
1. Approach
One is given the polygon, (ABCDE); the problem asks one to find the area of this polygon. The most logical step to take is to divide this polygon into easier parts, find the area of each part, and then add up the area to find the total area of the figure.
One way to divide this figure up is to draw the line (AC). This will create the triangle (ABC) and rectangle (ACDE).
2. Find the area of (ABC)
The formula to find the area of a triangle is the following:
\(A=\frac{b*h}{2}\)
Where (b) is the base of the triangle, and (h) is the height. The base of the triangle (ABC) is (AC), which has a measure of (6) units. The height of the triangle is the distance from the base of the triangle to the vertex opposite the base. This measurement is (3) units. Substitute these values into the formula and solve for the area:
\(A=\frac{b*h}{2}\)
Substitute,
\(A=\frac{6*3}{2}\\\\A=\frac{18}{2}\\\\A=9\)
3. Find the area of (ACDE)
The formula to find the area of a rectangle is as follows:
\(A=b*h\)
The base of the rectangle is the segment (AE), with a measure of (7) units. The height of the rectangle is the segment (AC) with a measurement of (6) units. Substitute these values into the formula and solve for the area:
\(A=7*6\\\\A=42\)
4. Find the area of the total figure
To find the area of the total figure, add up the area of the triangle, and the area of the rectangle:
\(9+42= 51\)
what is the value of z?
420
60
440
240

Answers
question 5 a data analyst is collecting a sample for their research. unfortunately, they have a small sample size and no time to collect more data. what challenge might this present?
Answers
Answer: A small sample size hampers statistical power, generalizability, precision, and the ability to conduct robust analyses, ultimately impacting the reliability and validity of the research findings
Step-by-step explanation:
Having a small sample size can present several challenges for a data analyst conducting research. One primary challenge is the issue of statistical power. With a small sample size, the analyst may not have enough data points to detect meaningful or significant effects or relationships accurately. This can lead to limited generalizability of the findings to the broader population or limited ability to draw valid conclusions.
Additionally, a small sample size can result in increased sampling error and variability. The findings may be more susceptible to random fluctuations, making it difficult to establish reliable patterns or trends.
Furthermore, a small sample size may limit the analyst's ability to conduct in-depth subgroup analysis or explore complex interactions between variables. It may also limit the precision of estimates and confidence in the research outcomes.
In summary, a small sample size hampers statistical power, generalizability, precision, and the ability to conduct robust analyses, ultimately impacting the reliability and validity of the research findings.
For more questions on research findings
https://brainly.com/question/17137063
#SPJ11
A small sample size can present challenges for a data analyst in terms of reduced statistical power, reduced representativeness of the population, and increased sensitivity to outliers.
Explanation:A small sample size presents several challenges for a data analyst conducting research.
The main challenge is to do with statistical power, which is the probability that a statistical test will detect a significant difference when one actually exists. With a small sample size, the statistical power is reduced, meaning there's a higher chance you won't detect a significant effect even if it is present i.e you might make a Type II error.The second challenge revolves around the fact that smaller samples are less likely to be representative of the population. The representativeness of a sample affects the external validity of the results, meaning that it affects how well the findings can be generalized to the broader population. Lastly, outliers can have a larger impact in a small dataset, skewing the results and possibly leading to incorrect conclusions.Learn more about Challenges of small sample size here:https://brainly.com/question/34941067
#SPJ12
Ignore the chosen answer mark thing I clicked on it by accident

Answers
Answer:
It's the one you clicked!
Step-by-step explanation:
It is 22.5 or 22 \(\frac{1}{2}\)
because
5/2 simplified is 2.5
2.5 x 9 = 22.5
hope this helps :)
When p(x) = 9x4- 45x3 + 37x2 + x +2 is divided by x - 2, a student can determine the
remainder by evaluating p(2). What is the value of p(2)?
1
2
P(2) = 652
P(2) = 656
P(2) = -368
P(2) = -64
Answers
Answer:
-64
Step-by-step explanation:
The option that gives the correct answer when we evaluate p(2) of the given polynomial is; Option D; P(2) = -64
We are given the polynomial;
p(x) = 9x⁴ - 45x³ + 37x² + x + 2
We are told he wants to determine the remainder by evaluating p(2). This means we will plug in 2 for x in the polynomial to get the remainder.
Thus;
p(2) = 9(2)⁴ - 45(2)³ + 37(2)² + 2 + 2
p(2) = 9(16) - 45(8) + 37(4) + 4
p(2) = 144 - 360 + 148 + 4
p(2) = -64
In conclusion, p(2) = -64 and Option D is the correct option.
Read more at; https://brainly.com/question/18387716
14b + 6 = 6 14b = Subtract 6 from both sides b = Divide both sides by 14
Answers
Answer:
Step-by-step explanation:
((b+2)(b+12)/(b+2)(b+3))*(b+3)
= (b+12)
Which row in the table is closest to the actual solution?
Var +3
+2
0
2
2.7321
L79
0.1
20196
02
2.8139
2.0385
03
1.897
20566
0
1.9494
2011
05
2
2.0909
0.6
20194
21071
0.7
2.0976
21208
21379
0.8
21418
21909
21595
1.0
2.2361
2.1667
Answers
Answer:
0.8= 2.1448=2.1379
Step-by-step explanation:
Answer:
0.8/2.1448/2.1379
Step-by-step explanation:
I got right(Plato/Edmentum
Scarlett made seven dozen sugar cookies. She needs 138 cookies for the cookie exchange. How many more cookies does she still need to make?
I suck at math :/ but like my math teacher never did teach us
Answers
Answer:
54 cookies
Step-by-step explanation:
seven dozen means 7 * 12 cookies
because one dozen = 12 cookies, so having seven dozen means have seven, one dozen batches
seven dozen = 7*12 = 84 cookies
she already made 138
138 - 84 cookies = 54 cookies left to go
54 cookies
about ____ of the possible outcomes occur within one standard deviation of the mean\
Answers
Answer:
68%
Step-by-step explanation:
In normal distribution, the empirical rule (aka 68-95-99.7 rule) describes the approximate proportion of data that falls within certain distances from the mean of a normal distribution. Specifically, the rule states that:
About 68% of the data falls within one standard deviation of the mean.About 95% of the data falls within two standard deviations of the mean.About 99.7% of the data falls within three standard deviations of the mean.What is the justification for step 1 in the solution process? 15x − 8 = 14x + 13 Step 1: 15x = 14x + 21
Answers
Answer:
Step-by-step explanation:
b
The justification for Step 1 is the subtraction property of equality. Option B
What is the justification for step 1 in the solution process?The justification for Step 1 within the arrangement prepare, which changes the condition 15x − 8 = 14x + 13 into 15x = 14x + 21, is the subtraction property of uniformity.
The subtraction property of equality states that in the event that we subtract the same amount from both sides of an condition, the condition remains genuine. In this case, we are subtracting 14x from both sides of the condition to confine the term with x.
To clarify Step 1 utilizing the subtraction property of correspondence:
The condition 15x − 8 = 14x + 13 is given.
We need to disconnect the x term on one side of the condition. To do this, we got to dispose of the 8 on the cleared out side.
By subtracting 14x from both sides of the condition, we evacuate the 14x term from the correct side:
15x − 14x − 8 = 14x − 14x + 13
Simplifying:
x − 8 = 13
Now, the 14x term is dispensed with from the proper side of the condition.
To advance streamline the condition, we are able include 8 to both sides to dispose of the -8 term on the cleared out side:
x − 8 + 8 = 13 + 8
Simplifying:
x = 21
Now, we have effectively isolated the x term on one side of the condition.
Therefore, the justification for Step 1 is the subtraction property of equality (B).
Learn more about subtraction property of equality
https://brainly.com/question/1005442
#SPJ2
Complete question
What is the justification for step 1 in the solution process?
15x − 8 = 14x + 13
Step 1: 15x = 14x + 21
A.
the addition property of equality
B.
the subtraction property of equality
C.
the division property of equality
D.
the multiplication property of equality
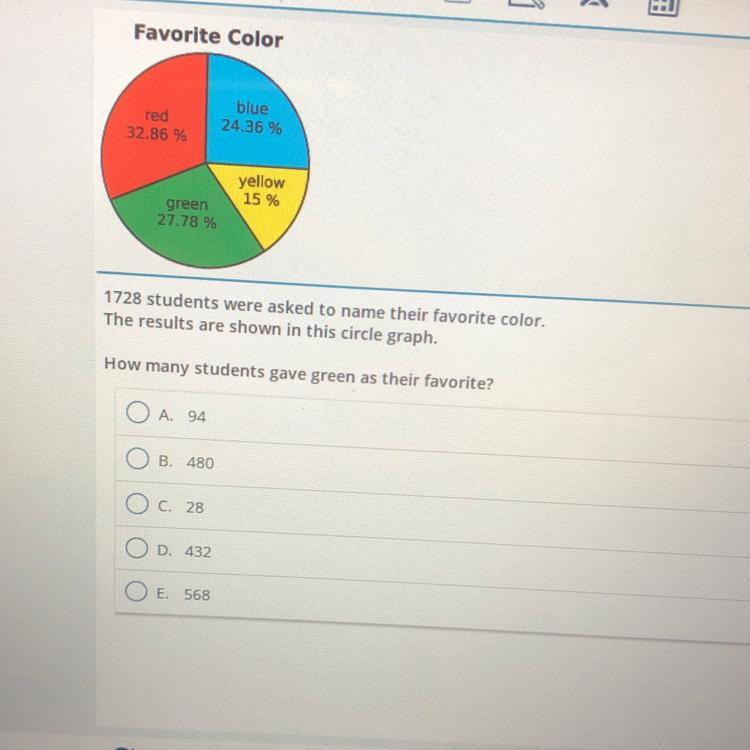
Favorite Color
red
32.86 %
blue
24.36 %
yellow
15 %
green
27.78 %
1728 students were asked to name their favorite color.
The results are shown in this circle graph.
How many students gave green as their favorite?
O A 94
OB. 480
O c. 28
D. 432
O E. 568
Answers
Answer:
I say 28
Step-by-step explanation:
because its 27 and it's almost to 28
Answer:
E. 568
Step-by-step explanation:
A certain television is advertised as a 95-inch tv (the diagonal length). if the width of the tv is 77 inches, how tall is the tv? round to the nearest tenth of an inch.
Answers
The height of the television given the length of its diagonal and its width is 55.6 inches
What the height of the tv?The height of the television can be determined using Pythagoras Theorem.
The Pythagoras theorem: a² + b² = c²
where a = length
b = base
c = hypotenuse
√95² - 77² = 55.6 inches
To learn more about Pythagoras theorem, please check: https://brainly.com/question/14580675
#SPJ1
Answer: 55.6
Step-by-step explanation: 55.6 that's what I put in and got it right
•Exercise #2. Suppose a market with two firms, 1 and 2, facing the inverse demand p()=10− p(Q)=10-Q where =1+2Q=q1+q2. The two firms incur a marginal cost of production c1=c2=2c1=c2=2, produce a homogeneous good, and are Cournot competitors.
•Q4) Draw the firms’ best-response functions with 1q1 on the vertical axis and 2q2 on the horizontal axis.
•Q5) Determine firm 2’s quantity at the Cournot equilibrium.
•Q6) Assume firm 1 adopts a raising rival’s cost strategy at the expense of firm 2. While firm 1’s marginal cost remains at c1=2c1=2, firm 2’s marginal cost increases to c2=4c2=4. On the same graph as the one used to answer Q4, show the effect of the raising rival’s cost strategy on the firms’ best-response functions.
•Q7) Determine firm 2’s quantity at the new Cournot equilibrium.
Q8) Determine the market price at the new Cournot equilibrium.
Answers
firm 2's quantity at the Cournot equilibrium is q2=5/3.the inverse demand function: p=10−Q=10−(q1+q2)=10−(11/5+4/5)=4. firm 2's quantity at the new Cournot equilibrium is q2=4/5.
The best response of firm 1 is given by 1q1=5−0.5q21+q2, and the best response of firm 2 is given by 2q2=5−0.5q12+q1. These best response functions are illustrated in the following diagram:
At the Cournot equilibrium, the two firms' quantities will be such that they are both choosing the best response to the other's quantity, which means that they will be producing where the two functions intersect.
Therefore, solving the two best response functions simultaneously for q1 and q2 gives:
q1=q2=5/3
Therefore, firm 2's quantity at the Cournot equilibrium is q2=5/3.
The new best response function for firm 2 is given by 2q2=5−q1+2q22. This is obtained by replacing c2=2 with c2=4 in firm 2's profit function. The new best response function is illustrated below:
At the new Cournot equilibrium, the two firms' quantities will be such that they are both choosing the best response to the other's quantity, which means that they will be producing where the two functions intersect. Therefore, solving the two best response functions simultaneously for q1 and q2 gives:
q1=11/5
q2=4/5
Therefore, firm 2's quantity at the new Cournot equilibrium is q2=4/5.
To determine the market price at the new Cournot equilibrium, we substitute the new equilibrium quantities into the inverse demand function:
p=10−Q=10−(q1+q2)=10−(11/5+4/5)=4
Therefore, the market price at the new Cournot equilibrium is p=4.
In this exercise, we consider a market with two firms, 1 and 2, facing the inverse demand p()=10− p(Q)=10-Q where =1+2Q=q1+q2.
The two firms incur a marginal cost of production c1=c2=2c1=c2=2, produce a homogeneous good, and are Cournot competitors. The best response of firm 1 is given by 1q1=5−0.5q21+q2, and the best response of firm 2 is given by 2q2=5−0.5q12+q1. These best response functions are illustrated in the diagram below:
At the Cournot equilibrium, the two firms' quantities will be such that they are both choosing the best response to the other's quantity, which means that they will be producing where the two functions intersect
. Therefore, solving the two best response functions simultaneously for q1 and q2 gives q1=q2=5/3. Therefore, firm 2's quantity at the Cournot equilibrium is q2=5/3.The new best response function for firm 2 is given by 2q2=5−q1+2q22. This is obtained by replacing c2=2 with c2=4 in firm 2's profit function.
The new best response function is illustrated in the following diagram:At the new Cournot equilibrium, the two firms' quantities will be such that they are both choosing the best response to the other's quantity, which means that they will be producing where the two functions intersect.
Therefore, solving the two best response functions simultaneously for q1 and q2 gives q1=11/5 and q2=4/5. Therefore, firm 2's quantity at the new Cournot equilibrium is q2=4/5
To determine the market price at the new Cournot equilibrium, we substitute the new equilibrium quantities into the inverse demand function: p=10−Q=10−(q1+q2)=10−(11/5+4/5)=4. Therefore, the market price at the new Cournot equilibrium is p=4.
In conclusion, we have analyzed the effect of a raising rival's cost strategy on a Cournot duopoly. We have shown that the strategy reduces firm 2's quantity and increases the market price, but does not affect firm 1's quantity.
To know more about demand visit:
brainly.com/question/30402955
#SPJ11
1. Robert and Casey added the following values shown below. Who solved
correctly?
ROBERT
CASEY
5 1/8+ 2 1/3 = 7 1/2
-4 1/2+ 6 3/4= 2 1/4
Answers
Answer:
Casey is correct.
Step-by-step explanation:
Robert's 5 1/8 + 2 1/3 = 7 1/2 is wrong because if 5+2 = 7, I would have to change the denominator of both fractions so they are both the same. The denominator would have to be 24. That would make the fractions 3/24 and 8/24. If you added them together, it would not be able to simplify to 1/2.
Casey's -4 1/2 + 6 3/4 = 2 1/4 is correct because —4 - 6 = 2. In order to make the fractions have the same denominator, you would have to multiply -1/2 by 2 on both numerator and denominator wich would equal -2/4. Now add -2/4 and 1/4 and you get 1/4. If my explaining is confusing, I'm sorry!☜(゚ヮ゚☜)
Casey is correct and he will get the correct solution.
We have given that,
ROBERT CASEY
5 1/8+ 2 1/3 = 7 1/2 -4 1/2+ 6 3/4= 2 1/4
Robert's 5 1/8 + 2 1/3 = 7 1/2 is wrong because if 5+2 = 7, I would have to change the denominator of both fractions so they are both the same.
What is the equation?A statement that the values of two mathematical expressions are equal.
The denominator would have to be 24.
That would make the fractions 3/24 and 8/24.
If you added them together, it would not be able to simplify to 1/2.
Casey is correct.
-4 1/2 + 6 3/4 = 2 1/4 is correct
because 4 - 6 = 2.
In order to make the fractions have the same denominator, you would have to multiply -1/2 by 2 on both numerator and denominator which would equal -2/4.
Now add -2/4 and 1/4 and you get 1/4.
To learn more about the equation visit:
#SPJ2
select wheather the equation have a solution or not square root x-1+4=0
Answers
The equation sqrt(x - 1) + 4 = 0 has a solution
How to check if the equation have a solutionThe equation sqrt(x-1) + 4 = 0 can be rewritten as:
√(x - 1) + 4 = 0
√(x - 1) = -4
Squaring both sides
(x - 1) = -4^2
(x - 1) = 16
solving for x
x = 16 + 1
x = 17
Learn more about solution of equations at:
https://brainly.com/question/13729904
#SPJ1
Please select the best answer from the choices provided.Simplify 2(csc^2theta - cot^2 theta) a. sin theta b. cos theta c. 2d. 1
Answers
Answer:
c
Step-by-step explanation:
using the identity
• 1 + cot²x = csc²x
given
2(csc²Θ - cot²Θ )
= 2(1 + cot²Θ - cot²Θ)
= 2(1)
= 2
What’s the answer bc I cannnot forgive this out rs

Answers
Answer:
x=0.41666666666666663,−0.916666666666666
Step-by-step explanation:
Its in the doc below


if 4b is equal to 3 what is b
Answers
Answer:
4b=3
b= 3/4
b=0.75
...........................
explanation:
4b=3
to get just the value of b, you need to divide by 4 on both sides as whatever happens to one side happens to the other
b=3/4
3/4 also equals 0.75
In the circle above, DE = 2, CE = 6, and BE = 3.
What is the measure of EA?
A) 2
B) 3
C) 6
D) 4

Answers
Answer: The correct option is (D) 4.
Step-by-step explanation:
According to the intersecting chords theorem, if two chords intersect in a circle then the products of the length of the chord segment are equal.
Given:
DE = 2
CE = 6
BE = 3
Now calculating the the value of EA.
As per theorem:
\(DE\times CE=BE\times EA\)
Now putting the all the given values in this expression, we get:
\(2\times 6=3\times EA\\\\EA=4\)
Therefore, the measure of EA is 4.
Jane has $d and wants to buy 3 beanie boos (in this problem they all cost the same. ) if she were to buy all three, she would spend all of her money. But she bought only one. How much money does jane have left?
Answers
Jane has (2/3)d dollars left after buying one beanie boo.
Let's call the cost of one beanie boo "x".
Then, if Jane wants to buy 3 beanie boos, she would spend 3x.
However, she only bought one beanie boo, so she spent x. We know that she spent all of her money, which is "d", so we can set up the equation:
3x = d (the cost of 3 beanie boos is equal to the amount of money Jane has)
To find out how much money Jane has left after buying one beanie boo, we need to subtract the cost of one beanie boo (x) from the total amount of money she has (d). We can solve for x by dividing both sides of the equation by 3:
3x/3 = d/3
x = d/3
Now we can substitute this value of x into our original equation:
3x = d
3(d/3) = d
d = d
So we can see that the amount of money Jane has is "d", and since she only spent "x" to buy one beanie boo, she has "d - x" left:
d - x = d - (d/3)
d - x = (2/3)d
Therefore, Jane has (2/3)d dollars left after buying one beanie boo.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ1
Subject to the conditions 0≤x≤10,0≤y≤5 the minimum value of the function 4x−5y+10 is (1) 10 (2) 0 (3) −25 (4) −15
Answers
The minimum value occurs when x = 10 and y = 0, resulting in a minimum value of 10.
To find the minimum value of the function 4x - 5y + 10 subject to the conditions inequality 0 ≤ x ≤ 10 and 0 ≤ y ≤ 5, we evaluate the function at the boundaries of the given conditions.
At the upper bound of x, when x = 10, the function becomes 4(10) - 5y + 10 = 40 - 5y + 10 = -5y + 50. Since y has a lower bound of 0, the minimum value of -5y + 50 occurs when y = 0, resulting in a value of 50.
At the lower bound of y, when y = 0, the function becomes 4x - 5(0) + 10 = 4x + 10. Similarly, since x has an upper bound of 10, the minimum value of 4x + 10 occurs when x = 10, resulting in a value of 50.
Comparing the values obtained at the boundaries, we find that the minimum value of the function 4x - 5y + 10 is 10.
Learn more about Inequality here
https://brainly.com/question/28823603
#SPJ11
prove that in a collection of 51 integers there is a subset of 11 where the difference of two of them is a multiple of 5
Answers
To prove that in a collection of 51 integers there is a subset of 11 where the difference of two of them is a multiple of 5, we can use the Pigeonhole Principle.
Consider the residues of the integers modulo 5, which can take values from 0 to 4. Let's assume that none of the 51 integers has a difference that is a multiple of 5. In other words, no pair of integers in the collection has a difference that leaves a residue of 0 when divided by 5.
Now, we can divide the 51 integers into five subsets based on their residues modulo 5. Each subset will contain the integers with the corresponding residues 0, 1, 2, 3, or 4.
Since we have 51 integers and only five possible residues, by the Pigeonhole Principle, at least one of the subsets must contain at least 51 / 5 = 10 + 1 = 11 integers. Let's assume, without loss of generality, that the subset with residue 0 contains 11 or more integers.
Within this subset, any pair of integers will have a difference that leaves a residue of 0 when divided by 5. Hence, we have found a subset of 11 integers where the difference of two of them is a multiple of 5.
Therefore, we have proved that in a collection of 51 integers, there is always a subset of 11 where the difference of two of them is a multiple of 5.
Learn more about subset here:
https://brainly.com/question/31739353
#SPJ11
What are all equivalent expressions to 4w+7w
Answers
Answer: 11w
Step-by-step explanation: you can add 4w and 7w since they both have the variable w.
Find the zeros and the vertical intercept of the function f(x) = -9x³+9x² - 2x. Give your answers as integers or reduced fractions. The zero(s) is/are ______
The horizontal intercept(s) is/are _____
Rhe vertical intercept is _____
Answers
The vertical intercept is (0, 0). Horizontal intercepts are the points where the graph of the function intersects the x-axis. At these points, the value of y is zero.
The function f(x) = -9x³+9x² - 2x can be factored as: -x(9x² - 9x + 2) .
The zeros can be obtained by setting the function equal to zero:-
x(9x² - 9x + 2) = 0
The zeros of the function are 0, 2/9, and 1.
To determine these solutions, we can use the Zero Product Property, which tells us that if the product of two factors is equal to zero, then at least one of the factors must be equal to zero. We can find the zeros of the function by setting each factor equal to zero and solving for x.
Thus, we have:Horizontal intercepts are the points where the graph of the function intersects the x-axis. At these points, the value of y is zero.
To find the horizontal intercepts, we set f(x) = 0 and solve for x.
Thus, we have:-9x³+9x² - 2x = 0x(-9x²+9x - 2) = 0
The horizontal intercepts of the function are -2/3, 0, and 2/3.
To determine these solutions, we can use the Zero Product Property, which tells us that if the product of two factors is equal to zero, then at least one of the factors must be equal to zero.
We can find the horizontal intercepts of the function by setting each factor equal to zero and solving for x.The vertical intercept is the point where the graph of the function intersects the y-axis.
At this point, the value of x is zero. To find the vertical intercept, we set x = 0 and evaluate the function. Thus, we have:
f(0) = 0 - 0 + 0 = 0.
Therefore, the vertical intercept is (0, 0).
To know more about vertical intercept visit :-
https://brainly.com/question/30820723
#SPJ11
.
Graph the point (9,0) on the coordinate plane.
Answers

Answer:
here mate.............
