Multiply. Write your answer as a fraction in simplest form.
5/6(−8/15)=
Answers
Answer:
-4/9
Step-by-step explanation:
I used a calculator.
5/6(−8/15) in simplest form is -4/9.
What is a fraction ?A fraction is written in the form of a numerator and a denominator.There are two types of fractions. One is proper fraction in which numerator is less than the denominator and another one is improper fraction in which denominator is less than the numerator.All fractions can be written in the form of p/q, where q ≠ 0 cause anything divided by 0 is undefined.
According to the given questions we have to multiply two fractions (5/6)(-8/15) which is
= -40/90.
= -4/9.
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ2
Related Questions
A weight attached to the end of a long spring is bouncing up and down. As it bounces, its distance from the floor varies sinusoidally with time. You start a stopwatch. When the stopwatch reads 1.7 seconds the spring is 58 cm above the floor and is on a downward path. It takes 4.4 seconds for the spring to bounce from a distance of 36 cm to 80 cm above the ground.
A. Write an equation expressing distance from the floor in terms of the number of seconds the stopwatch reads
B. Predict the distance from the floor when the stopwatch reads 6 seconds
C. What was the distance from the floor when you started the stopwatch?
Answers
The answers to all parts are shown below.
what is wave Equation?One of the most crucial equations in mechanics is the wave equation. It describes the movement of fluid surfaces, such as water waves, in addition to the movement of strings and wires.
Define constants:
t0 = 1.7seconds h0 = 58cm highest point
t1 = 4.4 seconds h1 = 44 cm lowest point
t2 = 6 seconds h2 = (h0 + h1)/2 = 51 cm center height
Half a cycle passes between t0 and t1, so the period T is
T = 2(t1 - t0) = 2(4.4-1.7) seconds = 5.4 seconds
The amplitude A is half the total height change between h0 and h1:
A = (h0 - h1)/2 = 7 cm
a) Equation of motion in terms of height H above the floor is
H(t) = h2 + A Co s[2π(t - t0)/T]
H(t) = 51 cm + (7cm) Cos[0.1775(t - 1.7second)/second]
b) Let t = 6 seconds in the equation:
H(t) = 51 cm + (7cm) Cos[0.1775(6 - 1.7second)/second]
= 51 + 7 x (-0.4008)
= 48.1944 cm
c) Let t = 0 seconds in the equation:
H(0 seconds) = 51 cm + (7cm) Cos[0.1775(0 - 1.7second)/second]
= (51+ 7[0.99999986]) cm
= 57.99cm
Learn more about Wave Equation here:
https://brainly.com/question/12931896
#SPJ1
If y varies directly with x and y=-16 when x=8, find y when x=2
Answers
Answer:
y=-4
Step-by-step explanation:
The answer is going to be -4 as when y=-16 x=8.
need help asap. low geometry grade

Answers
Answer:
x=9.3
Step-by-step explanation:
use SohCahToa
in this case u use cos
cos(41°)=7/x
x=7/cos(41)
x=9.275090953
x=9.3
I will give brainlyest

Answers
Answer:
\(\frac{10}{11}\)
Step-by-step explanation:
The formula for the trigonometric function sin is:
\(sin\)Ф\(=\frac{opposite}{hypotenuse}\)
The side opposite to the ∠g is x, which is equal to 10
\(opposite=x\) \(x=10\)
the hypotenuse of the triangle is z, which is equal to 11
\(hypotenuse=z\) \(z=11\)
so the ratio is:
\(\frac{10}{11}\)
plz mark me brainliest. :)
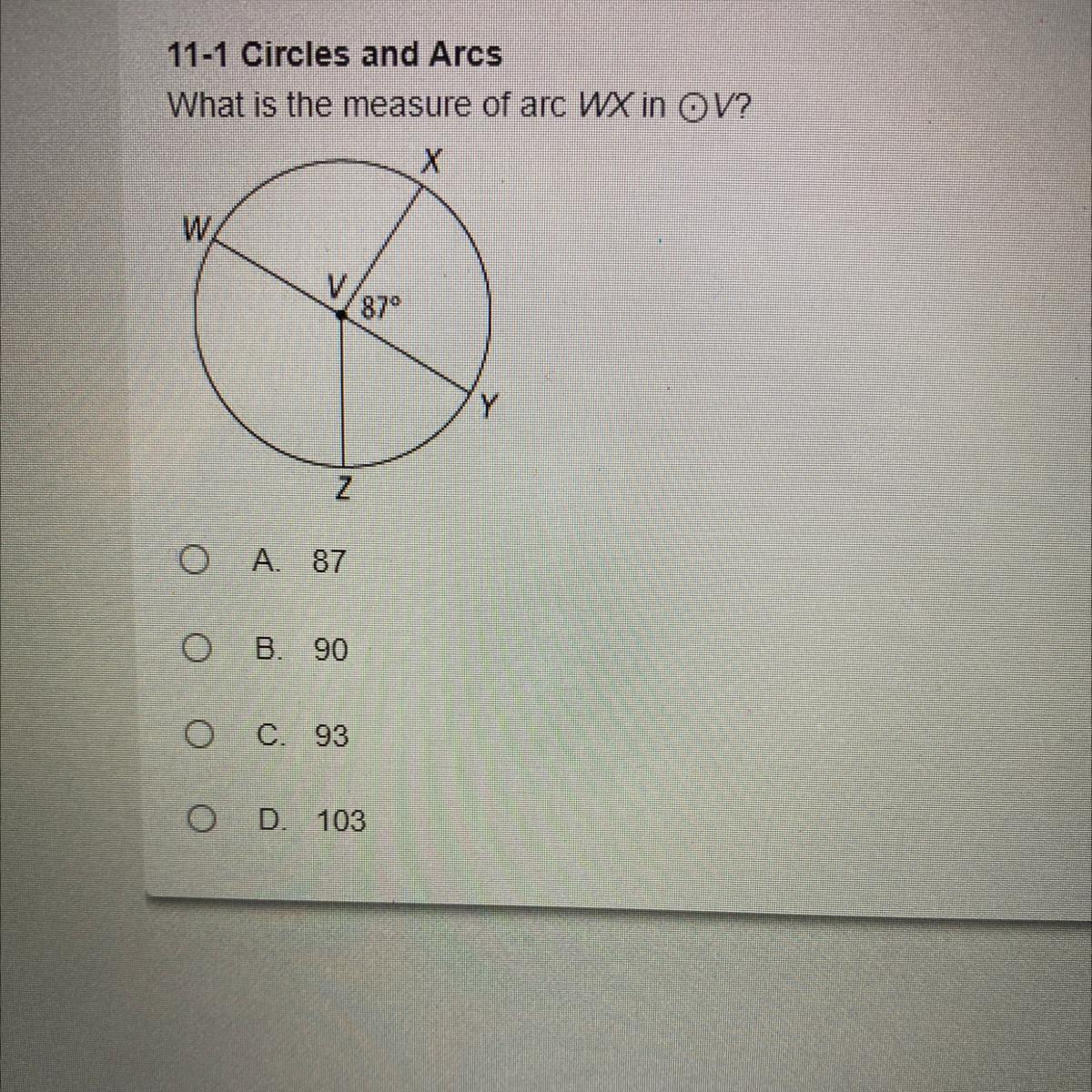
What is the measure of arc WX in V
A. 87
B. 90
C. 93
D. 103
(picture included) (please help, i need to pass this to pass the semester, will give brainliest answer)
Answers
Solve 35 < 7(2 - b) or 1/3 (15b – 12) greater or equal to 21.
Answers
Answer:
1) b = -3
2) b \(\geq\) 5
Step-by-step explanation:
35 < 7(2 - b)
5 = 2-b
3 = -b
b = -3
1/3 (15b – 12) \(\geq\) 21
15b – 12 \(\geq\) 63
15b \(\geq\) 75
b \(\geq\) 5
The solution of first inequality is b < -3
And, The solution of the second inequality is b ≥ 5.
Here,
The first inequality is;
35 < 7 (2 - b)
And, The second inequality is;
\(\frac{1}{3} (15b - 12) \geq 21\)
We have to solve the inequality.
What is Inequality?
A relation by which we can compare two or more mathematical expression is called an inequality.
Now,
Solve the first inequality as;
35 < 7 (2 - b)
Divide both side by 7,
5 < 2 - b
Add b both side,
5 + b < 2 - b + b
5 + b < 2
Subtract 5 both sides,
5 + b - 5 < 2 - 5
b < -3
And,
The second inequality is solved as;
\(\frac{1}{3} (15b - 12) \geq 21\)
Multiply 1/3 both side,
\(15b - 12\geq 63\)
Add 12 both side,
\(15b - 12 + 12 \geq 63 + 12\\\\15b \geq 75\)
Divide 15 both side,
\(b \geq 5\)
Therefore, The solution of first inequality is b < -3
And, The solution of the second inequality is b ≥ 5.
Learn more about the inequality visit:
https://brainly.com/question/25275758
#SPJ2
Shelly wants to join crossfit. The gym charges an initial membership fee of $60 and a monthly fee of $120. She has $900 to spend on a CrossFit memmbership. Write and solve an equation too find the number of months that Shelly can be a CrossFit memeber.
Answers
Answer:
Shelly can be a CrossFit member is 8 Months
($60-900) / $120 = Months
Step-by-step explanation:
Joining the gym costs 60$ so that would be your first month, it then costs $120 every month after. So we would start by subtracting $60 from the total $900
$60 - $900 = $840
Next you would divide your remaning money ($840) by the amount of money it cost per month ($120).
$840 / $120 = 7 Months
7 months plus the Enitial Month
The total number of months that Shelly can be a CrossFit member is 8 Months.
Investors buy a studio apartment for $150,000. Of this amount, they have a down payment of $37,500. Their down payment is what percent of the purchase price? What percent of the purchase price would a $67,500 down payment be?
Answers
Answer: To find the percentage of the down payment to the purchase price, just multiply the down payment by 100 and divide the result by the purchase
i.e 15,000 x 100/ 150,000= 10%
Also for the second part, multiply the down payment by 100 and divide by the purchase price
i.e 67,500 x 100 / 150,000= 45%
Step-by-step explanation:
calculate the taylor polynomials 2 and 3 centered at =0 for the function ()=16tan().
Answers
Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
To find the Taylor polynomials centered at x = 0 for the function f(x) = 16tan(x), we can use the Taylor series expansion for the tangent function and truncate it to the desired degree.
The Taylor series expansion for tangent function is:
tan(x) = x + (1/3)x^3 + (2/15)x^5 + (17/315)x^7 + ...
Using this expansion, we can find the Taylor polynomials of degree 2 and 3 centered at x = 0:
Degree 2 Taylor polynomial:
P2(x) = f(0) + f'(0)(x - 0) + (1/2!)f''(0)(x - 0)^2
= 16tan(0) + 16sec^2(0)(x - 0) + (1/2!)16sec^2(0)(x - 0)^2
= 0 + 16x + 8x^2
Degree 3 Taylor polynomial:
P3(x) = P2(x) + (1/3!)f'''(0)(x - 0)^3
= 0 + 16x + 8x^2 + (1/3!)(48sec^2(0)tan(0))(x - 0)^3
= 16x + 8x^2
Therefore, the Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
Learn more about taylor polynomials at https://brainly.com/question/31978863
#SPJ11
Please help I don't understand!

Answers
The statement <S and <H are equal in measure is False
How to determine the true statement?The similarity statement is given as:
ΔRST is similar to ΔHGF
This means that:
Angles R and H are congruentAngles S and G are congruentAngles T and F are congruentHence, the statement <S and <H are equal in measure is False
Because S equals G and R equals H
Read more about similar triangles at:
https://brainly.com/question/14285697
#SPJ1
fill in the blank to show an example of the symmetric property:
If JK = ST, then _ = __
Answers
Consider the data below: Month Demand Jan 141 Feb 276 Mar 216 Apr 156 May 261 Jun 141 Jul 246 Aug 246 Sep 216 Oct 156 Nov 216 Predict the demand for December using 4-period moving average. a. 208 O b. 196 O c. 211 O d. 197 O e. 278
Answers
The prediction of demand for December using the four-period moving average is 211.
This is option c.
To predict the demand for December using the 4-period moving average, the first step is to calculate the average of the demand in each four-month period. Here is how to calculate it:
Month Demand Average
Jan 141
Feb 276
Mar 216
Apr 156 179.75
May 261
June 141 186
Jul 246
Aug 246
Seperti 216 233.25
Oct 156
Nov 216 196.25
We then take the average of the last four months' average demands, which are the averages from September to November:
Average of the last four-month demand average = (233.25 + 196.25 + 216) / 3 = 215.5
Therefore, the prediction of demand for December using the four-period moving average is approximately 216. The answer is option (c) 211 (Approx)
Learn more about demand at
https://brainly.com/question/14689874
#SPJ11
Amanda is using wire to construct a triangle for an art project. She has 4 inches of blue eirr and 8 inches of green wire. Amanda is going to buy some purple wire for the third side of her triangle. She needs to buy enough wire to make a triangle, but does not want to have any wire let over. What is the least amount and the greatest amount of purple wire she could buy?
Amana could buy more than ___ inches but less than ___ inches of purple wire.
Answers
Amanda could buy more than 4 inches but less than 8 inches of purple wire to make triangle.
For Amanda to make a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Therefore, the minimum amount of purple wire she could buy would be the sum of the lengths of the blue and green wires (4 inches + 8 inches = 12 inches), minus the length of the longest side (which is 8 inches), so 12 inches - 8 inches = 4 inches.
The maximum amount of purple wire she could buy would be the sum of the lengths of the two shorter sides (4 inches + 4 inches = 8 inches).
Learn more about triangle here
https://brainly.com/question/29868619
#SPJ4
define the term of mathematics ?
Answers
Answer:
it is an abstract science of number, quantity and space, either as abstract concept
A student solved the equation below by graphing. log subscript 6 baseline (x minus 1) = log subscript 2 baseline (2 x 2)
Answers
Answer:
I think it's A ,Forgive me if its wrong its not a 100%.
Step-by-step explanation:
But if it is correct, im glad to be of service
Write the word sentence as an equation. Then solve.
The difference between a number pand 6 is -14
Equation
Solution p=
25
Answers
Answer:
p - 6 = -14
p = -8
Step-by-step explanation:
The difference between a number p and 6 is -14
Let the number = p;
Equation:
difference between the numbers:
p - 6
equality;
p - 6 = -14
Equation; p - 6 = -14
Solution:
p - 6 = -14
add (+6) to both sides of the expression;
p - 6 + (+6) = -14 +(+6)
p = -8
Given A(2,14), B(2,3), C(4,2), and D(14,2) what is the distance of CD?

Answers
Answer: CD = 10
Step-by-step explanation:
Subtract the smaller one from the larger one.
D(14, 2) - C(4, 2)
First, you subtract the x-values:
14 - 4 = 10
Then, you subtract your y-values:
2 - 2 = 0
Since the y-value is 0 (since it is a straight line), your distance of CD is 10.
Hope this helps!
Which statement is the correct interpretation of the inequality −4 > −5?
On a number line, −4 is located to the left of 0 and −5 is located to the right of 0.
On a number line, −4 is located to the right of 0 and −5 is located to the left of 0.
On a number line, −4 is located to the right of −5.
On a number line, −4 is located to the left of −5.
Answers
Answer:
On a number line, −4 is located to the right of −5Step-by-step explanation:
We know that numbers increase from left to right on the number line.
- 4 > - 5 means:
- 4 is greater than -5 and therefore is located to the right of -5Correct choice is:
On a number line, −4 is located to the right of −5Answer:
On a number line, -4 is located to the right of 5!
Step-by-step explanation:
It is closer to the 0 therefore it is greater than 5 if you want more information...
<><><><<><><><><><><><><><><><><><><><><>
if you were to right a number line leading up to -8 - -7 - -6 etc..
then you would see and understand the value better! :D
Have a great week every one!!! / ( ` o w `o ) \
May 23, 8:49:32 PM
Watch help video
In physics lab, Austin attaches a wireless sensor to one of the spokes of a bicycle
wheel spinning freely on its axle. The sensor's height above the ground, in
centimeters, is given by the function h(t) = 7.46 cos(2(t-0.25)) + 38.86,
where t is time measured in seconds.
What is the minimum and what does it represent in this
context?
Answers
The minimum is 29 cm and it represents the sensor's minimum height above the ground.
How to interpret the graph of a cosine function?In Mathematics and Geometry, the standard form of a cosine function can be represented or modeled by the following mathematical equation (formula):
y = Acos(Bx - C) + D
Where:
A represents the amplitude.B = 2π/P.P represents the period.C represents the phase shift.D represents the center line (midline).By critically observing the graph which models the sensor's height above the ground (in centimeters) shown in the image attached below, we can reasonably infer and logically deduce that it has a minimum height of 29 centimeters.
In conclusion, the sensor's minimum height above the ground cannot exceed 29 centimeters.
Read more on cosine function here: brainly.com/question/26993851
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Consider a regular hexagon centered at (3,4). Describe a rotation that
will map this regular hexagon onto itself.
Answers
Answer:
36- degree rotation m8
Step-by-step explanation:
mark me brainliest :)
This is with tangents I have already figured out one portion of the problem please help

Answers
Answer:
-5
Step-by-step explanation:
when x is squared it will always be positive so x can be negative or positive
Answer:
Step-by-step explanation:
Tangents drawn to the circumference of a circle are equal.
x^2 + 8 = 33 Subtract 8 from both sides
x^2+8-8 = 33 - 8 Combine
x^2 = 25 Take the square root of both sides.
√x^2 = √25
x = ± 5
So x = 5.
x can also be - 5. The minus goes away when you calculate x^2
because x is squared, you can get two answers, but be very careful when doing geometry questions that the minus number is used in such a way that only a positive value will be left.
root 225 rational or irrational? plzz help urgent.
Answers
(order doesn't matter)

Answers
Answer:
Because there are 4 ways to pick red then 4 (C)
Answer:
it looks like it would be C
Step-by-step explanation:
You take two random samples from two distinct populations and calculate the following statistics:
= 52.6, s1 = 3.2, n1 = 28
= 49.3, s2 = 2.9, n2 = 29
k = degrees of freedom = 27 t = 4.07 p 0.0002 State a conclusion, based on the P-value and = .05, for the hypothesis test H0: = , Ha: > .
A. There's a difference between the two population means.
B. We don't have enough evidence to reject the null hypothesis that there's no difference between the means of the two populations.
C. Reject the null hypothesis in favor of the alternative that there's a difference between the two population means.
D. Reject the null hypothesis in favor of the alternative, which states that the mean of population one is greater than the mean of population two.
E. On average, the difference between the two populations is 4.07.
Answers
The answer is (D) Reject the null hypothesis in favor of the alternative, which states that the mean of population one is greater than the mean of population two.
What is Null hypothesis mean ?The null hypothesis assumes that any kind of difference between the chosen characteristics that you see in a set of data is due to chance.
The given information corresponds to a two-sample t-test, where we are testing the null hypothesis H0: μ1 = μ2 (there is no difference between the means of the two populations) against the alternative hypothesis Ha: μ1 > μ2 (the mean of population one is greater than the mean of population two).
The calculated t-value is 4.07, and the degrees of freedom are k = 27. The corresponding p-value is 0.0002.
Since the p-value is less than the significance level α = 0.05, we can reject the null hypothesis in favor of the alternative hypothesis. This means that we have enough evidence to conclude that there is a difference between the means of the two populations, and that the mean of population one is greater than the mean of population two.
So,the correct answer is (D) Reject the null hypothesis in favor of the alternative, which states that the mean of population one is greater than the mean of population two.
Learn more about Null hypothesis here
https://brainly.com/question/28920252
#SPJ1
a football stadium has 100,000 seats. in a game with full capacity people with the following ticket and associated cost attended the game: determine the number of people that attended the game in each cost cate- gory if the total revenue was $4,897,000, there were 11,000 more alumni than faculty, the number of public plus alumni together was 10 times the number of veterans, the number of faculty plus alumni together was the
Answers
The number of people that attended the game in each cost category is Faculty: 7,000,Alumni: 18,000,Public: 18,000,Veterans: 4,000
To determine the number of people that attended the game in each cost category, to consider the given information and set up a system of equations to solve for the unknowns. Let's break down the problem step by step.
Let's denote the number of people in each cost category as follows:
Faculty: F
Alumni: A
Public: P
Veterans: V
The number of alumni is 11,000 more than the faculty, so we have the equation:
A = F + 11,000
The number of public plus alumni together was 10 times the number of veterans, so the equation:
P + A = 10V
The number of faculty plus alumni together was the same as the number of veterans, so we have the equation:
F + A = V
The total number of people attending the game is the sum of the people in each category, so the equation:
F + A + P + V = 100,000
Now, use these equations to solve for the unknowns.
First, substitute equation 1 into equations 2 and 3:
P + (F + 11,000) = 10V
F + (F + 11,000) = V
Simplify these equations:
P + F + 11,000 = 10V
2F + 11,000 = V
Next, substitute these equations into equation 4:
F + (F + 11,000) + P + (2F + 11,000) = 100,000
Simplify and combine like terms:
4F + 22,000 + P = 100,000
Subtract 22,000 from both sides:
4F + P = 78,000
Now a system of two equations:
P + F + 11,000 = 10V
4F + P = 78,000
solve this system of equations to find the values of F, P, and V.
By solving the system,
F = 7,000
P = 18,000
V = 4,000
Finally, substitute these values back into equation 1 to find the value of A:
A = F + 11,000 = 7,000 + 11,000 = 18,000
To know more about category here
https://brainly.com/question/31766837
#SPJ4
Sara walks at a constant speed. She walked 1 mile in 15 minutes. Which equation represents the amount of time in minutes, t, that it took for her to walk a distance of d miles? *
t = (1/15)d
t = 15d
t = d + 15
t = d - 15
Answers
Answer:
t=15d
Step-by-step explanation:
The problem is asking for total time, so we can set everything equal to t. If it takes 15 minutes for 1 mile and she's walking at a constant speed, we know that the solution is t=15d.
We can plug in one mile to verify this answer.
t=15(1)
t=15
Hope this helped!
Which graph represents a proportional relationship?

Answers
Is 4.887888 a rational number
Answers
Answer:
Step-by-step explanation:
yes it is
Anup bought 50 glasses
for Rs 1800
out of which 4 were broken. If
he sold the rest of the
glasses for Rs. 35 each. How much
profit or loss percentage did
he bear?
Answers
Step-by-step explanation:
50 glasses for Rs 1800
4 broken
sold each for Rs.35 each
50-4=46
35*46=1610
convert n = (2.80∠–29.9°) to rectangular form, (a + jb)
Answers
The rectangular form of n = (2.80∠–29.9°) is n = 2.45 – 1.38j.
To convert the polar form of n = (2.80∠–29.9°) to rectangular form, we can use the following equations:
a = r*cos(θ)
b = r*sin(θ)
where r is the magnitude of the complex number and θ is its angle in polar form.
Using the given values, we have:
r = 2.80
θ = –29.9°
Converting θ to radians:
θ = –29.9° * π/180 = –0.522 radians
Substituting the values in the equations, we get:
a = 2.80*cos(–0.522) = 2.45
b = 2.80*sin(–0.522) = –1.38
Therefore, the rectangular form of n = (2.80∠–29.9°) is:
n = 2.45 – 1.38j
So, The rectangular form of n = (2.80∠–29.9°) is n = 2.45 – 1.38j.
Learn more about rectangular form
brainly.com/question/11740879
#SPJ11