Name two sides that appear to be parallel
Answers
Step-by-step explanation:
These are sides that will never meet and are always the same distance apart. Some shapes that have parallel sides include the parallelogram, the rectangle, the square, the trapezoid, the hexagon, and the octagon.
Related Questions
what is the answer to this problem. solve x
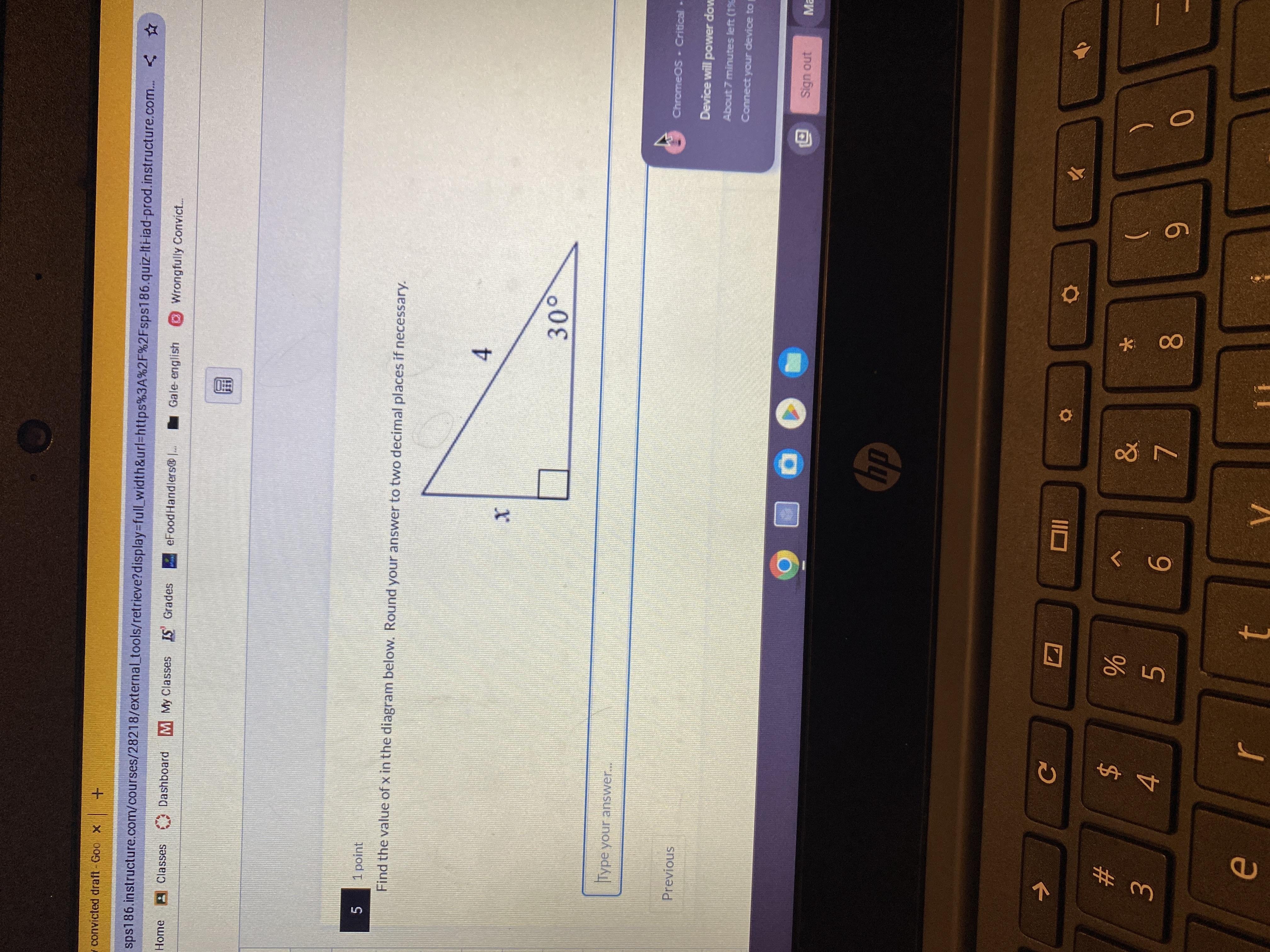
Answers
1/2=X/4
4/2=X
2=X
X=2

A country's population in 1990 was 154 million.
In 2001 it was 159 million. Estimate
the population in 2005 using the exponential
growth formula. Round your answer to the
nearest million.
P= Aekt
Answers
Using the exponential growth formula, the population in 2005 was 161 million.
The equation f(x) = a(1 + r)^x can also be used to compute exponential growth, where: The function is represented by the word f(x). The initial value of your data is represented by the a variable. The growth rate is represented by the r variable. To calculate growth rates, divide the difference between the starting and ending values for the period under study by the starting value.
Growth factor = (159/154) for the eleven-year period between 1990 and 2001.
The population growth might thus be described by the exponential equation
p(t) = 154(159/154)^(t/11), where t is the number of years since 1990.
The model forecasts a population of... p(15) = 154(159/154)^(15/11)
= 160.86 = 161 million
In 2005, there were about 161 million people living there.
Learn more about exponential growth formula Visit: brainly.com/question/27207350
#SPJ4
Correct Question:
A country's population in 1990 was 154 million. In 2001 it was 159 million. Estimate the population in 2005 using the exponential growth formula. Round your answer to the nearest million.
Plot 213, −56, and −312 on the number line.

Answers
Answer:
Step-by-step explanation:

Plot 213, −56, and −312 on the number line.
convert 400 km to miles
Answers
pharmaceutical company conducts an experiment in which a subject takes 75 mg of a substance orally. the researchers measure how many seconds it takes for one quarter of the substance to exit the bloodstream. what kind of variable is the company studying?
Answers
The pharmaceutical company uses the quantitative variable to conducts an experiment.
Variables:
A variable is a characteristic of an object. Their values may occur more than once for a set of data. We consider just two main types of variables in this course.
Quantitative Variables - Variables whose values result from counting or measuring something.
Qualitative Variables - Variables that are not measurement variables. Their values do not result from measuring or counting.
Given,
A pharmaceutical company conducts an experiment in which a subject takes 75 mg of a substance orally.
And the researchers measure how many seconds it takes for one quarter of the substance to exit the bloodstream.
Here we need to find the kind of variable is the company studying.
Here the company uses the Qualitative Variable because here they measure the effects of the medicine not the measurement.
So, the experiment uses the Qualitative Variable.
To know more about Variable here.
https://brainly.com/question/15078630
#SPJ4
A child's weight (lbs) can be expressed as the function f(x)= 0.5x + 7.8. where x is time in months. How much did the
child weigh when it was born?
Answers
On solving the provided question, we can say that - the of the function f(x) = 0.5x + 7.8 = 9.8
what is function?The topic of numbers, formulae and associated structures, forms and the areas where they exist, quantities and their variations, and spaces where they exist are all included in the field of mathematics. An association between a collection of inputs, each of which has an output, is known as a function. A function is, to put it simply, a relationship between inputs and outputs, where each input has a single, specific outcome. A domain and a codomain, or scope, are assigned to each function. Typically, f is used to represent functions (x). input is x. Four different sorts of functions are available. Based on the following items: One-to-one functions, many-to-one functions, on functions, one-to-one functions, and within functions.
here, we are provided with the function -
f(x)= 0.5x + 7.8
and given from question, x = 4
f(x) = 2 + 7.8 = 9.8
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
What is the inverse of the function f(x) = one-quarterx – 12?
Answers
Answer:
f^(-1)(x) = 4x + 48.
Step-by-step explanation:
Is suppose the function is f(x) = 1/4 x - 12
This is equivalent to the line y = 1/4 x - 12.
To get the inverse, change the x and y:
x = 1/4 y - 12
Now solve for y:
x + 12 = 1/4 y
y = 4x + 48
So the inverse f^(-1)(x) = 4x + 48.
Answer:
f-1(x) = 4x + 48.
Step-by-step explanation:
let f(x) = y = 1/4 x - 12
We solve for x:
y = 1/4 x - 12
1/4 x = y +12
Multiply through by 4:
x = 4y + 48
The inverse f-1(x) = 4x + 48.
Determine whether the equation below has a one solutions, no solutions, or an
infinite number of solutions. Afterwards, determine two values of x that support your
conclusion
2 + 6 = 9
The equation has infinite solutions
A value of x that makes the equation true is
3
which when substituted into the
equation and simplified makes the equation turn into
х
3
Another value of x that makes the equation true is -15 , which when substituted
into the equation and simplified makes the equation turn into 3
= - 15

Answers
Do you guys know the answer I got to get a good grade on this test pls help guys

Answers
Answer: The slope should be the first one. 1/4
Hope this helps <3.
Before 8 A.M., there were 64 trucks and 24 cars in a parking lot. Between 8 A.M. and 9 A.M., more cars entered the parking lot and no trucks entered or exited the lot. At 9:00 A.M., the number of trucks represented 1/5 of the parking lot's vehicles. How many cars entered between 8 A.M. and 9 A.M? A. 56 B. 112 C. 148 D. 192 PLZ EXPLAIN
Answers
Answer:
232 cars
Step-by-step explanation:
Let's say the number of cars that entered is c.
At 9:00 am, there are a total of 24 + c cars and 64 trucks. We know that this value of 64 represents 1/5 of the total number of vehicles. The total number of vehicles is (24 + c) + 64 = 88 + c. So, we have:
64/(88 + c) = 1/5
Cross-multiply:
88 + c = 64 * 5 = 320
c = 320 - 88 = 232
Thus, the answer is 232 cars.
Note: as 232 doesn't show up in the answer choices, it's possible that the problem was copied correctly.
~ an aesthetics lover
Answer:
232 cars entered between 8 and 9
Step-by-step explanation:
at 9 am there are 64 x 5 vehicles total = 320
320 - 64 - 24 = 232
Find the measure of each angle in the figure below.

Answers
Answer:
a=90
b=45
c=45
d=90
e=45
f=45
What set of reflections would carry trapezoid ABCD onto itself? (1 point) Trapezoid ABCD is shown. A is at negative 5, 1. B is at negative 4, 3. C is at negative 2, 3. D is at negative 1, 1. Group of answer choices x-axis, y=x, y-axis, x-axis x-axis, y-axis, x-axis y=x, x-axis, x-axis y-axis, x-axis, y-axis, x-axis
Answers
Answer:
y=x, x axis, y=x, y axis
Step-by-step explanation:
If a point A(x, y) is reflected along the y = x line, the new coordinates would be A'(y, x)
If a point A(x, y) is reflected across the x axis, the new coordinates would be A'(x, -y)
If a point A(x, y) is reflected along the y axis, the new coordinates would be A'(-x, y)
Firstly reflect Trapezoid ABCD along the y = x line to give:
A (-5, 1) ⇒ A'(1, -5). B (-4, 3) ⇒ B'(3, -4). C (-2, 3) ⇒C'(3, -2). D (-1, 1) ⇒ D'(1, -1)
Secondly reflect along the x axis to give:
A'(1, -5)⇒ A"(1,5). B'(3, -4)⇒ B"(3,4), C'(3, -2)⇒C"(3, 2), D'(1, -1) ⇒ D"(1, 1)
Thirdly reflect along the y = x line to give:
A"(1,5) ⇒ A"'(5, 1). B"(3,4) ⇒ B"'(4, 3). C"(3, 2) ⇒ C"'(2, 3). D"(1, 1) ⇒ D"'(1, 1)
Lastly reflect along the y axis to give:
A"'(5, 1) ⇒ A""(-5, 1), B"'(4, 3) ⇒ B""(-4, 3), C"'(2, 3) ⇒ C""(-2, 3), D"'(1, 1) ⇒ D""(-1.1)
Answer:
y-axis, x-axis, y-axis, x-axis
Sorry for being really late but i hope this helps someone out there. I took the test and that was the correct answer.
states visited in a two week political campaign at a rate of 2 states per day
Answers
Answer:
I'm confused on what you are asking here.
Step-by-step explanation:
If we are told that ab= 0, then what can we infer by the zero product property we know =0 or. =0
Answers
When ab = 0, the zero-product property tells us that at least one of the factors (a or b) must be zero in order for the equation to hold true.
We are given that ab = 0, where a and b are variables or numbers.
According to the zero-product property, if the product of two factors is equal to zero, then at least one of the factors must be zero.
In our case, we have ab = 0. This means that the product of a and b is equal to zero.
To satisfy the condition ab = 0, at least one of the factors (a or b) must be zero. If either a or b is zero, then when multiplied with the other factor, the product will be zero.
It is also possible for both a and b to be zero, as anything multiplied by zero gives zero.
Therefore, based on the zero-product property, we can infer that either a = 0 or b = 0 when ab = 0.
In summary, when ab = 0, the zero-product property tells us that at least one of the factors (a or b) must be zero in order for the equation to hold true.
Learn more about property from
https://brainly.com/question/2807928
#SPJ11
find the box's speed vf at 2.6 s after you first started pushing on it.
Answers
The box's speed vf at 2.6 seconds after you first started pushing it is 18.2 m/s.
To determine the box's speed vf at 2.6 seconds after you first started pushing it, we first need to find the acceleration of the box and then use that acceleration to calculate its velocity using the kinematic equation:
v_f = v_i + at
Where:
v_f is the final velocity of the box
v_i is the initial velocity of the boxa is the acceleration
t is the time
First, we can use the given information to find the acceleration of the box using the equation:
a = F / m
Where:
F is the force you applied to the boxm is the mass of the box
From the given values, we have:
F = 35 Nm = 5 kg
Substituting these values into the equation above, we get:a = 35 N / 5 kga = 7 m/s^2
Now that we have the acceleration of the box, we can use the kinematic equation above to find its final velocity:v_f = v_i + at
We are given that the box starts from rest (v_i = 0).
Substituting the values we have so far, we get:
v_f = 0 + (7 m/s^2) × (2.6 s)v_f = 18.2 m/s
Learn more about velocity at:
https://brainly.com/question/29110878
#SPJ11
It’s confusing on how they worded it to me
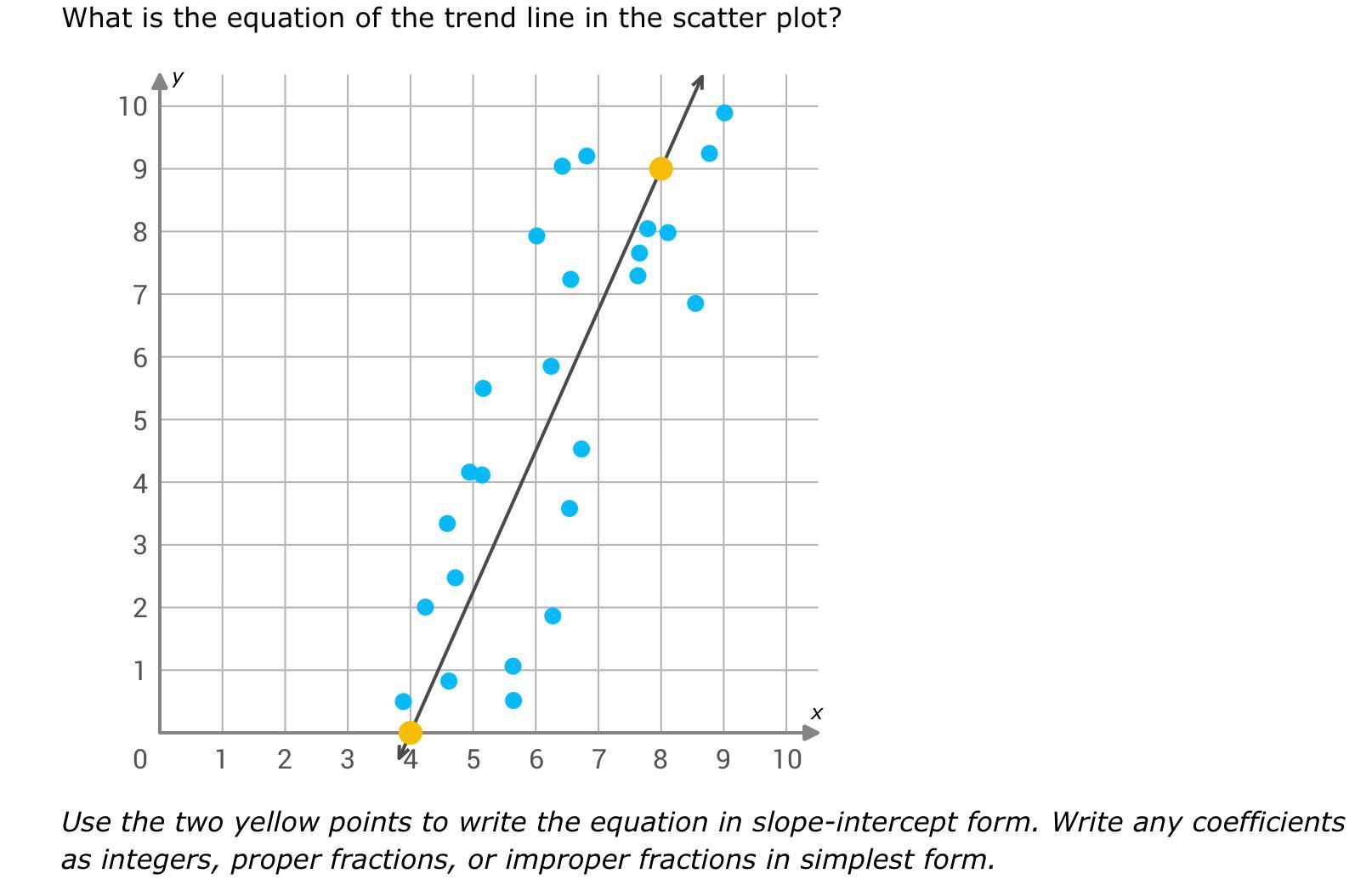
Answers
You're looking for the equation of the line through the two yellow points, whose coordinates are (4, 0) and (8, 9).
Compute the slope:
(9 - 0) / (8 - 4) = 9/4
Using the point-slope formula, the equation of the line is
y - 0 = 9/4 (x - 4)
or
y = 9x/4 - 9
What is the approximate area of the shaded sector in the circle shown below

Answers
Answer: B
Step-by-step explanation:
The area of a circle is pi*radius^2. But only a diameter is given, so in order to find the radius, you must divide the diameter by 2:
3.6/2 = 1.8
Now, you can plug the radius, 1.8, into the equation pi*radius^2 (\(\pi r^{2}\)):
\(\pi (1.8)^2 = \pi(3.24)\) = about 10.18
Lastly, you must divide the area 10.18 by 2 because you are looking for only half the area.
10.18/2 = 5.09
The area of the shaded region is 5.09 square cm if the radius of the circle is 1.8 cm, option (B) is correct.
What is a circle?It is described as a set of points, where each point is at the same distance from a fixed point (called the centre of a circle)
We have:
The diameter of the circle = 3.6 cm
The radius of the circle = 3.6/2 = 1.8 cm
Area of shaded region = (180/360)π(1.8)²
Area of the shaded region = 5.089 ≈ 5.09 square cm
Thus, the area of the shaded region is 5.09 square cm if the radius of the circle is 1.8 cm, option (B) is correct.
Learn more about circle here:
brainly.com/question/11833983
#SPJ5
Please explain it with EVERY step.

Answers
6, 30, and another number are all factors of 270.
270/4 = 67.5
270/18 = 15
270/24 = 11.25
270/180 = 1.5
As you can see, 18 goes into 270 perfectly 15 times.
How to do 3 digit subtraction with regrouping?
Answers
Answer:
7 13
283
+ 167
--------
116
Step-by-step explanation
on a standard 6-sided die, what is the probability of rolling a 5?
Answers
Answer:
1/6
Step-by-step explanation:
Kroger sells peaches for 1.20 a pound if joe bought 2 1/2 pounds of peaches how much did he spend
Answers
Answer:
Joe spent $3 on peaches
Step-by-step explanation:
I need help with this question please

Answers
Answer:The correct answer is A
Step-by-step explanation: just trust me
Periodic Deposit: $? at the end of each monthRate: 7.5% compounded monthlyTime: 3 yearsFinancial Goal: $35,000O A. $2,628; $31,536 from deposits and $3,464 from interestB. $776; $27,936 from deposits and $7,064 from interestO c. $933; $33,588 from deposits and $1,412 from interestOD. $870; $31,320 from deposits and $3,680 from interest

Answers
Answer:
D. $870; $31,320 from deposits and $3,680 from interest
Explanation:
In order to calculate the monthly payment, we use the formula below:
\(P=\frac{A\mleft(\frac{r}{n}\mright)}{\mleft[\mleft(1+\frac{r}{n}\mright)^{nt}-1\mright]}\)Given:
• The Financial Goal, A= $35,000
,• Rate = 7.5% = 0.075
,• Number of compounding period = 12 (Monthly)
,• Time, t = 3 years
Substitute into the given formula:
\(\begin{gathered} P=\frac{35000\mleft(\frac{0.075}{12}\mright)}{\mleft[\mleft(1+\frac{0.075}{12}\mright)^{12\times3}-1\mright]} \\ P\approx\$870 \end{gathered}\)The monthly payment is $870.
\(\begin{gathered} \text{Total deposit}=870\times36=31,320 \\ \text{Interests}=35,000-31,320=3680 \end{gathered}\)Option D is correct.
Examples: Solving One-Step
Equations:
1. X + 2 = 7
Answers
Answer:
5
.......
...................
..
which of the following rational functions is graphed below

Answers
Answer:
D.
Step-by-step explanation:
The simplest and fastest way to answer this question is to graph the equations given. Once you do so, then you should see that D is the correct answer.
Dali runs three times as fast as he walks. In the morning he goes to school. He walks half the distance and runs half the distance, taking 24 minutes altogether. After school he goes home. He walks half the time and runs half the time. How many minutes does it take Dali to get home?
Answers
Let's say Dali's walking speed is x and his running speed is 3x.
In the morning, let's say the total distance is d. Therefore, Dali walks d/2 with speed x and runs d/2 with speed 3x. The time it takes for him to complete this distance is given by:
d/2x + d/2(3x) = 24
Simplifying this equation, we get:
d = 3x(8)
d = 24x
So, the total distance Dali covers in the morning is 24x.
After school, let's say the distance from school to home is d'. Therefore, Dali walks d'/2 with speed x and runs d'/2 with speed 3x. The time it takes for him to complete this distance is given by:
d'/2x + d'/2(3x) = ?
We don't know how much time it takes Dali to get home, so we'll leave the right-hand side of the equation blank for now.
Now, let's look at the ratios of Dali's walking and running speeds:
Walking speed : Running speed = x : 3x = 1 : 3
This means that for every 4 parts of the distance Dali covers, he walks one part and runs three parts. So, we can write:
d' = 4y, where y is the distance Dali walks
This also means that Dali spends one-fourth of the total time walking and three-fourths running. So, we can write:
d'/2x + d'/2(3x) = (1/4)t + (3/4)t, where t is the total time it takes Dali to get home
Simplifying this equation, we get:
2d' = 2t(x + 3x)
4y = 8tx
y = 2tx
Substituting this value of y in the equation d' = 4y, we get:
d' = 8tx
So, the total distance Dali covers in the afternoon is 8tx.
Now, we have two equations:
d = 24x
d' = 8tx
We need to simplify these equations further to find the value of t (the total time it takes Dali to get home).
From the first equation, we get:
x = d/24
Substituting this value of x in the second equation, we get:
d' = 8t(d/24)
d' = (1/3)dt
So, the total distance Dali covers in the afternoon is (1/3)dt.
Now, we can equate the two expressions we have for d':
d' = 8tx = (1/3)dt
Simplifying this equation, we get:
24x = t
Therefore, it takes Dali 24 minutes to get home.
The principal P is borrowed at a simple interest rate r for a period of time t. Find the loan's future value A, or the total amount due at time t. P = $20,000, r = 5.5%
Answers
the loan's future value or the total amount due at time t is $23,300 if the loan is borrowed at a simple interest rate of 5.5% for a period of 3 years.
The principal P is borrowed at a simple interest rate r for a period of time t. Find the loan's future value A, or the total amount due at time t. P = $20,000, r = 5.5%
The formula for calculating the future value of a simple interest loan is:
FV = P(1 + rt)
where FV represents the future value, P is the principal, r is the interest rate, and t is the time in years. Therefore, using the given values: P = $20,000 and r = 5.5% (or 0.055) and the fact that no time is given, we cannot determine the exact future value.
However, we can find the future value for different periods of time. For example, if the time period is 3 years:
FV = $20,000(1 + 0.055 × 3) = $20,000(1.165) = $23,300
Therefore, the loan's future value or the total amount due at time t is $23,300 if the loan is borrowed at a simple interest rate of 5.5% for a period of 3 years.
learn more about interest rate here
https://brainly.com/question/25720319
#SPJ11
flight time from london to chicago can be classified as________ data continious discrete independent variable dependent variable
Answers
Time is a continuous data type, meaning it can take any value within a range. For example, the flight time from London to Chicago could range from 6 to 8 hours.
Continuous data is a type of data that can take any value within a range. As opposed to discrete data which can only take certain values, continuous data can take any value within a range. An example of continuous data is time. The flight time from London to Chicago could range from 6 to 8 hours. This time can be measured in any unit, such as seconds, minutes, hours, or days. This type of data is useful in many fields such as mathematics, engineering, and economics. Continuous data provides a more accurate representation of real-world phenomena that often follow a certain pattern or trend. This type of data is also important for analyzing relationships between variables and for making predictions about the future.
Learn more about data here
https://brainly.com/question/14893265
#SPJ4
30 IS 15% of WHAT number?
A. 333.3
B. 266.6
C. 600
D. 200
Answers
Answer:
The correct answer is D) 200
Step by step explanation:
Let x be the number:
Then,
→15/100(x)=30
→3/20(x)=30
→3x/20=30
→3x=20⋅30
→3x=600
→x=600/3=200
Hope it helps!
Answer:
D 200
Step-by-step explanation:
Let the number we are find be x. We can write this as an equation:
30 = 15%*x = (15/100)x
Multiplying by 100/15 on both sides to isolate x:
x = 30(100/15) = 2(100) = 200
Therefore, 200 is our answer. I hope this helps! :)
very fast
Show, by induction, that \( T(n)=10 n^{2}-3 n \quad \) if \( n=1 \)
Answers
Given that \(\(T(n)\) = \(10n^2-3n\)\) if (\(\(n=1\)\)), you have to prove it by induction. So, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if ( n= 1). The given statement is true for all positive integers n
Let's do it below: The base case (n=1) is given as follows: \(T(1)\) =\(10\cdot 1^2-3\cdot 1\\&\)=\(7\end{aligned}$$\). This implies that \(\(T(1)\)\) holds true for the base case.
Now, let's assume that \(\(T(k)=10k^2-3k\)\) holds true for some arbitrary \(\(k\geq 1\).\)
Thus, for n=k+1, T(k+1) = \(10(k+1)^2-3(k+1)\\&\) = \(10(k^2+2k+1)-3k-3\\&\)=\(10k^2+20k+7k+7\\&\) = \(10k^2-3k+20k+7k+7\\&\) = \(T(k)+23k+7\\&\) = \((10k^2-3k)+23k+7\\&\) = \(10(k+1)^2-3(k+1)\).
Therefore, we have proved that the statement holds true for n=k+1 as well. Hence, we have proved it by induction that \($$\(T(n)=10n^2-3n\)$$\) if (n=1). Therefore, the given statement is true for all positive integers n.
For more questions on: integers
https://brainly.com/question/17695139
#SPJ8