Answers
Answer: The middle school has 652 students.
Step-by-step explanation: Divide the number of student in the high school by 4.5
\(\frac{2934}{4.5}\) = 652
Related Questions
Q is a degree 5 polynomial that passes through the origin, has zeros i and 7 - i, and q(-1)= -520. find the equation for q
Answers
Using the factor theorem, the equation for q is:
\(q(x) = 4(x^5 - 14x^4 + 51x^3 - 14x^2 + 50x)\)
The Factor Theorem states that a polynomial function with roots \(x_1, x_2, ..., x_n\) is given by:
\(f(x) = a(x - x_1)(x - x_2)...(x - x_n)\)
In which a is the leading coefficient.
In this problem:
Passes through the origin, so x = 0 is a zero, that is \(x_1 = 0\).x = i is a zero, and thus, it's conjugate also is, that is, x = -i, hence \(x_2 = i, x_3 = -i\)x = 7 - i is a zero, and thus, it's conjugate also is, that is, x = 7 + i, hence \(x_4 = 7 - i, x_3 = 7 + i\)Then, the equation is:
\(q(x) = a(x - 0)(x - i)(x + i)(x - 7 + i)(x - 7 - i)\)
\(q(x) = ax(x^2 - i^2)((x-7)^2 - i^2)\)
Considering that \(i^2 = -1\)
\(q(x) = ax(x^2 + 1)(x^2 - 14x + 50)\)
\(q(x) = ax(x^4 - 14x^3 + 51x^2 - 14x + 50)\)
\(q(x) = a(x^5 - 14x^4 + 51x^3 - 14x^2 + 50x)\)
q(-1) = -520 means that when \(x = -1, q = -520\), and this is used to find a.
\(q(x) = a(x^5 - 14x^4 + 51x^3 - 14x^2 + 50x)\)
\(-520 = a(-1 - 14 - 51 - 14 - 50)\)
\(130a = 520\)
\(a = \frac{520}{130}\)
\(a = 4\)
Hence, the equation is:
\(q(x) = 4(x^5 - 14x^4 + 51x^3 - 14x^2 + 50x)\)
A similar problem is given at https://brainly.com/question/24380382
Pls help i need this by the end of today

Answers
The average rate of change of the total cost as his shirt production increases from 10 to 20 is 150.
What is the average rate of change?The Average Rate of Change function is defined as the average rate at which one quantity is changing with respect to something else changing.
Given that, the total cost to produce by James shirts is represented by a function, f(x) = 5x²+6.
We are to find the average rate of change of the total cost as his shirt production increases from 10 to 20.
The average rate of change is given by =
f(b) - f(a) / b-a, where a and b are given intervals,
Here, we have, a = 10 and b = 20
f(b) = 5(20)²+6 = 2006
f(a) = 5(10)²+6 = 506
The rate of change =
2006 - 506 / 20-10
= 1500 / 10
= 150
Hence, the average rate of change of the total cost as his shirt production increases from 10 to 20 is 150.
Learn more about average rate of change, click;
https://brainly.com/question/23715190
#SPJ1
5c + 4 = 2(0 - 5)
.
Answers
Answer: c=−14/5
Step-by-step explanation: Hope this help

Answer:
c = -2 4/5
Step-by-step explanation:
5c + 4 = 2(0 - 5)
Parentheses first
5c + 4 = 2(-5)
5c +4 = -10
Subtract 4 from each side
5c+4-4 = -10-4
5c = -14
Divide by 5
5c/5 = -14/5
c = -14/5
c = -2 4/5
find the area of each triangle. Round intermediate values to the nearest tenth. use the rounded values to calculate the next value. Round your final answer to the nearest tenth, someone help me pelaseeeee!!!!

Answers
Answer:
54? or 5.4 I not really sure but I tried my best
which property of equality should you use to solve the equation for x? -3x = 21
A. The division property of equality
B. The subtraction property of equality
C. The addition property of equality
D. The multiplication property of equality
Answers
Answer:
A. The division property of equality
Step-by-step explanation:
To get x you need to find a way to get it by itself, which can be done by dividing -3 from both sides of the equation (which is the division property of equality).
For example,
-3x=21
/-3 /-3
x=21/-3
x=-7
-2(t+-4)=10-2t how many solutions does this equation have.
Answers
the given expression is
-2 (t + (-4) ) = 10 -2t
= -2t + 8 = 10 - 2t
In slope-intercept form, what is the equation of the line passing through the points (2,13)and (5,22)
Answers
Answer:
y = 3x + 7
Step-by-step explanation:
As we move from (2, 13) to (5, 22), x (the "run") increases by 3 and y (the "rise") increases by 9. Thus, the slope, m, must be m = rise / run = 9/3, or 3.
Then we have y = 3x + b and must find b. Subbing 2 for x and 13 for y, we get
13 = 3(2) + b, so that b must be 7.
The desired equation is y = 3x + 7.
The data below shows the grams of fat in a series of popular snacks. snack grams of fat snack 1 9 snack 2 13 snack 3 21 snack 4 30 snack 5 31 snack 6 31 snack 7 34 snack 8 25 snack 9 28 snack 10 20 if morris wanted to construct a one-sample t-statistic, what would the value for the degrees of freedom be?
Answers
The value for the degrees of freedom in Morris's one-sample t-statistic would be 9.
To calculate the degrees of freedom for a one-sample t-statistic,
we need to consider the sample size.
In this case, the sample size is 10, representing the number of snacks in the data set.
Degrees of freedom (df) for a one-sample t-test is given by the formula:
df = n - 1
where "n" is the sample size.
In this case, the sample size is 10,
so the degrees of freedom would be:
df = 10 - 1 = 9
Learn more about Degrees of freedom here:
https://brainly.com/question/32093315
#SPJ11
A basketball coach is treating her team to
lunch. Each meal costs $7.25. If the coach
plans on purchasing 15 meals and there is a
5% sales tax, how much will the coach's total
be?
Answers
Answer: The cost of 15 meals at $7.25 per meal is:
15 x $7.25 = $108.75
To find the cost including the 5% sales tax, we need to add 5% of the cost to the cost:
5% of $108.75 = 0.05 x $108.75 = $5.44
So the total cost, including the sales tax, is:
$108.75 + $5.44 = $114.19
Therefore, the coach's total cost for 15 meals, including sales tax, will be $114.19.
Express the ratio below in its simplest form
12:6
Answers
Answer:
12/6 simplified to lowest terms is 2/1.
Step-by-step explanation:
Divide both the numerator and denominator by the HCF
12 ÷ 6
6 ÷ 6
Reduced fraction:
12/6 simplified to lowest terms is 2/1.
Answer: 2:1
Step-by-step explanation:
12:6
Both left and right can be divided by 6, like a fraction, reduce.
= 2:1
y=2/x-3/x^2 find the tangent line at (1,-1)
Answers
Answer:
To find the equation of the tangent line at the point (1,-1), we need to find the derivative of the function y=2/x-3/x^2 first.
y = 2/x - 3/x^2
y' = -2/x^2 + 6/x^3
Now we can plug in x=1 to find the slope of the tangent line at (1,-1).
y'(1) = -2/1^2 + 6/1^3 = 4
So the slope of the tangent line is 4.
To find the equation of the tangent line, we can use the point-slope form:
y - y1 = m(x - x1)
where m is the slope and (x1,y1) is the point (1,-1).
Plugging in the values, we get:
y - (-1) = 4(x - 1)
Simplifying, we get:
y = 4x - 5
Therefore, the equation of the tangent line at (1,-1) is y=4x-5.
Step-by-step explanation:
5. In any metric space (M,D), prove that D(a 1 ,an )≤D(a1 ,a 2 )+ D(a ,a 3 )+⋯+D(a n−1 ,a n ), for a 1 ,a ,…,an ∈M. 1
Answers
D(a₁, an) ≤ D(a₁, a₂) + D(a₂, a₃) + ⋯ + D(aₙ₋₁, aₙ) for any metric space (M, D) and elements a₁, a₂, ..., aₙ ∈ M.
To prove the inequality D(a₁, an) ≤ D(a₁, a₂) + D(a₂, a₃) + ⋯ + D(aₙ₋₁, aₙ) for any metric space (M, D) and elements a₁, a₂, ..., aₙ ∈ M, we can use the triangle inequality property of a metric space.
The triangle inequality states that for any three points x, y, and z in a metric space, the distance between x and z is always less than or equal to the sum of the distances between x and y, and between y and z. Mathematically, it can be written as:
D(x, z) ≤ D(x, y) + D(y, z)
Now, let's consider the elements a₁, a₂, ..., aₙ ∈ M.
By applying the triangle inequality repeatedly, we can write:
D(a₁, aₙ) ≤ D(a₁, a₂) + D(a₂, a₃) + ... + D(aₙ₋₁, aₙ)
This inequality holds because we can view the distance between a₁ and aₙ as the sum of the distances between adjacent points in the sequence a₁, a₂, ..., aₙ.
Therefore, we have proved that D(a₁, an) ≤ D(a₁, a₂) + D(a₂, a₃) + ⋯ + D(aₙ₋₁, aₙ) for any metric space (M, D) and elements a₁, a₂, ..., aₙ ∈ M.
Learn more about Metric space here
https://brainly.com/question/32645192
#SPJ11
12 cookies divided among 9 people equation form
Answers
Answer:
9x =27
Step-by-step explanation:
And the solution is shown in the image I shared
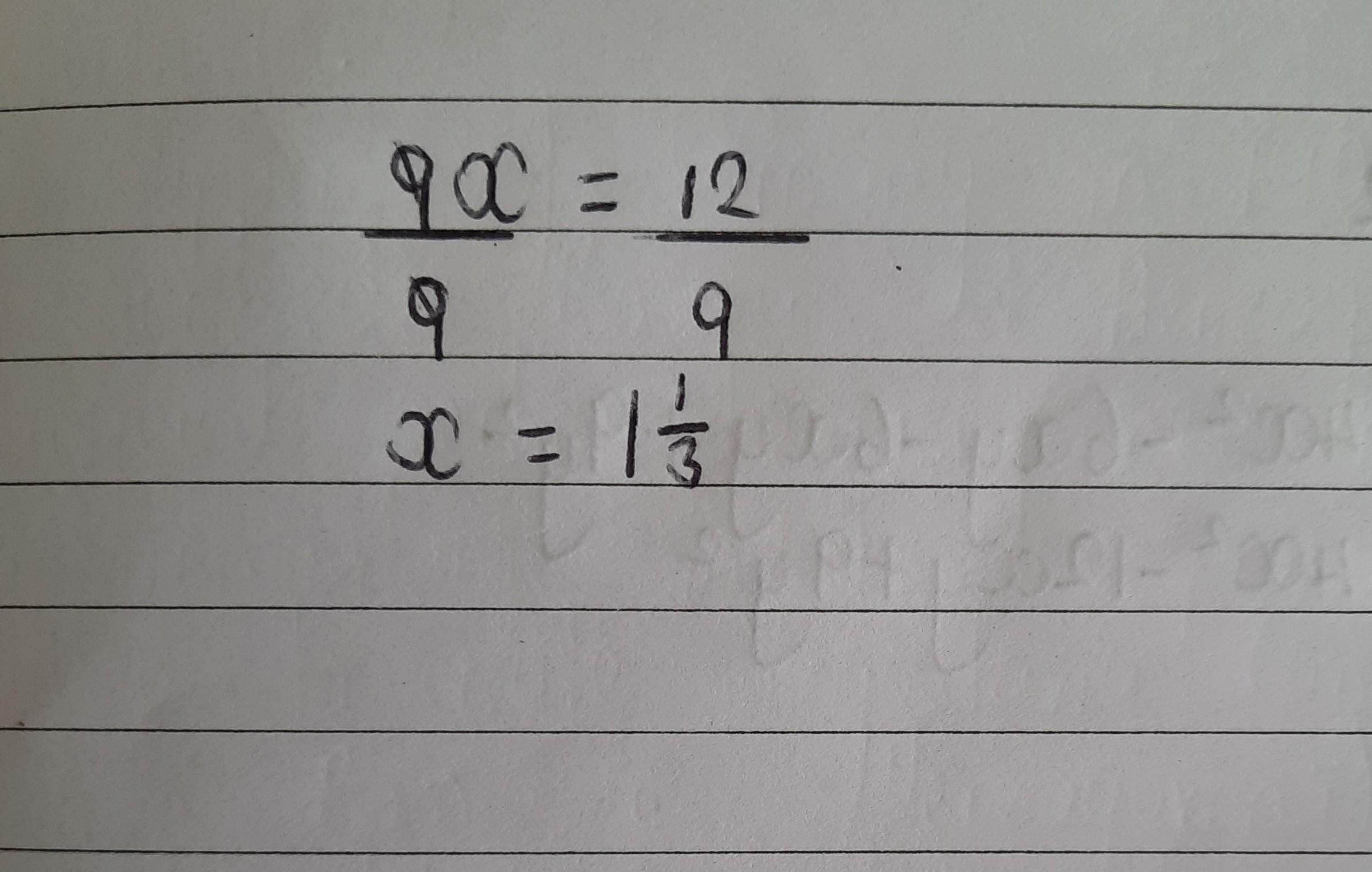
Find the slope of the tangent line to the parabola at the point.
Answers
The equation of the tangent line to the parabola at the point (1,5) is y = 4x + 1.
To find the slope of the tangent line to the parabola at the point (1,5), we need to find the derivative of the equation y = 6x - x² and evaluate it at x = 1.
Taking the derivative of y with respect to x:
dy/dx = d(6x - x²)/dx
= 6 - 2x
Now, we can substitute x = 1 into the derivative to find the slope at that point:
slope = 6 - 2(1)
= 6 - 2
= 4
So, the slope of the tangent line to the parabola at the point (1,5) is 4.
To find the equation of the tangent line, we need to use the point-slope form of a line.
The equation is given by:
y - y₁ = m(x - x₁)
Substituting the values we have:
y - 5 = 4(x - 1)
Expanding and simplifying:
y - 5 = 4x - 4
Moving the constant term to the other side:
y = 4x + 1
Therefore, the equation of the tangent line to the parabola at the point (1,5) is y = 4x + 1.
Learn more about tangent line click;
https://brainly.com/question/23416900
#SPJ4
Complete question =
Find the slope of the tangent line to the parabola at the point (1,5). y = 6x-x². find an equation of the tangent line.

exercise 5.3.1. recall from exercise 4.4.9 that a function f : a → r is lipschitz on a if there exists an m > 0 such that ∣∣∣∣ f(x) − f(y) x − y ∣∣∣∣ ≤ m for all x ?
Answers
If f is differentiable on a closed interval [a,b] and if f' is continuous on the interval [a,b], Then f is Lipschitz on [a,b].
What is a Lipschitz function?
If a neighborhood U of x exists for any x in X such that f restricted to U is Lipschitz continuous, then the function is said to be locally Lipschitz continuous. Alternatively, f is locally Lipschitz if and only if it is Lipschitz continuous on each compact subset of X if X is a locally compact metric space.
Now,
Assume that f can be differentiated and that f' is continuous on [a,b]. Therefore, f' is bounded since [a,b] is compact. In other words, for all x [a,b] there exists M > 0 such that: |f'(x)| ≤ M.The Mean Value Theorem therefore ensures that there exists c between x and y such that: \(|\frac{f(x)-f(y)}{x-y}|=|f'(c)|\leq M\), for each x,y ∈[a,b].Given that x and y were chosen at random, we can infer that f is Lipschitz on [a,b] since the inequality: \(|\frac{f(x)-f(y)}{x-y}|\leq M\), holds for all x,y ∈ [a,b].Hence, If f is differentiable on a closed interval [a,b] and if f' is continuous on the interval [a,b], Then f is Lipschitz on [a,b].
To learn more about Lipschitz function, refer to the link: https://brainly.com/textbook-solutions/q-22-expand-equation-f-x-x-4
#SPJ4
Jamal asks his friend Sam, "How many days are in December?" Is this a statistical question? Why or why not?
Answers
Answer:
in total there are seven months with 31 days which means there are 31 days in december. It starts on the same weekday as September and ends on the same weekday as april every year.
This would not be a statistical question because it does not have varying data. An example would be: What is the typical number of pets owned by students in my class.
Jim is mailing packages. Each small package costs him $3.20 to send. Each large costs him $4.70. How much will it cost him to send 1 small package and 4 large packages?
Answers
Answer:
$3.20 for the small and $4.70 for the large packages.
Step-by-step explanation:
multiply 3.20 by 1 since that is the price of mailing a small package and you want to mail 1.
multiply 4.70 by 4 since that is the price of a large one and you want to mail 4.
3.20 x 1 =3.20
4.70 x 4=18.80
Determine the relationship between the two triangles and whether or not they ca
proven to be
can be
congruent.

Answers
Answer:
They are congruent.
Step-by-step explanation:
The have the same side length, as shown by the marking on the side next to the double marked angle and across from single marked angle. They have the same angle measures located in the same places as well. They are congruent as proven by shape, angle measures, and side length.
question math genius help but preparation for tmrw math exam
a) 2x-y-3=0,4x+y-3=0
lots of thx if u helped
Answers
Step-by-step explanation:
make sure to number your equations
\(2x - y - 3 = 0 \: \: \: \: \: \: \: \: \: \: \: (1)\)
\(4x + y - 3 = 0 \: \: \: \: \: \: \: \: \: \: \: \: \: (2)\)
In equation 2 make y the subject
\(y = - 4x + 3 \: \: \: \: \: \: \: \: \: (3)\)
subs 3 into 1
\(2x - ( - 4x + 3) - 3 = 0\)
\(2x + 4x - 3 - 3 = 0\)
\(6x - 6 = 0\)
\(6x = 6\)
\(x = 1 \: \: \: \: \: \: \: \: \: \: \: (4)\)
sub's 4 into 2
\(4(1) + y - 3 = 0\)
\(4 + y - 3 = 0\)
\(y = - 4 + 3\)
\(y = - 1\)
Fill in the blan
points
Given: ABCD is a parallelogram.
Prove: AABD ACDB.
A
D
Statements
Reasons
1. ABCD is a parallelogram.
1.
Given
2.4A 24C
2.
????

Answers
Answer:
Screenshot the answer choices I don't remember them right off rip
Step-by-step explanation:
I can buy 4 basketballs for $44. At that same rate, how much would 8 basketballs cost?
Answers
Answer:
$88.
Step-by-step explanation:
$44 dollar for 4 balls.
That means for one ball it is $11.
44 ÷ 4 = 11.
Therefore:
8 x 11 = 88.
The answer is $88.
Hope this helps!
if 4 basketballs cost $44 then you could do 4 times 11 equals 44
therefore do 8 times 11
$88
i need help does anyone know this question

Answers
Answer:
The third answer is correct.
Step-by-step explanation:
You are going to translate the smaller quadrilateral (4 sided figure) to the larger quadrilateral. Then you need the scale factor from the smaller figure to the larger.
Side EF times the scale factor will give you side AB. Let's call the scale factor s then our equation would be:
EF x s = AB To find s divide both sides by EF
\(\frac{EF(s)}{EF}\) = \(\frac{AB}{EF}\)
s = \(\frac{AB}{EF}\) This is our scale factor.
Helping in the name of Jesus.
Which values are areas of cross sections that are parallel to a face of this right rectangular prism?
480 square units
120 square units
80 square units
24 square units
Answers
The value is 24 square units is parallel to the face of the right rectangular prism.
We can see that the face of the given rectangular prism shows a width 4 and a height of 6. If we cut the figure at any point along the length 20, such that the cross-section is parallel to the face, the cross-section, which occurs at x length, will always have the same dimensions, which are 4 and 6.
So the area of the cross-section which is parallel to the face of the given rectangular prism is given by:
A = 6 × 4
A = 24
Thus, the value is 24 square units is parallel to the face of the right rectangular prism.
To know more about prism visit: brainly.com/question/21308574
#SPJ4
A = 6 × 4
A = 24
Thus, the value is 24 square units is parallel to the face of the right rectangular prism.
Evaluate this exponential expression.
A. 63
OB. 66
C. 19
D. 207
6 (4+2)2-32
Answers
Answer:To evaluate the exponential expression 6(4+2)² - 32, we need to follow the order of operations, which is parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
First, we simplify the expression inside the parentheses:
4 + 2 = 6
Next, we square the result:
6² = 36
Now, we substitute the squared result back into the expression:
6(36) - 32
Next, we perform the multiplication:
6 * 36 = 216
Finally, we subtract 32:
216 - 32 = 184
Therefore, the value of the given exponential expression 6(4+2)² - 32 is 184.
Peyton buys cookies and apples at the store.
She pays a total of $51.26.
She pays a total of $6.54 for the cookies.
She buys 8 bags of apples that each cost the same amount.
Write and solve an equation which can be used to determine
x
x, how much each bag of apples costs.
I need an answer please
Answers
Answer:
Hope this helps sorry I'm in class right now
Step-by-step explanation:

The diagram shows an open rectangular box ABCDEFGH.
A straight stick AGM rests against A and G and extends outside the box to M.
a. Calculate the angle between the stick and the base of the box.
b. AM= 30 cm.
Show that GM= 4.8 cm, correct
to 1 decimal place.

Answers
The angle between the stick and the base of the box is 77. 9 degrees
How to determine the angleTo determine the angle between the stick and the base, we have to know the trigonometric identities.
These identities are;
sinecosinecotangenttangentsecantcosecantFrom the information given, we have;
sin A = FB/AB
Given that;
GB = 14.5cm
AB = 18. 6cm
substitute for the length of the sides, we have;
sin A = 14.5/18. 6
Divide the values, we have;
sin A = 0. 7796
Find the inverse sine
A = 77. 9 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
Your son is starting at a prep school and will need to wear a shirt and tie every day. In his closet he has 4 blue shirts, 3 plaid shirts, and 2 striped shirts. He also has 2 blue ties, 3 red ties, and 3 pink ties. What is the probability that on the first day of school he picks a red tie OR a blue tie
Answers
P(Picking a striped shirt and a pink tie)
= 2/(4 + 3 + 2) * 3/(2 + 3 + 3)
= 2/9 * 3/8
= 1/12
1/12 is the probability that on the first day of school he picks a red tie OR a blue tie.
Probability = number of paths to success. A total number of possible outcomes. For example, the probability of flipping a coin and getting heads is ½. This is because there is one way to get heads and the total number of possible outcomes is 2 (heads or tails). We write P(heads) = ½.
Probability provides information about the probability that something will happen. For example, meteorologists use weather patterns to predict the likelihood of rain. Epidemiology uses probability theory to understand the relationship between exposure and risk of health effects.
Learn more about probability here
https://brainly.com/question/24756209
#SPJ4
help with number 14 please :))

Answers
Answer:
b = - 5
Step-by-step explanation:
(k + a )(k + x) + 1 = k^2 + kx + ak + ax + 1
I think the way to solve this is to worry about the 36
k^s + 1 + ak should equal 36
We know that a = 2
k^2 + 1 + 2k = 36
k^2 + 2k + 1 - 36 = 0
k^2 + 2k - 35 = 0
(k + 7)(k - 5) = 0
k = -7 is the only acceptable answer. It is given that K < 0.
bx = kx + ax
b = k + a
b = - 7 + 2
b = - 5
A triangle has a perimeter of 165 cm. The first side is 65 cm less than twice the second side. The third side is 10 cm less than the second side. Find the length of each side of the triangle.
What equation represents the perimeter of the triangle if the second side is length s?
3s = 165
(2s - 65) + (s) + (s - 10) = 165
(2s + 65) + (s) + (s + 10) = 165
(2s - 65) + (s - 10) = 165
Answers
Answer:
(2s - 65) + (s) + ( s - 10) = 165
Step-by-step explanation:
its the perimeter as per the given question
Answer:
(2s + 65) + (s) + (s + 10) = 165
Step-by-step explanation:
I just took the quiz
what is the answer to |2x-12|=-4x ?
Answers
Answer: -6x
Step-by-step explanation: 24=-4x
24/-4 = -6x
Answer: -6
Step-by-step explanation:
|2x-12|=-4x
if 2x-12 ≥0 or x ≥ 6 then|2x-12|=2x-12
2x-12=-4x
6x=12
x=2 to exclude since x ≥6
if 2x-12 <0 then|2x-12|=-(2x-12)
-2x+12 =-4x
2x =-12
x=-6
Answer x=-6
