NEED HELP
Solve for u. u/6= 3/9 Simplify your answer as much as possible.
Answers
Answer:
u=2
Step-by-step explanation:
u/6= 3/9
simplify the right side
u/6= 1/3
now multiply by 6 on both sides
6x u/6 = 1/3 x6
u= 6/3
simplify;
u=2
Related Questions
The question is above in the photo I could really use the help
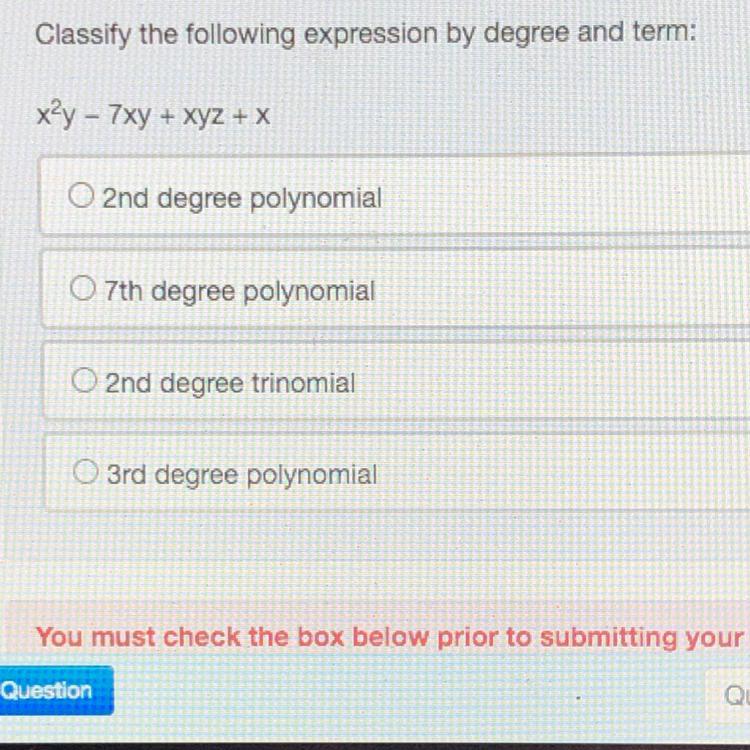
Answers
Answer:
2nd degree trinomial
Because they have three terms ( x ,y and Z ) and highest degree is 2.
Oliver's Flavored Popcorn comes in cylindrical tins divided into three equal sections of caramel, cheese, and buttered flavors. If the tin is 10 inches in diameter and 15 inches tall, what is the volume to the nearest tenth of only the cheese popcorn?
Answers
Answer:
The volume of only the cheese popcorn is 392.5 cubic inches.
Step-by-step explanation:
To determine the volume of only the cheese popcorn,
First, we will determine the volume of the cylindrical tin
The volume of a cylinder is given by
V = πr²h
Where V is the volume of the cylinder
π is a constant, (Take π = 3.14)
r is the radius of the cylinder
and h is the height of the cylinder
From the question, the tin is 10 inches in diameter and 15 inches tall.
Diameter = 10 inches, therefore, we can find radius
Radius = Diameter/2 = 10/2 = 5 inches
r = 5 inches
h = 15 inches
Now, putting the values into the equation, we get
V = 3.14 × 5² × 15
V = 1177.5 cubic inches
This is the volume of the cylindrical tin.
Since the cylindrical tin is divided into three equal sections of caramel, cheese, and buttered flavors, then the volume of only the cheese popcorn will be one-third of the total volume of the cylindrical tin.
∴ The volume of only the cheese popcorn = 1/3 × 1177.5 = 392.5 cubic inches
Hence, the volume of only the cheese popcorn is 392.5 cubic inches.
what would happen if 300 people were sampled instead of 200, and the confidence level remained the same?
Answers
If 300 people were sampled instead of 200, and the confidence level remained the same, it would produce a more accurate result.
Sampling means selecting the group that you will actually collect data from in your research. For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students. In statistics, sampling allows you to test a hypothesis about the characteristics of a population.
This is because a larger sample size allows for a better representation of the population, providing a more accurate result. Additionally, with a larger sample size, the confidence interval of the sample would be narrower, indicating a higher level of confidence in the accuracy of the result.
To learn more about sampling refer :
https://brainly.com/question/6979326
#SPJ11
Suppose that a, b, x and y are real numbers such that ax+by = 1, ax² + by² = 11, ax³ + by³ = 25 and ax⁴ + by⁴ = 83. Find the value of ax⁵ + by⁵.
Answers
Answer:
\(ax^5+ by^5=241\)
Step-by-step explanation:
Given:
\(ax + by = 1\)\(ax^2+ by^2 = 11\)\(ax^3+ by^3 = 25\)\(ax^4+ by^4 = 83\)We can re-write the left sides of the given equations as follows:
\(ax^2+ by^2=(ax+by)(x+y)-xy(a+b)\)
\(ax^3+ by^3=(ax^2+by^2)(x+y)-xy(ax+by)\)
\(ax^4+ by^4=(ax^3+by^3)(x+y)-xy(ax^2+by^2)\)
Therefore, following this pattern:
\(ax^5+ by^5=(ax^4+by^4)(x+y)-xy(ax^3+by^3)\)
Use the given values and the expanded expressions to create 2 equations to help find the values of (x+y) and xy:
Equation 1
\(ax^3+ by^3=(ax^2+by^2)(x+y)-xy(ax+by)\)
\(\implies 25=11(x+y)-xy(1)\)
\(\implies 25=11(x+y)-xy\)
Equation 2
\(ax^4+ by^4=(ax^3+by^3)(x+y)-xy(ax^2+by^2)\)
\(\implies 83=25(x+y)-xy(11)\)
\(\implies 83=25(x+y)-11xy\)
Multiply Equation 1 by 11:
\(\implies 275=121(x+y)-11xy\)
Then subtract Equation 2 from this to eliminate 11xy and find the value of (x+y):
\(\implies 192=96(x+y)\)
\(\implies (x+y)=2\)
Multiply Equation 1 by 25:
\(\implies 625=275(x+y)-25xy\)
Multiply Equation 2 by 11:
\(\implies 913=275(x+y)-121xy\)
Subtract the 2nd from the 1st to eliminate 275(x+y) and find the value of xy:
\(\implies 288=-96xy\)
\(\implies xy=-3\)
Therefore, we now have:
\(ax^4+ by^4 = 83\)\(ax^3+ by^3 = 25\)\((x+y)=2\)\(xy=-3\)Substitute these into the equation for ax⁵ + by⁵ and solve:
\(\implies ax^5+ by^5=(ax^4+by^4)(x+y)-xy(ax^3+by^3)\)
\(\implies ax^5+ by^5=(83)(2)-(-3)(25)\)
\(\implies ax^5+ by^5=166+75\)
\(\implies ax^5+ by^5=241\)
Triangle A B C has centroid G. Lines are drawn from each point through the centroid to the midpoint of the opposite side to form line segments A F, B D, and C E. The length of line segment A G is 19 x + 14 and the length of line segment D G is 9 x + 2.
G is the centroid of triangle ABC.
What is the length of GF?
units
Answers
A triangle is a three-edged polygon with three vertices. It is a fundamental form in geometry. The length of GF is 254 units.
What is a triangle?A triangle is a three-edged polygon with three vertices. It is a fundamental form in geometry. The sum of all the angles of a triangle is always equal to 180°.
Since a centroid of a triangle divides the median into a ratio of 2:1. Therefore, the ratio of AG: DG is,
AG / DG = 2/1
(19x+14)/(9x+20) = 2/1
19x + 14 = 18x + 40
19x - 18x = 40 - 14
x = 26
Assuming the triangle is an equilateral triangle, therefore, the length of GF will be,
GF = DG = 9x+20
GF = DG = 9(26) + 20
GF = 254 units
Hence, the length of GF is 254 units.
Learn more about Triangle:
https://brainly.com/question/2773823
#SPJ1
Answer: 26 units
Step-by-step explanation: Trust Me!!!
The answer is correct on Edge. I just got it right!

a hemispheric bowl with radius 25 contains water whose depth is 10. what is the area of the water's surface?
Answers
The area of the water's surface is approximately 981.25 square units.
Since the water depth is 10, the water fills up half of the hemispheric bowl. Therefore, we need to find the surface area of a circle with radius 25 (the base of the hemisphere) and divide it by 2.
The surface area of a circle with radius r is given by A = πr^2. So, the surface area of the circle with radius 25 is:
A = π(25)^2 = 625π
Dividing by 2, we get
625π/2
So the surface area of the water's surface is 625π/2 square units.
Approximating the value of π as 3.14, we get:
625π/2 ≈ 625(3.14)/2 ≈ 981.25
For such more questions on area
https://brainly.com/question/25292087
#SPJ8
hi
me again
just struggling a bit
what's the reciprocal of 3.5?
would really appreciate your answers
Answers
The expansion of (1 + px +qx2)8 is 1 + 8x + 52x² + kx³+... . Calculate the values of p, q and k.
Ans:
[p = 1, q=3, k = 224]
how do i do this question? It’s binomial theorem.
Answers
Answer:
i think you have to multiply
Step-by-step explanation:
Evaluate: 5^-2=?
HELP
Answers
5^(-2) = (1/5)^(2) = 1/25
Given m || n, find the value of x and y

Answers
Answer:
x = 16 and y = 121
Yes, its a long process.
Step-by-step explanation:
vertical angles are congruent given that: we do this
(4x-5)+(4x-5)+y+y=360
or
2(4x-5)+2y=360
divide both sides by 2
(4x-5)+y=180
distribute (there is an invisible 1 beside the parentheses of 4x-5)
4x-5+y=180
add 5 to both sides
4x+y = 185
subtract y from both sides
4x = 185-y
divide both sides by 4
x = (185-y)/4
note that (4x-5) is also EQUAL to (3x+11)
4x-5=3x+11
subtract 3x from both sides
x-5=11
add 5 to both sides
x = 16
Now that we know what x is, we can substitute it in the equation we got from 2(4x-5)+2y=360
Our equation was
x = (185-y)/4
16 = (185-y)/4
Multiply both sides by 4
64 = 185-y
Subtract 185 from both sides
-121=-y
multiply both sides by -1
121 = y
\The number line shows the balance of Ama's credit card in dollars. For a credit card, a positive balance represents the amount charged to the card.

Answers
The correct matching is given below.
600 ⇒ Amount charged to Ama's credit card
0 ⇒ Zero balance.
|600| ⇒ Difference between Ama's balance and zero balance.
The credit card balance for Ama is displayed on the number line in US dollars. A credit card's positive balance indicates how much has been charged to the card.
A number line is often shown horizontally and can be postponed in any direction.
The number 600 represents the amount charged to Ama's credit card
The number 0 represents the zero balance.
The number |600| represents the difference between Ama's balance and zero balance.
More about the number line link is given below.
https://brainly.com/question/13189025
#SPJ1
Complex numbers are used in electronics to describe the current in an electric circuit. Ohm's law relates the current in a circuit, I, in amperes, the voltage of the circuit, E, in volts, and the resistance of the circuit, R, in ohms, by the formula Solve the problem using this formula. Find E, the voltage of a circuit, if I = (16 + i) amperes and R = (2 + 4i) ohms.
Answers
Answer:
E = (28 + 66i) Volts
Step-by-step explanation:
Note that: i = √-1 ; i² = -1
Ohm's law: E = IR
E = (16+ i) (2 + 4i)
Expand the equation.
E = 16x2 + 16x4i + ix2 + ix4i
E = 32 + 64i + 2i + 4i²
E = 32 + 64i + 2i + 4(-1)
E = 32 + 64i + 2i - 4
Collect like terms:
E = 32 -4 + 64i + 2i
E = (28 + 66i) Volts
(3x³x+4) /(x − 2)
Help
Answers
Answer:
3x^4 + 4 / x - 2
Step-by-step explanation:
(3x³x+4) /(x − 2)
3(x ⋅ x^3) + 4 / x - 2
3x^4 + 4 / x - 2
We can't simplify anymore, so the answer is 3x^4 + 4 / x - 2
ASAP!!! and no links please 25 points!!!!!
The radius of a can of soda is 0.75 inches. Find the area of the top of the can. Round to the nearest hundredth.
(Values only! No units!)
Answers
Answer:
2.36
Step-by-step explanation:
Multiply the radius (0.75) with the value of pi (3.14.....)
0.75 x pi = area
area = 2.35619449019
ROUNDED TO HUNDREDTHS = 2.36
hope this helps :)
how many ways are there to distribute six objects to five boxes if a) both the objects and boxes are labeled? b) the objects are labeled, but the boxes are unlabeled? c) the objects are unlabeled, but the boxes are labeled? d) both the objects and the boxes are unlabeled?
Answers
a) For labeled objects and boxes, there are 5⁶ = 15,625 possible distributions. b) For labeled objects and unlabeled boxes, there are 792 possible distributions. c) For unlabeled objects and labeled boxes, there are 5C6 = 5 possible distributions.d) There is only 1 possible distribution.
a) When both the objects and boxes are labeled, each object can be placed in any of the five labeled boxes, giving us 5 choices for each object. Since there are six objects in total, the total number of distributions is 5⁶ = 15,625.
b) When the objects are labeled but the boxes are unlabeled, we can use a technique called stars and bars. We have 6 objects (stars) and 5 boxes (bars). The objects can be distributed by placing the bars between the objects, so there are (6 + 5 - 1) choose (5 - 1) = 792 possible distributions.
c) When the objects are unlabeled but the boxes are labeled, we have 5 boxes, and we need to choose 6 objects to fill them. This can be thought of as choosing a subset of 6 objects out of 5, which can be done in 5C6 = 5 ways.
d) When both the objects and the boxes are unlabeled, there is only one possible distribution. Since the objects and boxes are indistinguishable, it does not matter which object goes into which box, resulting in a single distribution.
Learn more about distributions here: https://brainly.com/question/30653447
#SPJ11
Line AB and line BC form a right angle at point B. If A = (2, 5) and B = (4, 4), what is the equation of line BC?
Answers
Answer:
y = 2x - 4
Step-by-step explanation:
To solve this problem, we must first calculate the slope of the line AB using the formula:
\(\boxed{m = \frac{y_2 - y_1}{x_2 - x_1}}\)
where:
m ⇒ slope of the line
(x₁, y₁), (x₂, y₂) ⇒ coordinates of two points on the line
Therefore, for line AB with points A = (2, 5) and B = (4, 4) :
\(m_{AB} = \frac{5 - 4}{2 - 4}\)
⇒ \(m_{AB} = \frac{1}{-2}\)
⇒ \(m_{AB} = -\frac{1}{2}\)
Next, we have to calculate the slope of the line BC.
We know that the product of the slopes of two perpendicular lines is -1.
Therefore:
\(m_{BC} \times m_{AB} = -1\) [Since BC and AB are at right angles to each other]
⇒ \(m_{BC} \times -\frac{1}{2} = -1\)
⇒ \(m_{BC} = -1 \div -\frac{1}{2}\) [Dividing both sides of the equation by -1/2]
⇒ \(m_{BC} = \bf 2\)
Next, we have to use the following formula to find the equation of line BC:
\(\boxed{y - y_1 = m(x - x_1)}\)
where (x₁, y₁) are the coordinates of a point on the line.
Point B = (4, 4) is on line BC, and its slope is 2. Therefore:
\(y - 4 =2 (x - 4)\)
⇒ \(y - 4 = 2x - 8\) [Distributing 2 into the brackets]
⇒ \(y = 2x-4\)
Therefore, the equation of line BC is y = 2x - 4.
Hannah walked 3/4 of the way from school to home. a.What fractional part of the distance from school to her home does she have left to walk? b.The remaining distance is what fractional she has already walked?
Answers
Answer:
1/4 left not sure what you are asking for b
Step-by-step explanation:
The whoe way home would be 4/4. So you subtract 3/4 from 4/4 and that tells you what she has left to walk.
A marble statue has a mass of 1600 kg and is
270 cm tall.
The density of marble is 2500 kg/m³.
Justin makes a mathematically similar model
of the statue out of clay.
The model is 45 cm tall and has a density of
1200 kg/m³.
What is the mass of Justin's model?
Give your answer to 3 significant figures

Answers
Answer:
3.56 kg
Step-by-step explanation:
You want the mass of a model that is 45 cm tall and has a density of 1200 kg/m³ when the statue it is modeling is 270 cm tall, has a density of 2500 kg/m³, and a mass of 1600 kg.
VolumeThe ratio of volumes of the model to the statue is the cube of the ratio of their heights:
Vm/Vs = (Hm/Hs)³
Vm = Vs(Hm/Hs)³ = (1600 kg)/(2500 kg/m³)·((45 cm)/(270 cm))³
Vm ≈ 0.002963 m³
MassThe mass of the model is the product of its volume and its density:
Mm = Vm·ρ = (0.002963 m³)(1200 kg/m³) ≈ 3.56 kg
The mass of Justin's model is about 3.56 kg.
__
Additional comment
The relationship between density, volume, and mass is ...
ρ = mass/volume
This can be rearranged to ...
volume = mass/ρ
Which is the expression we used for Vs in the first section above.
(We used V and H for volume and height with 'm' and 's' signifying the model and the statue, respectively.)
<95141404393>

The mass of Justin's model is approximately 3.57 kg., rounded to 3 significant figures.
How to find the mass of Justin's modelTo find the mass of Justin's model, we can use the concept of mathematical similarity.
Mathematical similarity means that corresponding dimensions of two objects are proportional. In this case, Since the densities are also given, we can use the volume ratio to find the mass ratio.
Let's calculate the volume ratio first:
Volume ratio = (Height of model / Height of statue)^3
= (45 cm / 270 cm)^3
= (0.1667)^3
= 0.00463
Now, using the density ratio:
Density ratio = Density of model / Density of statue
= 1200 kg/m³ / 2500 kg/m³
= 0.48
Finally, we can find the mass of Justin's model by multiplying the mass of the statue by the volume ratio and density ratio:
Mass of Justin's model = Mass of statue * Volume ratio * Density ratio
= 1600 kg * 0.00463 * 0.48
= 3.5712 kg
Rounding to 3 significant figures, the mass of Justin's model is approximately 3.57 kg.
Learn more about mass at https://brainly.com/question/86444
#SPJ1
What is the median?
A(18
B(27
C(33.2
D(34.5

Answers
Answer: 34.5
Step-by-step explanation:
First, write out all of the numbers from least to greatest.
which is (18,20,26,34,34,35,38,40,42,45)
Second, choose the number in the middle of the set of numbers you wrote out from least to greatest. (There are TWO numbers in this case, which are 34 and 35)
Lastly, since there are two numbers you add them both together and then divide by 2. (34+35=69 , 69 divided by 2 = 34.5)
. A doughnut mix requires 3 cups of sugar for every 15 doughnuts. How much sugar is used per doughnut?
Answers
Answer:
45
Step-by-step explanation:
15x3=45
ok i help and answers

Answers
Combining the like terms, the equivalent expressions are given as follows:
-15a - 3b + 16a + 4b = a + b.2a - 4b - 3a + 6b + 6 = -a + 2b + 6.2a + 2b - 6a -3 - 2b + 6 = -4a + 3.3a - 6b - 6 + 2a + 6b + 2 = 5a - 4.3a + 4a + 2b - 4 - 5b - 10 = 7a + 7b - 14.How do we add and subtract symbolic expressions?To add or subtracted symbolic expressions, in which the terms are accompanied by letters, we combine the like terms, that is, we add or subtract terms that have the same letter.
One example is:
a + b + 3a + 20b = 4a + 21.
As 1 + 3 = 4, 1 + 20 = 21.
Hence the equivalent expressions for the first space is:
-15a - 3b + 16a + 4b = a + b.
For the second space, it is:
2a - 4b - 3a + 6b + 6 = -a + 2b + 6.
For the third space, it is:
2a + 2b - 6a -3 - 2b + 6 = -4a + 3.
For the fourth space, it is:
3a - 6b - 6 + 2a + 6b + 2 = 5a - 4.
For the fifth space, it is:
3a + 4a + 2b - 4 - 5b - 10 = 7a + 7b - 14.
More can be learned about addition and subtraction of expressions at https://brainly.com/question/723406
#SPJ1
Is 3 to the second power + 3 to the 3rd power equal to 3 to the 5th power explain

Answers
Answer:
They are not equal.
Step-by-step explanation:
Hi there!
\(3^2+3^3\) is not equal to \(3^5\). When two powers with the same base are added together, we cannot add the exponents to get the answer.
We can only add exponents to get the answer when two power with the same base are multiplied.
\(3^2+3^3\\= 9+27\\=36\)
\(3^5\\=243\)
They are not equal.
I hope this helps!
The third, fifth and eighth terms of an AP are the first 3 consecutive terms of a GP. Given that the first term of the AP is 8, calculate the common difference
Answers
Answer:
The common difference = 2.
Step-by-step explanation:
An AP can be written as a1, a1 + d, a1 + 2d, a1 + 3d, a1 + 4d, a1 + 5d, a1 + 6d , a1 + 7d.
where a1 = first term and d is the common difference.
Here first term = a1 = 8
3rd term = a1 + 2d = 8 + 2d
5th term = a1 + 4d = 8 + 4d
8th term = 8 + 7d
First 3 terms of a GP are a , ar and ar^2
So from the given information:
a = 8 + 2d
ar = 8 + 4d
ar^2= 8 + 7d
Dividing the second equation by the first we have
r = (8 + 4d)/(8 + 2d)
Dividing the third by the second:
r = (8 + 7d) / (8 + 4d)
Therefore, eliminating r we have:
(8 + 4d)/(8 + 2d) = (8 + 7d)/(8 + 4d)
(8 + 4d)^2 = (8 + 2d)(8 + 7d)
64 + 64d + 16d^2 = 64 + 72d^ + 14d^2
2d^2 - 8d = 0
2d(d^2 - 4) = 0
2d = 0 or d^2 = 4, so
d = 0, 2.
The common difference can't be zero so it must be 2.
one year, the population of a city was 359,000. several years later it was 420,030. find the percent increase.
Answers
Answer:
17%
Step-by-step explanation:
The yield of corn in bushels per acre and the amount of rain in the growing season.
Identify the explanatory variable and the response variable, if possible.
1. Amount of rain is the explanatory variable and yield of corn is the response variable.
2. Bushels per acre is the explanatory variable and amount of rain is the response variable.
3. Yield of corn is the explanatory variable and amount of rain is the response variable.
4. Amount of rain is the explanatory variable and bushels per acre is the response variable.
5. Rain is the explanatory variable and corn is the response variable.
Answers
Answer:
1. Amount of rain is the explanatory variable and yield of corn is the response variable.
Step-by-step explanation:
Explanatory Variable is the causal variable, which effects the other variable.
Response Variable is the resultant variable, which is effected by the other variable.
In this case, amount of rain effects the yield of corn (bushels per acre).
So, Amount of rain being causal effecting variable - is Explanatory Variable. Corn yield, being resultantly effected variable - is Response Variable.
In Exercises 1 and 2, find m/1 and m<2
1.

Answers
Answer:
m/1 = 87
m/2 = 93
Step-by-step explanation:
m1 and m2 need to have an angle of 180
so 180-87 = 93
In ∆OPQ, q =18cm, o=96cm and
Answers
Given the information on the problem, we can use the law of cosines to find the length of p with the following equation:
\(p^2=q^2+o^2-2q\cdot o\cdot\cos P\)substituting the values at hand, we get the following:
\(\begin{gathered} p^2=(18)^2+(96)^2-2(18)(96)\cos 142 \\ \Rightarrow p^2=324+9216+2723.37 \\ \Rightarrow p^2=12263.37 \\ \Rightarrow p=\sqrt[]{12263.37}=110.74 \\ p=110.7\operatorname{cm} \end{gathered}\)therefore, the length of p is 111 cm
PLS HELP!!!
I attached the question in the picture below

Answers
a+6=7 and a+6=-7
For a+6=7
Subtract 6 from both sides
a=1
For a+6=-7
Again subtract 6 from both sides
a=-13
Therefore, the last answer is correct
A math textbook has a length of 22 cm, a width of 27 cm, and a height of 3.5
cm. A science textbook has a length of 21 cm, a width of 27 cm, and a height
of 4 cm.
Which textbook has a greater volume?
OA. The science textbook, with a volume of 2376 cm³
OB. The math textbook, with a volume of 2464 cm³
OC. The math textbook, with a volume of 2079 cm³
OD. The science textbook, with a volume of 2268 cm³
Answers
The science textbook has a greater volume than the math textbook, so option D is correct, the science textbook, with a volume of 2268 cm³.
The volume of a rectangular prism is given by the formula V = lwh, where l is the length, w is the width, and h is the height.
Using this formula, we can calculate the volumes of the math and science textbooks:
Math textbook:
V = 22 cm × 27 cm × 3.5 cm
= 2079 cm³
Science textbook:
V = 21 cm × 27 cm × 4 cm
= 2268 cm³
Therefore, the science textbook has a greater volume than the math textbook, so option D is correct, the science textbook, with a volume of 2268 cm³.
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
please help me I’m struggling

Answers
Answer:
c
Step-by-step explanation:
the answer is c becuase i know this que
Answer:
All
Step-by-step explanation:
We can check it by using the Pythagorean theorem.
\(a {}^{2} + b {}^{2} = c {}^{2} = {3}^{2} + { \sqrt{27} }^{2} = 6 {}^{2} = 9 + 27 = 36 = 36 = 36 \)
\( {a}^{2} + {b}^{2} = c {}^{2} = {8}^{2} + {15}^{2} = {17}^{2} = 64 + 225 = 289 = 289 = 289\)
\(a {}^{2} + b {}^{2} = c {}^{2} = 5 {}^{2} + {5}^{2} = { \sqrt{50} }^{2} = 25 + 25 = 50 = 50 = 50 = \)
Hope this helps ;) ❤❤❤