Next → The Unit Circle: Mastery Test
The measure of angle 0 is 7pi/4. The measure of its reference angle is and tan 0 is
Answers
Therefore, the reference angle of 7π/4 is 3π/4, and tan 0 = 1.
What is trigonometry?Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles, especially right triangles. It involves the study of trigonometric functions such as sine, cosine, tangent, and their inverses, as well as their applications in various fields such as physics, engineering, and navigation. Trigonometry is an important tool for solving problems involving angles, distances, and heights, among others.
Here,
The reference angle for an angle θ is the positive acute angle formed by the terminal side of θ and the x-axis.
To find the reference angle for 7π/4, we can subtract π from it since the angle is in the fourth quadrant.
Reference angle = 7π/4 - π
= 3π/4
To find tan 0, we need to use the tangent function:
tan θ = opposite/adjacent
Since we don't know the sides of the triangle, we need to use the reference angle to find the ratio.
The reference angle of 3π/4 is in the second quadrant, where x is negative and y is positive. We can draw a triangle with sides of length 1, 1, and √2, where the hypotenuse is the line with angle 3π/4.
Then, tan(3π/4) = opposite/adjacent
= 1/-1
= -1
So, tan 0 = tan (7π/4)
= tan (3π/4 + π)
= -tan(3π/4)
= -(-1)
= 1.
To know more about trigonometry,
https://brainly.com/question/29002217
#SPJ1
Related Questions
The percentage of total variation in the dependent variable that is described by the independent variable is expressed by_________.
a. coefficient of determination
b. correlation coefficient
c. coefficient of covariation
d. regression coefficient
a. coefficient of determination
Answers
The percentage of total variation in the dependent variable that is described by the independent variable is expressed by coefficient of determination . So, correct answer is option (a).
The coefficient of determination R² is equal to the square of the correlation coefficient, r² expressed as a percentage, represents the percentage of variation in the dependent variable y that can be explained by variation in the independent variable x using the regression line. Coefficient of determination is a statistical measure that examines how differences in one variable can be explained by differences in her second variable. In other words, this coefficient, commonly known as R-squared (or R²), measures how strong the linear relationship between two variables is. This coefficient is commonly known as the R-square (or R²) and is sometimes called the "goodness of fit". This measurement is expressed as a value between 0.0 and 1.0..
To learn more about Cofficient of determination, refer:
https://brainly.com/question/17237825
#SPJ4
A regular hexagon is rotated about its center. Which degree measure will carry the regular hexagon onto itself?
A. 45
B. 90
C. 120
D. 135
Answers
Answer:
120 Degrees
Step-by-step explanation:
(6-2)*180 = 720
720/6 = 120
So the answer is 120
Hope this helps!
The degree will carry the regular hexagon onto itself is 60 degrees.
What is a regular hexagon?"A regular hexagon is a closed shape polygon which has six equal sides and six equal angles. In case of any regular polygon, all its sides and angles are equal. When we arrange six equilateral triangles side by side, then a regular hexagon is composed. Then, the area of the regular hexagon becomes equal to six times the area of the same triangle."
Regular Hexagon Properties
1. It has 6 equal sides and 6 equal angles.
2. It has 6 vertices.
3. Sum of interior angles equals 720°.
4. Interior angle is 120° and exterior angle is 60°.
5. It is made up of six equilateral triangles.
6. 9 diagonals can be drawn inside a regular hexagon.
7. All the sides opposite to each other are parallel.
We know
There are 6 sides to a hexagon
360 degrees in a hexagon
The degree will carry the regular hexagon onto itself
= \(\frac{360}{6}\)
= \(60^{0}\)
Thus, The degree will carry the regular hexagon onto itself is 60 degrees.
Learn more about regular hexagon here
https://brainly.com/question/1694257
#SPJ2
Write the slope-intercept form of the equation of the line.
slope = 1, y, int = -2

Answers
Answer:
y = x - 2
General Formulas and Concepts:
Algebra I
Slope-Intercept Form: y = mx + b
m - slope b - y-interceptStep-by-step explanation:
Step 1: Define
Slope m = 1
y-intercept b = -2
Step 2: Write linear function
y = x - 2
Answer: B, y=x-2
Step-by-step explanation:
The slope-intercept form is y=mx+b where m=slope and b=y intercept
therfore, subtituting 1 for m and -2 for b
y=x-2
Complete the proof of the identity by choosing the rule that justifies each step.(1-cosx)(1+cosx)=sin^2x

Answers
You have the following expression:
\((1+cosx)(1-\cos x)=\sin ^2x\)To verify the identity, you have that the left side of the equation becomes:
(1 + cosx)(1 - cosx) = (1 - cos^2 x)
because of the product of an expression by its conjugate result in a difference of squares. Or simplfy by expanding the factors and simplying.
Next, you have:
1 - cos^2 x = sin^2 x
because the Pythagorean identity.
Then, the identity is verified.
The first term of an arithmetic sequence is 10 and its
common difference is -3. What is the sum of the first
10 terms of this sequence?
Please hurry! ill give brainliest
Answers
Answer:
The sum of the first ten terms is -35.
Step-by-step explanation:
The first term of an arithmetic sequence is 10, and its common difference is -3.
We want to find the sum of the first 10 terms of this sequence.
Remember that the sum for an arithmetic sequence is given by:
\(\displaystyle S=\frac{k}{2}\left(a+x_k\right)\)
Where k is the number of terms, a is the initial/first term, and x_k is the last term.
Since our initial term is 10, a = 10.
And since we want to find the sum of the first ten terms, k = 10.
So, we will need to find the last or tenth term. We can write an explicit formula. The standard explicit formula for an arithmetic sequence is:
\(x_n=a+d(n-1)\)
Where a is the initial term and d is the common difference.
So, by substituting, we acquire:
\(x_n=10-3(n-1)\)
Then the tenth or last term is:
\(x_{10}=10-3(10-1)=10-3(9)=10-27= -17\)
Then the sum of the first ten terms will be:
\(\displaystyle S_{10}=\frac{10}{2}(10+(-17))=5(-7)=-35\)
Answer:
-35
Step-by-step explanation:
\(a_{1}\) = 10+(-3)(0) = 10
\(a_{10}\) = 10+(-3)(9) = -17
\(S_{10}\) = 10[(10 -17)/2] = 10(-7/2) = -70/2
Given the vectors u= <2, 1> and v= <5, 4>, determine the components of a vector represented by 2u - 3v
A.) <14, 15>
B.) <-6, -9>
C.) <-11, -10>
D.) <19, 14>
Answers
Answer:
C.) <-11, -10>
Step-by-step explanation:
Let's define how to work with vectors.
For two vectors:
V = <a, b>
W = <c, d>
The product of a scalar k and a vector is given by:
k*V = k*<a, b> = <k*a, k*b>
And the sum (or difference) of two vectors is given by:
V ± W = <a, b> ± <c, d> = <a ± c, b ± d>
Now that we know this, we can solve the problem.
Here we have the vectors:
u = <2, 1>
v = <5, 4>
then:
2u - 3*v = 2*<2, 1> - 3*<5, 4>
= <2*2, 2*1> - <3*5, 3*4>
= <4, 2> - <15, 12>
= <4 - 15, 2 - 12>
= < -11, -10>
Then the correct option is C.
Can sum1 hurry and give me the answers to theses pls !!

Answers
Answer:
i dont understand what you want us to do lol?
Step-by-step explanation:
Answer:
Step-by-step explanation:
do u have an actual pictrue of problem 8 & 10 ?
I'm just going to drop this here!

Answers
The 3rd graph (bottom left)
2.58
Devide 30% by 100 and remove the percent sign to convert From a percent to a decimal show me the solution
Answers
Answer:
Step-by-step explanation:
Answer:
0.003
Step-by-step explanation:
(30%)/100
Result
0.003
Decimal approximation
0.003
Rational approximation
3/1000
how many rooms are there in the house?
Answers
Answer:
1 or more than 1
Step-by-step explanation:
This is your answer
Find the area of this composite figure

Answers
Answer:
23.9425 (Round if needed)
Step-by-step explanation:
This is 2 half circles so you can find the area of a circle and divide it by 2.
First circle has a diameter of 6 cm
6/2=3 cm
So, circle has radius of 3.
Area of circle= 3.14(pi) radius^2
3.14 x 3^2= 28.26
28.26/2=14.13 cm
Area of first half circle= 14.13
Repeat that process for the second circle.
3.14 x 2.5^2=19.625
19.625/2=9.8125
14.13+9.8215=23.9425
Area=23.9425
10. in July, Ariel recorded the height of a pine tree and how quickly it was expected to grow in the
next several months.
a. Write an equation for the table.
Number of
Months
Height of
Tree (inches)
0
600
3
602
b. What does the slope represent?
6
604
606
12
608
C. What does the y-intercept represent?
ere to search
O

Answers
In triangle ABC acute angles are in the ratio 5:1, i.e.
Answers
Answer:
The quen is as following:
ABC is a right triangle at C,
Acute angles are in the ratio 5:1, i.e. ∠BAC : ∠ABC = 5:1
If CH is an altitude to AB and CL is an angle bisector of ∠ACB, find m∠HCL.
The solution is: m∠HCL = 30°
Step-by-step explanation:
See the attached figure.
∵The triangle is right at C ∴∠C = 90°
∴∠A + ∠B = 90° ⇒(1)
∵ Acute angles are in the ratio 5:1, i.e. ∠BAC : ∠ABC = 5:1
∴∠A = 5 times ∠B
Substitute at (1)
∴ 5 ∠B + ∠B = 90° ⇒⇒⇒ ∴∠B = 15° and ∠A = 75°
∵CL is an angle bisector of ∠ACB
∴ ∠ACL = 90°/2 = 45°
∵ CH is an altitude to AB ⇒ ∠CHA = 90°
At the triangle AHC:
∠ACH = 180° - (∠CHA + ∠CAH) = 180° - (90° + 75°) = 15°
∴ ∠HCL = ∠ACL - ∠ACH = 45° - 15° = 30°
select all expressions that are true when x=2
x/2+1=0
3x-4=2
x-4< -3
2x+1 > 0
Answers
Answer:
Solution for Find the exact value of the expression cos 11π/6. ... Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!* ... Q: The pair of equations x+2y+5 = 0 and -3x-6y+1=0 have how many ... of the tangent line to the graph of f(æ) = (e¯")² at a = - In 2 is Select one: O a. y + . ... All Rights Reserved.
What is the center of the circle given by the equation
(x - 2)^2 + (y + 4)^2 = 6?
A. (-2,-4)
B. (2,-4)
C. (-2,4)
D. (2,4)
Answers
Answer:
B: (2,-4)
Step-by-step explanation:
x-2=0
x=2
y+4=0
y=-4
**Solve each problem below. Be sure to write an equation, solve the problem, and answer
the question in a complete sentence. (3 points each)
4. Kelsey made a pitcher of lemonade. She drank 1/6 of the pitcher for lunch and 2/3 of the
pitcher for dinner. How much of the pitcher of lemonade did Kelsey drink altogether?
Equation:
Answer:
Sentence:
5. Karen had 4 % yards of fabric. She used 3 1/2 yards for a skirt. How much fabric was left?
Answers
Answer:
hyee
Step-by-step explanation:
hope this helps :)

Which statement about the following equation is true
Answers
Options: A. The equation -3|2x + 1.2| = -1 has no solution
B. The equation 3.5|6x - 2| = 3.5 has one solution
C. The equation 5|-3.1x + 6.9| = -3.5 has two solutions
D. The equation -0.3|3 + 8x| = 0.9 has no solution
The correct answer is D. The equation -0.3|3 + 8x| = 0.9 has no solution
Step-by-step explanation:
I just took the test and got 100%
Activity
You have also set up a card game in which a player picks a card from a standard deck of 52 cards. The player wins if these two events occur together: E1, in which the card drawn is a black card, and E2, in which the card drawn is a numbered card, 2 through 10.
Question 1
What is the probability of getting a black card and a numbered card? Calculate the probabilities P(E1) and P(E2) as fractions.
Answers
The probability of getting a black card and a numbered card is 9/26.
To calculate the probability of getting a black card (E1), we need to determine the number of black cards in a standard deck of 52 cards.
There are 26 black cards in total, which consist of 13 spades (black) and 13 clubs (black).
Therefore, the probability of drawing a black card (P(E1)) is:
P(E1) = Number of favorable outcomes / Total number of possible outcomes
P(E1) = 26 / 52
Simplifying this fraction, we get:
P(E1) = 1/2
So the probability of drawing a black card is 1/2.
To calculate the probability of drawing a numbered card (E2), we need to determine the number of numbered cards (2 through 10) in a standard deck.
Each suit (spades, hearts, diamonds, clubs) contains one card for each numbered value from 2 to 10, totaling 9 numbered cards per suit.
Therefore, the probability of drawing a numbered card (P(E2)) is:
P(E2) = Number of favorable outcomes / Total number of possible outcomes
P(E2) = 36 / 52
Simplifying this fraction, we get:
P(E2) = 9/13
So the probability of drawing a numbered card is 9/13.
To calculate the probability of both events occurring together (getting a black card and a numbered card), we multiply the individual probabilities:
P(E1 ∩ E2) = P(E1) × P(E2)
P(E1 ∩ E2) = (1/2) × (9/13)
Simplifying this fraction, we get:
P(E1 ∩ E2) = 9/26
Therefore, the probability of getting a black card and a numbered card is 9/26.
For such more questions on probability
https://brainly.com/question/25839839
#SPJ8
PLEASE HELP WILL MARK BRAINLIEST!!! No links and serious answers only!!
2. Write the equation of the line of best fit using the slope-intercept formula $y = mx + b$. Show all your work, including the points used to determine the slope and how the equation was determined.
3. What does the slope of the line represent within the context of your graph? What does the y-intercept represent?
4. Test the residuals of two other points to determine how well the line of best fit models the data.
5. Use the line of best fit to help you to describe the data correlation.
6. Using the line of best fit that you found in Part Three, Question 2, approximate how tall is a person whose arm span is 66 inches?
7. According to your line of best fit, what is the arm span of a 74-inch-tall person?

Answers

Below is the graph of a trigonometric function. It has a minimum point at
(1, 1.5) and an amplitude of 1.5. What is the midline equation of the function?
Answers
The midline equation of the function is y = 1.5.
What is amplitude of trigonometric functions?The gap between a trigonometric function's highest and least values is known as its amplitude. The difference between the greatest and minimum numbers is, in other words, divided by two. For instance, the amplitude is A in the equation y = A sin(Bx) + C. The amplitude, also known as the average value of the function across a period, denotes the "height" of the function above and below the midline. It gauges the magnitude or intensity of the oscillation of the function's representation of. The oscillation is more prominent and subtler depending on the amplitude, which ranges from higher to lower values.
Given that, the function has minimum point at (1, 1.5) and an amplitude of 1.5.
Using the definition of the amplitude the midline is the given amplitude.
Hence, the midline equation of the function is y = 1.5.
Learn more about amplitude here:
https://brainly.com/question/9124856
#SPJ1
Answer:
3
Step-by-step explanation:
Khan Academy
Select the correct answer from each drop-down menu.
The graph of g(x) is shown.
y +10
-10
10
-5
-10
The graph of h(x) = g(x + 5) has
v and

Answers
Answer:
If \(g(x) = f(x+5)\), then horizontal asymptote is the same.
Step-by-step explanation:
The graph represented in the figure is a hyperbola of the form:
\(y = \frac{A}{(x-k)} + B\) (1)
Where:
\(x\) - Indendent variable.
\(y\) - Dependent variable.
\(k\) - Horizontal coordinate where vertical asymtote goes through.
\(A, B\) - Coefficients.
When \(x = k\), the equation becomes undefined and vertical asymptote passes through \((x, y) = (k, 0)\). If \(x \to \pm \infty\), then \(y \to B\), coinciding with the horizontal asymptote.
The graph have the following parameters: \(k = 2\), \(B = 3\). If \(g(x) = f(x+5)\), then horizontal asymptote is the same.
Answer:
The graph of h(x) = g(x + 5) has
the same horizontal asymptote as function g
and
a vertical asymptote at x = -7
Step-by-step explanation:

Can you show steps please?

Answers
Given the Initial principal and interest rate, the time taken for the value of the investment to reach $20,000 is 14.1 Years.
What is an interest in banking?An Interest is simply the amount of money a lender or financial institution receives for lending out money or pays for receiving money.
The formular for calculating compound interest is expressed as;
A = P(1 + r/n)^(n*t)
Where A is final amount, P is initial principal balance, r is interest rate, n is number of times interest applied per time period and t is number of time periods elapsed.
Given the data in the question;
Initial principal balance P = $8000Interest rate r = 6.5% annual interested = 0.065Compounded daily n = 365 daysFinal amount A = $20000Time t = ?A = P(1 + r/n)^(n*t)
We make t the subject of the formula
t = In(A/P) / n[In(1 + r/n)]
t = In(20000/8000) / 365[In( 1 + 0.065/365 )]
t = In(2.5) / 365[In( 1 + 1.78×10⁻⁴ )]
t = In(2.5) / 365[In( 1.000178 )]
t = In(2.5) / 365[In( 1.000178 )]
t = 0.91629 / ( 365 × 0.00017798 )
t = 14.1 years
Given the Initial principal and interest rate, the time taken for the value of the investment to reach $20,000 is 14.1 Years.
Learn more about compound interest here: brainly.com/question/27128740
#SPJ1
Which expression is equivalent to 4(2p+4q)
Answers
Answer:
8p+16q
hope this helps
4x2p=8p
4x4q=16q
-3r + 18 = 15r please help!!
Answers
Answer:
r = 1
Step-by-step explanation:
Step 1: Write equation
-3r + 18 = 15r
Step 2: Solve for r
Add 3r to both sides: 18 = 18rDivide both sides by 18: 1 = rRewrite: r = 1Step 3: Check
Plug in r to verify it's a solution.
-3(1) + 18 = 15(1)
-3 + 18 = 15
15 = 15
Step-by-step explanation:
- 3r - 15r = -18 .... Moved variables to one side and constants to the other
- 18r = - 18 ..... Simplified
r = 1 ..... Divided to isolate the r
Check:
Plug in 1 for r
-3(1) +18 = 15(1)
- 3+18 = 15
15 = 15 .... Therefore 1 is correct
Answer is 1
Hope this helps!
Find the value of x. You may assume triangle ABC is similar to triangle STU.
(click on the photo to make it better quality) PLEASE HELP!!!

Answers
By applying the concept of corresponding angles in similar triangles, we were able to establish the value of x as 25 in the given scenario.
In the given problem, we are provided with information about the angles in two similar triangles: triangle ABC and triangle STU. It is stated that angle UTS in triangle STU is 100 degrees, and since corresponding angles of similar triangles are congruent, we can conclude that angle STU is also 100 degrees.
Next, we examine angle BAC in triangle ABC, which is given as 4x. Using the same logic, we know that angle BAC is also congruent to angle STU. Therefore, we can equate the two angles:
angle BAC = angle STU
4x = 100
To find the value of x, we divide both sides of the equation by 4:
x = 100/4
x = 25
Hence, we determine that x is equal to 25. This method allows us to leverage the known information about one triangle to infer the measurements of corresponding angles in the other similar triangle.
For more such questions on triangle
https://brainly.com/question/2773823
#SPJ8
Jasmine has a circular swimming pool with a radius of 4.2 meters. What is the circumference of the pool? Use 3.14 for π
. Round to the nearest hundredth if necessary.
__ m
Answers
If the radius of Jasmine's swimming pool is 4.2 meter, then it's circumference is 26.4 meters.
The "Circumference" of a circle is known as the distance around the boundary of a circle.
The circumference of a circle is given by the formula : 2 × π × radius,
where π (pi) is a mathematical constant approximately equal to 3.14,
We are given that Jasmine's swimming pool has a radius of 4.2 meters.
So, we can calculate the circumference of the pool as :
⇒ Circumference = 2 × 3.14 × 4.2 meters,
⇒ Circumference ≈ 26.4 meters,
Therefore, the circumference of Jasmine's swimming pool is 26.4 meters.
Learn more about Circumference here
https://brainly.com/question/16125353
#SPJ1
Please help me out!!!

Answers
Answer:
Shifts 4 units down ---> \(g(x)=2x-10\)
Stretches f(x) by a factor of 4 away from x-axis--->\(g(x)=8x-6\)
Shifts f(x) 4 units right---> \(g(x)=2x-14\)
Compress f(x) by a factor of 1/4 toward the y-axis ---> \(g(x)=1/2x-3/2\)
Step-by-step explanation:
We are given \(f(x)=2x-6\)
We need to match the transformations.
1) shifts f(x) 4 units down.
When function f(x) shifts k units down the new function becomes f(x)-k
In our case
\(g(x)=2x-6-4\\g(x)=2x-10\)
So, Shifts 4 units down ---> \(g(x)=2x-10\)
2) Stretches f(x) by a factor of 4 away from x-axis
When function f(x) is stretched by a factor of b away from x-axis the new function becomes f(bx)
\(g(x)=2(4x)-6\\g(x)=8x-6\)
So, Stretches f(x) by a factor of 4 away from x-axis--->\(g(x)=8x-6\)
3) Shifts f(x) 4 units right
When function f(x) shifts h units right the new function becomes f(x-h)
\(g(x)=2(x-4)-6\\g(x)=2x-8-6\\g(x)=2x-14\)
So, Shifts f(x) 4 units right---> \(g(x)=2x-14\)
4) Compress f(x) by a factor of 1/4 toward the y-axis
When function f(x) is compressed by h factor of a toward the y-axis the new function becomes h.f(x)
\(g(x)=1/4(2x-6)\\g(x)=1/2x-3/2\)
Compress f(x) by a factor of 1/4 toward the y-axis ---> \(g(x)=1/2x-3/2\)
(Option Not given)
(If we compress f(x) by a factor of 4 towards y-axis we get g(x)=8x-24)
-10.3r = 1.03 what is R?

Answers
Answer:
r= -0.1
Step-by-step explanation:

HELP PLEASE!!
Quadrilateral CDEF is a rhombus. What is m

Answers
Answer:
∠ BDC = 29°
Step-by-step explanation:
the sides of a rhombus are congruent, so CD = ED and Δ EDC is therefore isosceles with base angles congruent , then
∠ BCD = ∠ BED = 61°
• the diagonals are perpendicular bisectors of each other , then
∠ CBD = 90°
the sum of the 3 angles in Δ BCD = 180°
∠ BDC + ∠ CBD + ∠ BCD = 180°
∠ BDC + 90° + 61° = 180°
∠ BDC + 151° = 180° ( subtract 151° from both sides )
∠ BDC = 29°
Find the distance between the points P and Q shown.
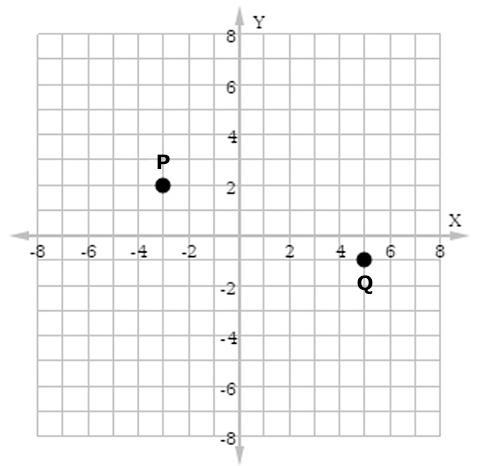

Answers
The distance between points P and Q is √73
How to find the distance between the two points?First, remember that the distance between two points whose coordinates are (a, b) and (c, d) is given by:
distance = √( (a - c)² + (b - d)²)
Here we can see that the coordinates of the two shown points are:
P = (-3, 2)
Q = (5, -1)
Replacing that in the distance formula we will get:
distance = √( (-3 - 5)² + (2 + 1)²)
distance = √( (-8)² + (3)²)
distance = √73
So the correct option is the third one.
Learn more about distance at:
https://brainly.com/question/7243416
#SPJ1