of the passengers on a 757 airliner, 40% are female. a random sample of 25 passengers is selected. what is the expected number of female passengers in the sample?
Answers
Therefore, the expected number of female passengers in the sample of 25 passengers is 10.
To find the expected number of female passengers in the sample, we can multiply the proportion of females in the population by the sample size.
Given that 40% of the passengers on a 757 airliner are female, the proportion of females is 0.40.
The sample size is 25 passengers.
Expected number of female passengers = Proportion of females * Sample size
Expected number of female passengers = 0.40 * 25
Expected number of female passengers = 10
To know more about expected number,
https://brainly.com/question/15393441
#SPJ11
Related Questions
im kinda confused on this. i need help.

Answers
Given :-
A graph is given to us .To Find :-
The equation in slope intercept form .Answer :-
From the given graph , we can see that the line passes through y axis at (0,5) . So the y intercept is 5 . And the slope of the line is 5/2 = 2.5 . So ,
\(\sf\longrightarrow\) y intercept = 5 .
\(\sf\longrightarrow\) slope = 5/2 .
Now here we can use the slope intercept form as ,
\(\sf\longrightarrow\) y = mx + c
\(\sf\longrightarrow\) y = 5/2x + 5
Hence the required answer is y = 5/2x + 5.
Answer:
y= 5/2x+5
Step-by-step explanation:
For an equation in slope intercept form we need the slope and the y-intercept. To find the y-intercept just look at which point touches the y-axis which is (0,5). To find the slope the equation is y2-y1 / x2-x1. We take two points that passes through the line like (-2,0) and (0,5). We plug the numbers in the equation which will be 5-0/ 0-(-2) = 5/2 as our slope.
Jessica's sister Deborah seems to only need six hours of sleep each night to be well rested. Jessica needs 8 hours most nights, but sometimes she
needs 9 or 10 hours to feel rested enough. How many hours of sleep should Jessica be getting EACH night?
O A. As many as Deborah
O B. No more than eight
O C. No less than 9 or 10
O D. Enough to feel rested
Answers
Answer:
The correct answer is D. Enough to feel rested.
Which of the following equations represents a line that is
perpendicular to
the y-axis and passes through the point (3, 12)
a x = 3
b x = 12
с y = 3
d y = 12
Answers
Answer:
cfc
Step-by-step explanation:
cfc
Answer:
3
Step-by-step explanation:
you suck
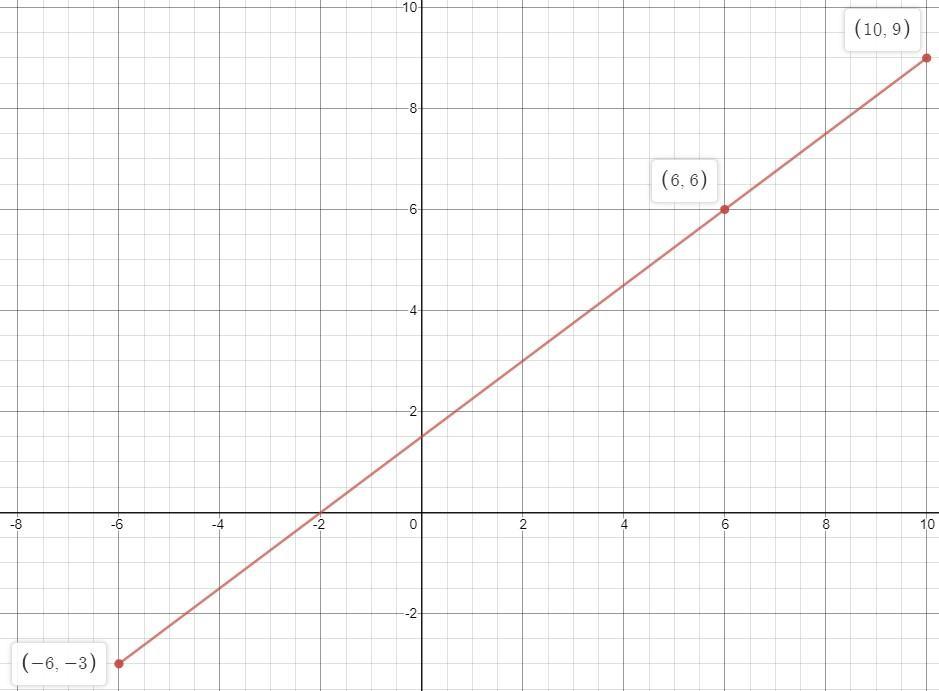
PLS HELP ME QUICK : What are the coordinates of the point ¾ of the way from A(−6, −3) to B(10, 9)?
Answers
Answer:
(6, 6)Step-by-step explanation:
Points given:
A(-6, -3) and B(10, 9)Coordinates of the point 3/4 of the way from the point A to B:
x = - 6 + 3/4(10-(-6)) = -6 + 3/4*16 = -6 + 12 = 6y = -3 + 3/4(9 -(-3)) = -3 + 3/*12 = -3 + 9 = 6(6, 6) is the point
What is the difference quotient for the function f (x) = negative startfraction 1 over 5 x minus 12 endfraction?
Answers
The difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
According to the given question.
We have a function
f(x) = -1/(5x -12)
As we know that, the difference quotient is a measure of the average rate of change of the function over and interval.
The difference quotient formula of the function y = f(x) is
[f(x + h) - f(x)]/h
Where,
f(x + h) is obtained by replacing x by x + h in f(x)
f(x) is a actual function.
Therefore, the difference quotient formual for the given function f(x)
= [f(x + h) - f(x)]/h
= \(\frac{\frac{-1}{5(x+h)-12} -\frac{-1}{5x-12} }{h}\)
= \(\frac{\frac{-1}{5x + 5h -12}+\frac{1}{5x-12} }{h}\)
= \(\frac{\frac{-1+5h}{5x + 5h-12} }{h}\)
= \(\frac{-1+5h}{(5x +h-12)(h)}\)
= \(\frac{-1+5h}{5xh + h^{2} -12h}\)
= \(\frac{h(-\frac{1}{h}+5) }{h(5x+h-12)}\)
= \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\)
Hence, the difference quotient of f(x) is \(\frac{-\frac{1}{h}+ 5}{5x+ h -12}\) .
Find out more information about difference quotient here:
https://brainly.com/question/18270597
#SPJ4
please help asp please

Answers
Answer:
C) 76 cm²
Step-by-step explanation:
area = (8 x 8 ) + (3 x 8 x 0.5) = 76 cm²
another way is:
area = 1/2(b1 + b2)(h)
area = 1/2(11 + 8)(8) = 76 cm²
Answer:
76
Step-by-step explanation:
Hello There!
The area can be found by using this formula
\(A=\frac{a+b}{2} h\)
where a and b = bases and h = height
we need to find the height before we can find the area
the shape was split into a triangle and a square
because its a square and one of the side lengths is equal to 8cm the height will be equal to 8cm
now we plug in the known information into the formula
\(A=\frac{11+8}{2} 8\\11+8=19\\\frac{19}{2} =8.5\\8.5*8=76\\A=76\)
so we can conclude that the area of the trapezoid is 76 square centimeters
I need help plz look at picture thx

Answers
The answer is G. N=2 (75) d
What is a possible third side to a triangle with side lengths of 13 and 4?
5
12
9
8
Answers
it will become obtuse triangle
115
11.5
Find the area of the shaded region

Answers
Answer:
227 units²
Step-by-step explanation:
Area of rectangle
a = (2 * 11.5) * (4 * 11.5)
a = 1,058
Area of circles
a = 2(π * 11.5²)
a = 830.9512568745
Shaded area
a = 1,058 - 830.9512568745
a = 227.0487431255
a ≈ 227
Mark invests $500 on a saving plan.The bank pays 5% interest each year on his investment. How much interest will he have after 2 years? (40 points NEED HELP WITH WORK PLS)
Answers
Answer:
551
Step-by-step explanation:
5% of 500 25
5 of 525 26.25
525+26.25
551.25
Sine interest formula: total = start amount x 1 + interest rate x time)
Total = 500 x (1+ 0.05 x 2)
Total = $550
Interest = 550 - 500 = $50
If an analysis of variance produces SS between = 20 and SS within = 40, then η 2 = 0.50.
true or false
Answers
Since η² ≈ 0.33 and not 0.50, the statement "If an analysis of variance produces SS between = 20 and SS within = 40, then η² = 0.50" is false.
ANOVA, or Analysis of Variance, is a statistical method used to compare the means of two or more groups to determine if there are any statistically significant differences between them. It is commonly used in experimental and observational studies to analyze the variance between group means and within-group variability.
ANOVA tests the null hypothesis that the means of the groups are equal, against the alternative hypothesis that at least one of the group means is different. It calculates the F-statistic, which compares the between-group variability to the within-group variability. If the F-statistic is large enough and exceeds a critical value, it indicates that there is evidence to reject the null hypothesis and conclude that there are significant differences between the group means.
We can determine if η² = 0.50 is true or false by calculating the effect size η² using the provided SS between and SS within values.
η² = SS_between / (SS_between + SS_within)
η² = 20 / (20 + 40)
η² = 20 / 60
η² = 1/3 ≈ 0.33
To know more about variance, visit:
https://brainly.com/question/31432390
#SPJ11
True, the eta-squared value is indeed 0.50, indicating that 50% of the total variance is accounted for by the between-group variation.
The formula to calculate eta squared (η2) is:
η2 = SSbetween / (SSbetween + SSwithin)
If SSbetween = 20 and SSwithin = 40, then:
η2 = 20 / (20 + 40) = 0.5
Therefore, η2 = 0.50, which means that 50% of the total variance in the dependent variable can be attributed to the independent variable (or factor) being analyze. The statement "If an analysis of variance produces SS between = 20 and SS within = 40, then η 2 = 0.50" is true. To determine η 2 (eta-squared), you'll need to calculate the proportion of total variance explained by the between-group variation. This can be done using the formula η 2 = SS between / (SS between + SS within). In this case, η 2 = 20 / (20 + 40) = 20 / 60 = 0.50. Therefore, the eta-squared value is indeed 0.50, indicating that 50% of the total variance is accounted for by the between-group variation.
To know more about variable visit:
https://brainly.com/question/15078630
#SPJ11
A rock is dropped from a bridge 128 feet above the river. The pathway that the rock takes can be modeled by the equation h= -16t2+128. How long will it take the rock to reach the river?
Answers
Answer:
2.83 seconds
Step-by-step explanation:
In the given equation, h represents the height (in feet) of the rock above the river at time t seconds after it is dropped, and the equation is h = -16t^2 + 128.
When the rock reaches the river, its height above the river will be zero. So, we can set h = 0 in the equation and solve for t:
0 = -16t^2 + 128
Dividing both sides by -16, we get:
t^2 = 128/16
t^2 = 8
Taking the square root of both sides, we get:
t = ±√8
Since time cannot be negative, we take the positive square root:
t = √8 ≈ 2.83 seconds
Therefore, it will take the rock approximately 2.83 seconds to reach the river.
Question 2: A line includes the points (20, 18) and (15, 13). What is its equation in
slope-intercept form?
y =
Answers
Answer:y=x
Step-by-step explanation: 13-18=-5
15-20=-5
-5/-5=1 slope
Using point slope take the first point and that slope to find the slope intercept.
Y-18=1(x-20)
Y=x-2
write 9/20 as a decimal
Answers
Answer:
0.45
Step-by-step explanation:
Divide 9 by 20.
The square pyramid at the entrance to the Louvre Museum in Paris, France, is 35.42 meters wide and 21.64 meters tall. Find the volume of the Louvre Pyramid.
Answers
Answer:
Step-by-step explanation:

Let C be the curve parameterized by r(t) = (5,3t, sin(2t)). Give parametric equations for the tangent line to the curve at the point (5,6phi,0).
Answers
Parametric equations for the tangent line to the curve at the point (5,6phi,0) are x = 5, y = 6φ + 3cos(2φ)(t − φ), and z = 3sin(2φ) + 2cos(2φ)(t − φ).
Given that curve C is parameterized by r(t) = (5, 3t, sin(2t))and we need to give parametric equations for the tangent line to the curve at the point (5, 6φ, 0).Firstly, to find the tangent line, we need to find the point on the curve where t = φ.So, we can say that r(φ) = (5, 3φ, sin(2φ)) is the point on the curve where t = φ.
Next, we find the derivative of the curve at t = φ, which is the tangent vector at that point, given by:r'(φ) = (0, 3, 2cos(2φ)).
Since we need the line passing through the point (5, 6φ, 0), the tangent vector is r'(φ), we can find the parametric equation of the tangent line by putting the values in the point-normal form of the equation of the plane, which is:x - x₁/a = y - y₁/b = z - z₁/c where (x₁, y₁, z₁) is the point on the plane and (a, b, c) is the normal vector to the plane.In this case, the point (5, 6φ, 0) lies on the tangent line, and the direction ratios of the tangent vector are (0, 3, 2cos(2φ)), so the parametric equation of the tangent line is:x = 5, y = 6φ + 3cos(2φ)(t − φ), and z = 3sin(2φ) + 2cos(2φ)(t − φ).
To know more about tangent line visit :-
https://brainly.com/question/23416900
#SPJ11
Could somebody help me? :((

Answers
Answer: Jenna multiplied both numbers by 5 and added the products of the two equations into her answer. Mia added the numbers then multiplied by 5 to get her answer. However, in some situations, this isn't the case. take 5(9+6) for example. You multiply both by 5 to get 45+30=75. That's correct. And when you add both to get 15, then multiplied by 5, you also get 75. But in certain scenarios, such as dividing, that won't be the case. 5(9/3)=15. (Dividing the 9 by 3 first) 5(9/30) [not dividing first] gets you 3.
Please help me out on any question, preferably all

Answers
11.) The measure of the interior angle of a regular decagon would be = 144°
How to calculate the interior angle of a decagon polygon?The total number of sides that a decagon polygon has = 10
The formula that is used to calculate the measure of interior angle of the decagon = (n-2) × 180/n
where n = number of sides = 10.
The measure of the interior angle of a regular decagon would be = (10-2)× 180/10
= 8×18 = 144°
Learn more about polygon here:
https://brainly.com/question/26583264
#SPJ1
Slide me number question 13 someone pls

Answers
The value of n from the given expression is y = (x-2)/z
Subject of formulaThe subject of formula is a way of representing a variable in terms of other variables.
Given the expression
x-2/y = z
Cross multiply
x - 2 = yz
Divide both sides by z
(x-2)/z = yz/z
(x-2)/z = y
Swap
y = (x-2)/z
Hence the value of n from the given expression is y = (x-2)/z
Learn more on subject of formula here: https://brainly.com/question/21140562
#SPJ1
Answer :
\(\frac{( x - 2 )}{z} = y\)
Step-by-step explanation:
\(\frac{(x-2)}{y} =z\)
Use cross multiplication.
\(( x - 2 ) = yz\)
Now, to make y the subject divide both sides by z.
\(\frac{( x - 2 )}{z} = y\)
For the given matrix A find a 3x2 matrix B such that AB=I, where I is the 2x2 identity matrix. [Hint: If B1 and B2 are the columns of B, then ABj = Ij.]
A =
1 2 1
1 1 1
Answers
For the given matrix A, a 3x2 matrix B such that AB=I, where I is the 2x2 matrix B = \(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}-2&1\\1&-1\\1&1\end{array}\right]\) when AB=I
Given matrix A = \(\left[\begin{array}{ccc}1&2&1\\1&1&1\\\end{array}\right]\)₂ₓ₃
B = \(\left[\begin{array}{ccc}1&2&1\\1&1&1\\\end{array}\right]\)₃ₓ₂
In such a way we know that, that AB = I ₂ₓ₂
therefore = \(\left[\begin{array}{ccc}1&2&1\\1&1&1\\\end{array}\right]\) \(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right]\)
we can say that \(\left[\begin{array}{ccc}a+2c+e&b+2d+f\\a+c+e&b+d+f\\\end{array}\right]\) = \(\left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right]\)
then, a+2c+e=1
then, when elaborated we get, a+2(-a-e)+e=1
a-2a-2e+e=1
-a-e=1
a+e = -1
2c-c = 1, c = 1 hence we get the value for c
similarly we can do the same steps for the other values
b+2d+f=0
1-d+2d=0
1+d = 0
d = -1
we get the value of d as well now for the value of a and e we can proceed as shown below:
a+c+e=0
c= -a-e
a+e= -c
a+e= -1
a= -2, e=1
similarly we can proceed as shownfor the values of b and f
b+d+f=1
b+f=1-d
b+f=2
b=1, f=1
when we put these values in the correct order and place we get the value for matrix b such as shown below,
therefore, matrix B = \(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}-2&1\\1&-1\\1&1\end{array}\right]\)
To learn more about matrix, click here:
brainly.com/question/28180105
#SPJ4
14) A contractor estimated that her expenses for a construction project would be between $700,000 and
$750,000 She has already spent $496.000 How much more can she spend and remain within her
estimate?
Write as an inequality!
Answers
Answer:
204000 < x < 254000
Step-by-step explanation:
700000 < 496000 + x < 750000
Solve for x by subtracting 496000 from both sides
204000 < x < 254000 ----> so we can conclude that she can spend between $204,000 and $254,000 more and remain within her estimate.
For the shape below, if side BD = 29 and side AC = 3x - 4, find x.

Answers
since sides BD and AC are congruent, then the equation would be 29=3x-4
Answer:
x = 11
Step-by-step explanation:
We know that the answer we will get will be the same as BD because BD and AC are congrudent, meaning that they are exactly equal shape and size. To find 'x' our equation would be: 29 = 3x - 4. To figure this out we just add 29 and 4 which gives us 33 and then divide that by 3 which gives us 11 (our answer)
10 feet wide and 15 feet long
Answers
Answer:
Area is 150
Step-by-step explanation:
data with 320 observations are drawn from a bell-shaped distribution with a mean of 62 and a standard deviation of 15. approximately how many observations are more than 92? (round your answer to the nearest whole number.)
Answers
Answer:
as 92 is 2 std deviaiton above mean ; th
Step-by-step expla
Find the slope and the equation of the tangent line to the graph of the function at the given value of x. y=x 4
−10x 2
+9;x=1 The slope of the tangent line is (Simplify your answer.) The equation of the tangent line is
Answers
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
The slope of the tangent line to the graph of the function y = x^4 - 10x^2 + 9 at x = 1 can be found by taking the derivative of the function and evaluating it at x = 1. The equation of the tangent line can then be determined using the point-slope form.
Taking the derivative of the function y = x^4 - 10x^2 + 9 with respect to x, we get:
dy/dx = 4x^3 - 20x
To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative:
dy/dx (at x = 1) = 4(1)^3 - 20(1) = 4 - 20 = -16
Therefore, the slope of the tangent line is -16.
To find the equation of the tangent line, we use the point-slope form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Given that the point of tangency is (1, y(1)), we substitute x1 = 1 and y1 = y(1) into the equation:
y - y(1) = -16(x - 1)
Expanding the equation and simplifying, we have:
y - y(1) = -16x + 16
Rearranging the equation, we obtain the equation of the tangent line:
y = -16x + (y(1) + 16)
To find the slope of the tangent line, we first need to find the derivative of the given function. The derivative represents the rate of change of the function at any point on its graph. By evaluating the derivative at the specific value of x, we can determine the slope of the tangent line at that point.
In this case, the given function is y = x^4 - 10x^2 + 9. Taking its derivative with respect to x gives us dy/dx = 4x^3 - 20x. To find the slope of the tangent line at x = 1, we substitute x = 1 into the derivative equation, resulting in dy/dx = -16.
The slope of the tangent line is -16. This indicates that for every unit increase in x, the corresponding y-value decreases by 16 units.
To determine the equation of the tangent line, we use the point-slope form of a linear equation, which is y - y1 = m(x - x1). We know the point of tangency is (1, y(1)), where x1 = 1 and y(1) is the value of the function at x = 1.
Substituting these values into the point-slope form, we get y - y(1) = -16(x - 1). Expanding the equation and rearranging it yields the equation of the tangent line, y = -16x + (y(1) + 16).
The equation of the tangent line represents a straight line that passes through the point of tangency and has a slope of -16.
To learn more about tangent click here:
brainly.com/question/10053881
#SPJ11
Jonshon attempted 73 shots and made 34 while clarence attempted 52 and made 28. Which player has the high scoring percentage?
Answers
Johnson has a scoring percentage of 46.57% while Clarence has a scoring percentage of 53.84%. Clarence has the higher scoring percentage.
A percentage is a way of expressing a number as a fraction of 100. It is often used to represent a part of a whole or a comparison between two quantities.
To calculate the scoring percentage, we divide the number of shots made by the number of shots attempted and then multiply by 100. For Johnson, the scoring percentage is
(34/73)*100 = 46.57%.For Clarence, the scoring percentage is
(28/52)*100 = 53.84%.Therefore, Clarence has the higher scoring percentage.
Learn more about Percentage:
https://brainly.com/question/24877689
#SPJ4
Giving brainliest! Please give me the working out for the answer

Answers
Answer:
∠BCD is a right angle ⇒ Proved down
Step-by-step explanation:
Let us revise some fact in the circle
If the vertices of a quadrilateral lie on a circumference of a circle, then this quadrilateral is called a cyclic quadrilateral In a cyclic quadrilateral, every two opposite angles are supplementary (the sum of their measures is 180°)Let us use these facts to solve the question
∵ ABCD is a quadrilateral
∵ Its vertices lie of the circumference of the circle
∴ ABCD is a cyclic quadrilateral
By using the facts above
∴ ∠ABC and ∠ADC are supplementary
∴ m∠ABC + m∠ADC = 180° → (1)
∵ m∠ABD = m∠CBD → given
∵ m∠ABC = m∠ABD + m∠CBD
∴ m∠ABC = 2m∠CBD → (2)
∵ m∠ADB = m∠CDB → given
∵ m∠ADC = m∠ADB + m∠CDB
∴ m∠ADC = 2m∠CDB → (3)
→ Substitute (2) and (3) in (1)
∴ 2m∠CBD + 2m∠CDB = 180
→ Divide both sides by 2
∴ m∠CBD + m∠CDB = 90
In ΔBCD
∵ m∠BCD + m∠CBD + m∠CDB = 180 → Sum of angles of a triangle
∵ m∠CBD + m∠CDB = 90
∴ m∠BCD + 90 = 180
→ Subtract 90 from both sides
∴ m∠BCD + 90 - 90 = 180 - 90
∴ m∠BCD = 90°
∴ ∠BCD is a right angle ⇒ proved
Helpp me plssssss????

Answers
Answer:
C
Step-by-step explanation:
The radius is 4 making the diameter 16 you need the other side since in half so that leaves you with answer C...16\(\pi yd^2\)
There is 30 points to whoever can figure this out

Answers
the graph of two functions g ( x ) and f ( x ) are shown below

Answers
If g(x) = f(x) + k, then, the value of k will be 3.
Define functions.There are eight distinct types of frequently employed functions, and therefore eight distinct forms of function graphs. Linear, power, quadratic, polynomial, rational, exponential, logarithmic, and sinusoidal function graphs fall under this category. To establish if a graph reflects a function, use the vertical line test. The graph is a function if a vertical line drawn across it is moved and only ever touches it at one point. The graph is not a function if the vertical line crosses it at more than one location.
Given,
The graph of the two functions is given,
If g(x) = f(x) + k
Then, the value of k will be 3.
To learn more about function, visit:
https://brainly.com/question/28278690
#SPJ1