On a sunny day, a 15-foot pole casts a 20-foot long shadow, how tall is a person who casts a 8 foot shadow (Draw an image to help you solve the problem). O 10 6 feet O 6 feet O 375 feet O B feet None of the above
Answers
The image can be drawn as,
The height of the person can be determined as,
\(\begin{gathered} \tan C=\frac{AB}{CB}=\frac{DE}{CE} \\ \frac{AB}{CB}=\frac{DE}{CE} \\ \frac{15}{20}=\frac{DE}{8} \\ DE=\frac{15\times8}{20} \\ DE=6\text{ ft} \end{gathered}\)Thus, the required height of the man is 6 ft.

Related Questions
5. Given the right triangle JKL, identify the locations of sides j, k, and I in relation to angle L
in terms of opposite, adjacent, and hypotenuse.
HELP

Answers
In relation to the angle L of the right triangle the sides are as follows:
l = opposite sidek = hypotenusej = adjacentHow to name the side of a right triangle?A right angle triangle is a triangle that has one of its angles as 90 degrees. The sides of a right angle triangle can be named according to the position of the angles in the right angle triangle.
The sides of a right triangle can also be solved by using Pythagoras's theorem or trigonometric ratios.
Let's identify the sides j, k, and I in relation to angle L in terms of opposite, adjacent, and hypotenuse.
Therefore,
l = opposite sidek = hypotenusej = adjacentThe hypotenuse side is the longest side of a right triangle.
learn more on right triangle here: https://brainly.com/question/17810121
#SPJ1
What’s the correct answer for this?

Answers
Answer:
B:
Step-by-step explanation:
IN THE ATTACHED FILE

4tan(x)-7=0 for 0<=x<360
Answers
Answer:
x = 65.26 degrees or x = 245.26 degrees.
Step-by-step explanation:
To solve the equation 4tan(x)-7=0 for 0<=x<360, we can first isolate the tangent term by adding 7 to both sides:
4tan(x) = 7
Then, we can divide both sides by 4 to get:
tan(x) = 7/4
Now, we need to find the values of x that satisfy this equation. We can use the inverse tangent function (also known as arctan or tan^-1) to do this. Taking the inverse tangent of both sides, we get:
x = tan^-1(7/4)
Using a calculator or a table of trigonometric values, we can find the value of arctan(7/4) to be approximately 65.26 degrees (remember to use the appropriate units, either degrees or radians).
However, we need to be careful here, because the tangent function has a period of 180 degrees (or pi radians), which means that it repeats every 180 degrees. Therefore, there are actually two solutions to this equation in the given domain of 0<=x<360: one in the first quadrant (0 to 90 degrees) and one in the third quadrant (180 to 270 degrees).
To find the solution in the first quadrant, we can simply use the value we just calculated:
x = 65.26 degrees (rounded to two decimal places)
To find the solution in the third quadrant, we can add 180 degrees to the first quadrant solution:
x = 65.26 + 180 = 245.26 degrees (rounded to two decimal places)
So the solutions to the equation 4tan(x)-7=0 for 0<=x<360 are:
x = 65.26 degrees or x = 245.26 degrees.
what is the maths formula for area
Answers
Answer:
Quick internet search:


On my farm there are 10 brown horses and 8 mares(female horses).Can you conclude that there are 18 horses on my farm
Answers
Answer:
Yes
Step-by-step explanation:
You can conclude there are 18 horses because although some of the mares might be brown horses, the conjunction "and" implies the mares are in addition to the brown horses.
Find two vectors v1 and v2 whose sum is (0, -1, -3), where v1 is parallel to (5, 0, -4) while v2 i perpendicular to (5, 0, -4).
v1 = ?
v2 = ?
Answers
Two vectors v₁ and v₂ whose sum are (0, -1, -3), where v₁ is parallel to
(5, 0, -4) while v₂ is perpendicular to (5, 0, -4).
v1 = [40/13, -8/13 ]
v2 = [-1/13, -5/13]
Parallel vectors will be multiples of each other.
Perpendicular vectors will have a dot product of 0.
Let v₁ = [a, b] and v₂ = [c, d]
v₁ || [-5,1] means v₁ = N [-5,1] = [a, b]
So a = -5N and b = N
v₂ • [-5,1] = 0 (because they are perpendicular)
So [c, d] • [-5,1] = -5c + d = 0 or d = 5c
⇒ v₁ + v₂ = [a, b] + [c, d] = [3, -1]
So a + c = 3 and b + d = -1
Now,
Substitute -5N for
a. Substitute N for b.
and Substitute 5c for d.
This gives us a system of equations with two equations and 2 unknowns:
-5N + c = 3
N + 5c = -1
Multiply everything in the bottom equation by 5
-5N + c = 3
5N + 25c = -5
Now add vertically, eliminating the variable N and finding
26c = -2
or, c = -1/13
Now we work our way backwards.
-5N + c = -5N + (-1/13) = 3
-5N = 40/13
(-1/5) (-5N) = (40/13)(-1/5)
and
N = -8/13 and b = N so b = -8/13
d = 5c so d = -5/13
a = -5N, so a = 40/13
So the two vectors are:
v₁ = [40/13, -8/13 ]
v₂ = [-1/13, -5/13]
Learn more about Perpendicular:
https://brainly.com/question/29268451
#SPJ4
Hey can someone please help me with this

Answers
x = -2
The graph is the top one on the left.
Which equation shows the
commutative property of addition?
A 2x = 2x
B 2x + 3 = 3 + 2x
C 2x - 3 = 2(x - 3)
D 2(x + 3) = 2x + 6
Answers
Answer:
B
Step-by-step explanation:
Have a nice day!
How to calculate Standard Error of the Y intercept and standard error of the slope, given the table below, without the SE coefficient given.

Answers
Answer:
Step-by-step explanation:
the stabdard error is given with the se coefficient snf the y slope
evaluate the expression for h= -6.

Answers
Answer:
63-|-6| = 57
Step-by-step explanation:
63-|-6|
63-6
57
Answer:
57
Step-by-step explanation:
Substitute -6 for variable h.
\(63-|(-6)|\\63-6\\57\)
Question 14 5 pts Starting with the geometric series Eaz 0 (~1)"z which of the following is the sum of the series Xac-2 n (n ~ 1) (~1)" I2"-2 for Ixl < 1? (1+) x(x x" (1
Answers
The sum of the geometric series for Xac-2 n\((n ~ 1) (~1)" I2"-2 for Ixl < 1 is (1 - x2)\). This is because the series is a summation of the terms (1/x2) multiplied by each power of x from 0 to n, and the sum of the series is the sum of the terms.
To calculate the sum of the geometric series for\(Xac-2 n (n ~ 1) (~1)" I2"-2 for Ixl < 1\), we can use the formula for the sum of a geometric series. The sum of such a series is the sum of the terms (1/x2) multiplied by each power of x from 0 to n. Thus, the sum of the series is given by the formula S = (1/x2) ∑ xn, where n starts at 0 and goes to n. Substituting n = -2 and x = 1 gives us S = (1/1) ∑ 1-2, which simplifies to S = (1/1) (1 - 1-2) = (1 - 1-2) = (1 - x2). Hence, the sum of the series is (1 - x2).
Learn more about geometric series here
https://brainly.com/question/21087466
#SPJ4
Find the surface area
of the figure below:
19 cm
30 cm.

Answers
The surface area of the figure is approximately 997.5π cm².
We have,
The figure has two shapes:
Cone and a semicircle
Now,
The surface area of a cone:
= πr (r + l)
where r is the radius of the base and l is the slant height.
Given that
r = 15 cm and l = 19 cm, we can substitute these values into the formula:
= π(15)(15 + 19) = 885π cm² (rounded to the nearest whole number)
The surface area of a semicircle:
= (πr²) / 2
Given that r = 15 cm, we can substitute this value into the formula:
= (π(15)²) / 2
= 112.5π cm² (rounded to one decimal place)
The surface area of the figure:
To find the total surface area of the figure, we add the surface area of the cone and the surface area of the semicircle:
Now,
Total surface area
= 885π + 112.5π
= 997.5π cm² (rounded to one decimal place)
Therefore,
The surface area of the figure is approximately 997.5π cm².
Learn more about cones here:
https://brainly.com/question/13798146
#SPJ1
Value 2000 is decresed to 100. What is the percent decreased
Answers
Answer:
PD = 95%
Step-by-step explanation:
(2,000 - 100) / 2,000 times 100
( (original - new) ) / original times 100
= 1,900 / 2,000 times 100
= 0.95 times 100
= 95% decrease
Step-by-step explanation:
please help w this i don’t get it :(

Answers
Answer:80°
This is the answer i think hope this helps you
Factor 15cd − 45c2d.
3c2d(5 − 15)
5cd(3 − 15c2d)
3cd(5 − 15c)
5cd(3 − 45c2d)
Answers
Answer:
C
Step-by-step explanation:
The given expression is illustrated as:
15cd-45c2d
This will be:
15cd-45c2d = 3cd(5-15c)
Note: It is important to note that factors are the numbers that divide evenly into another number that is given.
I need urgent help with this pls

Answers
Anna counted the number of articles in several different magazines. Number of articles Number of magazines 17 5 23 4 27 3 29 3 36 3 46 2 X is the number of articles that a randomly chosen magazine had. What is the expected value of X? Write your answer as a decimal. Submit O Type here to search o
Answers
Expected value is found by
Sum of x• f(x) = ( 5•17 + 4•23 + 3•27+ 3•29+3•36 + 2•46 ) =
. = 85 + 92 + 81 + 87 + 108 + 92= 545
divided by number of magazines
Then answer is
Expected value = 545/20 = 27 articles
f(x) = 6^2+12x -7
please answer and explainnnn!

Answers

Answer:
A) \(x=-1\pm\sqrt{\frac{13}{6}}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-12\pm\sqrt{12^2-4(6)(-7)}}{2(6)}\\\\x=\frac{-12\pm\sqrt{144+168}}{12}\\\\x=\frac{-12\pm\sqrt{312}}{12}\\\\x=\frac{-12\pm2\sqrt{78}}{12}\\\\x=-1\pm\frac{\sqrt{78}}{6}\\\\x=-1\pm\sqrt{\frac{78}{36}}\\\\x=-1\pm\sqrt{\frac{13}{6}}\)
please help solve and justify answer

Answers
The car that drove off had a year of manufacture of 2013. However, this answer does not make sense, as all of the given cars were manufactured before 2010 and was solved by using mean.
What is mean?In mathematics, the mean is a measure of central tendency of a set of numbers. It is commonly referred to as the average and is calculated by adding up all the numbers in a set and dividing by the total number of numbers in the set.
In the given question,
Let's start by finding the mean of the five cars:
Mean = (1971 + 1986 + 1993 + 2003 + 2010) / 5 = 1992.6
Now, let's assume that one of the cars drove off and we need to find out which one. Let's call the year of manufacture of the car that drove off "x".
If the mean of the remaining four cars is 1990, we can use the formula for the mean of a set of numbers to set up an equation:
(1971 + 1986 + 1993 + 2003 + 2010 - x) / 4 = 1990
Simplifying this equation, we get: (9973 - x) / 4 = 1990
Multiplying both sides by 4, we get: 9973 - x = 7960
Subtracting 9973 from both sides, we get: -x = -2013
Dividing both sides by -1, we get: x = 2013
Therefore, the car that drove off had a year of manufacture of 2013. However, this answer does not make sense, as all of the given cars were manufactured before 2010. Therefore, we can conclude that there was a mistake in the problem, or that the problem was poorly worded. Without additional information, we cannot determine which car drove off.
To Know more about mean, visit:
https://brainly.com/question/31098693
#SPJ1
please help me!!!!!!!!!!

Answers
Answer:
HFHBEHFBHEHHEHHHHH
Step-by-step explanation:
Can y’all tell me which one is a function and which ones is not ?

Answers
the ones with straight lines are functions the ones that are curved is not a function
Answer:
Ones that have 2 values of y for a single value of x
(vertical line, sideways v shape are not functions)
Step-by-step explanation:
In a function, each input (x) can have only one output (y)
There cannot be two ys for one x
Select the correct answer.
68600
A) 6.86 × 104
C) 0.686 × 10²
B) 0.686 × 10¹
D) 6.86 x 10²
Answers
Answer:
A) 6.86×10⁴
Step-by-step explanation:
You want to write 68600 in scientific notation.
Expanded formThe number 68600 can be written in expanded form with exponents as ...
68600 = 6×10⁴ +8×10³ +6×10² +0×10¹ +0×10⁰
The left-most term of this sum tells you the exponent in scientific notation:
68600 = 6.86×10⁴

Can somebody give me an answer? ill give brainiest.
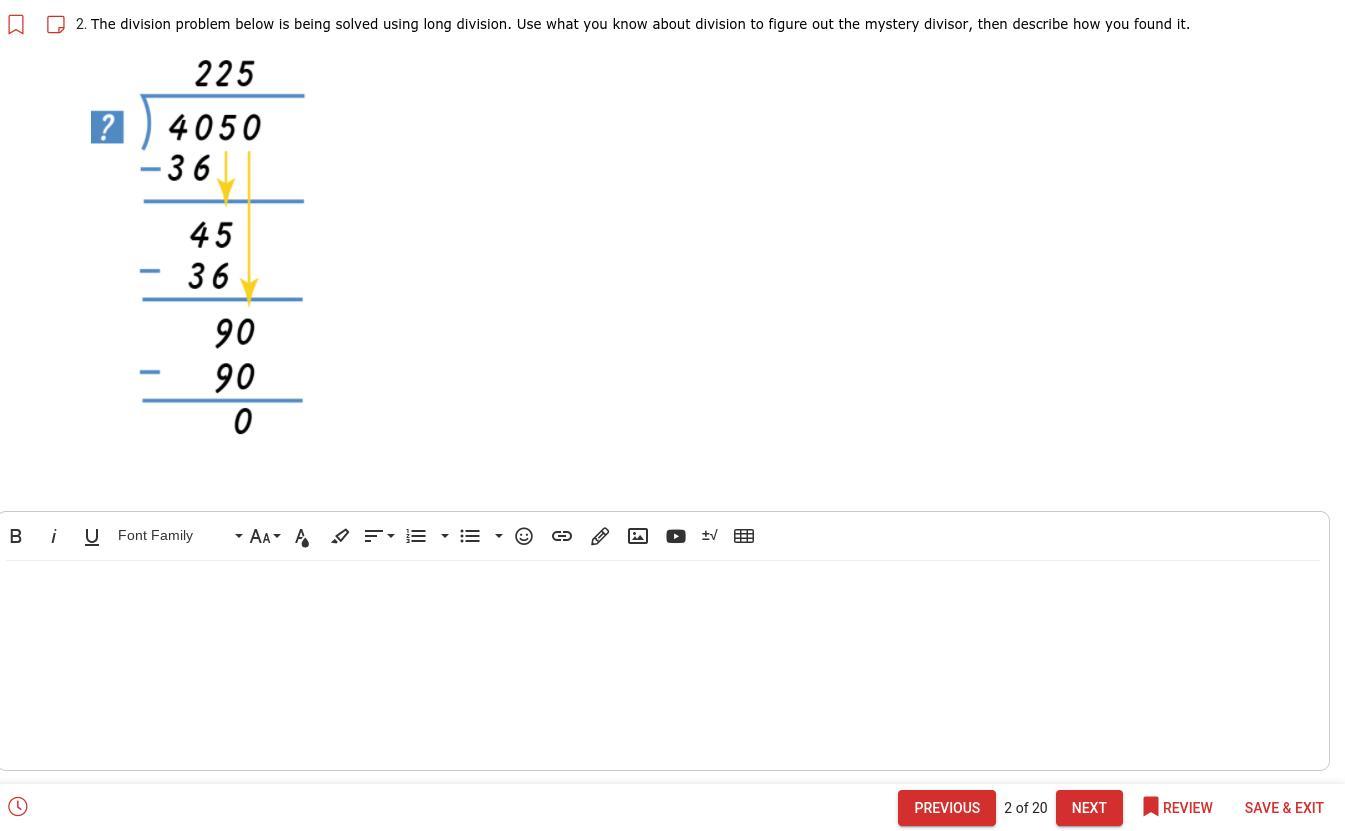
Answers
Answer:
The mystery divisor is 18
Step-by-step explanation:
In the beginning, I found it by simply dividing the dividend by the quotient which gave me the divisor of 18. You can start the division equation again and add in the divisor 18 and it'll give you the exact answer.
Another way you'll know it's correct, is by dividing the dividend by that divisor and it'll give you the quotient 225 just like in the image.
What is the degree of the polynomial, y^2+7x^14-10x^2?
Answers
The degree of the polynomial is 14
How to determine the degree of the polynomial?The polynomial is given as:
y^2+7x^14-10x^2
Here, we assume that the variable of the polynomial is x
The highest power of x in the polynomial y^2+7x^14-10x^2 is 14
Hence, the degree of the polynomial is 14
Read more about polynomial at
https://brainly.com/question/4142886
#SPJ1
In a class test, +4 marks were awarded for the correct answers and -1 mark for the wrong answers. Student scores 40 marks. If his correct answers were 11, find his wrong answers.
Answers
Step-by-step explanation:
Let y the number of wrong answers got.
\(11( + 4) + ( - 1)y = 40 \\ 44 - y = 40 \\ - y = - 4 \\ y = 4\)
∴ He got 4 wrong answers.
Find the area of the shape

Answers
Hello!
area
= 2*25 + (20 - 2)*(25-8)
= 50cm² + 306cm²
= 356cm²
Describe the shape of the data represented below.

Answers
The shape of the data that we have here is skewed to the right
How is a data skewed to the right?A dataset is considered to be right-skewed (sometimes known as excessively positive) when the greater portion of its data points are concentrated on the lower end, forming an asymmetrical distribution that has a long tail to the right.
As such, the mean (average) within these distributions generally surpasses the median in value, with the latter also exceeding the mode.
Read more on Skewness here:https://brainly.com/question/30054635
#SPJ1
find the measure of the indicated angle to the nearest degree. Show the work please.

Answers
Answer: 1) 65° 2) 17° 3) 53° or 37°
Step-by-step explanation:
\(1.\quad \cos \theta=\dfrac{adjacent}{hypotenuse}\\\\\\.\quad \quad \cos \theta=\dfrac{3}{7}\\\\\\.\qquad \qquad \theta=\cos ^{-1}\bigg(\dfrac{3}{7}\bigg)\\\\\\.\qquad \qquad \theta =65^o\)
\(2.\quad \tan \theta =\dfrac{opposite}{adjacent}\\\\\\.\quad \quad \tan\theta =\dfrac{8}{26}\\\\\\.\qquad \qquad \theta =\tan ^{-1}\bigg(\dfrac{4}{13}\bigg)\\\\\\.\qquad \qquad \theta = 17^o\)
3. Which angle do you need? I solved for both:
Bottom Right Top Left
\(.\qquad \cos \theta=\dfrac{adjacent}{hypotenuse}\qquad \qquad \sin \theta = \dfrac{opposite}{hypotenuse}\\\\\\.\quad \quad \cos \theta=\dfrac{14}{23}\qquad \qquad \qquad \qquad \sin \theta=\dfrac{14}{23}\\\\\\.\qquad \qquad \theta=\cos ^{-1}\bigg(\dfrac{14}{23}\bigg)\qquad \qquad \quad \theta=\sin ^{-1}\bigg(\dfrac{14}{23}\bigg)\\\\\\.\qquad \qquad \theta =53^o\qquad \qquad \qquad \qquad \quad \theta =37^o\)
Question 1:
cosθ = adj/hyp
cosθ = 3/7
θ = cos^-1(3/7)
θ = 65
Questions 2:
tanθ = opp/adj
tanθ = 8/26
θ = tan^-1(4/13)
θ = 17
Question 3:
Top left:
sinθ = opp/hyp
sinθ = 14/23
θ = tan^-1(14/23)
θ = 37
Bottom Right:
cosθ = adj/hyp
cosθ = 14/23
θ = cos^-1(14/23)
θ = 53
Best of Luck!
Find the perimeter and area of rectangle ABCD if each unit on the graph measures 1 centimeter. Round answers to the nearest tenth, if necessary.

Answers
The perimeter of the rectangle ABCD is 22.34 units and the area of the rectangle ABCD is 29.95 square units
The points are given A(-2,7), B(4,4), C(2,0) and D(-4,3)
First we have to find the distance between the points
The distance between two points = \(\sqrt{(x_{2}-x_{1})^{2}+(y_{2} -y_{1} )^{2} }\)
The distance between A and B = \(\sqrt{(4-(-2))^{2}+(4-7))^{2} }\)
= \(\sqrt{36+9 }\)
= 6.70 units
The distance between BC =\(\sqrt{(2-4)^{2}+(0-4)^{2} }\)
= \(\sqrt{4+16}\)
=4.47 units
The distance between A and B = The distance between C and D
The distance between C and C = The distance between D and A
The perimeter of the rectangle = 2(l+w)
Where l is the length and w is the width of the rectangle
The perimeter of the rectangle = 2(6.70+4.47)
=22.34 units
The area of the rectangle = l×w
= 6.70×4.47
=29.95 square units
Hence, the perimeter of the rectangle ABCD is 22.34 units and the area of the rectangle ABCD is 29.95 square units
Learn more about distance between two points here
brainly.com/question/24485622
#SPJ1
what is the slope that passes through the points (2,8) and (4,4)
Answers
Answer:
-2
Step-by-step explanation:
m = -4 / 2 = -2 / 1 = -2
Your function:
The entered points belong to a decreasing, linear function.
Equation: y = -2x + 12.
Related numbers
Y - intercept
12
Angle (θ)
-63.43
deg
θ = arctan(-2) = -6.34349
Percentage grade
-200%
Distance (d)
4.472
Distance between x's (Δx)
2
Distance between y's (Δy)
4
d = √(Δy2 + Δx2) = √(-42 + 22) = √20 = 4.47214