Pablo finished his history assignment in 3/4 hours. Then he completed his math assignment in 1/5 hours. What was the total amount of time Pablo spent doing these two assignments? Write your answer as a fraction in simplest form.
Answers
The total amount of time Pablo spent doing both assignments is 19/20 hours.
How to calculate how much time did Pablo spend on these two assignments in total?To find the total amount of time Pablo spent doing both assignments, we need to add the time he spent on each one.
Time spent on history assignment = 3/4 hours
Time spent on math assignment = 1/5 hours
Total time = 3/4 + 1/5
We need to find a common denominator for the two fractions, which is 20.
3/4 = 15/20
1/5 = 4/20
Now we can add them:
15/20 + 4/20 = 19/20
Therefore, the total amount of time Pablo spent doing both assignments is 19/20 hours.
Learn more about fraction at https://brainly.com/question/78672
#SPJ1
Related Questions
Drag each tile to the correct box.
Match each equation with its solution.
n =
= -1
n = -25
n = 1
Equation
Solution
12 + 15 = -10
>
-511 = 1
- 13 = -12
Answers
Answer:
n = 1
n = - 1
n = - 1/5
n = - 25
Step-by-step explanation:
We are to obtain the value if n in the given equations :
1.)
n - 13 = - 12
To find, n ;
Add 13 to both sides
n - 13 + 13 = - 12 + 13
n = 1
2.)
n/5 = - 1/5
Multiply both sides by 5
n/5 * 5 = - 1/5 * 5
n = - 1
3.)
-5n = 1
Divide both sides by - 5
-5n/-5 = 1/-5
n = - 1/5
4.)
n + 15 = - 10
Subtract 15 from both sides :
n + 15 - 15 = - 10 - 15
n = - 25

What is the meaning of "The usual notation makes this identification transparent by writing every sequence (x1, x2, ..., xn) as a product or word x1x2· · · xn in the alphabet X"?

Answers
The statement refers to the way that symbols are represented in sequences, a common practice in formal language theory, by employing a notation that makes symbols a part of the sequence.
How is sequence notation and language related?In formal language theory, a language is often defined as a set of strings over an alphabet. By representing any alphabetic sequence of symbols as a single string using the notation outlined in the statement, we are able to recognise the language that comprises that sequence as a collection of strings. A subset of the language having all possible strings over the alphabet (a, b, and c) is the set of strings abc, which may be used to represent the language including the sequence (a, b, and c). So, this notation offers an easy approach to discuss languages and the sequences that make up such languages.
Hence, the statement relates the symbols and sequences.
Learn more about sequence here:
https://brainly.com/question/21961097
#SPJ1
XYZ Company
Balance Sheet
Assets
Cash
$45,000
Inventory $41,000
Property $134,000
Total Assets:
Liabilities
Notes
Wages
Equity
Stock
$55,000
$56,000
$50,000
Investment $59,000
Total Liabilities + Equity:
Using the balance
sheet, calculate XYZ
Company's total
assets - liabilities.
Total Assets - Liabilities = $ [?]
Enter
PH
Skip
Answers
Answer:
To calculate XYZ Company's total assets minus liabilities, you would need to add up all of the assets listed on the balance sheet and then subtract the sum of all the liabilities.
In this case, the total assets would be $45,000 + $41,000 + $134,000 = $220,000. The total liabilities would be $55,000 + $56,000 + $50,000 = $161,000.
So, the total assets minus liabilities would be $220,000 - $161,000 = $59,000.
Step-by-step explanation:
Solve for angles x and y in the triangle below. Round your angle to the nearest whole degree.
Solve for both x and y

Answers
\(\tan(y )=\cfrac{\stackrel{opposite}{6}}{\underset{adjacent}{4}} \implies \tan( y )= \cfrac{3}{2} \implies \tan^{-1}(~~\tan( y )~~) =\tan^{-1}\left( \cfrac{3}{2} \right) \\\\\\ y =\tan^{-1}\left( \cfrac{3}{2} \right)\implies y \approx 56.31^o \\\\[-0.35em] ~\dotfill\\\\ \tan(x )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{6}} \implies \tan( x )= \cfrac{2}{3} \implies \tan^{-1}(~~\tan( x )~~) =\tan^{-1}\left( \cfrac{2}{3} \right) \\\\\\ x =\tan^{-1}\left( \cfrac{2}{3} \right)\implies x \approx 33.69^o\)
Make sure your calculator is in Degree mode.
Choose the expression that correctly compares the numbers 117 and 171.
171 < 117
171 = 117
171 > 117
117 > 171
Answers
Answer:
171 > 117
Step-by-step explanation:
171 is greater than 117 meaning the alligator is eating the bigger number, 171.
PLS HELP ME !!!!!!!!!!!!!!!!

Answers
Answer:
C
Step-by-step explanation:
All sides make a cube
Answer:
D
Step-by-step explanation:

Now you try on your own.
Kelly wants to build a new wardrobe for herself with only clothing pieces she loves, fit her well, and coordinate together. She already has most of the pieces she will use, but needs to save up to go shopping for the remaining items. She has already saved some money from her job, and she decides to set aside money weekly from her tips. The expression $25w+$65
represents the amount of money Kelly will have saved after some amount of weeks. What does each part of this expression represent?
$25=
Answer
w=
Answer
$65=
Answer
For this specific expression, would it make sense to plug in a negative number for w
? Answer
For this specific expression, would you ever expect to get a number less than 65
for your total amount saved?

Answers
The Interpretatiom of the equation is that;
w represents number of weeks she will have saved for the remaining items
$25 represents the amount she saves per week
$65 represents the amount she has already saved
How to solve algebra word problems?The algebra word problem can be solved by using variables to denote certain parameters I'm the question.
The general form of equation of a line in slope intercept form is;
y = mx + c
Where;
m is slope
c is y-intercept
We are given the equation:
$25w + $65
This equation represents the amount of money Kelly will have saved after some amount of weeks.
Thus;
w represents number of weeks she will have saved for the remaining items
$25 represents the amount she saves per week
$65 represents the amount she has already saved
Read more about Algebra Word problems at; https://brainly.com/question/21405634
#SPJ1
What is the missing length??

Answers
Answer
The missing length is 10
Step-by-step explanation:
Represent the missing length with x
The sides of the given shape are directly proportional.
Mathematically:
(15 + x) to (12 + 8) and x to 7
Represent as a ratio:
\((15 + x) : (12 + 8) = x : 8\)
\(15 + x : 20= x : 8\)
Convert to fraction
\(\frac{15 + x}{20} = \frac{x}{8}\)
Cross Multiply:
\((15 + x)*8 = 20 * x\)
\(120 + 8x = 20x\)
Collect Like Terms
\(20x - 8x = 120\)
\(12x = 120\)
Solve for x
\(x = \frac{120}{10}\)
\(x = 10\)
The length of the missing side is 10
I need help how do I solve this?

Answers
The answer is just -infinite
can someone help me pleasee

Answers
The polynomial of degree 4, P(x), can be written as a product of linear factors in the form of P(x) = a(x-4)²(x-0)(x+4) where a is a constant.
What is value?Value of subjective concept that refers to the word of important that an individual group of people places on the something it is often associated with principal beliefs and the standard that are accepted by society when you can be seen as a matter of how important something is true person of organization it is often seen as a reflection of funds for view and can help to save decision.
To find the value of a, we can use the point (5,18) which is given. Since P(5) = 18, we can substitute 5 for x in the equation and solve for a. This gives us a (5-4)²(5-0)(5+4) = 18, and we can solve for a = 18/120 = 0.15. Therefore, the formula for P(x) is P(x) = 0.15(x-4)²(x-0)(x+4).
To know more about value click-
https://brainly.com/question/25184007
#SPJ1
Which expression is equivalent to (3−22)+5?
All the Second 2s are exponent
5−22
22−5
5−32
32−5
Answers
Answer:
3²-5
Step-by-step explanation:
(3-2²)+5=4
3²-5=4
Answer:
D
Step-by-step explanation:
First off, lets simplify (3-2^2)+5 = -1+5 = 4
We will need to find an expression that will equal to 4
lets try 1, 5-2^2 = 1, 1 =\ 4
Alright, lets try 2, 2^2 -5 = -1, -1=\5
Now lets try 3, 5 - 3^2 = -4, -4=\4
So by process of elimination we can say that D is correct by I will show you why it is correct. 3^2 -5 = 4, 4=4
If you have any questions ask me.
Hope it helped :)
Write the Roman Numeral CXXXIV in standard???
Answers
Answer:
Step-by-step explanation: C is 100 X is 10 IV is 4 since the smaller number is in the front so you subtract instead of add
C=100 3X=30 IV=4
100+30+4=134
CXXXIV=134
11. Suppose a force F varies as the product of two masses, m and M, inversely as
the square of the distance r between them. If F= 675 when m = 125, M = 225,
and r=0.0530, find the constant of proportionality k.
A. 61.48 X 10-10
B. 1.27X10-
C. 6.74 x 10-5
D. 6.76X10°
E. None
Answers
Answer:
\(k = 6.74 * 10^{-5}\)
Step-by-step explanation:
Given
\(F\ \alpha\ \frac{m * M}{r^2}\) --- The variation
\(F = 675; m = 125; M = 225; r = 0.0530\)
Required
Determine the constant of proportionality (k)
\(F\ \alpha\ \frac{m * M}{r^2}\)
Express as an equation
\(F = k\frac{m * M}{r^2}\)
Multiply both sides by \(r^2\)
\(Fr^2 = km * M\)
Make k the subject
\(k = \frac{Fr^2}{m * M}\)
Given that: \(F = 675; m = 125; M = 225; r = 0.0530\)
We have:
\(k = \frac{675* 0.0530^2}{125 * 225}\)
\(k = \frac{1.896075}{28125}\)
\(k = 0.000067416\)
This can be represented as:
\(k = 6.74 * 10^{-5}\)
Please help my cousin do this. She isn't that bright in math.

Answers
Answer:
$4.8 for sugar and $25 for butter.
Step-by-step explanation:
Angle ADB and CD are straight lines. angle ADC = 5 x angle CDB Work out the size of angle ADC.

Answers
Answer:
Step-by-step explanation:

What is the solution to the following system of equations? A: (-2,3) B: (3, 1)C: (3, -2)D: (1, -3)


Answers
The graph shows the lines of two equations, a blue line and a red line.
Note that to solve a system of equations graphically, we would need to identify the point at which they both intersect.
The lines of these two equations intersect at the point where x = -3 and y = 1
ANSWER:
\((-3,1)\)The correct answer is option B
The net of a rectangular prism and its dimensions are shown in the diagram.
7.5 in.
7.5 in.
3 in.
3 in.
11.5 in.
11.5 in.
What is the total surface area of the rectangular prism in square inches?
A 143.25 in.2
B 241.5 in.?
C 258.75 in
D 286.5 in.?
Answers
Answer:
D.
Step-by-step explanation:
Given: Dimensions of a rectangular prism are \(7.5\,\,inches,3\,\,inches\,,\,11.5\,\,inches\)
To find: total surface area of the rectangular prism in square inches
Solution:
Length of the rectangular prism (l) = 7.5 inches
Breadth of the rectangular prism (b) = 3 inches
Height of the rectangular prism (h) = 11.5 inches
Total surface area of the rectangular prism = 2(lb+bh+hl)
= \(2(7.5\times3+3\times11.5+11.5\times7.5 )\)
\(2(7.5\times3+3\times11.5+11.5\times7.5 )=2(22.5+34.5+86.25)\\=2(143.25)\\=286.5\,\,square \,\,inches\)
So, option D is correct
Answer:
D! I got it correcttt
Step-by-step explanation:
this app is bad its s lie
Answers
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

A tank contains 100 gallons of pure water. At time zero, a sugar-water solution containing 0.2 lb of sugar per gallon enters the tank at a rate of 3 gallons per minute. Simultaneously, a drain is opened at the bottom of the tank allowing the sugar solution to leave the tank at 3 gallons per minute. Assume the solution in the tank is kept perfectly mixed at all times. What will be the eventual sugar content in the tank as time goes to infinity?
Answers
Answer:
20 lbs of sugar per gallon as time goes to infinity
Step-by-step explanation:
Because of the statement ... as time goes to infinity...I am inclined to approach this problem using derivatives and limits
Let the amount of sugar in the tank at any time t(in minutes) be
\(S(t) \;lbs/gal\)
We have \(S(0) = 0\) since the initial quantum of water has zero sugar
The inflow rate of sugar is given as 3 gal/min and each gallon contains 0.2 lbs of sugar
\therefore The rate of sugar increase in the tank n lbs/gal
= 0.2 lbs /gal \times 3 gal/min
= 0.6 lbs/min
Outflow rate = 3 gal/min
At any time t, the tank contains 100 gal
The amount of sugar at time t = \dfrac{S(t)}{100} lbs/gal
Therefore the outflow rate of sugar = 3 gal/min \times \dfrac{S(t)}{100} lbs/gal
= 0.03S(t) lb/min
The net rate is given by inflow rate - outflow rate
= 0.6 - 0.03S(t)
In calculus terms the net rate = \(\dfrac{dS(t)}{dt}\)
Therefore
\(\dfrac{dS(t)}{dt} = 0.6 - 0.03S(t)\)
\(\dfrac{dS(t)}{dt} - 0.03S(t) = 0.6\\\\\) (1)
A trick to solving differential equations of this type is to use the method of integrating factors
In general, if we have a differential equation of the type
\(\dfrac{dy}{dx} + Py = Q\\\\\)
where P and Q are functions only of x
then the integrating factor is \(e^{\int\ {P} \, dx }\)
which you use to multiply both sides of the differential equation first
In equation (1) above,
y = S(t) which well simply write as S for convenience
Writing S' for \(\dfrac{dS(t)}{dt}\) for convenience we get equation (1) as
\(S' + 0.03S =0.6\) (2)
From the above we see that P in the generalized differential equation corresponds to 0.03
Therefore the integrating factor is
\(\mbox {\large e^{\int 0.03dt} = e^{0.03t}}\)
Multiply equation (2) throughout by this integrating factor to get
\(\mbox{\large e^{0.03t} S' + 0.03S e^{0.03t} = 0.6 e^{0.03t} }\)
The left side is nothing but the first derivative of \(\mbox{\large (e^{0.03t}S) }\\\\\)
\(= \mbox{\large (e^{0.03t}S)'\\\\}}\)
Integrating both sides we get
\(\mbox{\large e^{0.03t}S = 0.06 \int e^{0.03t}dt}\\\\\) (3)
\(\textrm{By using the fact that $\int e^{ax} dx = \dfrac{e^{ax}}{a} + C$}:\\\\\mbox{\large \int e^{0.03t}dt} = \dfrac{e^{0.03}}{ 0.03}} + C\\\\\)
Therefore equation (3) becomes
\(e^{0.03t}S = 0.06 \cdot \dfrac{e^{0.03}}{0.03}} + C\\\\e^{0.03t}S = 0.06 \cdot 33.333 \cdot e^{0.03} + C\\\\e^{0.03t}S = 20 \cdot e^{0.03} + C\\\)
Dividing by \(e^{0.03} \textrm{ (same as multiplying by $e^{-0.03}$) both sides}\):
\(S = 20 + Ce^{-0.03t}\\\\\textrm{Plugging back S(t):}\\\\S(t) = 20 + Ce^{-0.03t}\\\)
We are asked to find the level of sugar content as t ⇒ ∞
At t = 0, S(t) = 0; there is no sugar content
S(0) = 0 = 20 + Ce⁰
0 = 20 + C
C = -20
\(S(t) = 20 -20e^{-0.03t}\\\\\)
As t ==> ∞
we get
\(\lim _{x\to \infty }S\left(t\right)=\:\lim _{x\to \infty }\left(20\:-\:20e^{-0.03t}\right)=\:\:20\:-\:0\:=\:20\)
Therefore as time goes to infinity the eventual sugar content
= 20 lbs/gallon
Find the value of x in the triangle shown below.
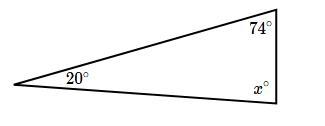
Answers
Answer:
it's so simple
Step-by-step explanation:
20°+74°+x°=180°
x°=180°-94
x°= 86°
Find the area of this triangle

Answers
The calculated area of the triangle is 38.30 square units
How to find the area of the triangleFrom the question, we have the following parameters that can be used in our computation:
The triangle
The area of the triangle is calculated as
Area = 1/2absin(c)
Where
a = b = 10
c = 50 degrees
Using the above as a guide, we have the following:
Area = 1/2 * 10 * 10 * sin(50 degrees)
Evaluate
Area = 38.30
Hence, the area of the triangle is 38.30 square units
Read more about area at
https://brainly.com/question/24487155
#SPJ1
In the xy-plane, what is the y-intercept of the graph of the equation y=6(x-1/2)(x+3)?
Answers
Answer:
The y-intercept of the graph of the equation is -9. This means that the graph crosses the y-axis at the point (0, -9).
Step-by-step explanation:
To solve this question, we need to plug in x = 0 into the given equation and simplify. We get:
y = 6(0 - 1/2)(0 + 3) y = 6(-1/2)(3) y = -9
Therefore, the y-intercept of the graph of the equation is -9. This means that the graph crosses the y-axis at the point (0, -9).
Thao says she can find the answer to 8*90 by halving the 8 and doubling the 90 again and again until she gets down to 1*720 is she correct
Answers
Answer:
yes
Step-by-step explanation:
8 × 90 = 720
4 × 180 (half of 8, double of 90) = 720
2 × 360 (half of 4, double of 180) = 720
1 × 720 = 720
pls anyone mathhhhhhhhhhhh

Answers
Area of rectangle is,
A = 45 units²
And, Perimeter of rectangle is,
⇒ P = 28 units
We have to given that;
Vertices of rectangle are,
⇒ (- 4, - 5)
⇒ (-4, 0)
⇒ (5, 0)
⇒ (5, - 5)
Since, The distance between two points (x₁ , y₁) and (x₂, y₂) is,
⇒ d = √ (x₂ - x₁)² + (y₂ - y₁)²
Hence, Length of rectangle is distance between (- 4, - 5) and (- 4, 0).
Which is,
⇒ d = √ (x₂ - x₁)² + (y₂ - y₁)²
⇒ d = √ (- 4 + 4)² + (0 + 5)²
⇒ d = √ 25
⇒ d = 5
And, Width of rectangle is distance between (- 4, 0) and (5, 0).
Which is,
⇒ d = √ (x₂ - x₁)² + (y₂ - y₁)²
⇒ d = √ (- 4 - 5)² + (0 - 0)²
⇒ d = √ 81
⇒ d = 9
Thus, Area of rectangle is,
A = L x W
A = 5 x 9
A = 45 units²
And, Perimeter of rectangle is,
⇒ P = 2 (L + W)
⇒ P = 2 (5 + 9)
⇒ P = 2 × 14
⇒ P = 28 units
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
x/120 = 1/24 need a step by step answer please

Answers
Answer:
X/120=1/24
5/120=1/24 24×5=120
Step-by-step explanation:
Answer:
Eliminate the denominators of the fractions 120⋅x/200=120⋅2/41
Cancel the multiplied terms that are in the denominator 120
x=120⋅1/4
x=5
The answer is x=5
Angles 1 and 2 form a right angle.Which word describes their measures?
Answers
Answer:
90 degree angle because a right angle is always 90 degrees
Answer:
Step-by-step explanation:
complementary angle- adds to 90°
A bag contains 16 red, 15 blue, and 14 yellow balls. 2 balls are drawn without
replacement. Find the probability that:
a. Blue, then yellow is selected
b. Red, then red is selected
Answers
\(16+15+14=45\) - the total number of balls
\(|\Omega|=45\cdot44=1980\)
a)
\(A\) - blue, then yellow is selected
\(|A|=15\cdot14=210\\\\P(A)=\dfrac{210}{1980}=\dfrac{7}{66}\approx10.6\%\)
b)
A - red, then red is selected
\(|A|=16\cdot15=240\\\\P(A)=\dfrac{240}{1980}=\dfrac{4}{33}\approx12.1\%\)
What’s the answer to this radical functions equation ASAP

Answers
Step-by-step explanation:
√z is defined only when z >= 0
Therefore √x - 1 is defined only when (x - 1) >= 0, x >= 1.
The only graph that shows the domain x >= 1 is graph Y.
sela
Lines a, b, c, and d intersect as shown.
rpod
covery Education
FARI Montage
R
124
95
42
53
39
95
What is x?

Answers
Hope this helps:D