⚠️⚠️please answer⚠️⚠️

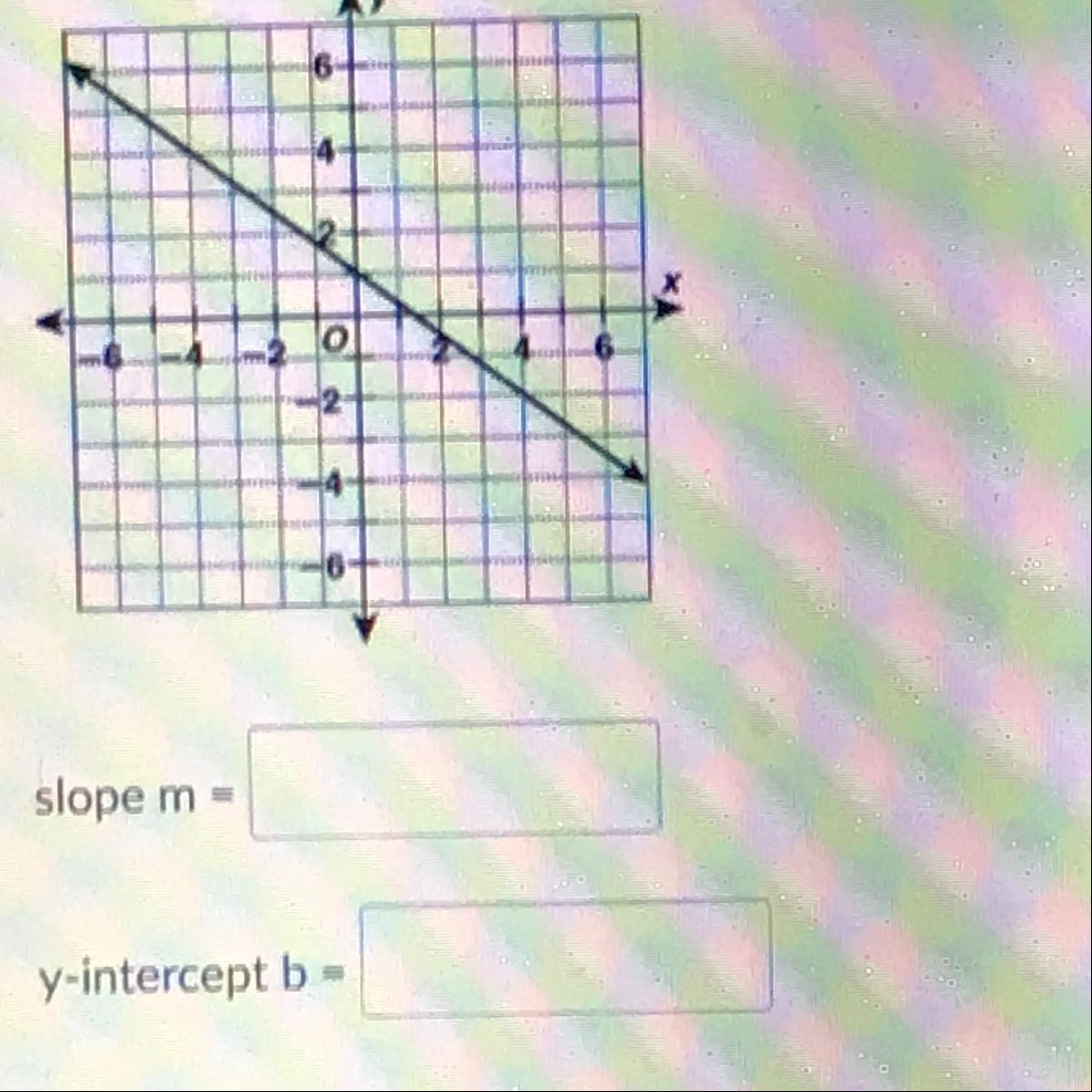
Answer:

2(x + 31.5) = 3x + 24

2x+63= 3x+24

2x+63-63=3x+24-63

x=39

Answer:

\(x=39\)

Step-by-step explanation:

\(2\left(x+31.5\right)=3x+24\)

\(\textbf{Apply the distributive law:-}\)

\(a(b+c)=ab+ac\)

here, a= 2, b=x, c= 31.5

\(2\left(x+31.5\right)\)

\(\textbf{Multiple:-}\) \(2\cdot \:31.5=63\)

\(=2x+63\)

\(2x+63=3x+24\)

\(\textbf{Now, Subtract 63 from both sides:-}\)

\(2x+63-63=3x+24-63\)

\(2x=3x-39\)

\(\textbf{\mathrm{Subtract\:}3x\mathrm{\:from\:both\:sides}:-}\)

\(2x-3x=3x-39-3x\)

\(-x=-39\)

\(\textbf{\mathrm{Divide\:both\:sides\:by\:}-1:-}\)

\(\frac{-x}{-1}=\frac{-39}{-1}\)

\(x=39\)

\(\textbf{OAmalOHopeO}\)

Looking up the z-score of -1.2 in the table, we find that the probability P(x < 81) ≈ 0.1151 (rounded to four decimal places).
So, P(x < 81) = 0.1151.

Given that the random variable x is normally distributed with a mean (µ) of 87 and a standard deviation (σ) of 5, we are asked to find the probability P(x < 81).

To solve this problem, we need to use the standard normal distribution table or a calculator that has the capability to calculate probabilities for a normal distribution.

First, we need to standardize the random variable x by subtracting the mean and dividing by the standard deviation. This process will give us the z-score for x.

z = (x - u) / o

In this case, we have:

z = (81 - 87) / 5 = -1.2

Now, we can use the standard normal distribution table or a calculator to find the probability of getting a z-score less than -1.2.

Using a standard normal distribution table, we find that the probability of getting a z-score less than -1.2 is 0.1151 (rounded to four decimal places).

Therefore, the probability of getting a value of x less than 81 is approximately 0.1151.

P(x<81) = 0.1151 (rounded to four decimal places).

Learn more about probability here:

https://brainly.com/question/11234923

#SPJ11

Answer:

Step-by-step explanation:

sureface area of rectanglur object is the sum of the six sides

     Area = Length x Width

   SArea = Top Area + Bottom Area + Front Area + Back Area + Left Side Area

                 + Right Side Area

        since the top and bottom have equal  area  =  long x wide

                  the front and back have equal  area    = long x tall

                  and both sides have equal area  =  wide x tall

              I summed the bottom front and side areas each times 2

   SArea = 2(Bottom Area) + 2(Front Area) + 2(Side Area)

                 factor out the 2 and added the area formulas for the bottom front

                 and side

              = 2 [ (long x wide) + (long x tall) + (wide x tall)]

              = 2 [ (9 x 4) + (9 x 6) + (4 x 6)]

              = 2 [ (9)(4) + (9)(6) + (4)(6)]

              = 2(    36   +   54   + 24 )

              = 2( 114)

              =   ????    What is 2 times 114  ????       You can finish this part.

Answer: (x,y) ---> (-x,-y)

Step-by-step explanation: When rotating an image 180 degrees, you just need to flip your x and y to negatives. Just remember that 180 degrees is the complete opposite direction, and negative numbers are the opposite of positive numbers.

Hope this helps!

Answer:

it's answer is definitely 8

Step-by-step explanation:

-4 (x-2) + 6x

or, -4x + 8 + 6x

or, 2x + 8

so definitely answer is 8

the gamma distribution becomes approximately normal due to the Central Limit Theorem when n is large.X ︽.Norm(a/λ, a/λ²) since it is an approximately normal distribution with mean a/λ and variance a/λ².

(a) Gamma random variables are sums of random variables, and as n gets large, the Central Limit Theorem applies. When n is large, the gamma random variable with parameters (n, λ) approaches a normal distribution, as the sum of independent and identically distributed Exponential(λ) random variables is distributed roughly as a normal distribution with mean n/λ and variance n/λ². In other words, the gamma distribution becomes approximately normal due to the Central Limit Theorem when n is large.

(b) The problem asks to show that:lim (1 + x/n)-n = e⁻x.The expression (1 + x/n)⁻ⁿ can be written as [(1 + x/n)¹/n]ⁿ. Now letting n → ∞ in this equation and replacing x with aλ yields the desired result from part (a):lim (1 + x/n)ⁿ

= lim [(1 + aλ/n)¹/n]ⁿ

= e⁻aλ(d)

The central limit theorem with continuity correction can be expressed as:P(Z ≤ z) ≈ Φ(z + 0.5/n)if X ~ B(n,p), where Φ is the standard normal distribution and Z is the standard normal variable.

This continuity correction adjusts for the error made by approximating a discrete distribution with a continuous one.(e) The exact probability that the walk is within 500 steps from the origin can be calculated by using the normal distribution. Specifically, we have that:

P(|X - a/λ| < 500)

= P(-500 < X - a/λ < 500)

= P(-500 + a/λ < X < 500 + a/λ)

= Φ((500 + a/λ - μ)/(σ/√n)) - Φ((-500 + a/λ - μ)/(σ/√n)),

where X ~ N(μ, σ²), and in this case, μ = a/λ and σ² = a/λ².

Therefore, X ︽.Norm(a/λ, a/λ²) since it is an approximately normal distribution with mean a/λ and variance a/λ².

To know more about gamma distribution Visit:

https://brainly.com/question/28077799

#SPJ11

I say it's 10$ because surprise is on the side and quality is on the bottom surprised the line is hitting 10 which it will be $10

A stochastic process X(t) is called a martingale if the expected value of X(t) given all information available up to and including time s is equal to the value of X(s).

Thus, to show that the process X(t):=e^(t/2)cos(W(t)), 0 ≤ t ≤ T is a martingale w.r.t. any filtration for Brownian motion, we need to prove that E(X(t)|F_s) = X(s), where F_s is the sigma-algebra of all events up to time s.

As X(t) is of the form e^(t/2)cos(W(t)), we can use Itô's lemma to obtain the differential form:dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt

Taking the expectation on both sides of this equation gives:E(dX) = E(e^(t/2)cos(W(t))dW) - 1/2 E(e^(t/2)sin(W(t))dt)Now, as E(dW) = 0 and E(dW^2) = dt, the first term of the right-hand side vanishes.

For the second term, we can use the fact that sin(W(t)) is independent of F_s and therefore can be taken outside the conditional expectation:

E(dX) = - 1/2 E(e^(t/2)sin(W(t)))dt = 0Since dX is zero-mean, it follows that X(t) is a martingale w.r.t. any filtration for Brownian motion.

Now, let's represent X(t) as an Itô process on the interval [0,T]. Applying Itô's lemma to X(t) gives:

dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt= dM + 1/2 e^(t/2)sin(W(t))dt

where M is a martingale with M(0) = 0.

Thus, X(t) can be represented as an Itô process on [0,T] of the form:

X(t) = M(t) + ∫₀ᵗ 1/2 e^(s/2)sin(W(s))ds

Hence, we have shown that X(t) is a martingale w.r.t. any filtration for Brownian motion and represented it as an Itô process on any time interval [0,T], T > 0.

To know more about martingale visit:
brainly.com/question/32735198

#SPJ11

Factor by grouping: 16x³ +28x² - 28x - 49 = 0 is  (4x² - 7) (4x - 7) = 0

Large polynomials can be divided into groups based on a common factor. As a result, we may factor each distinct group and then merge like words. We refer to this as factoring by grouping.

We have the equation,

16x³ +28x² - 28x - 49 = 0

In order to solve the equation by using factor by grouping:

We find common terms in between,

So, we arrange the terms,

16x³ +28x² - 28x - 49 = 0

4x² (4x - 7) -7 (4x - 7) = 0

Here, we have common term (4x-7).

Factor out the common binomial.

(4x² - 7) (4x - 7) = 0

Therefore, (4x² - 7) (4x - 7) = 0 is the factor.

To learn more about the factoring by grouping;

https://brainly.com/question/11919488

#SPJ1

Step-by-step explanation: To evaluate functions substitute the given number or expression function's variable.

Answer:

heeeeeeereeeeeeee

Step-by-step explanation:

The other four angles will be 7∏/3, 13∏/3, 19∏/3, and 31∏/3

Generally, given cos (x), the value that is similar to cos x will be sum of the angle and multiple of 360.

Hence for the angle cos(∏/3), the angles similar to this angle will be expressed as:

Cos(2∏n + ∏/3) where:

The other four angles will be 7∏/3, 13∏/3, 19∏/3, and 31∏/3

Learn more on trigonometry identity here: https://brainly.com/question/7331447

Answer:

4.75+0.75

Step-by-step explanation:

The equation that help find length of scarf is l = 0.75 + 4.75

The result of adding two or more numbers is called a sum.

Given,

           Length of striped scarf = 0.75 feet

           Length of remaining scarf = 4.75 feet

Total length = Length of striped scarf + Length of remaining scarf

 Hence,           l    =   0.75  +   4.75

To learn more about addition visit:

https://brainly.com/question/29464370

#SPJ1

Answer:

4/5

Step-by-step explanation:

Answer:

Step-by-step explanation:

here you go mate

step 1

-10+7m= -10  equation

step 2

7m-10+10=-10+10

7m=0

step 3

\(\frac{7m}{7} =\frac{0}{7}\)  divide

answer

m=0

mind if i get brainliest?

Answer:Isolate the variable by dividing each side by factors that don't contain the variable.

M=0

Step-by-step explanation:

A professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6.

First, let's define some variables to represent the probabilities of making a hole for a professional golfer and an amateur golfer:

Let p be the probability that a professional golfer makes a hole with the new club.

Let q be the probability that an amateur golfer makes a hole with the new club.

According to the company's claims, we know that:

p = 1.2q (since the professional golfer makes a hole 120% of the time, which is 1.2 times the probability of the amateur golfer making a hole)

Next, we need to determine the probability of each golfer making a hole during one round of golf, which consists of 18 holes. Let's assume that each hole is independent of the others, meaning that the outcome of one hole does not affect the outcome of another. In that case, the probability of making at least one hole in a round can be calculated using the complement rule:

The probability that a professional golfer makes at least one hole in a round is 1 minus the probability that the golfer misses every hole: \(1 - (1-p)^{18} .\)

The probability that an amateur golfer makes at least one hole in a round is\(1 - (1-q)^{18} .\)

Now, let's use these probabilities to calculate the expected number of holes each golfer will make in 5 rounds of golf:

The expected number of holes made by a professional golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-p)^{18} )\times18.\)

The expected number of holes made by an amateur golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-q)^{18} )\times18.\)

We can simplify these expressions using the relationship between p and q:

The expected number of holes made by a professional golfer in 5 rounds is \(518(1 - (1-1.2q)^{18} ).\)

The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ).\)

We can now evaluate these expressions using the values of p and q:

\(p = 1.2q, so q = p/1.2\)

Substituting this into the expressions above, we get:

The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2(p/1.2))^{18} ) = 518(1 - (1-p)^{18} ).\)

The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-p/1.2)^{18} ).\)

Finally, we can evaluate these expressions using the given probabilities:

The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2q)^{18} ) = 518(1 - (1-1.2(0.1))^{18} ) = 40.7.\)

The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ) = 518(1 - (1-0.1/1.2)^{18} ) = 1.6.\)

So according to these calculations, we would expect a professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6

for such more question on probability

https://brainly.com/question/24756209

#SPJ4

Answer:

2 orders

Step-by-step explanation:

Step one:

given data

The local store sells at $24 per pair of jeans

Cost = $24

The online store sells at $22 per pair plus a shipping fee of $6 per order

let the number of orders be x

Cost= 22+6x

For 1 order

the online store will cost

Cost= 22+6*1

Cost= 22+6

Cost= $28

For 2 orders

The local shop cost

Cost= 24*2= $48

The online store will cost

Cost= 22+6*2

the online store will cost

Cost= 22+12

Cost= $34

Hence Tim should place at least 2 orders if he wants to buy online

Answer:

# of orders is 2 ORDERS!!!

Step-by-step explanation:

I hope this helps!!!

The area of the kite is 40 square meters, calculated by using the area of a kite formula.

To calculate the area of a kite, you need to know the lengths of both the diagonals. Once you have those values, you can use the following formula to find the area:

Area = (d1 x d2) / 2

where d1 and d2 are the lengths of the diagonals.

Here is an example of how to use this formula:

Let's say you have a kite with diagonals of 8 meters and 10 meters. To find the area, you would use the formula:

Area = (8 x 10) / 2

Area = 40 square meters

So the area of the kite is 40 square meters.

There are also many online calculators available that can help you find the area of a kite if you enter the values of the diagonals.

To learn more about kite please click on below link        

https://brainly.com/question/15640807

#SPJ4

Hey there!

48:

1, 2, 3, 4, 6, 8, 12, 16, 24, & 48

132:

1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, & 132

LIKE TERMS:

1, 2, 3, 4, 6, & 12

HIGHEST NUMBER:

12

Therefore, your answer is: 12 (Option D.)

Good luck on your assignment & enjoy your day!

~Amphitrite1040:)

If a cone is sliced by a vertical plane that passes through the vertex, the resulting cross section will be a triangle.

The vertical plane cuts through the cone at its highest point, which is also the point where the two sides of the cone meet (i.e. the vertex). As the plane cuts through the cone, it intersects with the sloping sides of the cone at different angles, creating a triangular shape.

The resulting cross section will have the same base as the original cone, which is a circle. However, the height of the cross section will be shorter than the height of the original cone, since the vertical plane has removed a portion of the cone.

Overall, the resulting cross section will be a triangle with a circular base, which is often referred to as a frustum. This shape is commonly used in architecture and engineering, as it allows for tapered structures such as pillars and columns to be created.

Learn more about cross section here: https://brainly.com/question/16881438

#SPJ11

Answer:

r=8

Step-by-step explanation:

SORRY IF IM LATE <3

-1/2R-1=3-r

-R-2 =6-2R

-R+R-2=6

-R+R-2=6+2

r=6+2

r=8

Answer:

81

Step-by-step explanation:

you evaluate by mutiplying the number with the exponent, which is -9 multiplied by -9, which is 81 because 2 negatives multipled or divided is a positive. hope this helped a bit

Answer:

81

Step-by-step explanation:

Here, some steps to evaluate (-9)².

Step 1 :- A negative base raised to an even powers equal positive.

Step 2 :- Write exponentiation as multiplicaton.

Step 3 :- Multiply it .

Another way to evaluate ( -9 ) ².

Evaluate by multiply with it's exponent.

When two negative sign combine they formed positive

So, after multiplying we get 81.

Answer:

65, 140, 40

Step-by-step explanation:

1. ∠ZXY is on the circle, m∠ZXY = 130/2 = 65°

Do 3) first

3) ∠SVY is inside the circle, so

m∠SVY = 1/2 * (arc SY + arc XR) = 1/2 * (40 + 40) = 40°

2) m∠XVS = 180° - m∠XVS = 180 - 40 = 140°

Answer: 72cm³

Step-by-step explanation:

The picture here is a cuboid. The volume of a cuboid is calculated using the formula:

= Length × Width × Height

= 6cm × 3cm × 4cm

= 72cm³

Therefore, the volume is 72cm³

Answer:

1)I don't know

2)-2

Step-by-step explanation:

2)6-5(1/1/x)= 2

6-5(1/1)-x= 2

6-6-x=2

-x/-1=2/-1

x= -2

Answer:

Step-by-step explanation: