Answers
Answer:
9
Step-by-step explanation:
\(05 \times 2. \div 2\)
Related Questions
professional tennis player serena williams has a career win record of 81%. if we took a simple random sample of 60 of her matches, what is the probability that at least 50 would be wins?
Answers
The statement that justifies the shape of the sampling distribution being approximately normal is np > 10 and n(1 - P) > 10. The correct answer is D).
In this case, "n" represents the sample size, and "p" represents the probability of success (winning a match in this context).
For a binomial distribution, the sample proportion follows an approximately normal distribution when both np and n(1 - P) are greater than 10.
In the given scenario, if we assume that the sample size is 60 and the probability of winning a match is 0.81 (81%), we can check if np and n(1 - P) are both greater than 10
np = 60 * 0.81 = 48.6
n(1 - P) = 60 * (1 - 0.81) = 11.4
Since both np > 10 and n(1 - P) > 10 are satisfied (48.6 > 10 and 11.4 > 10), we can conclude that the shape of the sampling distribution of the sample proportion is approximately normal. The correct option is D).
To know more about sampling distribution:
https://brainly.com/question/31465269
#SPJ4
--The given question is incomplete, the complete question is given below " Professional tennis player Serena Williams has a career win record of 81%. If we took a simple random sample of 60 of her matches, what is the probability that at least 50 would be wins? A USE SALT The shape of the sampling distribution of the sample proportion is approximately normal. Which of the following choices justifies that statement? a, The sample size is greater than 30. b, We have sampled less than 10% of the population. c, A random sample was taken. d, np > 10 and n(1-P)>10 "
Natalie is making costumes each costume has 4 buttons that costs 3 cents and a zipper costs 7 cents how much does she spend on buttons and a zipper for each costume?
Answers
Answer:
19 cents
Step-by-step explanation:
Natalie buys 4 buttons at 3 cents each. She also buys 1 zipper at 7 cents
We are to find the total amount that she spends for each costume
I converted cents to dollars.
4 buttons at 3 cents = 4x0.03 (3 cents is 0.03 dollars)
= 0.12
The zipper = 7 cents = 0.07 dollars
The total amount she spent = 0.12+ 0.07
= 0.19 dollars = 19 cents
Therefore she 19 cents in total for each costume
4 buttons at
help me and ill give brainlist!!!!!

Answers
Hope this helps!
Mark me brainliest ^^
plss..I need help...

Answers
The estimate on an explanatory variable is not statistically significant at the 5%-level if the t-statistic is greater than 2.5. the p-value is less than 0.05. the 95% confidence interval does not contain zero. the 95% confidence interval contains zero.
Answers
The estimated value of the explanatory variable is not statistically significant at the 5%-level if a. the t-statistic is greater than 2.5.
The t-test is a hypothesis testing technique used to decide whether the estimated coefficient of a linear regression model is statistically significant or not. The t-value is used to measure the size of the difference between the estimated coefficient and the hypothesized value. When the t-value exceeds a critical value, such as 2.5, the estimated value of the explanatory variable is not significant at the 5%-level. It implies that the null hypothesis, which assumes that the explanatory variable's coefficient is zero, cannot be rejected.
The p-value is a measure of the probability of obtaining a more extreme value of the test statistic than the observed value if the null hypothesis is true. A small p-value implies that the null hypothesis should be rejected. When the p-value is less than 0.05, it means that the estimated value of the explanatory variable is significant at the 5%-level.
The confidence interval is a range of values that is expected to include the true value of the population parameter with a specified level of confidence. A 95% confidence interval means that the true value of the population parameter lies within the range 95% of the time. The 95% confidence interval does not contain zero implies that the estimated value of the explanatory variable is statistically significant at the 5%-level since it suggests that the population parameter is different from zero at the 5%-level. Conversely, if the 95% confidence interval contains zero, the estimated value of the explanatory variable is not statistically significant at the 5%-level since it means that the population parameter is not different from zero at the 5%-level. Therefore, it is essential to examine the t-statistic, p-value, and confidence interval while conducting hypothesis testing to make an informed decision.
To leran more about hypothesis testing, refer:-
https://brainly.com/question/17099835
#SPJ11
assume that 20% of criminal suspects who agree to take lie detector tests are actually guilty while 80% of those who agree to take the test are innocent. of those who are guilty, 70% fail the lie detector test. of those who are innocent, only 15% fail the test. suppose a person is arrested and takes a lie detector test. given that the person fails the test, what is the probability that the person is actually innocent?
Answers
The probability that the person is actually innocent given that they have failed the test is 0.4615... or approximately 0.462.
The question asks us to calculate the probability that the person is actually innocent given that they have failed the test. The probability that the person is actually innocent is given by the formula: P(innocent | fails test) = P(innocent and fails test) / P(fails test).
Now we need to calculate the values of the probabilities on the right-hand side of this equation. P(fails test) is equal to the sum of the probabilities that a guilty person fails the test and that an innocent person fails the test. Hence, P(fails test) = P(guilty and fails test) + P(innocent and fails test). P(guilty and fails test) = 0.2 × 0.7 = 0.14P(innocent and fails test) = 0.8 × 0.15 = 0.12. Therefore, P(fails test) = 0.14 + 0.12 = 0.26.
Finally, we can calculate the probability that the person is actually innocent given that they have failed the test: P(innocent | fails test) = P(innocent and fails test) / P(fails test)= 0.12 / 0.26= 0.4615 (rounded to four decimal places).
Therefore, the probability that the person is actually innocent given that they have failed the test is 0.4615... or approximately 0.462.
To know more about probability refer here:
https://brainly.com/question/11234923
#SPJ11
I need help with this ASAP, I’ll give brainliest if correct

Answers
Within-groups design compares which of the following same subjects across time two or more groups with different subjects two or more independent groups across time none of the above
Answers
Within-groups design compares the same subjects across time. In this design, participants are measured or observed on multiple occasions, such as before and after an intervention or at different time points.
The purpose of the within-groups design is to examine changes within individuals over time, allowing researchers to assess the impact of an intervention or the natural progression of a phenomenon within the same group of subjects.
By comparing the same subjects across time, within-groups designs help to control for individual differences and increase the internal validity of the study.
This design allows researchers to evaluate the effectiveness of an intervention by assessing changes within individuals and determining if those changes are statistically significant.
It also allows for a more precise assessment of the impact of an intervention or the stability of a phenomenon over time.
Within-groups designs are commonly used in fields such as psychology, education, and medicine to study changes in behavior, cognition, or health outcomes.
They provide valuable insights into individual responses to interventions or the natural course of development or disease progression within a specific group of subjects.
To know more about intervention refer here:
https://brainly.com/question/28235244#
#SPJ11
If x · y = z, which of the following statements is true?
zy=x
z - y = x
z - x = y
xz=y
Answers
Answer:
b
Step-by-step explanation:
Which r-value represents the weakest correlation
a.-0.75 ,
b. -0.27,
c. 0.11,
d. 0.54
Answers
The weakest correlation is represented by the value of c. 0.11.
The weakest correlation is represented by the value that is closest to zero, as it indicates a weaker relationship between the variables. In this case, the answer is: c. 0.11
A correlation coefficient of 0.11 is closer to zero than the other options provided, indicating a weaker correlation compared to the rest. The negative values (-0.75 and -0.27) represent negative correlations, but their magnitudes are larger than 0.11, making them stronger correlations (although still considered weak in general). The positive value of 0.54 represents a moderate positive correlation.
To know more about correlation, refer here:
https://brainly.com/question/30116167
#SPJ4
\(\sf 8x+10=3x+20\)
Answers
5x = 10
x = 10/5
x = 2
the answer is 2
hope that helps! :)
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The value of x is ~
\( \boxed{2}\)\( \large \boxed{ \mathfrak{Step\:\: By\:\:Step\:\:Explanation}}\)
\(8x + 10 = 3x + 20\)\(8x - 3x = 20 - 10\)\(5x = 10\)\(x = 10 \div 5\)\(x = 2\)Write – 0.425 as a fraction in simplest form.
Answers
Hi there!
This should be easy,lol!
Answer:
\(\boxed{-\frac{17}{40} }\)
Step-by-step explanation:
Rewrite the decimal number as a fraction with 1 in the denominator.
Then
Multiply to remove 3 decimal places. Here, you multiply top and bottom by 103 = 1000
And then....
Find the Greatest Common Factor (GCF) of 425 and 1000, if it exists, and reduce the fraction by dividing both numerator and denominator by GCF = 25.
Therefore x = -17/40
In conclusion, – 0.425 = -17/40
Have a great day/night!
Write and solve an equation to find the value of x
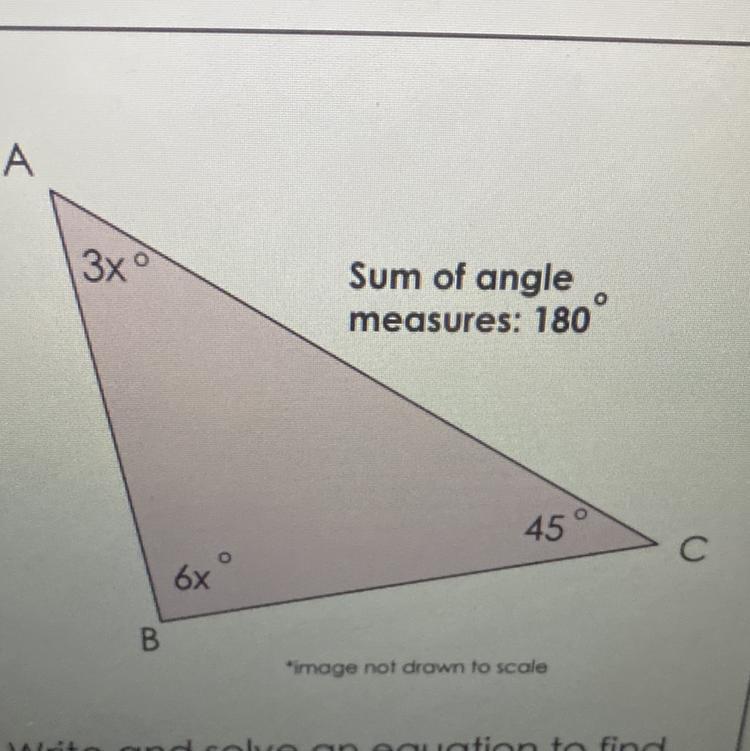
Answers
Answer:
3x=45°
6x=90°
Step-by-step explanation:
As the sum of angle measures is 180° , to find the x
First, you create an equation that looks like,
\(180 = 45+3x+6x\)
which can be written as
\(180=45+9x\)
since both 3x and 6x have the same variable. Then you subtract 45 from both sides of the equation
\(180-45=9x\)
(+45 on the right side can be cancelled by -45, so there is none left)
\(135=9x\)
Now, you can divide both sides by 9
\(\frac{135}{9} = x\)
So you must have an answer of x = 15°
Similar to ratios, 3:6 each part is 15°, now you have to multiply 3 to 15 and 6 to 15 to see how they separate the angles of 135°.
3×15= 45
6×15=90
To check them add 45, 90 and 45 to see if it adds up to 180. The answer is at the top and if my explanation is wrong please tell me, Thanks
What is the measure of circumscribed
O 45°
O 50°
O 90°
O 95°

Answers
The measure of the inscribed angle is equal to 90 degrees
What is an inscribed angleThe inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle.
In this problem, the side length of the square is 5 which forms 90 degrees to all the other sides.
The measure of the circumscribed angle is 90 degree
Learn more on inscribed angle here;
https://brainly.com/question/3538263
#SPJ1
Calculate the double integral. 6x/(1 + xy) dA, R = [0, 6] x [0, 1]
Answers
The value of the double integral ∬R (6x/(1 + xy)) dA over the region
R = [0, 6] × [0, 1] is 6 ln(7).
To calculate the double integral ∬R (6x/(1 + xy)) dA over the region
R = [0, 6] × [0, 1], we can integrate with respect to x and y using the limits of the region.
The integral can be written as:
∬R (6x/(1 + xy)) dA = \(\int\limits^1_0\int\limits^6_0\) (6x/(1 + xy)) dx dy
Let's start by integrating with respect to x:
\(\int\limits^6_0\)(6x/(1 + xy)) dx
To evaluate this integral, we can use a substitution.
Let u = 1 + xy,
du/dx = y.
When x = 0,
u = 1 + 0y = 1.
When x = 6,
u = 1 + 6y
= 1 + 6
= 7.
Using this substitution, the integral becomes:
\(\int\limits^7_1\) (6x/(1 + xy)) dx = \(\int\limits^7_1\)(6/u) du
Integrating, we have:
= 6 ln|7| - 6 ln|1|
= 6 ln(7)
Now, we can integrate with respect to y:
= \(\int\limits^1_0\) (6 ln(7)) dy
= 6 ln(7) - 0
= 6 ln(7)
Therefore, the value of the double integral ∬R (6x/(1 + xy)) dA over the region R = [0, 6] × [0, 1] is 6 ln(7).
Learn more about double integral here:
brainly.com/question/15072988
#SPJ4
The value of the double integral \(\int\limits^1_0\int\limits^6_0 \frac{6x}{(1 + xy)} dA\), over the given region [0, 6] x [0, 1] is (343/3)ln(7).
Now, for the double integral \(\int\limits^1_0\int\limits^6_0 \frac{6x}{(1 + xy)} dA\), use the standard method of integration.
First, find the antiderivative of the function 6x/(1 + xy) with respect to x.
By integrating with respect to x, we get:
∫(6x/(1 + xy)) dx = 3ln(1 + xy) + C₁
where C₁ is the constant of integration.
Now, we apply the definite integral over x, considering the limits of integration [0, 6]:
\(\int\limits^6_0 (3 ln (1 + xy) + C_{1} ) dx\)
To proceed further, substitute the limits of integration into the equation:
[3ln(1 + 6y) + C₁] - [3ln(1 + 0y) + C₁]
Since ln(1 + 0y) is equal to ln(1), which is 0, simplify the expression to:
3ln(1 + 6y) + C₁
Now, integrate this expression with respect to y, considering the limits of integration [0, 1]:
\(\int\limits^1_0 (3 ln (1 + 6y) + C_{1} ) dy\)
To integrate the function, we use the property of logarithms:
\(\int\limits^1_0 ( ln (1 + 6y))^3 + C_{1} ) dy\)
Applying the power rule of integration, this becomes:
[(1/3)(1 + 6y)³ln(1 + 6y) + C₂] evaluated from 0 to 1,
where C₂ is the constant of integration.
Now, we substitute the limits of integration into the equation:
(1/3)(1 + 6(1))³ln(1 + 6(1)) + C₂ - (1/3)(1 + 6(0))³ln(1 + 6(0)) - C₂
Simplifying further:
(343/3)ln(7) + C₂ - C₂
(343/3)ln(7)
So, the value of the double integral \(\int\limits^1_0\int\limits^6_0 \frac{6x}{(1 + xy)} dA\), over the given region [0, 6] x [0, 1] is (343/3)ln(7).
To learn more about integration visit :
brainly.com/question/18125359
#SPJ4
This trapezoid has been divided into two right triangles and a rectangle.
How can the area of the trapezoid be determined using the area of each shape?
Enter your answers in the boxes.
The area of the rectangle is in², the area of the triangle on the left is in², and the area of the triangle on the right is in².
The area of the trapezoid is the sum of these areas, which is in².
Trapezoid ABCD with parallel sides DC and AB. Points F and E are between D and C. FEBA form a rectangle with 4 right angles. D F is 2 inches, F E is 14 inches, E C is 2 inches, A B is 14 inches., and E B is 12 inches.
Answers
Answer:
here it is
Step-by-step explanation:
This trapezoid has been divided into two right triangles and a rectangle.
How can the area of the trapezoid be determined using the area of each shape?
Enter your answers in the boxes.
The area of the rectangle is in², the area of the triangle on the left is in², and the area of the triangle on the right is in².
The area of the trapezoid is the sum of these areas, which is in².
Trapezoid ABCD with parallel sides DC and AB. Points F and E are between D and C. FEBA form a rectangle with 4 right angles. D F is 2 inches, F E is 14 inches, E C is 2 inches, A B is 14 inches., and E B is 12 inches.
The factory quality control department discovers that the conditional probability of making a manufacturing mistake in its precision ball bearing production is 4 % 4\% 4% on Tuesday, 4 % 4\% 4% on Wednesday, 4 % 4\% 4% on Thursday, 8 % 8\% 8% on Monday, and 12 % 12\% 12% on Friday. The Company manufactures an equal amount of ball bearings ( 20 % 20\% 20%) on each weekday. What is the probability that a defective ball bearing was manufactured on a Friday?
Answers
Answer:
The probability that a defective ball bearing was manufactured on a Friday is 0.375.
Step-by-step explanation:
The conditional probability of an events X given that another event A has already occurred is:
\(P(X|A)=\frac{P(A|X)P(X)}{P(A)}\)
The information provided is as follows:
P (D|M) = 0.08
P (D|Tu) = 0.04
P (D|W) = 0.04
P (D|Th) = 0.04
P (D|F) = 0.12
It is provided that the Company manufactures an equal amount of ball bearings, 20% on each weekday, i.e.
P (M) = P (Tu) = P (W) = P (Th) = P (F) = 0.20
Compute the probability of manufacturing a defective ball bearing on any given day as follows:
\(P(D)=P(D|M)P(M)+P(D|Tu)P(Tu)+P(D|W)P(W)\\+P(D|Th)P(Th)+P(D|F)P(F)\)
\(=(0.08\times 0.20)+(0.04\times 0.20)+(0.04\times 0.20)+(0.04\times 0.20)+(0.12\times 0.20)\\\\=0.064\)
Compute the probability that a defective ball bearing was manufactured on a Friday as follows:
\(P(F|D)=\frac{(D|F)P(F)}{P(D)}\)
\(=\frac{0.12\times 0.20}{0.064}\\\\=0.375\)
Thus, the probability that a defective ball bearing was manufactured on a Friday is 0.375.
An automatic filling machine is used to fill 2-litre bottles of cola. The machine’s output is known to be approximately Normal with a mean of 2.0 litres and a standard deviation of 0.01 litres. Output is monitored using means of samples of 5 observations.
Determine the upper and lower control limits that will include roughly 95.5 percent of the sample means.
If the means for 6 samples are 2.005, 2.001, 1.998, 2.002, 1.995 and 1.999, is the process in control?
Answers
The upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
To determine the upper and lower control limits for the sample means, we can use the formula:
Upper Control Limit (UCL) = Mean + (Z * Standard Deviation / sqrt(n))
Lower Control Limit (LCL) = Mean - (Z * Standard Deviation / sqrt(n))
In this case, we want to include roughly 95.5 percent of the sample means, which corresponds to a two-sided confidence level of 0.955. To find the appropriate Z-value for this confidence level, we can refer to the standard normal distribution table or use a calculator.
For a two-sided confidence level of 0.955, the Z-value is approximately 1.96.
Given:
Mean = 2.0 litres
Standard Deviation = 0.01 litres
Sample size (n) = 5
Using the formula, we can calculate the upper and lower control limits:
UCL = 2.0 + (1.96 * 0.01 / sqrt(5))
LCL = 2.0 - (1.96 * 0.01 / sqrt(5))
Calculating the values:
UCL ≈ 2.0018 litres
LCL ≈ 1.9982 litres
Therefore, the upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
Mean of the sample means = (2.005 + 2.001 + 1.998 + 2.002 + 1.995 + 1.999) / 6 ≈ 1.9997
Since the mean of the sample means falls within the control limits (between UCL and LCL), we can conclude that the process is in control.
Learn more about means from
https://brainly.com/question/1136789
#SPJ11
Absolute value graphing pls help on all preferably step by step

Answers
The graph of the absolute value functions is added as an attachment
Graphing the absolute value functionsAn absolute value function is represented as
y = a|x - h| + k
Where the vertex is
Vertex = (h, k)
Using the above as a guide, we have the following:
The vertex of y = |x| - 1 is (0, -1)The vertex of y = |x + 1| + 4 is (-1, 4)The vertex of y = 2|x| - 2 is (0, -2)The vertex of y = 3|x - 4| + 1 is (4, -1)The vertex of y = -2|x - 2| is (2, 0)The vertex of y = -2|x - 2| - 1 is (2, -1)Next, we plot the graph of the functions using the vertex
See attachment for the graph of the absolute value functions where color is used to represent the key/legend
Read more about absolute value function at
https://brainly.com/question/10538556
#SPJ1

Consider the function h(x) = x3 – 2x. Find the value of h(3).=AnswerE KeyKeyboard Shoh(3) =-

Answers
To find h(3) we need to substitute x = 3 into h(x) as follows:
\(\begin{gathered} h(x)=x^3-2x \\ h(3)=3^3-2(3) \\ h(3)=27-6 \\ h(3)=21 \end{gathered}\)
Carlos graphed the system of equations that can be used to solve x cubed minus 2 x squared 5 x minus 6 = negative 4 x squared 14 x 12. On a coordinate plane, 2 functions are shown. The functions intersect at (negative 3, negative 66), (negative 2, negative 32), and (3, 18) What are the roots of the polynomial equation? –3, –2, 3 –3, 2 18, 32 18, 32, 66
Answers
Answer: A
Step-by-step explanation: the other guy is wrong
latrell's pool table is 3 feet wide and 7 feet long. latrell wants to replace the felt on the pool table. the felt costs $5.00 per square foot. how much would it cost in total to replace the felt on the pool table?
Answers
Latrell would need to pay 105 to replace the felt on his pool table.
Latrell has a pool table that is 3 feet wide and 7 feet long.
The pool table's felt needs to be replaced, and the cost of the felt per square foot is $5.00.
Let's find out how much it would cost Latrell to replace the pool table's felt.
What is the surface area of the pool table.
To determine the surface area of the pool table,
we need to multiply the length by the width, as shown below:
Surface area = length × width
Surface area = 7 ft × 3 ft
Surface area = 21 square feet
Now that we know the surface area of the pool table, we can determine the cost of the felt.
Latrell will need 21 square feet of felt, and it costs $5.00 per square foot.
We can use the following formula to determine the total cost of the felt:
Total cost of felt = cost per square foot × surface area.
Total cost of felt = $5.00 × 21 square feet.
Total cost of felt = $105
For similar question on surface area of rectangle
https://brainly.com/question/30337697
#SPJ11
Three of the vertices of a parallelogram are A(2, 4), B(6,2) and C (8, 6).(a) Plot the point A, B and C in the coordinate plane(b) Find the mid-point of diagonal AC(c) Find the fourth vertex D(d) Find the length of diagonal AC(e) Find the perimeter of ABCD.
Answers
Given:
Three of the vertices of a parallelogram are given as
\(\begin{gathered} A\left(2,4\right)_ \\ B\left(6,2\right) \\ C(8,6) \end{gathered}\)Required:
(a) Plot the point A, B and C in the coordinate plane
(b) Find the mid-point of diagonal AC
(c) Find the fourth vertex D
(d) Find the length of diagonal AC
(e) Find the perimeter of ABCD.
Explanation:
Take D coordinate as (x,y)
now midpoint of AC and BD is same so
\(\begin{gathered} (\frac{2+8}{2},\frac{4+6}{2})=(\frac{x+6}{2},\frac{2+y}{2}) \\ \\ (5,5)=(\frac{x+6}{2},\frac{2+y}{2}) \\ \\ x=4,y=8 \end{gathered}\)midpoint of AC
\((\frac{2+8}{2},\frac{4+6}{2})=(5,5)\)length of diagonal AC
\(AC=\sqrt{36+4}=2\sqrt{10}\)perimeter of ABCD
\(AB=\sqrt{16+4}=\sqrt{20}\)\(BC=\sqrt{4+16}=\sqrt{20}\)perimeter is
\(2(AB+BC)=4\sqrt{20}\)Final answer:
(b) Find the mid-point of diagonal AC
\(\begin{equation*} (5,5) \end{equation*}\)(c) Find the fourth vertex D
\((4,8)\)(d) Find the length of diagonal AC
\(2\sqrt{10}\)(e) Find the perimeter of ABCD.
\(\begin{equation*} 4\sqrt{20} \end{equation*}\)
an investor has $25,000 that he can invest today. in addition to this amount, he can also invest $12,500 per year for 30 years (beginning one year from now) at which time he will retire. he plans on living for 25 years after he retires. if interest rates are 7.5 percent, what size annual annuity payment can he obtain for his retirement years? (all annuity payments are at year-end. round your answer to the nearest dollar.)
Answers
The investor can obtain an annual annuity payment of approximately $48,651 for his retirement years.
To calculate the annual annuity payment, we can use the present value of an ordinary annuity formula. The formula is:
PV = C × [(1 - (1 + r)^-n) / r]
Where:
PV is the present value of the annuity,
C is the annual payment,
r is the interest rate,
n is the number of periods.
In this case, the investor has a retirement period of 25 years, and the interest rate is 7.5%.
The present value of the annuity is the amount the investor can invest today plus the present value of the annual payments he can make for 30 years.
Using the formula, we can solve for C, the annual payment, which comes out to approximately $48,651.
Visit here to learn more about annuity:
brainly.com/question/14908942
#SPJ11
how many distinguishable orderings of the letters of millimicron contain the letters cr next to each other in order and also the letters on next to each other in order?
Answers
There are 1,663,200 different orderings of the letters of millimicron containing the letters cr next to each other in order and the letters next to each other in order.
Total no. of letters = 11
Millimicron, dissecting will give us the following:
Number of m = 2
Number of i = 3
Number of l = 2
Number of c = 1
Number of n =1
Number of r = 1
Number of o = 1
o compute this by using permutation
total no. of ways to arrange = 11! ÷ [ 2! × 3! × 2! × 1! × 1! × 1! × 1!]
= 39,916,800 ÷ 24
= 1,663,200 is the answer
Learn more about permutation and combination at
https://brainly.com/question/14298835?referrer=searchResults
#SPJ4
find the slope of the tangent line to the polar curve at r = sin(4theta).
Answers
The slope of the tangent line to the polar curve at
`r = sin(4θ)` is:
`dy/dx = (dy/dθ)/(dx/dθ)`
at `r = sin(4θ)`= `(4cos(4θ)sin(θ) + sin(4θ)cos(θ)) / (4cos(4θ)cos(θ) - sin(4θ)sin(θ))`
To find the slope of the tangent line to the polar curve at
`r = sin(4θ)`,
we can use the polar differentiation formula, which is:
`dy/dx = (dy/dθ)/(dx/dθ)`
For a polar curve given by
`r = f(θ)`,
we can find
`(dy/dθ)` and `(dx/dθ)`
using the following formulas:
`(dy/dθ) = f'(θ)sin(θ) + f(θ)cos(θ)` and `(dx/dθ) = f'(θ)cos(θ) - f(θ)sin(θ)`
where `f'(θ)` represents the derivative of `f(θ)` with respect to `θ`.
For the given curve,
`r = sin(4θ)`,
we have
`f(θ) = sin(4θ)`.
So, we first need to find `f'(θ)` as follows:
`f'(θ) = d/dθ(sin(4θ)) = 4cos(4θ)`
Now, we can substitute
`f(θ)` and `f'(θ)` in the above formulas to get
`(dy/dθ)` and `(dx/dθ)`
:
`(dy/dθ) = f'(θ)sin(θ) + f(θ)cos(θ)`` = 4cos(4θ)sin(θ) + sin(4θ)cos(θ)`
and
`(dx/dθ) = f'(θ)cos(θ) - f(θ)sin(θ)`` = 4cos(4θ)cos(θ) - sin(4θ)sin(θ)
Now, we can find the slope of the tangent line using the polar differentiation formula:
`dy/dx = (dy/dθ)/(dx/dθ)`
at
`r = sin(4θ)`
So, the slope of the tangent line to the polar curve at
`r = sin(4θ)` is:
`dy/dx = (dy/dθ)/(dx/dθ)`
at `r = sin(4θ)`= `(4cos(4θ)sin(θ) + sin(4θ)cos(θ)) / (4cos(4θ)cos(θ) - sin(4θ)sin(θ))`
To know more about slope visit:
https://brainly.com/question/3605446
#SPJ11
Suppose Appendix Table A.3 contained Φ(z) only for z ≥0 Explain how you could still computea. P( –1.72≤ Z ≤–.55)b. P( –1.72≤ Z ≤ .55)Is it necessary to tabulate Φ(z) for z negative? What property of the standard normal curve justifies your answer?
Answers
It is not necessary to tabulate Φ(z) for negative z-values since we can always use the symmetry property to find the corresponding area for positive z-values. This property holds because the standard normal curve is symmetric around its mean of 0.
a. To compute P(-1.72 ≤ Z ≤ -0.55) when Appendix Table A.3 only contains Φ(z) for z ≥ 0, you can use the property of symmetry of the standard normal curve. Since the curve is symmetric around z = 0, Φ(-z) = 1 - Φ(z). So, you can find the values for positive z and use the symmetry property:
P(-1.72 ≤ Z ≤ -0.55) = Φ(-0.55) - Φ(-1.72) = (1 - Φ(0.55)) - (1 - Φ(1.72)) = Φ(1.72) - Φ(0.55)
b. To compute P(-1.72 ≤ Z ≤ 0.55), you can break it into two parts: P(-1.72 ≤ Z ≤ 0) and P(0 ≤ Z ≤ 0.55). Then, use the symmetry property for the negative part:
P(-1.72 ≤ Z ≤ 0.55) = P(-1.72 ≤ Z ≤ 0) + P(0 ≤ Z ≤ 0.55) = Φ(0) - Φ(-1.72) + Φ(0.55) - Φ(0) = Φ(1.72) + Φ(0.55)
It is not necessary to tabulate Φ(z) for z negative because the standard normal curve is symmetric around z = 0, and we can use the property Φ(-z) = 1 - Φ(z) to find probabilities for negative z values. This property allows us to calculate probabilities for negative z values without needing a separate table for them.
If Appendix Table A.3 only contained Φ(z) for z ≥0, we could still compute P( –1.72≤ Z ≤–.55) and P( –1.72≤ Z ≤ .55) by using the symmetry property of the standard normal curve. This property states that the area under the curve to the left of a negative z-score is the same as the area to the right of the corresponding positive z-score.
To apply this property, we would first find the z-scores for the given ranges by using the formula z = (x – μ)/σ, where μ and σ are the mean and standard deviation of the standard normal distribution, respectively. For P( –1.72≤ Z ≤–.55), the negative z-scores would correspond to positive x-values, so we would need to use the symmetry property to find the corresponding area for positive z-scores. Specifically, we would find P( .55 ≤ Z ≤ 1.72) using the table, and then subtract this from 1 to get P( –1.72≤ Z ≤–.55).
Similarly, for P( –1.72≤ Z ≤ .55), the negative z-score would correspond to negative x-values, so we would use the symmetry property to find the area for positive z-scores from 0 to .55, and then double this to account for the area to the left of 0.
It is not necessary to tabulate Φ(z) for negative z-values since we can always use the symmetry property to find the corresponding area for positive z-values. This property holds because the standard normal curve is symmetric around its mean of 0, meaning that the area to the left of any negative z-score is the same as the area to the right of the corresponding positive z-score.
Learn more about probabilities here: brainly.com/question/30034780
#SPJ11
What is the approximate distance from the origin to the point (−5, 6, −1)? Round to the nearest tenth.
o3.2 units
o3.5 units
o7.7 units
o7.9 units
Answers
Answer:the answer is o.7.7
Step-by-step explanation:
bruh someone help me

Answers
Answer:
Think about it this way: The x axis goes from left to right, correct? So just try to visualize actually picking up the object and flipping it over that axis. So since one tip of the triangle is on the coordinate (1,1), after reflecting the shape that same tip would be on (1,-1). You understand?
You won $48 in a ping-pong tournament. You Figure that you will pend an average of $3. 00 of your winning each day
Answers
Answer:
You will be able to spend your money for a total of 16 days.
Step-by-step explanation:
Total money won: $48
Since you are starting off with $48, divide the amount of money you will be using each day. 48 divided by 3 is equal to 16.
