Please give me the correct answer.
Answers
Answer:
What is the question?
Step-by-step explanation:
Related Questions
Marlene estimates that 48% of 1,220 is about 600. Which estimates describes why this is a reasonable estimate?
Answers
Answer:
By rounding
Step-by-step explanation:
48 % means 48 percent which 48 out of 100.
48% of 1220
= 48/100*1220
= 0.48*1220
=585.6 which is almost equal to 600
1) By rounding
Now if we round 48% we get 50 % as 8 > 5 and 1 is added to 4 making it 5 in tens place leaving 0 in unit's place.
So 50% of 1220
0.50*1220= 610
Again rounding 610 would give 600 as 1 is less than 5 and we drop it out from the tens place leaving zero behind.
2) Complementary
IF we subtract 48% from 100% we get 52%.
So 52% of 1220 would be 634.4
IT again can be rounded in 2 ways Either 52% can be rounded to 50% and 634.4 can be rounded to 600.
Both would give 600
linearity. a function f : r n → r is linear if for any x and y in the domain of f, and any scalar α and β, f(αx + βy) = αf(x) + βf(y). are the following functions linear? justify your answer
Answers
The two expressions are not equal, so the function f(x) = 2x² is also not linear.
To determine if a function is linear, we need to verify if it satisfies the linearity property, which states that for any x and y in the domain of the function and any scalars α and β, the function should satisfy f(αx + βy) = αf(x) + βf(y).
Let's examine each function and determine if it is linear:
f(x) = 3x - 2
To check linearity, we need to verify if f(αx + βy) = αf(x) + βf(y). Let's substitute the values:
f(αx + βy) = 3(αx + βy) - 2
= 3αx + 3βy - 2
On the other hand:
αf(x) + βf(y) = α(3x - 2) + β(3y - 2)
= 3αx - 2α + 3βy - 2β
Comparing the two expressions, we can see that they are not equal, so the function f(x) = 3x - 2 is not linear.
f(x) = 2x²
Using the same logic, let's check linearity:
f(αx + βy) = 2(αx + βy)²
= 2(α²x² + 2αβxy + β²y²)
= 2α²x² + 4αβxy + 2β²y²
On the other hand:
αf(x) + βf(y) = α(2x²) + β(2y²)
= 2αx² + 2βy²
The two expressions are not equal, so the function f(x) = 2x² is also not linear.
In conclusion, neither of the given functions is linear since they do not satisfy the linearity property.
Learn more about linear here:
https://brainly.com/question/31510530
#SPJ11
NEED GENIUS HELP!!!
Select the function that's represented in the graph.
Question options:
A)
ƒ(x) = –(x + 2)² – 3
B)
ƒ(x) = (x + 2)² – 3
C)
ƒ(x) = –(x – 2)² – 3
D)
ƒ(x) = (x – 2)² – 3
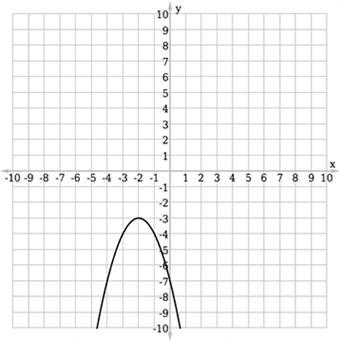
Answers
Answer: A
Step-by-step explanation:
If you look at option A and ignore the -(x+2)^2, it would say f(x) = -3.
So the vertex has y-coordinate -3.
Because the coefficient of -(x+2)^2 is negative, the graph opens downward.
Because it says -(x+2)^2 instead of -(x-2)^2, it will be on the left side of the graph.
The graph meets all of these conditions.
The graph described in option B opens upwards.
The graph described in option C opens upwards and the vertex is in the fourth quadrant.
The graph described in option D opens downwards, but the vertex is in the fourth quadrant.
Suppose a certain baseball diamond is a square 60 feet on a side. The pitching rubber is located 40.5 feet from home plate on a line joining home plate and second
base.
(a) How far is it from the pitching rubber to first base?
(b) How far is it from the pitching rubber to second base?
(c) If a pitcher faces home plate, through what angle does he need to turn to face first base?
(a) The distance from the pitching rubber to first base is about feet.
(Round to two decimal places as needed.)
(b) The distance from the pitching rubber to second base is about feet.
(Round to two decimal places as needed.)
(c) He needs to turn about to his left.
(Round to one decimal place as needed.)
Answers
Answer: 41.7 feet from pitcher to 1st
13.2 feet from pitcher to 2nd
58 degrees to turn from home to 1st
distance from pitcher to the line from home to 1st is 57.5(sin45) = 57.5(.707) = 40.66
construct a right triangle with legs 40.66 and 50-40.66 = 9.34. then sum the legs' squares, and take the square root to get 41.72 feet
distance from home to 2nd = hypotenuse of a right triangle with sides 50 and 50, and angle of 45 degrees
50^2 + 50^2 = 2(2500) = 5000. sqr5000= 70.71, subtract 57.5. 70.71-57.5= 13.21 feet from pitcher to 2nd
Step-by-step explanation:
Let u, v, w be vectors in R³. Which of the following statements are True? If u wand vw, then (u + v) i w u.vxw=ux v.w If u l vand vw, then u w D (u×v) L (u+v) 1 pts Consider the set S of all 5-tuples of positive real numbers, with usual addition and scalar multiplication. Which of the following vector space properties are NOT satisfied? Ou+vis in S whenever u, v are in S. For every u in S, there is a negative object-u in S, such that u +-u=0 u+v=v+u for any u, v in S. ku is in S for any scalar k and any u in S. There is a zero object 0 in S, such that u + 0 = u
Answers
All the vector space properties mentioned in the given options are satisfied in the set S of all 5-tuples of positive real numbers are true.
In the given statements:
If u and v are vectors and u ∧ v, then (u + v) ∥ u ∧ v.
u · (v ∧ w) = (u · v) ∧ w.
If u ∥ v and v ∧ w, then u ∥ (v ∧ w).
(u × v) · (u + v) = 0.
The true statements among these are:
If u and v are vectors and u ∧ v, then (u + v) ∥ u ∧ v.
u · (v ∧ w) = (u · v) ∧ w.
To determine the true statements among the given options, let's analyze each option individually:
Option 1: Ou + vis in S whenever u, v are in S.
This statement is true because in the set S of all 5-tuples of positive real numbers, the sum of two positive real numbers is always positive.
Option 2: For every u in S, there is a negative object -u in S, such that u + (-u) = 0.
This statement is true because in the set S, for any positive real number u, the negative of u (-u) is also a positive real number, and the sum of u and -u is zero.
Option 3: u + v = v + u for any u, v in S.
This statement is true because addition of 5-tuples in S follows the commutative property, where the order of addition does not affect the result.
Option 4: ku is in S for any scalar k and any u in S.
This statement is true because when multiplying a positive real number (u in S) by any scalar k, the result is still a positive real number, which belongs to S.
Option 5: There is a zero object 0 in S, such that u + 0 = u.
This statement is true because the zero object 0 in S is the 5-tuple consisting of all zeros, and adding 0 to any element u in S leaves u unchanged.
To learn more about positive real numbers click here:
brainly.com/question/30278283
#SPJ11
An independent basic service set (IBSS) consists of how many access points?
Answers
An independent basic service set (IBSS) does not consist of any access points.
In an IBSS, devices such as laptops or smartphones connect with each other on a peer-to-peer basis, forming a temporary network. This type of network can be useful in situations where there is no existing infrastructure or when devices need to communicate with each other directly.
Since an IBSS does not involve any access points, it is not limited by the number of access points. Instead, the number of devices that can be part of an IBSS depends on the capabilities of the devices themselves and the network protocols being used.
To summarize, an IBSS does not consist of any access points. Instead, it is a network configuration where wireless devices communicate directly with each other. The number of devices that can be part of an IBSS depends on the capabilities of the devices and the network protocols being used.
Know more about access points here,
https://brainly.com/question/11103493
#SPJ11
HELPP PLSSSSSSSSSS i would really appreciate it

Answers
Applying exponential properties, we have that the solution to the given expression is:
\(-\frac{125}{343}\)
How do we proceed when a fraction is elevated to the exponent?When a fraction is elevated to the exponent, we apply the exponent to both the numerator and the denominator.
In this problem, we have that:
The numerator is of 5, hence 5³ = 125.The denominator is of 7, hence 7³ = 343.Negative base with odd exponent, hence the solution is negative and given as follows:
\(-\frac{125}{343}\)
More can be learned about exponential properties at https://brainly.com/question/25263760
#SPJ1
H(-9,3) and A (8,-3)Find the midpoints?
Answers
The given points are
\(\begin{gathered} H(-9,3) \\ A(8,-3) \end{gathered}\)We are asked to find the midpoint.
Recall that the midpoint formula is given by
\((x,y)=\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\)We have
\(\begin{gathered} x_1=-9 \\ x_2=8 \\ y_1=3 \\ y_2=-3 \end{gathered}\)Substitute the given values into the midpoint formula.
\(\begin{gathered} (x,y)=\frac{-9+8}{2},\frac{3-3}{2} \\ (x,y)=\frac{-1}{2},\frac{0}{2} \\ (x,y)=(-\frac{1}{2},0) \end{gathered}\)Therefore, the midpoint of H(-9, 3) and A (8, -3) is found to be
\((x,y)=(-\frac{1}{2},0)\)Or it can also be written in the decimal notation as
\((x,y)=(-0.5,0)\)James and Kian both took an online IQ exam independently. The probability that James will pass the test is 0.8 and Kian is 0.7 respectively.Find the probabilities that neither one of them will pass the test.
Answers
Answer:
they both will fail because, it says that james has a 0.1 more chance of passing the test compared to Kian but it no where states the amount to pass the test nor that they both will pass
For a normal distribution, find the X-value when the Z-value equals 2.15 and the mean is 36 and the standard deviation is 16. 1.24 70.4 0.98 32.1
Answers
The correct X-value when the Z-value equals 2.15, with a mean of 36 and a standard deviation of 16, is 70.4.
To find the X-value corresponding to a given Z-value in a normal distribution, you can use the formula:
X = Z * σ + μ
Where X is the X-value, Z is the Z-value, σ is the standard deviation, and μ is the mean.
In this case, the Z-value is 2.15, the mean is 36, and the standard deviation is 16. Plugging these values into the formula, we get:
X = 2.15 * 16 + 36 = 70.4
Therefore, the X-value when the Z-value equals 2.15, with a mean of 36 and a standard deviation of 16, is 70.4.
Learn more about statistics here:
https://brainly.com/question/30915447
#SPJ11
What is the height of a cylinder with a volume of 384x cubic inches and a radius of 8 inches? Round to the nearest tenth of an inch. inches
Answers
Answer: what's the x after 384?
Step-by-step explanation:
PLSSS HELP IF YOU TRULY KNOW THISSS

Answers
Answer: 1/50
Step-by-step explanation:
Step 1: We need to multiply the numerator and denominator by 100 since there are 2 digits after the decimal.
0.02 = (0.02 × 100) / 100
= 2 / 100 [ since 0.02 × 100 = 2 ]
Step 2: Reduce the obtained fraction to the lowest term
Since 2 is the common factor of 2 and 100 so we divide both the numerator and denominator by 2.
2/100 = (2 ÷ 2) / (100 ÷ 2) = 1/50
HELP PLSSSSS ASAPPPPP WILL REWARD BRAINLIEST
3) Find the value of x. A) 9B) 10C) 11D) 12

Answers
Answer:
i thinkis D 11 because 8+3=11
Answer:
the answer is D
Step-by-step explanation:
hope this helps
With explanation please! ASAP

Answers

What is the solution for Vx+12 =x?
Show all your work.
Answers

Answer: x = 12/1-v
1. Subtract Vx from both sides.
12 = x - Vx
2. Factor out the common term x.
12 = x(1 - v)
3. Divide both sides by 1 - v.
12/1 - v = x
4. Switch sides.
X = 12/1 - v
help! as soon as possible

Answers
The quadrilateral is a type of "kite", as the pair of adjacent angles are equal.
Explain about the features of kite:A quadrilateral known as a kite has four sides that may be grouped into two adjacent pairs of equal-length sides, and the diagonals cross each other at right angles. The quadrilateral is a polygon with four sides.
Kite's two diagonals meet at a right angle to form its properties.A kite's primary diagonal is symmetrical.The diagonal's primary opposed angles are equal.A set of congruent triangles having a common base can be thought of as the kite.The kite is split into two isosceles triangles by the shorter diagonal.Thus, the quadrilateral is a type of "kite", as the pair of adjacent angles are equal.
Know more about the kite
https://brainly.com/question/30763486
#SPJ1
In order to investigate treatments for morbid obesity, obese subjects satisfying fairly strict requirements were randomly assigned to one of three groups: gastric bypass surgery; participation in a diet and exercise program; or both gastric bypass surgery and participation in the diet and exercise program. Researchers carefully observed the amount of weight lost five years after the study began. Reference: Ref 9-1 This study uses the principles of A. randomization. B. confounding. C. blocking. D. All of the above Which of the following are principles of experimental design?
A. randomization B. replication C. blinding D. All of the above
Answers
Since all three principles of experimental design are likely to have been used in the study described, Therefore option D is correct.
All of the above are principles of experimental design. Randomization helps to ensure that groups are similar in all aspects except for the treatment received, reducing the effects of confounding variables. Replication allows for assessing the variability and consistency of results. Blinding reduces the risk of bias by preventing participants or researchers from knowing which treatment was received. The study described in the question uses all of these principles of experimental design.
To know more about experimental design, visit the link given below:
https://brainly.com/question/29337791
#SPJ4
You can infer causality from a correlational result, but only when the r value is greater than ?A. 0B. 5C. 1
Answers
You can infer causality from a correlational result, but only when the r value is greater than:
C. 1
Causality refers to a situation in which one event causes another. When there is a correlation between two variables, it means that they tend to move in the same direction.
However, this does not necessarily mean that one event causes the other. In order for a correlation to indicate causality, the correlation coefficient (r) must be greater than 1. If the correlation coefficient is below 1, then there is not enough evidence to suggest that one event causes the other.
In addition, there are other factors that need to be considered when assessing causality from a correlational result.
For example, the strength of the relationship between the variables, the direction of the relationship, and the consistency of the results over time. It is also important to consider the context in which the research was conducted, as this may have an effect on the results.
Learn more about causality:
brainly.com/question/9369134
#SPJ4
Josie is planning for her graduation party and uses the function J(p) = 200 + 25p, where J(p) represents the total cost of the party and p is the number of people attending. To help budget for her graduation party, she wants to be able to determine the total cost for varying amounts of people who could attend. Which of the following graphs could Josie use to help her budget?
Answers
option C, which shows a line graph, is the appropriate graph that Josie can use to help her budget.
What is the linear function?
A linear function is defined as a function that has either one or two variables without exponents. It is a function that graphs to a straight line.
Josie can use a line graph to help her budget since the given function is a linear function.
The graph of a linear function is a straight line, and a line graph is a graph that represents data with points connected by straight lines.
Therefore, option C, which shows a line graph, is the appropriate graph that Josie can use to help her budget.
To learn more about the linear function visit:
brainly.com/question/29612131
#SPJ1
Complete question:
The graphs are in the attached image.

solve the following LP problem and find the optimal feasible solution. does the solution is LP special case? if yes what type of special case is it? you can either write the solution and scan your answer or type using word.doc Max 2x1 + 6x2 s.t. 2 x1 + 5 x1 <4 x1 + 2 x2 < 14 4 x1 + x2 < 6 x1 > 0, x2 > 0
Answers
The optimal feasible solution is x1 = 1, x2 = 0.4, and the problem is a regular linear programming problem.
The optimal feasible solution is x1 = 1 and x2 = 0.4, and the problem is a regular linear programming problem without any special case conditions?To solve the given linear programming problem, let's define the decision variables and formulate the objective function and constraints:
Decision Variables:
x1, x2
Objective Function:
Maximize: 2x1 + 6x2
Constraints:
2x1 + 5x2 ≤ 4
4x1 + x2 ≤ 6
x1, x2 > 0
To find the optimal feasible solution, we can use a linear programming solver. Here is the optimal solution for the given problem:
Optimal Solution:
x1 = 1
x2 = 0.4
The maximum value of the objective function is obtained when x1 = 1 and x2 = 0.4. The maximum value is 2(1) + 6(0.4) = 4.8.
Now let's analyze if the solution is a special case of linear programming.
This problem falls under the category of Linear Programming (LP) problems. However, it does not represent any specific special case of LP such as degeneracy, unboundedness, or infeasibility. The given problem has a feasible solution, and the objective function is maximized within the given constraints. Hence, it is a regular LP problem without any special case conditions.
Note: Since the solution is text-based, there is no need to scan or provide a separate file.
Learn more about optimal feasible solution
brainly.com/question/29450014
#SPJ11
Sam is ordering shirts online. The shipping is a flat rate of $5.99, and each shirts costs $12.50. He spent $80.99 in total. How many shirts did he order
Answers
Based on the shipping rate and the price of the t-shirts, it can be concluded Sam ordered a total of 6 t-shirts.
What equation represents Sam's situation?5.99 + x12.50 = 80.99
x represents the number of t-shirts she bough, which is the focus of the equation.
Let's solve it:
5.99 + x12.50 = 80.99x12.50 = 80.99 - 5.99x12.50 = 75x = 75 / 12.50x = 6How many t-shirts did Sam order?Sam ordered 6 t-shirts.
Learn more about equations in: https://brainly.com/question/10413253
Find the volume and surface area of the figure below.

Answers
The volume of the prism is determined as 1,416 m³ and the surface area of the prism is 664.8 m².
Volume of the prismThe volume of the prism is determined from the product of base area and slant height of the prism.
Base of the prism, A = ¹/₂bh = ¹/₂ x 12 x 20 = 120 m²
Volume = AL
where;
L is the slant heightL² = (12/2)² + (20.3/2)²
L² = 6² + 10.15²
L² = 139.0225
L = 11.8 m
V = AL
V = 120 x 11.8 = 1,416 m³
Surface area of the prismA = bh + pL
A = (12 x 20) + 11.8(12 + 12 + 12)
A = 664.8 m²
Learn more about volume of prism here: https://brainly.com/question/23963432
#SPJ1
Find g(x), where g(x) is the translation 1 unit left of f(x)= –7x+10
Answers
The translation 1 unit left of f ( x ) =–7x+10 then g(x) is -7x + 3.
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction either in its range(involving values of y) or in its domain(involving values of x).
The up and down movements are in the vertical direction by the y coordinate.
The left and right movements are in the horizontal direction by the x coordinate.
When translating a graph, adding units moves the graph to the left, and eliminating units moves the graph to the right.
hence we say that;
f(x) = –7x+10
g(x) = f(x + 1)
= –7(x + 1)+10
= -7x - 7 + 10
= -7x + 3
Learn more on translation:
brainly.com/question/1046778
#SPJ1
Find the center and radius of the circle x2 + y2 –6y – 16 = 0
Answers
Answer:
centre=(0,3) radius =5
Step-by-step explanation:
Find the median and mean of the following data set:
14, 16, 48, 22, 50, 39
Answers
Median = 30.5
Mean = 31.5
========================================================
Explanation:
The first task is to sort the items from smallest to largest.
{14, 16, 48, 22, 50, 39} sorts to {14, 16, 22, 39, 48, 50}
The median is the middle-most value. Since we have an even number of items here, the middle-most position is a tie between slots 3 and 4
The values in those slots are 22 and 39 respectively. The midpoint of them is (22+39)/2 = 30.5 which is the median
-----------------
To get the mean, we add up the values
14+16+22+39+48+50 = 189
Then we divide by 6 since there are 6 numbers here
189/6 = 31.5 is the mean
vince ships boxes of lasagna in insulated containers. vince has 400 boxes of lasagna to ship. each insulated container can hold 15 boxes of lasagna. each insulated container costs $9.35 to ship regardless of the number of boxes of lasagna in it. he wants to use the least number of insulated containers as possible. how much will it cost vince to ship the boxes of lasagna?
Answers
A building supply company sells sand by the cubic foot and by the cubic yard. The price of one cubic year of sand is $33. 75. What do you think the price of one cubic foot of sand should be? Explain answer
Answers
The price of one cubic yard of sand is $33.75, then the price of one cubic foot of sand should be $1.25.
To determine the price of one cubic foot of sand, we need to convert cubic yards to cubic feet. One cubic yard is equal to 27 cubic feet (3 feet x 3 feet x 3 feet). Therefore, if the price of one cubic yard of sand is $33.75, then the price of one cubic foot of sand should be $33.75/27 = $1.25.
This makes sense because one cubic yard contains 27 cubic feet. So, if the price of one cubic yard is $33.75, then the price per cubic foot should be 1/27th of that price.
It is important to note that this assumes the price per unit of sand remains constant regardless of the quantity purchased. In reality, bulk purchases may result in a discounted price per unit. Additionally, factors such as transportation costs and demand may also affect the price of sand.
To know more about price refer here:
https://brainly.com/question/1315492#
#SPJ11
find the volume of the solid enclosed by the paraboloids z = 4 \left( x^{2} y^{2} \right) and z = 8 - 4 \left( x^{2} y^{2} \right).
Answers
We are given that two paraboloids are given by the following equations:z = 4(x^2y^2)z = 8 - 4(x^2y^2)We need to find the volume of the solid enclosed by these two paraboloids.
Let's first graph the paraboloids to see how they look. The graph is shown below:Volume enclosed by the two paraboloidsThe solid that we need to find the volume of is the solid enclosed by the two paraboloids. To find the volume, we need to find the limits of integration. Let's integrate with respect to x first. The limits of x are from -1 to 1. To find the limits of y, we need to solve the two equations for y. For the equation z = 4(x^2y^2), we get y = sqrt(z/(4x^2)). For the equation z = 8 - 4(x^2y^2), we get y = sqrt((8-z)/(4x^2)). Thus the limits of y are from 0 to the minimum of these two equations, which is given by y = min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2))).We are now ready to find the volume. The integral that we need to evaluate is given by:∫(∫(4(x^2y^2) - (8 - 4(x^2y^2)))dy)dx∫(∫(4x^2y^2 + 4(x^2y^2) - 8)dy)dx∫(∫(8x^2y^2 - 8)dy)dxThe limits of y are from 0 to min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2))). The limits of x are from -1 to 1. Thus we get:∫(-1)1∫0min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2)))(8x^2y^2 - 8)dydxAnswer more than 100 words:Using the above equation, we can evaluate the integral by making a substitution y = sqrt(z/(4x^2)). Thus, we get dy = sqrt(1/(4x^2)) dz. We can then replace y and dy in the integral to get:∫(-1)1∫04(x^2)(z/(4x^2))(8x^2z/(4x^2) - 8)sqrt(1/(4x^2))dzdx∫(-1)1∫04z(2z - 2)sqrt(1/(4x^2))dzdx∫(-1)1∫04z^2 - zsqr(1/(x^2))dzdx∫(-1)1∫04z^2 zsqr(1/(x^2))dzdx∫(-1)1(16/3)x^2dx∫(-1)11(16/3)dx(16/3)∫(-1)1x^2dxThe last integral can be easily evaluated to give:∫(-1)1x^2dx = (1/3)(1^3 - (-1)^3) = (2/3)Thus, we get the volume of the solid enclosed by the two paraboloids as follows:Volume = (16/3) x (2/3) = 32/9Thus, the volume of the solid enclosed by the two paraboloids is 32/9. Therefore, the main answer is 32/9.
The volume of the solid enclosed by the two paraboloids z = 4(x²y²) and z = 8 - 4(x²y²) is 32/9 cubic units. We used the limits of integration and integrated with respect to x and y.
To learn more about Integration click:
brainly.com/question/31744185
#SPJ11
The volume of the solid enclosed by the paraboloids \(z = 4 (x^2y^2)\) and \(z = 8 - 4 (x^2y^2)\) can be found using the triple integral. The triple integral is given as: \(\int\int\int\) dV where the limits of the integrals depend on the bounds of the solid. The bounds can be found by equating the two paraboloids and solving for the values of x, y and z.
The two paraboloids intersect at \(z = 4 (x^2y^2) = 8 - 4 (x^2y^2)\) which simplifies to \((x^2y^2) = 1/2\). Thus, the bounds of the solid are:\(0 \leq z \leq 4 (x^2y^2)0 \leq z \leq 8 - 4 (x^2y^2)0 \leq x^2y^2 \leq 1/2\) the bounds for x and y are symmetric and we can integrate the solid using cylindrical coordinates.
Thus, the integral becomes:\(\int\int\int\) r dz r dr dθwhere r is the distance from the origin and θ is the angle from the positive x-axis. Substituting the bounds, we get:\(\int0^2\ \pi \int0\sqrt(1/2) \int4 (r^2\cos^2\ \theta\sin^2\theta) r\ dz\ dr\ d\ \theta + \int0^2\ \pi \int \sprt(1/2)^1 \int8 - 4 (r^2cos^2\thetasin^2\theta)\)solving this integral, we get the volume of the solid.
he volume of the solid enclosed by the paraboloids \(z = 4 (x^2y^2)\) and \(z = 8 - 4 (x^2y^2)\) is given as: \(8\pi /3\)
To know more about volume visit -
brainly.com/question/30681924
#SPJ11
Use the graph to determine the following.
a. the function's domain
b. the function's range
c. the x-intercepts, if any
d. the y-intercept, if any
e. the function values, f(1) and f(4).
Assume that the graph of the function
continues its trend beyond the displayed coordinate grid.

Answers
R: (-2, negative infinity)
X - Intercepts: Non-existent
Y - Intercepts: (0,-4)
f(1)=-3
f(4)=-4
From the graph of function,
a. Domain = (-∞, ∞)
b. Range = [-2, -∞)
c. x-intercept = NA
d. y-intercept = (0, -4)
e. f(1) = -3 and f(4) = -4
What is domain of a function?"It is a set of points which for which the function is well defined."
What is the range of the function?"It is the set of all possible output values."
What is intercept?"It is a point at which the graph of the function intersects the x-axis or y-axis."
For given example,
From the graph of a function we can observe that, function takes all values of x
So, domain = (-∞, ∞)
The value of the function starts from -2 and it tends towards -∞.
So, Range of f(x) = [-2, -∞)
From the graph of a function we can observe that the graph of a function does not intersect the x-axis.
So, for given function has no x-intercept.
The graph of the function intersects y-axis at (0, -4).
So, y-intercept = (0,-4)
We need to find the value of f(1) and f(4)
From the graph,
for x = 1,
⇒ f(1) = -3
for x = 4,
⇒ f(4) = -4
Therefore, from the graph of function,
a. Domain = (-∞, ∞)
b. Range = [-2, -∞)
c. x-intercept = NA
d. y-intercept = (0, -4)
e. f(1) = -3 and f(4) = -4
Learn more about the domain, range, intercepts here:
https://brainly.com/question/24123211
#SPJ2
how to determine if a function is even or odd algebraically
Answers
You can "find algebraically" if a function is even, odd, or neither by taking it, substituting -x for x, simplifying it, and then comparing the results to what you had initially.
The function is even if it is exactly the same as what you started with (that is, if f(-x) = f (x), with all the signs remaining the same. The function is odd if it is exactly the opposite of what you started with (that is, if f(-x) = -f(x), with all the signs switched.
The function is neither even nor odd if the outcome is neither exactly the same nor exactly the opposite (that is, neither having all the same words but with all the signs reversed).
To learn more about odd and even algebraic function link is here
brainly.com/question/24336402
#SPJ4