Answers
Answer:
at least three sides it can have more if you look up polygons it will tell you that polygons have three sides or more of their shapes
Step-by-step explanation:
Related Questions
What is the domain of the given function?

Answers
domain is {x | x, -6, -1, 0, 3}
To determine the domain of the given function, we need to identify all the valid input values (x-values) for which the function is defined. Looking at the given data, we have the following pairs of x and y values: (-6, -7), (-1, 1), (0, 9), and (3, -2).
The domain of the function is simply the set of all x-values from these pairs. Thus, the domain of the function is {-6, -1, 0, 3}, as these are the valid input values for which we have corresponding output values.
In summary, the domain of the given function is {-6, -1, 0, 3}.
Therefore, domain is {x | x, -6, -1, 0, 3}
Learn more about domain here
https://brainly.com/question/30133157
#SPJ2
Enrique has a recipe for fruit punch that uses 12 cups of pineapple juice. He wants triple the recipe for a family party. How many quarts of pineapple juice died Enrique need for the party?
A. 9
B.10
C.36
D.4
Answers
Answer:
A. 9 quarts
Step-by-step explanation:
Since he wants to triple the recipe you would multiply the 12 cups by 3 to get 36 cups and then you would convert the cups into quarts and 36 cups is equal to 9 quarts
Consider the function f(x,y)=2x2−4x+y2−2xy subject to the constraints x+y≥1xy≤3x,y≥0 (a) Write down the Kuhn-Tucker conditions for the minimal value of f. (b) Show that the minimal point does not have x=0.
Answers
The minimal point does not have x = 0.
(a) Kuhn-Tucker conditions for the minimal value of fThe Kuhn-Tucker conditions are a set of necessary conditions for a point x* to be a minimum of a constrained optimization problem subject to inequality constraints. These conditions provide a way to find the optimal values of x1, x2, ..., xn that maximize or minimize a function f subject to a set of constraints. Let's first write down the Lagrangian: L(x, y, λ1, λ2, λ3) = f(x, y) - λ1(x+y-1) - λ2(xy-3) - λ3x - λ4y Where λ1, λ2, λ3, and λ4 are the Kuhn-Tucker multipliers associated with the constraints. Taking partial derivatives of L with respect to x, y, λ1, λ2, λ3, and λ4 and setting them equal to 0, we get the following set of equations: 4x - 2y - λ1 - λ2y - λ3 = 0 2y - 2x - λ1 - λ2x - λ4 = 0 x + y - 1 ≤ 0 xy - 3 ≤ 0 λ1 ≥ 0 λ2 ≥ 0 λ3 ≥ 0 λ4 ≥ 0 λ1(x + y - 1) = 0 λ2(xy - 3) = 0 From the complementary slackness condition, λ1(x + y - 1) = 0 and λ2(xy - 3) = 0. This implies that either λ1 = 0 or x + y - 1 = 0, and either λ2 = 0 or xy - 3 = 0. If λ1 > 0 and λ2 > 0, then x + y - 1 = 0 and xy - 3 = 0. If λ1 > 0 and λ2 = 0, then x + y - 1 = 0. If λ1 = 0 and λ2 > 0, then xy - 3 = 0. We now consider each case separately. Case 1: λ1 > 0 and λ2 > 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have the following possibilities: x + y - 1 = 0, xy - 3 ≤ 0 (i.e., xy = 3), λ1 > 0, λ2 > 0 x + y - 1 ≤ 0, xy - 3 = 0 (i.e., x = 3/y), λ1 > 0, λ2 > 0 x + y - 1 = 0, xy - 3 = 0 (i.e., x = y = √3), λ1 > 0, λ2 > 0 We can exclude the second case because it violates the constraint x, y ≥ 0. The first and third cases satisfy all the Kuhn-Tucker conditions, and we can check that they correspond to local minima of f subject to the constraints. For the first case, we have x = y = √3/2 and f(x, y) = -1/2. For the third case, we have x = y = √3 and f(x, y) = -2. Case 2: λ1 > 0 and λ2 = 0From λ1(x + y - 1) = 0, we have x + y - 1 = 0 (because λ1 > 0). From the first Kuhn-Tucker condition, we have 4x - 2y - λ1 = λ1y. Since λ1 > 0, we can solve for y to get y = (4x - λ1)/(2 + λ1). Substituting this into the constraint x + y - 1 = 0, we get x + (4x - λ1)/(2 + λ1) - 1 = 0. Solving for x, we get x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4. We can check that this satisfies all the Kuhn-Tucker conditions for λ1 > 0, and we can also check that it corresponds to a local minimum of f subject to the constraints. For this value of x, we have y = (4x - λ1)/(2 + λ1), and we can compute f(x, y) = -3/4 + (5λ1^2 + 4λ1 + 1)/(2(2 + λ1)^2). Case 3: λ1 = 0 and λ2 > 0From λ2(xy - 3) = 0, we have xy - 3 = 0 (because λ2 > 0). Substituting this into the constraint x + y - 1 ≥ 0, we get x + (3/x) - 1 ≥ 0. This implies that x^2 + (3 - x) - x ≥ 0, or equivalently, x^2 - x + 3 ≥ 0. The discriminant of this quadratic is negative, so it has no real roots. Therefore, there are no feasible solutions in this case. Case 4: λ1 = 0 and λ2 = 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have x + y - 1 ≤ 0 and xy - 3 ≤ 0. This implies that x, y > 0, and we can use the first and second Kuhn-Tucker conditions to get 4x - 2y = 0 2y - 2x = 0 x + y - 1 = 0 xy - 3 = 0 Solving these equations, we get x = y = √3 and f(x, y) = -2. (b) Show that the minimal point does not have x=0.To show that the minimal point does not have x=0, we need to find the optimal value of x that minimizes f subject to the constraints and show that x > 0. From the Kuhn-Tucker conditions, we know that the optimal value of x satisfies one of the following conditions: x = y = √3/2 (λ1 > 0, λ2 > 0) x = √3 (λ1 > 0, λ2 > 0) x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4 (λ1 > 0, λ2 = 0) If x = y = √3/2, then x > 0. If x = √3, then x > 0. If x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4, then x > 0 because λ1 ≥ 0.
To know more about constraints, visit:
https://brainly.com/question/17156848
#SPJ11
11. Three forces act on a body. A force of 70 N acts toward the south, a force of 90 N acts toward the west, and a force of 100 N acts at S10°E. Determine the magnitude and direction of the resultant force of these three forces. [6 marks] Magnitude of resultant force is Direction of resultant force is 12. A pilot flies her plane on a heading of N25°E with an air speed of 290 km/h. The wind speed is 75 km/h from the N70°W. Calculate the ground velocity of the plane.[6 marks]
Answers
11. The magnitude of the resultant force is approximately 78.1 N, and the direction is approximately S21.1°W.
12. The ground velocity of the plane is approximately 292.6 km/h.
What is the magnitude of the resultant forces?11. To determine the magnitude and direction of the resultant force, we can use vector addition. We'll add the three given forces using their respective components.
Let's break down the given forces into their horizontal (x-axis) and vertical (y-axis) components:
Force 1 (70 N towards the south):
Horizontal component: 0 N
Vertical component: -70 N
Force 2 (90 N towards the west):
Horizontal component: -90 N
Vertical component: 0 N
Force 3 (100 N at S10°E):
To find the components of this force, we'll use trigonometry. The angle S10°E can be broken down into two components:
- South component: 100 N × cos(10°)
- East component: 100 N × sin(10°)
South component: 100 N × cos(10°) ≈ 98.5 N
East component: 100 N × sin(10°) ≈ 17.3 N
Now we can calculate the total horizontal and vertical components by summing up the individual components:
Total horizontal component = -90 N + 17.3 N = -72.7 N
Total vertical component = -70 N + 98.5 N = 28.5 N
To find the magnitude of the resultant force, we'll use the Pythagorean theorem:
Magnitude = √((Total horizontal component)² + (Total vertical component)²)
Magnitude = √((-72.7 N)² + (28.5 N)²)
Magnitude ≈ √(5285.29 N² + 812.25 N²)
Magnitude ≈ √(6097.54 N²)
Magnitude ≈ 78.1 N (rounded to one decimal place)
To find the direction of the resultant force, we'll use trigonometry:
Angle = tan^(-1)((Total vertical component) / (Total horizontal component))
Angle = tan^(-1)((28.5 N) / (-72.7 N))
Angle ≈ tan^(-1)(-0.392)
Angle ≈ -21.1° (rounded to one decimal place)
Since the angle is negative, we can interpret it as 21.1° clockwise from the positive x-axis. Therefore, the direction of the resultant force is approximately S21.1°W.
12. To calculate the ground velocity of the plane, we need to consider the vector addition of the plane's airspeed and the wind velocity.
First, let's break down the given information:
- Airspeed of the plane: 290 km/h on a heading of N25°E
- Wind speed: 75 km/h from the N70°W
Now, let's calculate the components of the airspeed and wind velocity:
Airspeed component:
- North component: 290 km/h × cos(25°)
- East component: 290 km/h × sin(25°)
North component of airspeed = 290 km/h × cos(25°) ≈ 262.34 km/h
East component of airspeed = 290 km/h × sin(25°) ≈ 122.08 km/h
Wind velocity component:
- North component: 75 km/h × cos(70°)
- West component: 75 km/h × sin(70°)
North component of wind velocity = 75 km/h × cos(70°) ≈ 25.70 km/h
West component of wind velocity = 75 km/h × sin(70°) ≈ 71.86 km/h
To calculate the ground velocity, we'll add the components of the airspeed and wind velocity:
North component of ground velocity = North component of airspeed + North component of wind velocity
North component of ground velocity = 262.34 km/h + 25.70 km/h = 288.04 km/h
East component of ground velocity = East component of airspeed - West component of wind velocity
East component of ground velocity = 122.08 km/h - 71.86 km/h = 50.22 km/h
Now, we can calculate the magnitude of the ground velocity using the Pythagorean theorem:
Magnitude of ground velocity = √((North component of ground velocity)² + (East component of ground velocity)²)
Magnitude of ground velocity = √((288.04 km/h)² + (50.22 km/h)²)
Magnitude of ground velocity ≈ √(82994.8816 km²/h² + 2522.0484 km²/h²)
Magnitude of ground velocity ≈ √(85516.93 km²/h²)
Magnitude of ground velocity ≈ 292.6 km/h
learn more on resultant force here;
https://brainly.com/question/24524696
#SPJ4
If your original network address with prefix is 172.16.0.0/16, what should your new network address with prefix be if you need 16 subnets?
Answers
172.16.0.0/20 is the required network address with a prefix if you need 16 subnets.
Given that,
If you require 16 subnets, your new network address with a prefix should be something different from the old one, which is 172.16.0.0/16. To determine the prefix corresponding to the 16 subnets.
Here,
Original network address with a prefix = 172.16.0.0/16,
After 16 subnets the address would become,
New network address with the prefix with 16 subnets = 172.16.0.0/20.
172.16.0.0/20 is the required new address with prefix be if you need 16 subnets.
Learn more about arithmetic here:
brainly.com/question/14753192
#SPJ1
9) using opposite operations, solve for m
4m+8=12
Answers
Answer: 1
Step-by-step explanation:
4m + 8 = 12
=> 4m = 4
=> m = 1
Answer:
Subtract 8 from both sides now your left with 4m and 4. Divide 4 from both sides to get 1. 1 is your answer
I urgently need help with this, I need the code.

Answers
Answer:
Try 34697
If it's correct can I get the Brainlest
Plzzz help pls I really need this 9th grade math

Answers
Answer:
1/3
with indices, the brackets mean you multiply the powers - so you need to multiply 1/4 by something to get 1/12, which is 1/3
:)
2.1Simplifying Expressions: Problem 1 (1 point) Simplify the following expression. 6- 4(x - 5)-
Answers
The simplified expression is 26 - 4x.
To simplify the expression 6 - 4(x - 5), we can apply the distributive property and simplify the terms.
6 - 4(x - 5)
First, distribute -4 to the terms inside the parentheses:
6 - 4x + 20
Now, combine like terms:
(6 + 20) - 4x
Simplifying further:
26 - 4x
Therefore, the simplified expression is 26 - 4x.
Learn more about distributive property here
https://brainly.com/question/12192455
#SPJ11
Is the statement at the top true or false

Answers
Answer:
false
Step-by-step explanation:
these angles are horizonal
in 1970, 590 students among 1000 randomly selected college freshmen thought that capital punishment should be abolished. in 2005, 350 students among 1000 randomly selected college freshmen thought that capital punishment should be abolished. what is the two-sample z test statistic for evaluating the null hypothesis that the percentage of students who support capital punishment did not change from 1970 to 2005? round your answer to two decimal places.
Answers
The two-sample z-test statistic for evaluating the null hypothesis that the percentage of students who support capital punishment did not change from 1970 to 2005 is -4.08 (rounded to two decimal places).
To calculate the two-sample z-test statistic, we need to compare the proportions of students who support capital punishment in 1970 and 2005. The null hypothesis states that the percentage of students who support capital punishment did not change.
Let p1 be the proportion of students who support capital punishment in 1970, and p2 be the proportion in 2005. We can calculate the sample proportions as p1 = 590/1000 = 0.59 and p2 = 350/1000 = 0.35.
The formula for the two-sample z-test statistic is given by z = (p1 - p2) / sqrt((p(1 - p)(1/n1 + 1/n2))), where p is the pooled proportion and n1 and n2 are the sample sizes.
To calculate p, we compute the pooled proportion as p = (p1n1 + p2n2) / (n1 + n2) = (0.591000 + 0.351000) / (1000 + 1000) = 0.47.
Substituting the values into the formula, we have z = (0.59 - 0.35) / sqrt((0.47*(1 - 0.47)(1/1000 + 1/1000))) = -4.08.
Therefore, the two-sample z-test statistic for evaluating the null hypothesis is -4.08 (rounded to two decimal places).
Learn more about z-test statistic here:
https://brainly.com/question/30754810
#SPJ11
What is the slope of the line that is PARALLEL to the line 4x + 2y = 15?
Answers
Answer:
\(2y = - 4x + 15 \\ y = - 2x + 7.5 \\ \\ slop \: is \: x \: factor \: - 2\)
Transcribed image text: The probability distribution for the random variable x follows. x f(x) 20 0.30 25 0.15 30 0.20 35 0.35 (a) Is this probability distribution valid? Explain. Since f(x) 0 for all values of x and rx) = 1 , this is a proper probability distribution. (b) What is the probability thatx30? (c) What is the probability that x is less than or equal to 25? (d) What is the probability that x is greater than 30?
Answers
a. The probability distribution is valid because the probabilities (f(x)) are non-negative for all values of x, and the sum of all probabilities is equal to 1.
b. The probability that x 30 is 20%.
c. The probability that x is less than or equal to 25 is 45%.
d. The probability that x is greater than 30 is 35%.
(a) The probability distribution is valid because the probabilities (f(x)) are non-negative for all values of x, and the sum of all probabilities is equal to 1. This is indicated by the statement "rx) = 1", which means the sum of all probabilities is 1.
(b) The probability that x = 30 is given by f(30) = 0.20. Therefore, the probability that x = 30 is 0.20 or 20%.
(c) To find the probability that x is less than or equal to 25, we need to sum the probabilities of all values of x that are less than or equal to 25. In this case, we need to sum the probabilities of x = 20 and x = 25:
P(x ≤ 25) = f(20) + f(25) = 0.30 + 0.15 = 0.45 or 45%.
(d) To find the probability that x is greater than 30, we need to sum the probabilities of all values of x that are greater than 30. In this case, we need to sum the probability of x = 35:
P(x > 30) = f(35) = 0.35 or 35%.
Therefore, the probability that x is greater than 30 is 0.35 or 35%.
Learn more about probability at https://brainly.com/question/15135952
#SPJ11
Exercise 10
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. What is the probability of the compound event? Write your answer as a fraction or percent rounded to the nearest tenth.

Answers
The probability of choosing a 5 and then a 6 is 1/49
Finding the probability of the compound eventFrom the question, we have the following parameters that can be used in our computation:
The tiles
Where we have
Total = 7
The probability of choosing a 5 and then a 6 is
P = P(5) * P(6)
So, we have
P = 1/7 * 1/7
Evaluate
P = 1/49
Hence, the probability of choosing a 5 and then a 6 is 1/49
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
Question
You randomly choose one of the tiles. Without replacing the first tile, you choose a second tile. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth. The probability of choosing a 5 and then a 6
You are designing a 5 kilometer course for a local charity run. your assistants provide you with the following measures in yards. you need to convert the distances to kilometers, and then tell your assistants how much further they need to extend the finish line to complete the course.
course streets distance
main street to 6th ave. 781 yards
6th ave. to pleasant road 1,250 yards
pleasant road to city park 275 yards
route through city park 2,337 yards
city park to main street 725 yards
Answers
You are designing a 5 kilometer course for charity run. The design now has been covers 4,908.5 meters, hence, you need to add more 91.5 meters on the course.
The conversion from yard to meter is:
1 yard = 0.9144 meters
The course streets and the distances after converted into meters are:
main street to 6th ave. 781 yards = 714.15 meters
6th ave. to pleasant road 1,250 yards = 1143 meters.
pleasant road to city park 275 yards = 251.46 meters
route through city park 2,337 yards = 2,136.95 meters
city park to main street 725 yards = 662.94 meters
Total course = 714.15 + 1143 + 251.46 + 2,136.95 + 662.94
Total course = 4,908.5 meters
The design is 5 km = 5000 meters. Therefore, you still need to add:
5000 - 4,908.5 = 91.5 meters more course.
Learn more about measurement unit here:
https://brainly.com/question/7716790
#SPJ4
PLEASE HELP ASAP!!!
3 + 2x² + 3x + 2x² + 5 = ?
Answers
Answer: 4x² + 3x + 8
Work: I combined Like Terms, put them in the right form, from the x² to the number.
I hope this helps and Happy Holidays! :)
Answer:
25
Step-by-step explanation:
3+2=5×2 ×2 +5=25
add the 10 to the other 10 and then add 5
anybody can cooperate with me? In making a presentation. I need someone good in slides?
Answers
Sure what do you need
The number of bacteria in a bacterial culture increased by 149% in 110 hours. How many bacteria were there after 55 hours if there were 4850 pcs. from the beginning?
Round the answer to whole tens.
a. 8980 pcs
b. 7650 pcs
c. 7890 pcs
d. 7760 pcs

Answers
The mass of a radioactive substance follows a continuous exponential decay model, with a decay rate parameter of 3.9% per day. Find the half-life of this substance (that is, the time it takes for one-half the original amount in a given sample of this substance to decay).
Answers
The half-life of the substance is approximately 17.78 days.
The exponential decay model for the mass of the substance can be written as:
\(m(t) = m0 \times e^{(-rt)},\)
where m0 is the initial mass, r is the decay rate parameter (as a decimal), and t is time in days.
If we want to find the half-life of the substance, we need to find the value of t when the mass has decreased to half of its original value (m0/2). In other words, we need to solve the equation:
m(t) = m0/2
\(m0 \times e^{(-rt)} = m0/2\)
\(e^{(-rt) }= 1/2\)
Taking the natural logarithm of both sides, we get:
-ln(2) = -rt
t = (-ln(2)) / r
Substituting the value of r (0.039), we get:
t = (-ln(2)) / 0.039
t ≈ 17.78 days
for such more question on substance
https://brainly.com/question/27641723
#SPJ11
HELP NOW FOR MEGA POINTS
Which statement below about the graph of f(x)=-log(x+4)+2 is true?
1) f(x) has a y-intercept at (0,2)
2) −f(x) has a y-intercept at (0,2)
3) As x → ∞, f(x) → ∞.2)
4) x → −4, f(x) → ∞
SHOW WORK
Answers
Answer:
4 IS THE ANSWER MATE
Step-by-step explanation:
Absolutely, I can do that!
Let's take a look at each statement:
1) f(x) has a y-intercept at (0,2)
To find the y-intercept, we need to set x to 0 and solve for y. Plugging in x = 0 into the equation for f(x), we get:
f(0) = -log(0+4) + 2
f(0) = -log(4) + 2
f(0) = -0.602 + 2
f(0) = 1.398
Since the y-coordinate of the y-intercept is 1.398, not 2, this statement is false.
2) The function -f(x) has a y-intercept at (0,2)
Since the negative sign in front of f(x) reflects the graph of f(x) across the x-axis, we can determine the y-intercept of -f(x) by taking the opposite of the y-intercept of f(x). Since the y-intercept of f(x) is not 2, this statement is also false.
3) As x approaches positive infinity, the function f(x) approaches negative infinity.
The function f(x) is a logarithmic function with a negative coefficient, which means it approaches negative infinity as x approaches positive infinity. Therefore, this statement is true.
4) As x approaches -4 from the right, the function f(x) approaches negative infinity.
As x approaches -4 from the right, the value of f(x) becomes more and more negative without bound, which means that f(x) approaches negative infinity as x approaches -4 from the right. Therefore, this statement is also true.
In summary, statements (1) and (2) are false, while statements (3) and (4) are true.
Question 7
1 pts
Dan has a conical lamp shade with an altitude of 6 inches and a diameter of 12
inches. How much material is needed to make the lampshade?
6 in.
1
--12 in.
Answers
Then multiple by hight or altitude to get surface area ( circumference x height)
SA =72pi or ~226.19 in^2
If you are putting material on the top of lamp to, add pi(r)^2 or 36pi= ~113.10 in^2
Nate tosses a ball up a hill for his dog to chase. The path of the ball is modeled by the function y = –14x2 + 335x, where x is the ball’s horizontal distance from Nate in feet and y is the ball’s height in feet. The hill is modeled by the line y = 15x. How far does the ball travel horizontally before it hits the ground?
Answers
Answer:
The horizontal distance the ball travels before it hits the ground is 22.\(\overline{857142}\) feet
Step-by-step explanation:
The given parameter are;
The function modelling the path of the ball tossed by Nate y = -14·x² + 335·x
x = The horizontal distance the ball travels from Nate in feet
y = The height of the ball in feet
The line equation modelling the hill is y = 15·x
The point where the ball hits the ground is given by the point the graph of the equation for the path of the ball and the path of the model of the line of the hill meet as follows;
Ball path is y = -14·x² + 335·x
Hill path is y = 15·x
The point both paths meet and the ball hits the ground is -14·x² + 335·x = 15·x
Which gives;
-14·x² + 335·x - 15·x = 0
-14·x² + 320·x = 0
320·x - 14·x² = 0
x × (320 - 14·x) = 0
x = 0, or x = 320/14 = 22 6/7 = 22.\(\overline{857142}\) feet
Therefore;
The horizontal distance the ball travels before it hits the ground = x = 22.\(\overline{857142}\) feet.
The path of ball will be parabolic in nature .Parabolic path is defined as the angle of trajectory of a projectile.
Ball travel 22.86 feet horizontally before it hits the ground.
Since, The path of the ball is modeled by the function \(y = -14x^{2} + 335x\)
where x is the ball’s horizontal distance from Nate in feet and y is the ball’s height in feet.
And hill is modeled by equation, \(y=15x\)
To find out how much ball will travel horizontally before it hits ground , we have to find intersection of given two model equation.
\(y = -14x^{2} + 335x\)
\(y=15x\)
So, \(-14x^{2} + 335x=15x\\\\-14x^{2} + 335x - 15x = 0\\\\320x - 14x^{2} = 0\\\\x(320-14x)=0\\\\x=0, x=320/14=22.86\)
Thus, Ball travel 22.86 feet horizontally before it hits the ground.
Learn more:
https://brainly.com/question/24658194
Which equation can be used to check whether 18 ÷ 6 = 148 ?
48 ÷ 6 = 48
8 × 6 = 48
1/48 × 6 = 1/8
1/48 × 1/8 = 1/384
Answers
Answer:
8 x 6
Step-by-step explanation:
Pls tell the answer for 50 points!

Answers
Answer:
7*11^5
Explanation:
(the photo)

You format a document in three columns of equal width. The document is 8.5 in. wide. You want left and right margins of 1 in. each. Between the columns there is a "gutter" that is one eighth as wide as each column. What is the width of each column?
Answers
The width of each column is 2 inches.
Width is the measurement of something from side to side.
Let x = width of each column.
If a "gutter" is one eighth as wide as each column, then the width of the gutter can be expressed as
gutter = (1/8)x
If the document is 8.5 in. wide, then the sum of the widths of the left and right margins, the 3 columns and the 2 gutters in between columns is equal to 8.5 in.
left margin + right margin + 3 columns + 2 gutters = 8.5in
1 in + 1 in + 3x + 2(1/8)x = 8.5 in
3x + 2(1/8)x = 8.5 in - 1 in - 1 in
3 1/4 x = 6.5 in
x = 2 in
width of each column = 2 inches
Learn more about width here: https://brainly.com/question/11434049
#SPJ4
I need the answerrrrrrrr plsssssssss

Answers
Answer:
Hope this helps
Step-by-step explanation:
Range: 6
Number of students with 6 siblings: 1
Number of students with no siblings: 3
Number of students with 3 or more siblings: 11
Number of observations: 20
Shape of the data: Left skewed
two families with four people in each family go to a movie theater. in how many ways can they be seated
Answers
According to probability, if both families want to sit together, they can be seated in a row a maximum of two times.
What seating configuration?The direction that each person is facing is crucial when arranging the people.
In order to determine how many ways they can be seated in a row if both families want to sit together, imagine that two families with four members each attend a movie theatre.
Given that the arrangement is important, we will apply the permutation rule. We'll divide the remaining four into two groups of four each.
There are two different ways to arrange the groups so they can sit together.
2! = 2 * 1
2! = 2ways
To know more about probability visit:-
brainly.com/question/11234923
#SPJ4
Please give me more points so i can get help

Answers
Answer:
15°
Step-by-step explanation:
angle FGH = angle HGI ( since GH bisects angle FGI)
that means
(2x + 1) = (3x - 9)
= -x = -8
x = 8
angle HGI = (3x - 9)
= 3(8) - 9
24 - 9
= 15°
Answer:
21
Step-by-step explanation:
To find the measure of <HGI we first need to find the value of x
GH bisects angle <FI which means it divided the angle into two equal parts:
<FGH = <HGI
2x + 1 = 3x - 9 transfer like terms to the same side of the equation
1 + 9 = 3x - 2x
10 = x now replace x with 10
3*10 - 9 = 21
find a positive and negative coterminal angle for 250 degrees
Answers
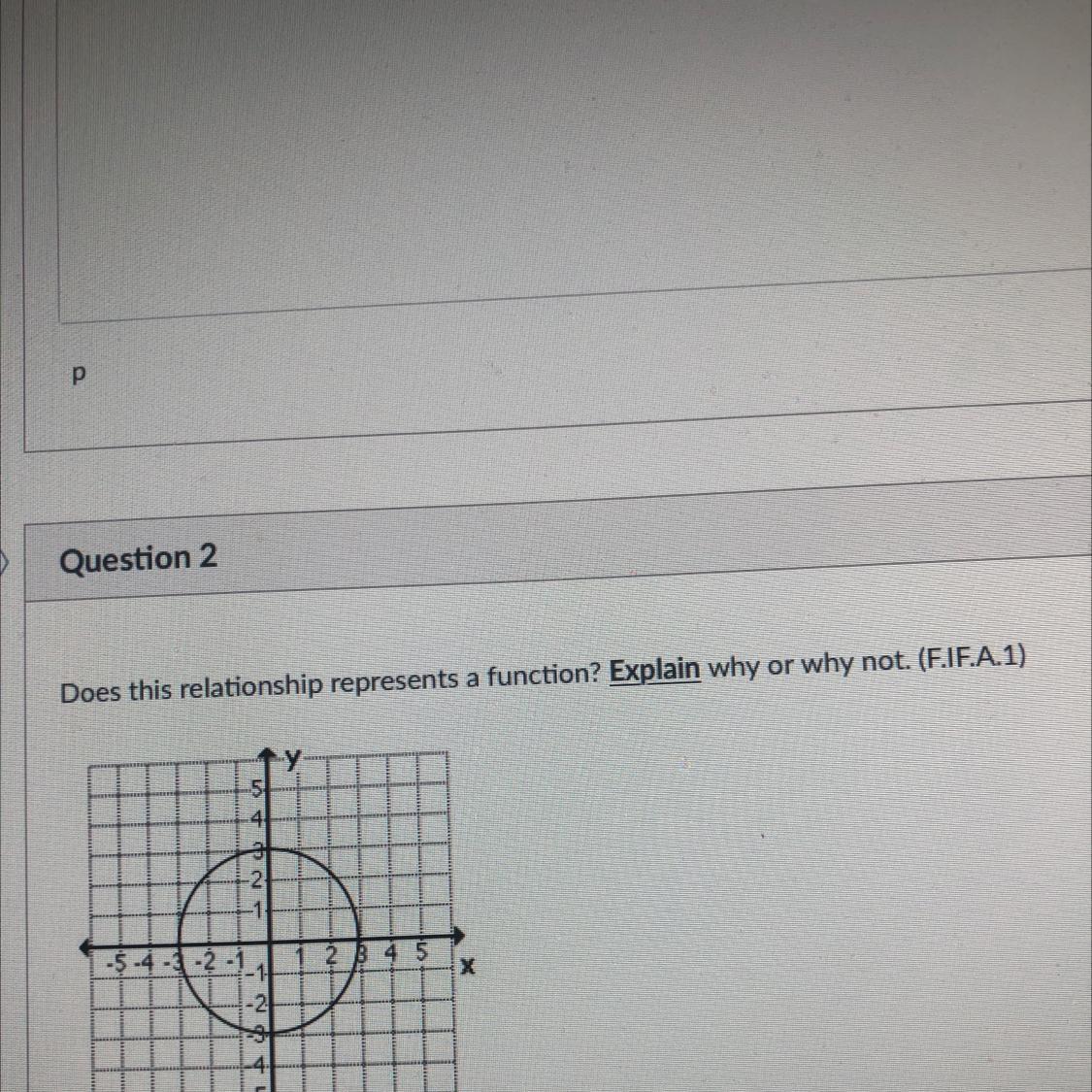
Does this relationship represents a function? Explain why or why not. (F.IF.A.1)
y
-5
4
-2
-5.4
-2.1
2 B4
5
X
Edit
View
Insert
Format
Tools Table HELP PLEASE
Answers
Step-by-step explanation:
no, it does not.
because almost every valid value of x (from -3 to +3) has 2 associated result values of y.
like x = 0 has y = 3 and y = -3.
but for a function there can be only ONE associated y value for every valid x value.
