Answers
Answer:
I believe answer B
Step-by-step explanation:
It says shifted UP 3 units and 2+3=5 so that is my answer. Feel free to yell at me if I am wrong.
Related Questions
What is 4(x-7)=2(x+3)?
Answers
Answer:
Isolate the variable by dividing each side by factors that don't contain the variable.
4(x−7)=2(x+3)
Simplify both sides of the equation.
4(x−7)=2(x+3)
4x+−28=2x+6
4x−28=2x+6
Subtract 2x from both sides.
4x−28−2x=2x+6−2x
x−28=6
Add 28 to both sides.
2x−28+28=6+28
2x=34
Divide both sides by 2.
2x/2 = 34/2
x = 17
Answer:
x = 17
Step-by-step explanation:
\(4(x-7)=2(x+3)\\\\4x-28=2x+6\\\\4x-28+28=2x+6+28\\\\4x=2x+34\\\\4x-2x=2x-2x+34\\\\2x=34\\\\\frac{2x=34}{2}\\\\ \boxed{x=17}\)
Hope this helps.
At the end of 1st Quarter of 2009 the median price of a single-family home in Charleston/No. Charleston was $184,990. Single-family home prices in Charleston/No. Charleston decreased from the 1st Qtr of 2008 by 8.15%. NOTE: Depreciation means a negative value for r. (a). Estimate the median price of a single-family home in the 1st Qtr of 2008.
(b). If the median price of a single-family home falls at the same rate for the next 2 years, estimate the median price of a single-family home in the 1st Qtr of 2011.
Answers
The estimated median price of a single-family home in Charleston/No. Charleston in the 1st Quarter of 2008 is $201,048. If the median price continues to decrease at the same rate for the next two years, the estimated median price of a single-family home in the 1st Quarter of 2011 would be $144,458.
(a) To estimate the median price of a single-family home in the 1st Quarter of 2008, we need to calculate the original price before the 8.15% decrease. Let's assume the original price was P. The price after the decrease can be calculated as P - 8.15% of P, which translates to P - (0.0815 * P) = P(1 - 0.0815). Given that the end of 1st Quarter of 2009 median price was $184,990, we can set up the equation as $184,990 = P(1 - 0.0815) and solve for P. This gives us P ≈ $201,048 as the estimated median price of a single-family home in the 1st Quarter of 2008.
(b) If the median price of a single-family home falls at the same rate for the next two years, we can calculate the price for the 1st Quarter of 2011 using the estimated median price from the 1st Quarter of 2009. Starting with the median price of $184,990, we need to apply an 8.15% decrease for two consecutive years. After the first year, the price would be $184,990 - (0.0815 * $184,990) = $169,805.95. Applying the same percentage decrease for the second year, the price would be $169,805.95 - (0.0815 * $169,805.95) = $156,012.32. Therefore, the estimated median price of a single-family home in the 1st Quarter of 2011 would be approximately $144,458.
To learn more about median click here: brainly.com/question/300591
#SPJ11
Which equation best represents the
line on the graph?
A y = 3x - 9
B y = -3x + 9
C y = -3x - 3
D y = 5x + 3
Answers
Answer:
answer is b
Step-by-step explanation:
Identify the graph of the inequality 2(2x - 1) + 7 < 13 or -2x + 55-10.
--
5 10
-10
-5
0
+
-10
OL
0
-5
5
10
-+
5 10
-10
5
0
DONE

Answers
Answer:
The answer is the last one.
Step-by-step explanation:
Firstly, look at the first inequality and we get \(4x+5<13\), so \(x<2\). In the second inequality, we have \(15\leq 2x\), so \(x\ge 7.5\). Together, we know that the answer is the last one.
the model of a river is constructed to a scale of 1/60. if the water in the river is flowing at 38 ft/s, how fast must the water flow in the model?
Answers
The water in the given model must flow at a constant speed of 2,280 ft/s to represent the actual water flow of 38 ft/s.
The speed of water flow in the model can be calculated as follows:
Model speed = Actual speed / Scale factor
Since the scale factor is 1/60, the model speed will be:
Model speed = 38 ft/s / (1/60) = 2,280 ft/s
Therefore, the water in the given model must flow at a constant speed of 2,280 ft/s to accurately and precisely represent the actual water flow of 38 ft/s.
Note: The calculated model speed seems unreasonably high, and it is likely that there is an error in the given values or in the calculation.
Learn more about Speed
https://brainly.com/question/4931057
#SPJ4
I will mark brainliest but only if you answer correctly and I will report if you don’t actually give an answer

Answers
Answer:
Choice D
y = 3(2/3)^x
Step-by-step explanation:
a) y = 2(3/2)^x = 3^x (pretty close)
b) y = (2/3)^x (wrong, coming from the wrong side)
c) y = 2(3)^x = 6^x (too close to y line)
d) y = 3(2/3)^x = 2^x (looks right)
multiple regression analysis: a) establishes a cause and effect relationship. b) does not produce measures of probable error. c) measures the change in one variable associated with the change in one other variable only. d) measures the change in one variable associated with the change in more than one other variable
Answers
The change in one variable related to the change in more than one other variable is measured using multiple regression analysis.
A statistical method known as multiple regression is used on datasets intended to show a link between a single response or dependent variable and a number of independent factors.
Even though linear regression is frequently employed, it can only be utilized with one independent variable and one dependent variable. Non-linear regression is not predicted by linear regression, which is also limited to the training dataset.
We employ multiple regression to account for the same restrictions. It focuses on removing one particular limitation, which is allowing for the analysis of multiple independent variables.
Visit the link below to learn more about linear regression:
brainly.com/question/28558779
#SPJ4
You win $10 000 in a Best Math Student competition. Being a generous person, you decide to invest the money in two local businesses to help them get off the ground. The businesses are Paul’s Paper and Tiffany’s Tyres. They offer the following annual interest rates return to encourage your investment;
PP – 10% p.a.
TT – 5% p.a.
The investment's combined return is $620 after one year. How much was invested in each company?
Answers
The amount invested in each company is :
Amount invested in PP = $2400Amount invested in TT = $(10000 - 2400) = $7600Using the simple interest relation:
Simple interest = principal × rate × time
Total amount = 10000
Let :
principal invested in PP = r
HENCE, amount invested in TT = 10000 - r
Total interest earned on both investments = $620
PP investment return + TT investment return = 620
(r × 10% × 1) + (10000 - r × 5% × 1) = 620
0.1r + 500 - 0.05r = 620
0.05r = 620 - 500
0.05r = 120
r = 120 / 0.05
r = 2400
Hence,
Amount invested in PP = $2400
Amount invested in TT = $(10000 - 2400) = $7600
Learn more : https://brainly.com/question/20014745?referrer=searchResults
Identify the surface with the given vector equation. r(s, t) = (s cos(t), s sin(t), s) circular paraboloid O elliptic cone O hyperbolic paraboloid O plane O circular cone X
Answers
The surface with the given vector equation, r(s, t) = (s cos(t), s sin(t), s), is a circular cone.
The vector equation r(s, t) = (s cos(t), s sin(t), s) represents a surface in three-dimensional space. Let's analyze the equation to determine the nature of the surface.
In the equation, we have three components: s, cos(t), and sin(t). The presence of s indicates that the surface expands or contracts radially from a central point. The trigonometric functions cos(t) and sin(t) determine the angle at which the surface extends in the x and y directions.
By observing the equation closely, we can see that as s increases, the radius of the surface expands uniformly in all directions, while the height remains constant. This behavior is characteristic of a circular cone. The circular base of the cone is defined by s cos(t) and s sin(t), and the vertical component is determined by s.
Therefore, the surface described by the vector equation r(s, t) = (s cos(t), s sin(t), s) is a circular cone.
Learn more about vector equation here :
https://brainly.com/question/32619742
#SPJ11
a middle school with s students ran a survey to determine the students favorite activities the table indicates the number of students who enjoy each activity answer parts a and b

Answers
The expressions that show the number of students for each activity are;
Dance; (1/7)z + 22Baseball; (4/7)z - 24Drama; (1/7)z + 26What is a Set?A set contains elements or members that can be mathematical objects of any kind, including numbers, symbols, points in space, lines, other geometric shapes, variables, or even other sets.
A set is a mathematical model for a collection of various things.
We are given;
Total number of students in the middle school = z
A) From the given table, we can deduce that;
Students that like dance activity = (1/7)z + 22Students that like baseball activity = (4/7)z - 24Students that like drama = (1/7)z + 26B; Now, the expression to show the students that like either drama or dance is;
(1/7)z + 26 + (1/7)z + 22
>> (2/7)z + 48
Read more about sets here:
https://brainly.com/question/13458417
#SPJ1
A middle school with z students ran a survey to determine the students' favorite activities. The table indicates the number of students who enjoy each activity. Answer parts A and B.
Table:
Activity:
Dance- 22 more than one-seventh of the students
Baseball- 24 fewer than four-sevenths of the students
Drama- 26 more than one-seventh of the students.
91) __________ involves the analysis of accumulated data and involves a __________. a) OLAP, database b) OLAP, data warehouse c) OLTP, database d) OLTP, data warehouse
Answers
OLAP is used for the analysis of accumulated data, and it requires a data warehouse.
while OLTP is used for transaction processing and requires a database optimized for real-time transaction processing. The analysis of accumulated data is known as Online Analytical Processing (OLAP), and it involves a data warehouse. OLAP is a business intelligence tool used for multi-dimensional analysis of large data sets, while a data warehouse is a central repository that stores historical and current data from multiple sources in a structured manner. OLAP allows users to perform complex queries on large data sets, analyze trends, and make informed business decisions. It is often used in data mining and decision support systems. OLAP tools can be used to slice and dice data, drill down to more detailed data, and roll up to higher levels of summary data. OLAP is primarily used for analytical purposes and is not designed for transaction processing. On the other hand, a data warehouse is designed to support OLAP and is used for storing large amounts of historical data that can be queried and analyzed. Data is extracted from various sources, transformed, and loaded into the data warehouse in a structured format, enabling efficient querying and analysis. OLTP (Online Transaction Processing), on the other hand, is a type of transaction processing that is designed for processing real-time transactions in databases. It is used for day-to-day operations such as order processing, inventory management, and customer management. OLTP is optimized for processing large volumes of transactions in real-time, and is not suitable for analytical purposes.
In summary, OLAP is used for the analysis of accumulated data, and it requires a data warehouse, while OLTP is used for transaction processing and requires a database optimized for real-time transaction processing.
To know more about accumulated data click here:
brainly.com/question/29638039
#SPJ4
.
x + 3y = 25
2x + y = 15
Answers
Answer: x=4 and y=7
Step-by-step explanation: x+3y=25
x+3y+−3y=25+−3y(Add -3y to both sides)
x=−3y+25
Find the volume of the pyramid with a square base where the perimeter of the base is 8. 7cm and height of the pyramid is 6. 3cm round your answer to the nearest tenth of the cubic centimeter
Answers
Answer:
9.9\(cm^{3}\)
Step-by-step explanation:
Formula:
1/3(area of the base x height)
1/3 [2.175(2.175)(6.3)]
1/3(4.730625)(6.3)
1/3(29.8029375)
9.9343125
Is the perimeter of the base is 8.7, we need to divide that by 4 (2.175) to find out the side length of the square. The area of the square, we need to multiply 2.175 by 2.175.
9.9343125 rounded to the nearest tenth is 9.9
Helping in the name of Jesus.
Gravel is being dumped from a conveyor belt at a rate of 20 cubic feet per minute. It forms a pile in the shape of a right circular cone whose base
diameter and height are always the same. How fast is the height of the pile increasing when the pile is 14 feet high? Recall that the volume of a
right circular cone with height h and radius of the base r is given by V=pi/3 r²h.
Your answer: ______
feet per minute.
Answers
Answer:
The height of the pile is increasing at a rate of 16.72 feet per minute. To solve this problem, we need to use the volume formula for a right circular cone: V=pi/3 r²h. We know that the volume is 20 cubic feet per minute, the height is 14 feet and the radius of the base is 14 feet. So we can calculate the rate of change of the height by rearranging the formula to give v/(pi/3r²). So for our example, v/(pi/3*14²)=20/(pi/3*14²)=20/(3.14*196)=20/613.44=16.72 feet per minute.
(a) minimize the perimeter of rectangles with area 25 cm^2. (b) is there a maximum perimeter of rectangles with area 25 cm^2?
Answers
a. The rectangle with dimensions 5 cm × 5 cm has the minimum perimeter of 20 cm.
b. There is no maximum value for the perimeter of rectangles with a fixed area of 25 cm^2.
(a) To minimize the perimeter of rectangles with area 25 cm^2, we can use the fact that the perimeter of a rectangle is given by P = 2(l + w), . We want to minimize P subject to the constraint that lw = 25.
Using the constraint to eliminate one variable, we have:
l = 25/w
Substituting into the expression for the perimeter, we get:
P = 2(25/w + w)
To minimize P, we need to find the value of w that minimizes this expression. We can do this by finding the critical points of P:
dP/dw = -50/w^2 + 2
Setting this equal to zero and solving for w, we get:
-50/w^2 + 2 = 0
w^2 = 25
w = 5 or w = -5 (but we discard this solution since w must be positive)
Therefore, the width that minimizes the perimeter is w = 5 cm, and the corresponding length is l = 25/5 = 5 cm. The minimum perimeter is:
P = 2(5 + 5) = 20 cm
So the rectangle with dimensions 5 cm × 5 cm has the minimum perimeter of 20 cm.
(b) There is no maximum perimeter of rectangles with area 25 cm^2. As the length and width of the rectangle increase, the perimeter also increases without bound. Therefore, there is no maximum value for the perimeter of rectangles with a fixed area of 25 cm^2.
To know more about perimeter of rectangles refer here:
https://brainly.com/question/29595517
#SPJ11
If the square root of 5 = x + 3, what is the value of (x + 3)^2?
*Brainliest*
Answers
For the irrational number x + 3 = √5, the value of the algebraic equation y = (x + 3)² is equal to 5.
How calculate the value of an algebraic equation in terms of an irrational number
In this problem we find that the square root of 5 is equal to x + 3 and we need to find the exact value of the following algebraic expression:
y = (x + 3)², where x + 3 = √5.
Then, if we know that x + 3 = √5, then the exact value of y is:
y = (√5)²
y = 5
To learn more on square roots: https://brainly.com/question/1387049
#SPJ1
Help me please 4 questions 50 points this is due today




Answers
Answer:
Q15: A
Q12: A,C,D
Q13: B
Q14: C
Answer:
1) Left 5, Down 1
2) A, C, D
3) B
4) D
Step-by-step explanation:
Desmos graphing calculator will help you with all of these.
A batch of 1000 components of the same type for use in the Ash River neutrino detector is believed to include 5% which are faulty a) If 5 components are selected at random,what is the probability that no defective component will be chosen? b What is the probability that exactly 2 out of the 5 will be defective?
Answers
a) The probability that no defective component will be chosen when selecting 5 components at random is approximately 0.7738, or 77.38%.
b) The probability that exactly 2 out of the 5 components will be defective is approximately 0.0874, or 8.74%.
a) To calculate the probability that no defective component will be chosen when selecting 5 components at random, we need to determine the probability of selecting a non-defective component for each selection.
Since 5% of the components are faulty, the probability of selecting a non-defective component in each selection is 1 - 0.05 = 0.95.
The probability of selecting no defective components can be calculated using the multiplication rule for independent events. We multiply the probabilities of each selection being non-defective:
Probability of selecting no defective components = (0.95)⁵
Probability of selecting no defective components = 0.7738
b) To calculate the probability that exactly 2 out of the 5 components will be defective, we need to consider the different combinations of selecting 2 defective components out of 5.
The probability of selecting exactly 2 defective components can be calculated using the binomial probability formula:
Probability = (Number of ways to choose 2 defective components) * (Probability of selecting a defective component)^(Number of defective components) * (Probability of selecting a non-defective component)^(Number of non-defective components)
Probability = (5 choose 2) * (0.05)² * (0.95)³
Probability = (5! / (2! * (5-2)!)) * (0.05)² * (0.95)³
Probability = 0.0874
To learn more about probability click on,
https://brainly.com/question/32694665
#SPJ4
evaluate each expression for the given value of the variable-12/y ; y=3
Answers
Given the expression:
\(\text{ }\frac{-12}{y}\)At y = 3, it means that we substitute all the y variables in the expression into 3.
We get,
\(\text{ }\frac{-12}{y}\)\(\text{ = }\frac{-12}{3}\)\(\text{ = -4}\)Therefore, the answer is -4.
Can someone help me ASAP plz?

Answers
Answer:
D
Step-by-step explanation:
1 cm is 18 miles. if you have 14 cm you multiply 14 cm by 18 miles. you get 252 miles for 14 cm.
What is the value of (2/5)^3
Answers
The value of the exponent (2/5)^3 is \(\frac{8}{125}\)
In the above question, it is given that
(2/5)^3
The number of times a number has been multiplied by itself is referred to as an exponent. For instance, the expression 2 to the third (written as 2^3) signifies 2 x 2 x 2 = 8.
We need to solve it and then find the value of the exponent
(2/5)^3
= \(\frac{2}{5}\) x \(\frac{2}{5}\) x \(\frac{2}{5}\)
= \(\frac{2 . 2. 2}{5 . 5 . 5}\)
= \(\frac{8}{125}\)
Therefore the value of the exponent (2/5)^3 is \(\frac{8}{125}\)
To learn more about, exponential here
https://brainly.com/question/219134
#SPJ1
let be the set of the lowercase english letters and decimal digits. how many -strings of length satisfy all of the following properties (at the same time)? the first and last symbols of the string are distinct digits (which may appear elsewhere in the string). precisely four of the symbols in the string are the letter ''. precisely three characters in the string are elements of the set and these characters are all distinct.
Answers
The final answer is the sum of the number of possibilities for each case:
Total possibilities = Sum[(10 * 9 * (36)^n) * (nC4) * (36)^(n-4) * (36C3) * (nC3) * (36)^(n-3)] for all valid values of n.
To find the number of valid strings that satisfy the given properties, we can break down the problem into several cases and count the possibilities for each case.
Case 1: The first and last symbols are distinct digits.
There are 10 choices for the first digit (0-9) and 9 choices for the last digit (since it cannot be the same as the first digit). The middle characters can be any combination of letters and digits. Since there are no restrictions on the middle characters, we have a total of (36)^n possibilities, where n is the number of middle characters.
Case 2: Precisely four symbols in the string are the letter 'a'.
There are (nC4) ways to choose the positions of the four 'a' characters in the string, where n is the number of total characters in the string. For each arrangement of 'a's, the remaining characters can be any combination of letters and digits, which gives us (36)^(n-4) possibilities.
Case 3: Precisely three characters are elements of the set, and these characters are all distinct.
There are (36C3) ways to choose three distinct characters from the set of 36 (26 lowercase letters + 10 decimal digits). Once the three characters are chosen, they can be arranged in (nC3) positions in the string, where n is the total number of characters. The remaining characters can be any combination of letters and digits, which gives us (36)^(n-3) possibilities.
To find the total number of valid strings, we need to consider all possible combinations of these cases. Therefore, the final answer is the sum of the number of possibilities for each case:
Total possibilities = Sum[(10 * 9 * (36)^n) * (nC4) * (36)^(n-4) * (36C3) * (nC3) * (36)^(n-3)] for all valid values of n.
learn more about decimal digits here:
https://brainly.com/question/29196037
#SPJ11
solve for q.
5q + 2p + 4 = 3q – 8
Answers
Answer:
q = -p-6
Step-by-step explanation:
=> 5q+2p+4 = 3q-8
(Combining like terms)
=>5q-3q = -2p-8-4
=> 2q = -2p -12
=> 2q = 2(-p-6)
Dividing both sides by 2
=> q = -p-6
\(q = - p - 6\)
\(5q + 2p + 4 - 3q = - 8 \\ 2q + 2p + 4 = - 8 \\ 2q + 4 = - 8 - 2p \\ 2q = - 8 - 2p - 4 \\ 2q = - 12 - 2p \\ \frac{2q}{2} = \frac{ - 2p - 12}{2} \\ q = \frac{ - 2p - 12}{2} \\ q = - p - 6\)
in a random sample of six mobile devices, the mean repair cost was $75.00 and the standard deviation was $11.50. assume the population is normally distributed and use a t-distribution to find the margin of error and construct a 99% confidence interval for the population mean. interpret the results.
Answers
The margin of error is approximately $18.35, and the 99% confidence interval for the population mean repair cost is ($56.65, $93.35). This means we are 99% confident that the true population mean repair cost falls within this interval.
To calculate the margin of error, we use the formula: Margin of Error = t × (standard deviation / √n), where t is the critical value for the desired confidence level, standard deviation is the sample standard deviation, and n is the sample size.
With a sample mean repair cost of $75.00 and a standard deviation of $11.50, and a sample size of 6, we need to determine the critical value associated with a 99% confidence level. Since the sample size is small (n < 30), we use a t-distribution instead of a z-distribution.
Using the t-distribution with (n-1) degrees of freedom, where n is the sample size, and a confidence level of 99%, we find the critical value to be approximately 3.707.
Next, we calculate the margin of error: Margin of Error = 3.707 × (11.50 / √6) ≈ 18.35.
To construct the 99% confidence interval, we take the sample mean and add/subtract the margin of error: 75.00 ± 18.35. This gives us a confidence interval of approximately (56.65, 93.35).
learn more about z-distribution here:
https://brainly.com/question/28977315
#SPJ11
Which of the following is a function?

Answers
Answer:
i think the last one
Step-by-step explanation:
a 1 =−4a, start subscript, 1, end subscript, equals, minus, 4 a_i = a_{i - 1} \cdot 2a i =a i−1 ⋅2
Answers
The given equation is a recursive formula where a subscript i equals the product of a subscript i-1 and 2, with the initial value of a subscript 1 being -4a.
The equation represents a recursive relationship between the terms of the sequence. Starting with the initial term, a subscript 1, the subsequent terms are determined by multiplying the previous term, a subscript i-1, by 2. This recursive formula can be written as a subscript i = a subscript i-1 * 2.
Given that a subscript 1 = -4a, we can use this initial value to find the subsequent terms of the sequence. To calculate a subscript 2, we substitute i = 2 into the formula:
a subscript 2 = a subscript 2-1 * 2 = a subscript 1 * 2 = -4a * 2 = -8a.
Similarly, for a subscript 3:
a subscript 3 = a subscript 3-1 * 2 = a subscript 2 * 2 = -8a * 2 = -16a.
By applying the recursive formula repeatedly, we can generate the terms of the sequence. Each term is obtained by multiplying the previous term by 2.
Learn more about recursive formula here:
https://brainly.com/question/1470853
#SPJ11
How many solutions does the equation 3(4h−1)=−4(3h−5) have?
Answers
Answer:
Step-by-step explanation:
I don’t want more question
I need help no more stress????
If x-1 over 3 = k and k=3, what is the value of x ?
Answers
\(x = 10\)
Step-by-step explanation:Given:
\(\frac{x -1}{3} = k \text{ where } k = 3\)
Solving for \(x\):
\(\frac{x -1}{3} = k \text{ where } k = 3\\ \frac{x -1}{3} = 3 \\ \frac{x -1}{3} \cdot 3 = 3 \cdot 3 \\ x -1 = 9 \\ x -1 +1 = 9 +1 \\ x = 10\)
\( \large \frac{x - 1}{3} = k \: and \:k = 3 \)
__________________________________________
\(\large\bf{\underline{Putting\: the\:value\:of\:k}}\)
\(⟹ \large \frac{x - 1}{3} = 3\)
\(⟹\large {x - 1 = 3 \times 3}\)
\(⟹\large{x = 9 + 1}\)
\(⟹\large{x = 10}\)
__________________________________________
\(\large\bf{\underline{Hence}}\)
\(\huge{⟹x = 10}\)
NO LINKS PLEASE the question and answer is below
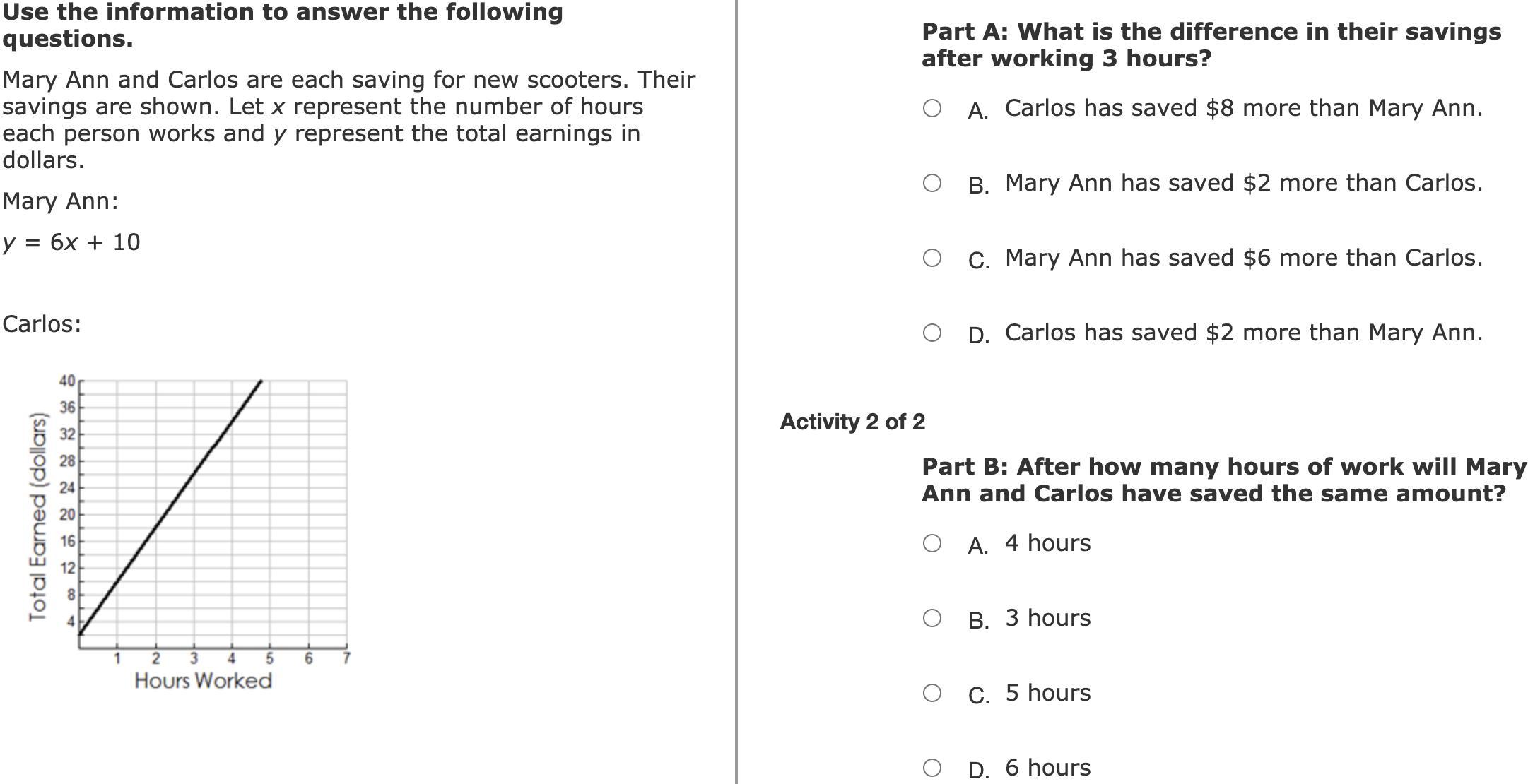
Answers
Second answer is A
THE NUMBER 1-10 ARE IN A BAG, YOU TAKE 2 OUT WITHOUT REPLACEMENT. WHAT IS THE PROBABILITY OF DRAWING THE NUMBER 7 THE FIRST TIME AND THEN DRAWING AN EVEN NUMBER.
Answers
Answer:
1 / 18
Step-by-step explanation:
PROBABILITY OF DRAWING THE NUMBER 7 THE FIRST TIME = Number of favorable outcome / Total number of outcomes
Favorable outcome = 1
Total number of outcome (1,2,3,4,5,6,7,8,9,10) = 10
PROBABILITY OF DRAWING THE NUMBER 7 THE FIRST TIME = 1 / 10
PROBABILITY OF DRAWING AN EVEN NUMBER THE SECOND TIME = Number of favorable outcome / Total number of outcomes
Favorable outcome (2,4,6,8,10) = 5
Total number of outcomes (1,2,3,4,5,6,8,9,10) = 9
PROBABILITY OF DRAWING AN EVEN NUMBER THE SECOND TIME = 5/9
PROBABILITY OF DRAWING THE NUMBER 7 THE FIRST TIME AND THEN DRAWING AN EVEN NUMBER = 1 / 10 * 5 / 9 = 1 / 18
