Answers
The angle becomes:
∠A = 70.306°
∠B = 73.381°
∠C = 73.381°
What is an angle?The Latin word "angulus," which meaning "corner," is where the term "angle" comes from. The common terminus of two rays is known as the vertex, and the two rays are known as sides of an angle. A triangle has three angles. The triangle's two sides meet at the triangle's vertices to produce these angles. The total of the three inner angles is 180 degrees.
Triangle types based on the angles, these are:
Acute-angled.Obtuse-angled.Right-angled.Given that for the given triangle:
a = 4
b = 7
c = 7
Next, ∠A = cos⁻¹(b² + c² - a²/2bc)
∠A = cos⁻¹ [(7)² + (7)² - (4)²/2(7×7)]
∠A = cos⁻¹ (0.337)
∠A = 70.306°
Next,
∠B = cos⁻¹(a² + c² - b²/2ac)
∠B = cos⁻¹ [(4² + 7² - 7²/2(7×4)]
∠B = cos⁻¹ (0.286)
∠B = 73.381°
Next,
∠C = cos⁻¹(a² + b² - c²/2ab)
∠C = cos⁻¹ [4² + 7² - 7²/2(7×4)]
∠C= cos⁻¹ (0.286)
∠C = 73.381°
To know more about angle refer to:
https://brainly.com/question/28144202
#SPJ1
Related Questions
What is the equation to 6x=0.4
Answers
Answer:
Step-by-step explanation:
15
The coordinates of point A on a grld are (-3,-2), Point A is reflected across the y-axls to obtain point B. The coordinates of point B are
-2).
Answers
Answer:
The coordinates of the image of B(-3, -2) is B'(3, -2).
Step-by-step explanation:
We know that when a point (x, y) is reflected across the y-axis, the y-coordinate remains the same, and then the x-coordinate becomes negative.i.e.
Thus, the image of P(x, y) is P' (-x, y).Given the point
B(-3, -2)Hence, the image of B(-3, -2):
(-x, y) → (-(-3), -2) = (3, -2)Therefore, the coordinates of the image of B(-3, -2) is B'(3, -2).
mathmatically indication example with solution
Answers
A mathematically indication example would be to solve the equation 3x + 2 = 14 for the value of x. The solution would be 4.
How to solve the equation ?Looking for a mathematically indication example, we can consider a simple mathematical equation with one variable and solve it.
The equation would be 3 x + 2 = 14.
So we can solve for the equation to be :
3x + 2 - 2 = 14 - 2
3x = 12
3 x / 3 = 12 / 3
x = 4
In conclusion, the mathematically indication example would be 3x + 2 = 14 and the value of x would be 4.
Find out more on equation solutions at https://brainly.com/question/2228446
#SPJ1
Please help me please help no links

Answers
What is the right-hand limit of the function f(x)=x^2+2x−3/x−1 as x approaches 2?
Answers
The right-hand limit of f(x) as x approaches 2 is 5.
To find the right-hand limit of the function f(x) as x approaches 2, we need to evaluate the function as x approaches 2 from the right-hand side (i.e., values of x greater than 2).
So, let's first rewrite the function:
\(f(x) = (x^2 + 2x - 3)/(x - 1)\)
Now, we can substitute x = 2 + h, where h is a small positive number, since we want to approach 2 from the right-hand side.
\(f(2 + h) = [(2 + h)^2 + 2(2 + h) - 3]/(2 + h - 1)\\= [(4 + 4h + h^2) + 4 + 2h - 3]/(1 + h)\\= (h^2 + 6h + 5)/(1 + h)\)
Now, we can evaluate the limit as h approaches 0 from the right-hand side:
lim (h→0+) f(2 + h) = lim (h→0+) \((h^2 + 6h + 5)/(1 + h)\)
= \([(0)^2 + 6(0) + 5]/(1 + 0)\)
= 5
for such more question on right-hand limit
https://brainly.com/question/12017456
#SPJ11
1. 18x^3-2x^2+4x-1
1.1 How many terms are in 18x^3-2x^2+4x-1
Answers
The polynomial 18x³ - 2x² + 4x - 1 consists of four terms.
The number of terms in a polynomial helps when performing operations like simplification, factoring, or evaluating expressions.
The polynomial 18x³ - 2x² + 4x - 1 consists of four terms.
In order to determine the number of terms in a polynomial, we count the number of distinct algebraic expressions separated by addition or subtraction operations.
In this polynomial, we have:
Term 1: 18x³ (This is the term with the highest degree, which is 3 in this case, and it includes the coefficient 18.)
Term 2: -2x² (This term has a degree of 2 and a coefficient of -2.)
Term 3: 4x (This term has a degree of 1 and a coefficient of 4.)
Term 4: -1 (This is a constant term with a degree of 0.)
We can see that there are four distinct terms separated by addition and subtraction operations:
18x³, -2x², 4x, and -1.
For similar questions on polynomial
https://brainly.com/question/12702996
#SPJ8
..................................
Answers
MADE BY FACEESLASHA
DIGITEL ANGELS, ANGELS, A-A-ANGELS
How does hardware differ from software?
Hardware can be an external tool, whereas software is an internal tool.
Hardware performs tasks, whereas software provides instructions.
Hardware runs the computer, whereas software performs tasks.
Hardware is the brain of a computer, whereas software is the heart.
those fools playing you its actually: B. Hardware performs task, whereas software provides instructions.
Answers
Answer:
B
Step-by-step explanation:
answer in question lol
Answer:
it could be A or B but B seems more correct.
BRAINLIEST to whoever shows work the best

Answers
Answer: The value of x is 9.
Step-by-step explanation: n a regular hexagon, all interior angles have the same measure.
Since a hexagon has six sides, the sum of its interior angles is given by the formula:
Sum of interior angles = (6 - 2) × 180° = 4 × 180° = 720°
Since all interior angles of a regular hexagon have the same measure, we can find the measure of each angle by dividing the sum by the number of angles:
Measure of each angle = Sum of interior angles / Number of angles = 720° / 6 = 120°
We are given that one of the angles in the hexagon is (11x + 21)°. Setting this equal to 120° and solving for x, we get:
11x + 21 = 120
11x = 99
x = 9
Therefore, the value of x is 9.
Pls help I’m failing math I’ll brainlest for the right answer grades close today

Answers
answer: i think that it would increase by about 20 percent
i am not sure, if i m wrong then i am very sorry!
Step-by-step explanation:
Answer:
The change is a decrease by ~13.6%
Step-by-step explanation:
Formula:
[First Value – Second Value] ÷ [(First Value + Second Value) ÷ 2] × 100
48 - 84 ÷ 48 + 84 ÷ 2 × 100
-36 ÷ 132 ÷ 2 × 100
-0.2727272727272727 ÷ 2 × 100
-0.1363636363636364 × 100
-13.63636363636364
Or ~ 13.6
The change is a decrease by ~13.6%
give me the answer for the problem

Answers
Answer:
\(-8x^3\sqrt{7}\)
Step-by-step explanation:
Step 1: Let's start by simplifying -4x^2 * (√63x^2) using the following steps:
1.1: Separate √63x^2 into two terms:
-4x^2 * (√63 * √x^2)
1.2: Find the largest perfect square that we can factor out of 63. It's 9 as 3^2 = 9 and 9 * 7 = 63. Furthermore, √x^2 simplifies to x:
-4x^2 * (√9 * 7 * (x))
-4x^2 * (3√7 * x)
1.3: We can multiply x and 3:
-4x^2 * (3x√7)
1.4: We can distribute -4x^2 to 3x√7.
Multiplying the coefficients will give us -12 as -4 * 3 = 12.x^2 * x = x^3-12x^3 * √7
Step 2: Now we can work on simplifying x^3√112 using the following steps:
2.1: Find the largest perfect square you can factor out of 112. It's 16 since 4^2 = 16 and 16 * 7 = 112:
x^3 * √16 * 7
x^3 * 4√7
2.2: Multiply x^3 and 4√7:
4x^3 * √7
Step 3: Thus, -4x^2 * √63x^2 simplified individually is -12x^3 * √7 and x^3 * √112 simplified individually is 4x^3 * √7
3.1: Add -12x^3 * √7 + 4x^3 * √7:
-8x^3√7
Optional Step 4: We can check that we've correctly simplifed the equation by plugging in a number for x in both the radical expression not yet simplified and the simplified radical expression. If we get the same answer, then we've simplified the expression correctly. We can plug in 2 for x.
Plugging in 2 for x in -4x^2 * (√63x^2) + x^3 * (√112):
(1.) -4(2)^2 * √63(2)^2 + 2^3 * √112:
(2.) -4(4) * √63(4) + 8 * √112
(3.) -16 * √252 + 8 * √112
(4.) -16 * √36 * 7 + 8 *√16 * 7
(5.) -16 (6 * √7) + 8(4 *√7)
(6.) -96 * √7 + 32 * √7
(7.) -64√7
(8.) -169.3280839
Plugging in 2 for x in -8x^3√7:
(1.) -8(2)^3 * √7
(2.) -8(8) * √7
(3.) -64 * √7
(4.) -169.3280839
Therefore, we've correctly expressed the expression in simplest radical form
Can someone please please help me!!

Answers
Answer:
c
Step-by-step explanation:
Find the quotient of z₁ by z2. Express your answer in
trigonometric
form.
² - 3 (0 (4) + (*))
Z₁ cos
+/sin
Z₂
²2 = 7 (cos(377)+
COS
8
O A. 7 (cos (577) + i sin (5/77))
8
B.
21(cos(577)+isin (577))
8
OC. 21 cos
21(cos(-7)+ i sin(-77))
O D. 7 (cos(-7) + + sin(-7))
i
+/sin
37T
8

Answers
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
To find the quotient of z₁ by z₂ in trigonometric form, we'll express both complex numbers in trigonometric form and then divide them.
Let's represent z₁ in trigonometric form as z₁ = r₁(cosθ₁ + isinθ₁), where r₁ is the magnitude of z₁ and θ₁ is the argument of z₁.
We have:
z₁ = 7(cos(577°) + i sin(577°))
Now, let's represent z₂ in trigonometric form as z₂ = r₂(cosθ₂ + isinθ₂), where r₂ is the magnitude of z₂ and θ₂ is the argument of z₂.
From the given information, we have:
z₂ = 21(cos(-7°) + i sin(-77°))
To find the quotient, we divide z₁ by z₂:
z₁ / z₂ = (r₁/r₂) * [cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)]
Substituting the given values, we have:
z₁ / z₂ = (7/21) * [cos(577° - (-7°)) + i sin(577° - (-7°))]
= (7/21) * [cos(584°) + i sin(584°)]
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
Option C, 21(cos(-7°) + i sin(-77°)), is not the correct answer as it does not represent the quotient of z₁ by z₂.
For more questions on trigonometric form
https://brainly.com/question/31744474
#SPJ8
When I think of a number, double it, then add
seven, I get 23. Determine the number that I
first thought of.
Answers
Answer:
8
Step-by-step explanation:
23 - 7
= 16
16 ÷ 2
= 8
u thought of 8 ;)
Answer:
number maybe 8...
Step-by-step explanation:
because if you will double 8 then you will get 16 and if you will add 16 with 7 you will get 23....
Ms. Dawson's call did a science experiment. The class started out with 635 bacteria cells. The growth rate
predicted was 5.15%. Sketch the graph that represents the situation. Label the y-intercept and the point that
represents the projected bacteria population 23 h from the start of the experiment. Be sure to show your work
on how you obtained your second value. Round to the nearest whole number.
Answers
The exponential function obtained from the table is represented by the formula y is 650(1.045)x.
Exponential operation?A function with the exponential shape is:
y = abˣ
where an is y's initial value, b are multipliers, and y and x are variables.
The bacterial population at x hours should be represented by y.
With 650 bacteria cells at the beginning, the group.
a = 650
4.5% is the growth rate.
b = 100% + 4.5% = 104.5% = 1.045
The exponential function obtained from the table is represented by the formula y = 650(1.045)x.
The exponential function obtained from the table is represented by the formula y is 650(1.045)x.
Thirty hours later:
y = 650(1.045)³⁰ = 2434.
To learn more about the exponential function refer to brainly.com/question/12940982
#SPJ1
Vector u = <2, -5>. Describe how you would use a graphical method to add vector u to vector v (3, 1). Then, write the resultant vector in component form.
Answers
The component form of the resultant vector is <5, -4>
How to describe the use of graphical method for adding vectors?Let vector u be a displacement AB on the graph and let vector v be a displacement BC on the graph such that the sum of displacement AB and BC is equivalent to a single displacement AC on the graph. We can write this as:
AB + BC = AC
or writing the vector sum with small letters given,
u + v = w (Note: w = AC)
Given: vector u = <2, -5> and vector v (3, 1)
u + v = w
<2, -5> + <3, 1> = <2+3, -5+1> = <5, -4>
u + v = <5, -4>
Thus, the coordinates of the vector sum on the graph will be (5, -4)
Therefore, the resultant vector in component form is <5, -4>
Learn more about vector on:
https://brainly.com/question/25705666
#SPJ1
A rectangular prism with a square base has a height of 17.2cm and a volume of 24.768cm². What is the length of its base?
Answers
The formula for the volume of a rectangular prism is:
V = lwh
where V is the volume, l is the length, w is the width, and h is the height.
We know that the height of the rectangular prism is 17.2 cm, and the volume is 24.768 cm³. We also know that the base is a square, so the length and width are the same. Let's call the length of the base x.
Then, we can write:
V = lwh
24.768 = x * x * 17.2
24.768 = 17.2x²
x² = 1.44
x = 1.2
Therefore, the length of the base of the rectangular prism is 1.2 cm.
The formula for the volume of a rectangular prism is V = lwh, where l is the length, w is the width, and h is the height.
In this problem, we know that the height is 17.2 cm, and the volume is 24.768 cm³. We also know that the base is a square, so the length and width are the same.
Therefore, we can write the equation:
24.768 = x² * 17.2
To solve for x, we can divide both sides by 17.2, and then take the square root of both sides:
x² = 24.768 / 17.2
x² = 1.44
x = sqrt(1.44)
x = 1.2
Therefore, the length of the base of the rectangular prism is 1.2 cm.
Negative values pertain to ounces under 16. Find the probability that a box of cereal will be: a.more than one ounce underweight. b. neither underweight a. nor more than 1 ounce overweight. tly 16 ounces. C. exactly 16 ounces
Answers
Probability is simply how likely something is to happen. There can be many probability of the same thing to occur in future. the probability that a box of cereal will be:
A. The probability that a box of cereal will be more than one ounce underweight is equivalent to the probability of getting a weight less than 15 ounces. Using a standard normal distribution table or calculator, we can find that this probability is approximately 0.0228 or 2.28%.
B. The probability that a box of cereal will not be underweight is equivalent to the probability of getting a weight greater than or equal to 16 ounces. Using a standard normal distribution table or calculator, we can find that this probability is approximately 0.5 or 50%.
C. The likelihood that a package of cereal will weigh less than or equal to 17 ounces is the same as the likelihood that it won't be more than 1 ounce overweight. This chance can be calculated using a typical normal distribution chart or calculator as 0.9772 or 97.72%.
D. Because weight is a continuous variable with an infinitesimally tiny chance of attaining any precise value, the likelihood of receiving exactly 16 ounces is very low. The area under the normal distribution curve between 15.5 and 16.5 ounces, or roughly 0.3829 or 38.29%, can be used to determine the chance.
Possibility or probability is all game of occurrence of the thing.
To know more about Probability-
brainly.com/question/29381779
#SPJ4
A cellular phone company monitors monthly phone usage. The following data represent the monthly phone use in minutes of one particular
customer for the past 20 months. Use the given data to answer parts (a) and (b).
325 517 424 395 494
396 351 379 408 426
523 421 434 373 456
535 394 437 403 513
(a) Determine the standard deviation and interquartile range of the data.
s=(Round to two decimal places as needed.)
Answers
Answer:
The answer is: 325 517 424 395 494
Step-by-step explanation:
Dividing by a Monomial
What is (9x^3-6x^2+15x) ÷ 3x^2?
Answers
Answer:
\(3x-2+\frac{5}{x}\)
Step-by-step explanation:
To divide the polynomial (9x^3 - 6x^2 + 15x) by the monomial 3x^2, we can write it as:
(9x^3 - 6x^2 + 15x) ÷ (3x^2)
To simplify the division, we divide each term of the polynomial by 3x^2:
(9x^3 ÷ 3x^2) - (6x^2 ÷ 3x^2) + (15x ÷ 3x^2)
To divide monomials with the same base, we subtract the exponents. So:
9x^3 ÷ 3x^2 = 9/3 * (x^3/x^2) = 3x^(3-2) = 3x
(-6x^2) ÷ (3x^2) = -6/3 * (x^2/x^2) = -2
15x ÷ 3x^2 = 15/3 * (x/x^2) = 5/x
Putting it all together, we have:
(9x^3 - 6x^2 + 15x) ÷ (3x^2) = 3x - 2 + 5/x
Therefore, the division of (9x^3 - 6x^2 + 15x) by 3x^2 is 3x - 2 + 5/x.
arccsc(\(\frac{2}{3}\)\(\sqrt{3}\))
Answers
The arc cossecant of the given value is of 30º.
Cosecant and arc cosecantThe cosecant of an angle is given by the ratio between 1 and the sine of the angle, as follows:
cos(x) = 1/sin(x)
The arc cossecant of an angle is represented by the expression arc csc(x), and represents the inverse of the cossecant, that is, it is the angle which has a cosecant of x.
In this problem, the arc cossecant that is asked is:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)}\)
Basically, it asks for the angle which has a cossecant value of 2/(3sqrt(3)). This angle is found using a calculator, and it is of 30º.
Hence the numeric value of the expression is presented as follows:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)} = 30^\circ\)
More can be learned about cossecant and arc cossecant at https://brainly.com/question/13276558
#SPJ1
I need the answers for the table below.

Answers
The values of f(x) for the given x - values rounded to 4 decimal places are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013 respectively
Given the function :
tan(πx)/7xSubstitute the given value of x to obtain the corresponding f(x) values :
x = -0.6
f(x) = (tanπ(-0.6))/7(-0.6) = 0.0078358
x = -0.51
f(x) = (tanπ(-0.51))/7(-0.51) = 0.0078350
x = -0.501
f(x) = (tanπ(-0.501))/7(-0.501) = 0.001967
x = -0.5
f(x) = (tanπ(-0.5))/7(-0.5) = 0.001959
x = -0.4999
f(x) = (tanπ(-0.4999))/7(-0.4999) = 0.001958
x = 0.499
f(x) = (tanπ(-0.499))/7(-0.499) = 0.001951
x = -0.49
f(x) = (tanπ(-0.49))/7(-0.49) = 0.00188
x = -0.4
f(x) = (tanπ(-0.4))/7(-0.4) = 0.00125
Therefore, values which complete the table are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013
Learn more on functions : https://brainly.com/question/12634120
#SPJ1
We expect that students who do well on the midterm exam in a course will usually also do well on the final exam. Gary Smith of Pomona College looked at the exam scores of all 346 students who took his statistics class over a 10-year period. The least-squares line for predicting final-exam score from mid-term exam score was γ=46.6 + 0.41x.
Octavio scores 10 points above the clas mean on the midterm. How many points above the class mean do you predict that he will score on the final. (Hint: what is the predicted final-exam score for the class mean midterm score of x-bar?) This is an example of regression to the mean, the phenomenon that gave "regression" its name: students who do well on the midterm will on average do less well on the final, but still above the class mean.)
Answers
Using the model equation, the predicted mean score on the final given a score of 10 points above the class mean in the mid term exam is 50.7
The Least - Square Regression equation which models the relationship between midterm and final exam score is :
γ=46.6 + 0.41xx = 10 points ; substitute the value of x = 10 into the regression equation ;
γ=46.6 + 0.41(10)
γ=46.6 + 4.1
γ = 50.7
The number of points above the mean he'll score in the final exam is predicted to be 50.7
Learn more :https://brainly.com/question/18405415
HELP PLEASEEE !!! 50 POINTS

Answers
Answer:
haha
Step-by-step explanation:
first off thats not 50 points
Answer:
Step-by-step explanation For the first on 5 and -4 all u do is divide y over x so it wpuld be -4/5 which would be -0.8
just keep doing the process of dividing y over x
the second 1 would be 0/3 which is 0
just keep doing this process
if the dilation of K(-2,4) equals K'(1,-2), the scale factor used for the dilation is
Answers
Answer:
-1/2
Step-by-step explanation:
We know
The dilation of K(-2,4) equals K'(1,-2)
To get from -2 to 1, we time -1/2
To get from 4 to -2, we time -1/2
So, the scale factor used for the dilation is -1/2
The formula a² + b²>² is used to show that a triangle with sides a,
b, and c is an acute triangle. Which shows this formula solved for b?
A b>c-a
B b> c²-a
C b> √c-a
D b>√c²-a²
Answers
The expression that shows the formula solved for b is option D. b>√c²- a².
Relationship among the sides of an acute triangle.
There are different types of triangle in which acute triangle is one. An acute triangle is a type of triangle in which the measure of all its internal angles is less than a right angle. So that the length of its three sides are related by the formula:
a² + b² > c²
To show this formula solved for b, make b the subject of formula,
b² > c² - a²
Then find the square root of both sides of the expression to have,
b >√c²- a²
This shows the formula solved for b in terms of a and c.
Therefore, the expression that shows the formula for b in the given question is option D. b > √c²- a²
Learn more about the relations among the sides of an acute triangle at https://brainly.com/question/4578584
#SPJ1
Find the length of the hypotenuse. Round your answer to the nearest tenth if necessary.
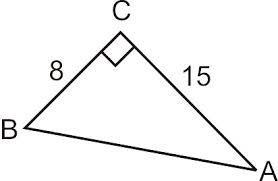
Answers
Answer:
a^2 + b^2 = c^2
8^2 + 15^2 = c^2
64 + 225 = c^2
289 = c^2
17 = c
The hypotenuse is 17.
Brainliest? ;)
Which graph is a parabola?

Answers
Answer:
The third one from the left
Step-by-step explanation:

What is the maximum of f(x)=sin(x)
Answers
Answer:
1
Step-by-step explanation:
The maximum of f(x) = sin(x) is 1. The sine function has a range of -1 ≤ sin(x) ≤ 1. The sine function oscillates between -1 and 1, reaching a maximum of 1 when x = π/2 and a minimum of -1 when x = -π/2. If you look at a graph of
y = sin(x) you can see this.
Answer: The Maximum Value of f(x)=sin(x) is 1 , when x=90°.
Step-by-step explanation:
Property of Sine function:
Sin(x)=0 when x=90°,180°,360°The maximum and Minimum value of Sin(x) is 1 and -1 respectively, when and x=270° respectively.The range of values of sin(x) is -1 to 1.Read more on the Sine function:
https://brainly.com/question/21902442
https://brainly.com/question/29529184
https://brainly.com/question/23214084
I need help solving please
Answers
It is given that there is deck of cards
There are 52 cards.
Among them there are 4 cards which are numbered 5.
Hence in first draw, the number posibilities is 4.
Hence the probability is
\(\frac{4}{52}\)Similarly in the second draw the number of possibilites is 4 since the card is replaced.
Hence the probability is
\(\frac{4}{52}\)Hence for five draws, the probability is
\(\frac{20}{52}=\frac{5}{13}\)