PLEASE HELP ME ASAP?!?
Find the length of the missing side. Simplify all radicals.

Answers
Answer:
22.47
22.5 (simplified)
Step-by-step explanation:
22.47 = √(8^2 + 21^2)
Related Questions
Let S represent the number of randomly selected adults in a community surveyed to find someone with a certain genetic trait.
The random variable S
follows a geometric distribution with mean 4.66. Which of the following is a correct interpretation of the mean?
A. A value randomly selected from the distribution of S
is expected to be 4.66.
A value randomly selected from the distribution of S is expected to be 4.66.
B. In repeated sampling from the distribution of S
, the average of the values will approach 4.66.
In repeated sampling from the distribution of S, the average of the values will approach 4.66.
C. For a sample of values randomly selected from the distribution of S
, the average of the sample will be 4.66.
For a sample of values randomly selected from the distribution of S, the average of the sample will be 4.66.
D. The probability is 0.66 that a value randomly selected from the distribution of S
will be close to the mean.
The probability is 0.66 that a value randomly selected from the distribution of S will be close to the mean.
E. For a sample of values randomly selected from the distribution of S
, the average of the sample will vary from the population mean by no more than 4.66.
Answers
Answer:
In repeated sampling from the distribution of S , the average of the values will approach 4.66.
Step-by-step explanation:
The correct interpretation of the mean is in repeated sampling from the distribution of S, the average of the values will approach 4.66.
The Geometric distribution is a discrete probability distribution that shows the likelihood of the number of failures before the success attained.
Let consider S to be a random variable that represents the selected adults in a community surveyed.
Then
\(\mathbf{S \sim G(p) S = 4.66}\)
Therefore, the correct interpretation of the mean is in repeated sampling from the distribution of S, the average of the values will approach 4.66.
Learn more about Geometric distribution here:
https://brainly.com/question/3216901?referrer=searchResults
The probability of a unit falling below the LSL and the probability of a unit being above the USL is the same when the ____ of the distribution is in the middle of the tolerance interval.
Answers
The probability of a unit falling below the Lower Specification Limit (LSL) and the probability of a unit being above the Upper Specification Limit (USL) is the same when the mean of the distribution is in the middle of the tolerance interval.
In a manufacturing or quality control context, a tolerance interval represents the acceptable range of values for a certain characteristic of a product. The Lower Specification Limit (LSL) defines the lower end of the acceptable range, while the Upper Specification Limit (USL) defines the upper end.
When the mean of the distribution is in the middle of the tolerance interval, it implies that the distribution is symmetric and centered within the tolerance limits. In this scenario, the distribution is balanced around the mean, and the probability of a unit falling below the LSL is equal to the probability of a unit being above the USL.
This equality in probabilities occurs because the distribution is equally distributed on both sides of the mean. As a result, the proportion of units falling below the LSL is the same as the proportion of units exceeding the USL. This balance indicates that the process is centered within the tolerance limits, which is desirable in manufacturing to ensure that both underperforming and overperforming units are equally unlikely.
Learn more about probability here;
https://brainly.com/question/31828911
#SPJ11
please help me!! i’ll mark brainliest if you’re correct <3
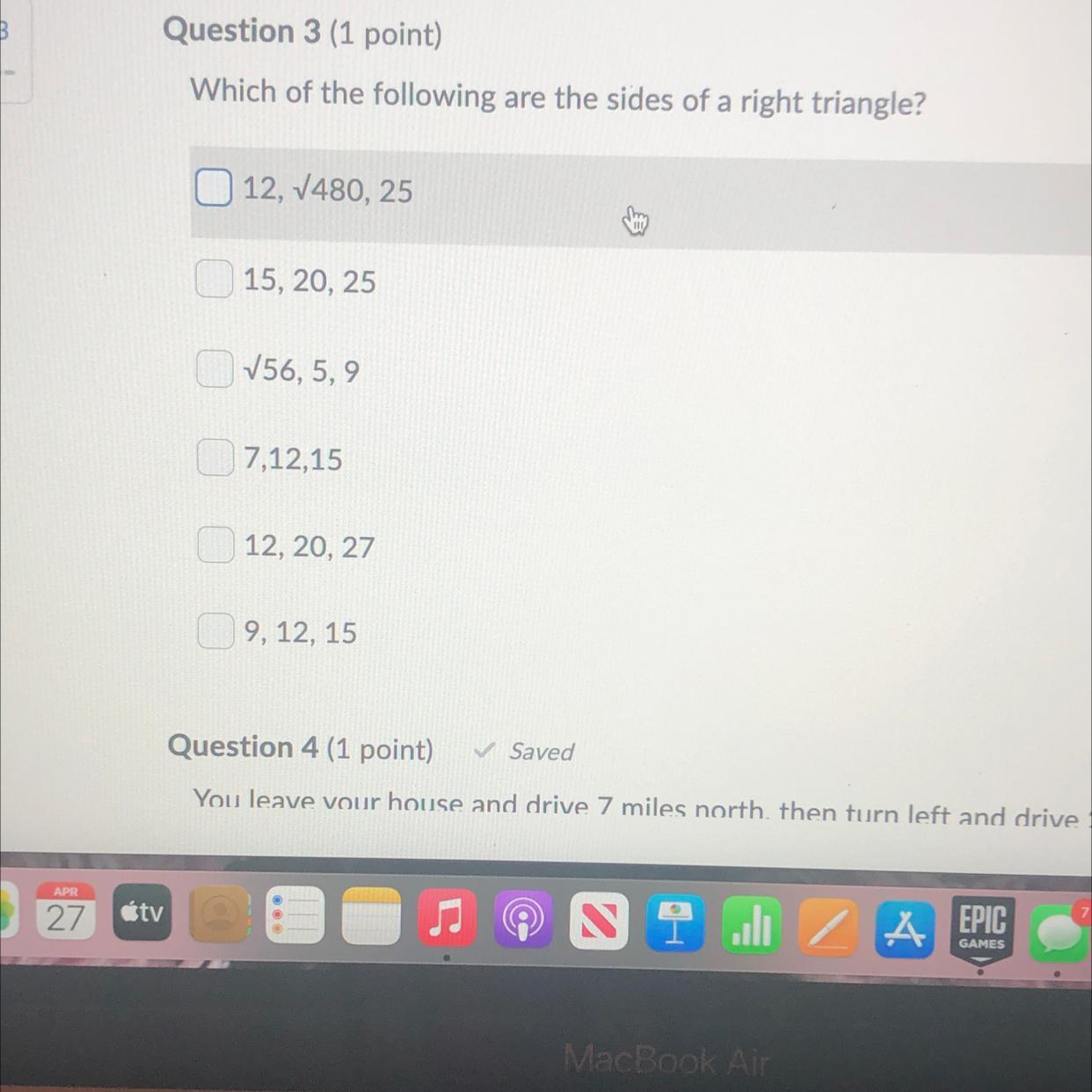
Answers
Answer:
9, 12,15
Step-by-step explanation:
a^2+b^2=c^2
9^2+12^2=15^2
81+144=225
If h(x)=x-7and g(x)=x^2, which expression is equivalent to(g*h)(5)?
Answers
Answer:
(g*h)(5) is g(h)=x
Step-by-step explanation:
because if h(x)=x-7 and g(x)=x^2.
help meeeee this are the last of my mf pointssssss

Answers
Answer:
y=0.6 x=3.6
dddddddddddddddddd
what is 55 percent of 110
Answers
Answer:
60.5
Step-by-step explanation:
Select the correct answer.
A principal amount of $15,340 is deposited into an account paying interest at a rate of 5%, continuously compounded. What will the account balance be after 7 years?
Answers
The account balance will be approximately $21,796.29 after 7 years.
The formula for continuous compounding is given by
\(A = Pe^{rt}\)
where A is the ending account balance, P is the principal amount, r is the annual interest rate as a decimal, t is the time in years, and e is the mathematical constant approximately equal to 2.71828.
In this problem, the principal amount is $15,340, the annual interest rate is 5%, and the time is 7 years. We can substitute these values into the formula to find the ending account balance
\(A = 15340e^{0.057}\)
Simplifying
\(A = 15340*e^{0.35}\)
A = 15,340 * 1.4187
A = $21,796.29
Therefore, the correct answer is (c) $21,796.29.
To know more about account balance:
https://brainly.com/question/28699225
#SPJ1
The algebraic expression p(x) = 3x^4 +1 can become a polynomial:
a) for any value of a, b and c
b) a + b=c
c) b=0
d) b=√2
Answers
Answer:
A polynomial p(x) in one variable x is a mathematical articulation in x of the structure p(x) = anx n + an−1x n−1 + ....... + a2x 2 + a1 x + a0, where a0, a1, a2, .... an are individually the coefficients of x 0 , x 1 , x 2 , .... x n and n is known as the level of the polynomial if a ≠ 0. Each anx n ; an−1x n−1 ; .... a0, is known as a term of the polynomial p(x)
14. Find the area under the normal curve to the right of z = 1.84.
A. 0.9671
B. 0.0329
C. 0.2005
D. 0.7995
Answers
Answer:
B is the correct answer from my understanding
Step-by-step explanation:
What is the standard form of this expression?
(4y − 9)(2y − 3)
Answers
PLS HELP ME ;;;-;;;
I have the answer all I need is to show the work so pls help me with that
Find the value of X.

Answers
Answer:
X=11
Step-by-step explanation:
9x+6= (3x+2)+(70)
Simplify: 6x+6=72
6x+6=72
6x=66
x=11
Evaluate the expression 3 • 5x when x is 2.

Answers
3 • 125 = 375
375 is your answer
Answer: 3 ⋅ \(5^2\) = 75
Step-by-step explanation:
3⋅\(5^2\)
3⋅25
75
Does anyone know this answer
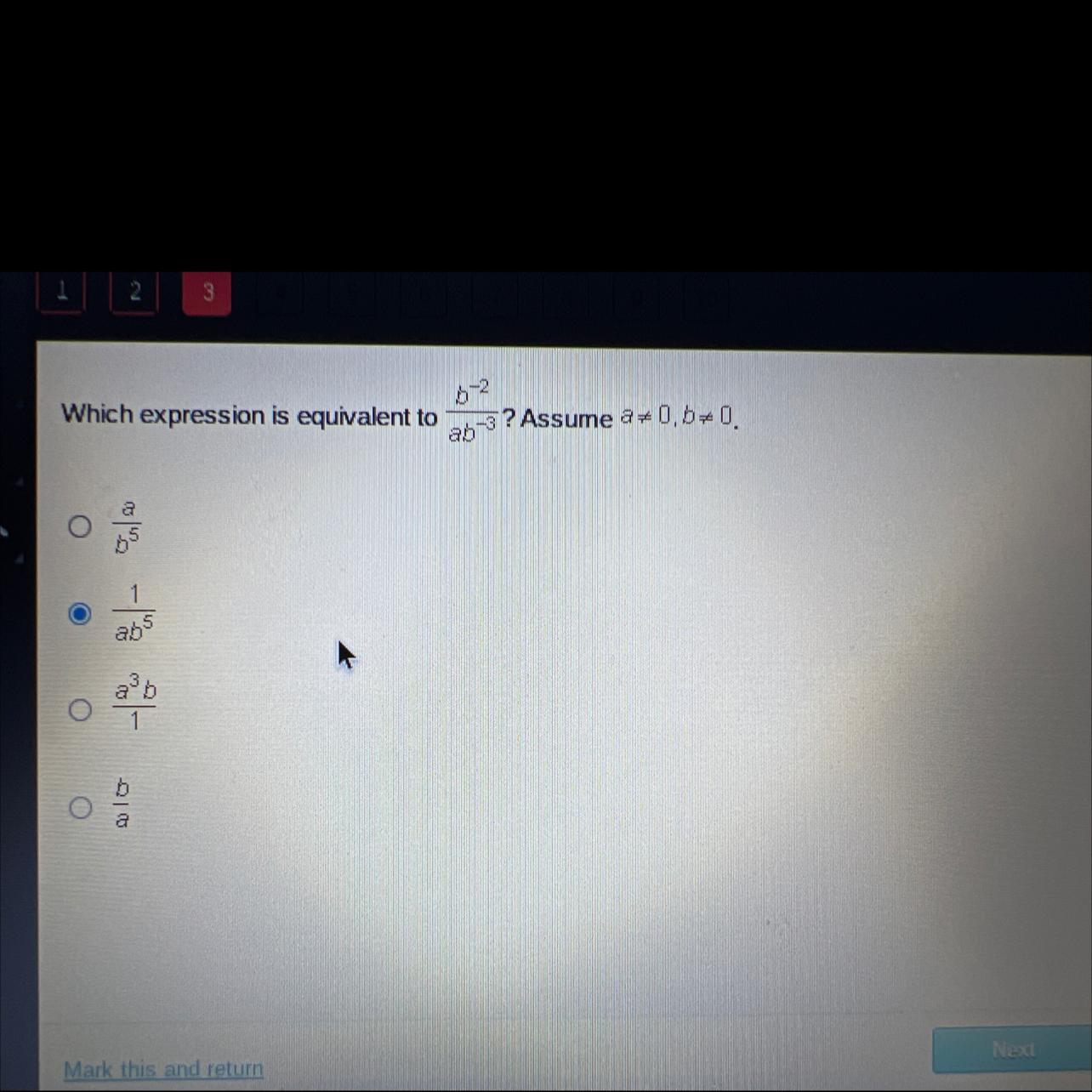
Answers
The length of my outdoor volleyball net is 6 m plus half its own length. How long is the net?
Answers
Answer:
12 meters
Step-by-step explanation:
The length of the volleyball net is "L"
6 + 1/2 L = L <======this is given , solve for L
6 = 1/2 L
L = 12 Meters
a normalized binary number consists of three parts. these are:
Answers
Main Answer: A normalized binary number typically consists of three parts:
Sign bitExponentMantissaSupporting Question and Answer:
What is a sign bit in a normalized binary number?
The sign bit is the leftmost bit of a normalized binary number and indicates whether the number is positive or negative .A value of 0 indicates a positive number, while a value of 1 indicates a negative number.
Body of the Solution: A normalized binary number typically consists of the following three parts:
Sign bit: This is the leftmost bit of the number and indicates whether the number is positive or negative. A value of 0 indicates a positive number, while a value of 1 indicates a negative number.Exponent: This is the next set of bits that represent the exponent of the number in binary form. The exponent represents the power to which the base (2) is raised to obatain the actual value of the number. Mantissa: This is the remaining bits that represent the fractional part of the number in binary form. The mantissa contains the significant digits of the number, which are multiplied by the base raised to the exponent power to obtain the actual value of the number.Final Answer: A normalized binary number typically consists of three parts:
Sign bitExponentMantissaTo learn more about the sign bit in a normalized binary number from the given link
https://brainly.in/question/8955675
#SPJ4
In right triangle ABC, m ZA = 30° and m ZB = 90°. Which of the following are true?
sin(A) = sin(C)
I. sin(A) : cos(C)
III. cos(A) = cos(C)
IV. cos(A) sin(C)
A.
and II
O B.
Il and IV
)C.
I and II
IlI and IV
Reset
Next
Answers
The correct answer is option B, II and IV.
In a right triangle, the sine of an acute angle is defined as the ratio of the opposite side to the hypotenuse, and the cosine is defined as the ratio of the adjacent side to the hypotenuse. Since ZA is an acute angle, we can use the sine ratio and the cosine ratio for that angle. Similarly, we can use the sine and cosine ratios for angle C.
For option I, sin(A) = sin(C), this is not true since angle A and angle C are different and have different ratios for their opposite and adjacent sides.
For option II, sin(A) : cos(C), this is true since sin(A) = opposite/hypotenuse and cos(C) = adjacent/hypotenuse.
For option III, cos(A) = cos(C), this is not true since angle A and angle C are different and have different ratios for their adjacent sides and hypotenuse.
For option IV, cos(A) sin(C), this is true since cos(A) = adjacent/hypotenuse and sin(C) = opposite/hypotenuse.
Therefore, the correct answer is option B, II and IV.
Learn more about :
right triangle : brainly.com/question/2632981
#SPJ11
Dara drove from home to the airport to pick up her
friend and then came back home on the same route.
Her average speed on the way to the airport was
55 miles
per
hour (mph), and her average speed on
the way back home was 45 mph. If the total driving
time was 1 hour and 20 minutes, how far, in miles, is
the airport from Dara's home?
Answers
Answer:
33 miles
Step-by-step explanation:
Trip to airport:
distance = d1
speed = s1 = 55 mph
time = t1
Trip home:
distance = d2
speed = s2 = 45 mph
time = t2
We are told the same route was used for both trips, so
d1 = d2
The total time was 1 hr 20 min = 1 hr + 20/60 hr = 4/3 hr.
t1 + t2 = 4/3
t2 = 4/3 - t1
speed = distance/time
distance = speed * time
d1 = s1 * t1
d2 = s2 * t2
d1 = d2, so
s1 * t1 = s2 * t2
t2 = 4/3 - t1; s1 = 55; s2 = 45
55 * t1 = 45(4/3 - t1)
55t1 = 60 - 45t1
100t1 = 60
t1 = 0.6
The time to get the the airport was 0.6 hr. Now we find the distance.
d1 = s1 * t1
d1 = 55 * 0.6
d1 = 33
The distance is 33 miles.
The airport is at a distance of 33 miles from Dara's home.
What is the relation between speed, distance, and time?Speed is directly proportional to distance and inversely proportional to time. Its equation is given as:
Speed = Distance/Time.
The other equations, formed using this equation are:
Distance = Speed*Time
Time = Distance/Speed.
How to solve the question?In the question, we are informed that Dara drove from home to the airport to pick up her friend and then came back home on the same route. Her average speed on the way to the airport was 55 miles per hour (mph), and her average speed on the way back home was 45 mph.
We are asked to find the distance between Dara's home and the airport, if the total driving time was 1 hour 20 minutes.
We assume the distance between Dara's home and the airport to be x miles.
As she went to the airport and came back from the airport via the same route, her distance in both the cases will be x miles.
Time taken by Dara to go from home to the airport,
t1 = Distance/Speed = x/55 (Since, her average speed on the way to the airport was 55 mph).
Time taken by Dara on the way back home,
t2= Distance/Speed = x/45 (Since, her average speed on the way back home was 45 mph).
Now, total driving time can be written as,
t1 + t2,
= x/55 + x/45,
= (9x + 11x)/495,
= 20x/495,
= 4x/99.
Now, we know that this time is given as 1 hour and 20 minutes = 1 1/3 hours = 4/3 hours.
Therefore, we an write the equation:
4x/99 = 4/3,
or, x = (4*99)/(4*3) = 33.
Therefore, the airport is at a distance of 33 miles from Dara's home.
Learn more about speed, distance, and time at
https://brainly.com/question/4931057
#SPJ2
Twelve trees are equally spaced along one side of a straight road. The distance from the first tree to the sixth tree is 60 feet. What is the distance in feet between the first and last trees?
Answers
Answer:
120 feet
Step-by-step explanation:
because 60 feet x2 is 120
The distance between the first and the last tree is 132 feet.
What is an Arithmetic Progression?An arithmetic progression(A.P.) is a series, where the difference between consecutive numbers is constant.
The first term of an A.P. is denoted by a, and the common difference is denoted by d.
The nth term of an A.P. series is found using the formula:
aₙ = a + (n-1)d.
The sum of n terms of an A.P. series is found using the formula:
Sₙ = (n/2)(2a + (n-1)d)
How do we solve the given question?We are said that every tree is equally spaced. So the distance between the trees is in arithmetic progression.
With the first tree being at 0 feet from itself, our a = 0.
The distance from the first tree to the sixth tree is 60 feet, so we can say that the 6th term is 60
6th term = a + 5d
or, 60 = 0 + 5d
or, d = 60/5 = 12 feet.
To find the distance between the first tree and the last tree(12th tree), we will find the 12th term of the series,
12th term = a + (12-1)d = 0 + 11(12) = 132 feet.
∴ The distance in feet between the first and last tree is 132 feet.
Learn more about Arithmetic Progression at
https://brainly.com/question/13989292
#SPJ2
Find the values of a and b that make the following piecewise defined function both continuous and differentiable everywhere. f(x) = 3x + 4, X<-3
2x2 + ax + b. X>-3
Answers
The values of a and b that make the piecewise defined function f(x) = 3x + 4, for x < -3, and f(x) = 2x^2 + ax + b, for x > -3, both continuous and differentiable everywhere are a = 6 and b = 9.
To ensure that the piecewise defined function is continuous at the point where x = -3, we need the left-hand limit and right-hand limit to be equal. The left-hand limit is given by the expression 3x + 4 as x approaches -3, which evaluates to 3(-3) + 4 = -5.
On the right-hand side of the function, when x > -3, we have the expression 2x^2 + ax + b. To find the value of a, we need the derivative of this expression to be continuous at x = -3. Taking the derivative, we get 4x + a. Evaluating it at x = -3, we have 4(-3) + a = -12 + a. To make this expression continuous, a must be equal to 6.
Next, we find the value of b by considering the right-hand limit of the piecewise function as x approaches -3. Substituting x = -3 into the expression 2x^2 + ax + b, we get 2(-3)^2 + 6(-3) + b = 18 - 18 + b = b. To make the function continuous, b must equal 9.
Therefore, the values of a and b that make the piecewise defined function both continuous and differentiable everywhere are a = 6 and b = 9.
Learn more about piecewise
brainly.com/question/28225662
#SPJ11
Which situation could be represented by the expression 1.40x?

Answers
Answer:
B. the area of a rectangle with side lengths 1.40 and x
Step-by-step explanation:
To find the area of a rectangle, multiply the length by the width.
If 1.40 is the length, x is the width.
1.40×x=1.40x
So B is the correct answer.
Please Help! I will give Brainlyist!

Answers
Answer:
4
Step-by-step explanation:
I'm guessing it's 4
Each month the fire department hosts spaghetti feed. This month, 26 people attended the spaghetti feed. This was 2 more than twice as many people than were at the spaghetti feed last month. Write and solve an equation to determine how many people attended last month's spaghetti feed.
Answers
Answer:
You can do 26/2=13 and then 13-2=11 which means 11 people were there last months
Step-by-step explanation:
What are the 3 angle bisectors of a triangle intersect?.
Answers
The three angle bisector of a triangle intersect at a single point that point of concurrency of the angle of bisectors is called the incenter.
Given:
the 3 angle bisectors of a triangle intersect.
when three angle bisector of a triangle intersect then that point of concurrency is called incenter.
Incenter:
The incenter of a triangle is the intersection point of all the three interior angle bisectors of the triangle. In other words, it can be defined as the point where the internal angle bisectors of the triangle cross. This point will be equidistant from the sides of a triangle, as the central axis’s junction point is the center point of the triangle’s inscribed circle.
Incenter formula:
= (ax1+bx2+x3 / a+b+c , ay1+by2+y3 / a+b+c).
Learn more about the triangle here:
https://brainly.com/question/2773823
#SPJ4

Drag an answer to each box to complete this paragraph proof. can u tell me what is this for
Answers
Answer: its for an assignment
Step-by-step explanation:
A disc jockey at a school dance has equal numbers of rock and pop songs that she randomly selects from. She designs a simulation to estimate the probability that the next three songs are all rock songs. Which simulation design could she use to estimate the probability?
Answers
The disc jockey could use a Monte Carlo simulation to estimate the probability that the next three songs are all rock songs.
In this simulation, she would randomly select a rock or pop song for each of the three slots, and then repeat this process many times (e.g. 10,000 times). She could then count the number of times that all three songs were rock songs, and divide this by the total number of simulations to get an estimate of the probability.
To estimate the probability that the next three songs are all rock songs, the disc jockey could use the following simulation design:
1. Assign a number to each rock and pop song, ensuring that both genres have equal numbers.
2. Use a random number generator to select three numbers corresponding to the songs.
3. Record the genres of the chosen songs and note if all three are rock songs.
4. Repeat the simulation process multiple times (e.g., 1000 times) to obtain a larger sample.
5. Calculate the probability by dividing the number of times all three selected songs were rock songs by the total number of simulations performed.
This simulation design will help estimate the probability of the next three songs being rock songs by accounting for the equal number of rock and pop songs in the selection pool.
To learn more about probability visit;
https://brainly.com/question/30034780
#SPJ11
4\(\sqrt{-5^2-3^2\\}\)
Answers
![4[tex]\sqrt{-5^2-3^2\\}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/iwB6YDcSz9gRXwD06E2gg8OzNEJFnbua.png)
jeff lives 12 miles east of stan jeff lives 16 miles north of wei what is the shortest stan and wei can live from each other
Answers
Answer:
20 miles
Step-by-step explanation:
first, draw a diagram. Then, use the pythagorean theorem to calculate.
Ganymede, one of the moons of Jupiter, can be modeled by a sphere with a diameter of approximately 3,388 kilometers. The Moon of Earth, by comparison, can be modeled by a sphere with a diameter of approximately 1,245 kilometers. The volume of Ganymede is approximately how many times the volume of Earth’s Moon?
Answers
The volume of Ganymede is approximately 3.48 times the volume of the Moon, based on the given diameters of the two moons and the formula for the volume of a sphere.
What is volume of a sphere?The volume of a sphere is the amount of space occupied by the sphere in three-dimensional space. It can be calculated using the formula V = (4/3)πr³, where V is the volume of the sphere, r is the radius of the sphere, and π (pi) is a mathematical constant approximately equal to 3.14159. This formula states that the volume of a sphere is four-thirds of the product of pi and the cube of the sphere's radius.
In the given question,
The volume of a sphere can be calculated using the formula V = (4/3)πr³, where r is the radius of the sphere. Since we are given the diameters of the two moons, we can calculate their radii by dividing the diameters by 2. Therefore, the radius of Ganymede is 3,388/2 = 1,694 km, and the radius of the Moon is 1,245/2 = 622.5 km.
Now, we can calculate the volumes of the two moons:
V_Ganymede = (4/3)π(1694)³ ≈ 7.66 x 10^10 km³
V_Moon = (4/3)π(622.5)³ ≈ 2.2 x 10^10 km³
To find how many times larger Ganymede's volume is compared to the Moon's volume, we can divide the volume of Ganymede by the volume of the Moon:
V_Ganymede / V_Moon ≈ (7.66 x 10¹⁰) / (2.2 x 10¹⁰) ≈ 3.48
Therefore, the volume of Ganymede is approximately 3.48 times the volume of the Moon.
To know more about volume of Ganymede, visit:
https://brainly.com/question/28605508
#SPJ1
The perimeter of a rectangular garden is 48.8 feet it’s length is 12.4 what is it’s width
Answers
Answer:
12 feet
Step-by-step explanation:
Perimeter=l+l+w+w
48.8=12.4+12.4+2w
48.8=24.8+2w
2w=24, w=12 feet
2. Ms. Fallis wants to tile a kitchen counter that has an area of 2 square meters. She has 2000 square tiles with 3-centimeter sides. Does she have enough tiles to cover the counter?
Answers
Fallis has 2000 square centimeters (cm²) tiles, she does not have enough tiles to cover the entire counter.
To find out if Ms. Fallis has enough tiles to cover the counter, we need to calculate how many tiles are required to cover an area of 2 square meters.
Since the tiles have a side length of 3 centimeters, we need to convert the area of the counter to square centimeters.
1 square meter = 10000 square centimeters (cm²)
So, 2 square meters = 20000 square centimeters (cm²)
Now, we need to calculate the area of each tile:
Side length of each tile = 3 centimeters (cm)
Area of each tile = \((side length)^2\) = \((3 cm)^2\) = 9 square centimeters (cm²)
To cover the counter, we need to divide the total area of the counter by the area of each tile:
Number of tiles required = (Total area of counter) / (Area of each tile)
= 20000 cm² / 9 cm²
= 2222.22
Since we cannot have a fraction of a tile, we need to round up to the nearest whole number of tiles. So, Ms. Fallis needs at least 2223 tiles to cover the counter.
Since she has 2000 square centimeters (cm²) tiles, she does not have enough tiles to cover the entire counter.
For such more questions on square metre
https://brainly.com/question/30559154
#SPJ11