Answers
Given:
The equation is
\(\dfrac{1}{3}x=\dfrac{1}{5}\)
To find:
The coefficient and reciprocal.
Solution:
We have,
\(\dfrac{1}{3}x=\dfrac{1}{5}\)
Here, \(\dfrac{1}{3}\) is multiplied with x.
So, the coefficient of x is \(\dfrac{1}{3}\).
To find the reciprocal, we need to interchange numerator and denominator of a fraction.
So, the reciprocal of \(\dfrac{1}{3}\) is \(\dfrac{3}{1}=3\)
Therefore, the reciprocal is 3.
Related Questions
I need help please

Answers
4931870234e-238+9273.
I NEED HELP WITH PERCENT PROBLEM

Answers
Answer:
76$
Step-by-step explanation:
114=.6y; y= original price
y=190, original price
190-114=76
Write two equivalent ratios with 2 and 3
Answers
Answer
6/15, 4/6
Step-by-step explanation:
What is the sum of this equation

Answers
Answer:
The answer is A
Step-by-step explanation:
Add up
Need Help!!!! A pre-image has coordinates J(3, -6) and K(-1, -2). The image has coordinates J'(6, 3) and K'(2, -1). Describe the clockwise rotational path of the line segment.
Answers
After considering the given data we conclude that the clockwise rotational path of the line segment is a rotation of -59.04 degrees about the point (-6, -1).
We have to evaluate the center and angle of rotation to explain the clockwise rotation of the line segment.
So in the first step, we can evaluate the midpoint of the line segment JK and the midpoint of the line segment J'K'. we can calculate the vector connecting the midpoint of JK to the midpoint of J'K'. This vector is (4-1, 1-(-4) = (3,5)
The center of rotation is the point that is equidistant from the midpoints of JK and J'K'. We can evaluate this point by finding the perpendicular bisector of the line segment connecting the midpoints.
The slope of this line is the negative reciprocal of the slope of the vector we just found, which is -3/5. We can apply the midpoint formula and the point-slope formula to evaluate the equation of the perpendicular bisector:
Midpoint of JK: (1, -4)
Midpoint of J'K': (4, 1)
The slope of the vector: 3/5
(x₁ + x₂)/2, (y₁ + y₂) /2
Point-slope formula: y - y₁ = m(x - x₁)
Perpendicular bisector: y - (-4) = (- 3/5)(x - 1)
Applying simplification , we get: y = (- 3/5)x - 1.2
To evaluate the center of rotation, we need to find the intersection point of the perpendicular bisector and the line passing through the midpoints of JK and J'K'. This line has slope ( 3 - (4)) /(4 - 1) = 7/3 and passes through the point (4, 1). Applying the point-slope formula, we can evaluate its equation:
y - 1 = (7/3)( x - 4)
Apply simplification , we get: y = (7/3)x - 17/3
To evaluate the intersection point, we can solve the system of equations:
y =(- 3/5)x - 1.2 = (7/3)x - 17/3
Evaluating for x and y, we get x = -6 and y = -1.
Therefore, the center of rotation is (-6, -1).
√( 4 - 1)² + ( 1 - ( - 4))²) = 5√(2)
Distance between image points and center of rotation
√( ( 6 - (-6))² + ( 3 - (-1))² = 13
The ratio of these distances gives us the scale factor of the transformation, which is 13/√2).
The angle of rotation is negative as the image moves clockwise direction. We can apply the inverse tangent function to find the angle of the vector connecting the midpoint of JK to the midpoint of J'K':
Angle of vector: arctan(5/3) = 59.04 degrees
Therefore, the clockwise rotational path of the line segment is a rotation of -59.04 degrees about the point (-6, -1).
To learn more about midpoint formula
https://brainly.com/question/30276996
#SPJ1
Find the Central Angle
mXY = = 18 in
radius ZY = 7.64 in
Answers
The central angle is approximately 2.357 radians.
To find the central angle, we can use the formula:
Central angle (θ) = arc length ÷ radius
Given:
Arc length (mXY) = 18 in
Radius (ZY) = 7.64 in
Plugging in the values:
Central angle (θ) = 18 in ÷ 7.64 in
Calculating the division:
θ ≈ 2.357 radians
Therefore, the central angle is approximately 2.357 radians.
To know more about Central Angle:
https://brainly.com/question/3293818
An investment, initially worth £645.3, grows at a constant continuous rate of 0.05. After how many years will it be
worth £29437.2? (find t)
Give your answer to 1 decimal place
Answers
The investment growth is an illustration of an exponential function.
It will take 78.3 years for the investment to reach £29437.2
The given parameters are:
Initial worth: 645.3Rate: 0.05Exponential functionsAn exponential function is represented as:
\(y = a(1 + r)^t\)
Where:
a represents the initial valuer represents the rate.The number of yearsSo, we have:
\(y = 645.3(1.05)^t\)
When the investment becomes 29437.2, the equation becomes
\(29437.2 = 645.3(1.05)^t\)
Divide both sides by 645.3
\(45.6=1.05^t\)
Take the logarithm of both sides
\(\log(45.6)=\log(1.05)^t\)
This gives
\(\log(45.6)=t\log(1.05)\)
Make t the subject
\(t = \frac{\log(45.6)}{\log(1.05)}\)
\(t = 78.3\)
Hence, it will take 78.3 years for the investment to reach £29437.2
Read more about exponential functions at:
https://brainly.com/question/11464095
What is the value of -
3x + 2(y - 1)
when x = 4 and y = 3?
x + y²
Show your work.
Answers
Answer:
-8
Step-by-step explanation:
substitute
x=4
into -3x+2(y-1):
x=3
-3x4+2x(3-1)
-12+2x(3-1)
-12+2x2
-12+4
= -8
Answer:
first question ans is 16 and second is 13
Step-by-step explanation:
Given
x=4 and y=3
3x+2(y-1)
3×4+2(3-1)
3×4+2×2
12+4
16Ans
Second question is
x+y×y
4+3×3
4+9
13 Ans
Look at the tree shown in the diagram. What is the bight of the tree rounded to the nearest tenth foot?

Answers
Answer:
Correct answer is B, 69.3 feet
Step-by-step explanation:
Since we have a 30°-60°-90° right triangle, the length of the longer leg is √3 times the length of the shorter leg, so the length of the shorter leg is 1/√3, or √3/3 times the length of the longer leg.
\(120( \frac{ \sqrt{3} }{3}) = 40 \sqrt{3} = 69.3\)
Compare the motion of the boy and the man. Who was going faster? Was their acceleration about the same? Who had more frictional force? What might have caused the difference in frictional force?
Answers
Answer:
Both of there acceleration was about the same.
I think the man had more frictional force because he was heavier than the boy
Step-by-step explanation:
Answer:
Answer:
Both of there acceleration was about the same.
I think the man had more frictional force because he was heavier than the boy
Step-by-step explanation:
can someone tell me which expression is equivalent ?

Answers
Answer:
D. 12h + 6k
Step-by-step explanation:
in order to find the equivalent expression, you have to simplify it (at least in this case)
when simplifying the expression, you use the distributive property (multiplying 3 to both 4h AND 2k). 3(4h) = 12h, and 3(2k) = 6k, so it is 12h + 6k
Please help find the area

Answers
The triangle's area is listed as: 70.50cm2.A shape's surface area is measured by its area.
What explains the above-mentioned resolution?A shape's surface area is measured by its area.By multiplying the length and breadth of a rectangle or square, you can get its area.Area A is equal to x times y.
Square measurements, such as square inches, square feet, or square meters, are used to describe area.Multiplying a rectangle's length and breadth will reveal its area.A is the area, L is the length, W is the width, and * denotes multiply in the formula.
Area of the darkened area is equal to the sector's area minus the triangle's area.This is displayed as:π r² (∅/360) - 1/2 x b x h
= π x 14² x (46/360) - (1/2) x 14 x 10.0708
= 78.6794 - 70.4956
= 8.1838 cm²
Consequently, the triangle's area is equal to (1/2) x 14 x 10.0708.
= 70.4956 cm²
To learn more about triangle's area refer
https://brainly.com/question/21735282
#SPJ1
Which number has a 6 that is 1/10 the value of the 6 in 6,239
Answers
Answer:
it is b
Step-by-step explanation: hope help
PLEASE ANSWER ASAP FOR BRAINLEST!!!!!!!!!!!!!!!!!!!!!!
The length of each of the two congruent sides of an isosceles triangle is 2x + 3. The length of the third side is 2x. Its perimeter is 36 centimeters. Write an equation that could be used to find the value of x. Solve for x and then find the length of all three sides.
Answers
Answer:
the equation: 2x+3+2x+3+2x= 36
x=5
the length of the congruent sides
15
the length of the third side
10
Step-by-step explanation:
i'll add this later hold on
what is bigger 1 yard or 35 inches
Answers
Answer:
1 yard
Step-by-step explanation:
in a yard there is 36 inches
turning improper fractions into mixed numbers 2 1/6 4 1/2
Answers
ANSWERS:
2 1/6= 12/6
4 1/2= 8/2
If 98 is added to a number, the result is 36 less than three times the number. Find the number.
Answers
Answer:
\(\tex\huge\boxed{67}\)
Step-by-step explanation:
In order to solve this problem, we should set it up in an algebraic equation. Doing so will make it easier to make sense of the problem. To do this, we can represent each part of the statement with an expression.
For the purposes of this, let's call our unknown number \(n\).
If 98 is added to a number = \(n+98\)The result is, =36 less than 3 times the number = 3n - 36
Altogether, we get \(n+98=3n-36\). We can now solve for \(n\).
Remove the \(\bold{n}\) term from one side. \(n+98 - n = 3n -36 - n\) \(98 = 2n-36\)Isolate the \(\bold{n}\) term. \(98+36=2n-36+36\)\(134=2n\)Get \(\bold{n}\) by itself. \(134 \div 2 = 2n \div 2\)\(67=n\)Therefore, the answer here is 67.
Hope this helped!
Absolute value functions have vertical line
symmetry.
_______
True
or
False

Answers
Answer:
True
Step-by-step explanation:
Can anyone teach mee.....................

Answers
Answer:
(i) The name of the part of the circle, OQ is a radius
(ii) The radius of the sector QOR is 21 cm
Step-by-step explanation:
The given figure is a sector of the circle O
∵ Any sector of a circle formed from 2 radii and an arc
∴ OQ is a radius
(i) The name of the part of the circle, OQ is a radius
The rule of the length of an arc of a circle is L = \(\frac{\alpha }{360}\) × 2 π r, where
α is the angle of the sectorr is the radius of the circle∵ The length of the arc QR is 22 cm
∴ L = 22
∵ The measure of the angle of the arc is 60°
∴ α = 60°
∵ π = \(\frac{22}{7}\)
→ Substitute them in the rule above
∵ 22 = \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × r
∴ 22 = \(\frac{22}{21}\) r
→ Divide both sides by \(\frac{22}{21}\)
∴ 21 = r
(ii) The radius of the sector QOR is 21 cm
Can you help?? Please
Answers
Answer:
2×100= 200
1349×10=13490
A2+B2=C2
1. There are 78 sophomores at a school. Each is required to take at least one year of either chemistry or physics, but they may take both. 15 are enrolled in both chemistry and phys- ics, and 47 are enrolled only in chemistry. How many students are enrolled only in physics?
Answers
We are given that there are a total of 78 students. If we set the following variables:
\(\begin{gathered} C=\text{students only in chemestry} \\ P=\text{students only in physics} \\ PC=\text{students in physics and chemistry} \end{gathered}\)Then, the sum of all of these must be 78, that is:
\(C+P+PC=78\)Since there are 15 in chemistry and physics and 47 in chemistry, we may replace that into the equation and we get:
\(47+P+15=78\)Simplifying:
\(62+P=78\)Now we solve for P by subtracting 62 on both sides:
\(\begin{gathered} 62-62+P=78-62 \\ P=16 \end{gathered}\)Therefore, there are 16 students in physics
What is 2 plus 4 please help
Answers
Answer:
It is, 6
Step-by-step explanation:
Good luck! Have a good day!! <33
Act like you have 2 fingers up and then add 4 more.
At colleges in Jacksonville, do tennis coaches generally get paid more than football coaches?
Answers
It is difficult to make a general statement about whether tennis coaches generally get paid more than football coaches in Jacksonville or elsewhere, as the salaries of coaches are influenced by a Wide range of factors
As an AI language model, I do not have access to up-to-date information about salaries of coaches in Jacksonville. However, in general, the salaries of coaches vary widely depending on a number of factors, such as the type of sport, the level of competition, the location, the success of the team, and the budget of the institution.
In terms of tennis and football, football is generally considered to be a more popular and high-profile sport than tennis in the United States, which could result in higher salaries for football coaches at the collegiate level. Football also typically generates more revenue and has larger budgets for athletic programs, which could also influence the salaries of coaches.
However, there are also factors that could affect the salaries of tennis coaches. For example, if a tennis program has a particularly successful season or has produced successful players, the coach may negotiate a higher salary. Additionally, some colleges may place a greater emphasis on tennis or have larger budgets for tennis programs, which could also impact the salaries of coaches.
Overall, it is difficult to make a general statement about whether tennis coaches generally get paid more than football coaches in Jacksonville or elsewhere, as the salaries of coaches are influenced by a wide range of factors. It is also important to note that salaries can vary widely between individual institutions, even within the same sport, and that negotiations between coaches and their institutions can play a significant role in determining salaries.
To know more about Wide range.
https://brainly.com/question/30389189
#SPJ11
The function f(x) = a^x + 4 will never cross the x-axis if a is positive. True or False?
Answers
Answer:
True
Step-by-step explanation:
If a is negative then the shape of the graph is an upside down U, which intersects the x-axis. If a is positive it will never cross the X axis.
It is true that f(x)=\(a^{x}\)+4 will never cross the x axis if a is positive.
What is function?Function is relationship between two or more that are variables expressed in equal to form. In a function each value of x must have a corresponding value of y.
How to find x intercept?We have been given that f(x)=\(a^{x} +4\) and we have to find whether it will cross x axis or not.
when a line crosses the x axis the value of y becomes negative. We have to first check at y=0.
\(a^{x}+4\)=0
\(a^{x}\)=-4
taking log both sides,
log \(a^{x}\)=log(-4)
x log a=0.602059991+1.3437635i
x=(0.602059991+1.3437635i)/log a
when we put the value of x in f(x) the value of f(x) cannot be negative so it cannot crosses the x axis.
Hence it is true that f(x)=\(a^{x}\)+4 will never cross the x axis if a is positive.
Leaarn more about function at https://brainly.com/question/10439235
#SPJ2
What is the approximate area of a circle with radius 6 cm?

Answers
Answer:
133 m^2
Step-by-step explanation:
to find are of a circle it’s r^2 times pi
6^2 x pi
36 pi
113 m^2
Hopes this helps please mark brainliest
Answer:
Answer C is correct
Step-by-step explanation:
The formula to find the area of a circle is:
A = πr²
Here,
r => radius = 6m
Let us find the area of the circle.
A = πr²
A = 3.14 × 6 × 6
A = 113.04 m²
Approx. = 113m²
Bria is a customer who would like to display her collection of soap carvings on top of her bookcase. The collection needs an area of 300 square inches. What should b equal for the top of the bookcase to have the correct area? Round your answer to the nearest tenth of an inch.
I need help D: Please !!!!

Answers
The width of the top of the bookcase should be approximately 12.2 inches to give Bria's soap carving collection an area of 300 square inches.
How do you compute the area of a square inch?Simply multiply the length and width measurements to get the area of your square or rectangular area in square inches.
Assume the bookcase's top is rectangular, with length "L" and width "b". Because the area of a rectangle is the product of its length and width, we get:
L * b = 300
To find "b," we can rearrange the equation as follows:
b = 300 / L
We don't have enough information to directly solve for "L," but we can make an educated guess based on the figure provided. Based on the illustration, the bookcase appears to be roughly twice as long as it is wide. So let us suppose:
L ≈ 2b
When we plug this into the equation above, we get:
b = 300 / (2b) (2b)
To simplify, we have:
b^2 = 150
When we take the square root of both sides, we get:
b ≈ 12.2
We have, rounded to the nearest tenth of an inch:
b ≈ 12.2 inches
As a result, the width of the top of the bookcase should be approximately 12.2 inches in order to give Bria's soap carving collection a 300-square-inch area.
To know more about Area of Square Inches visit:
https://brainly.com/question/7742557
#SPJ1
Which pair shows equivalent expressions?
O 24x+2)-2x+1
O 2(3x+2)= x+4
o 21&x+4)= 4x+2
o 21

Answers
Answer:
Your answer is
\(2 (\frac{2}{5} x + 2) = \frac{4}{5} x + 4\)
WILL MARK BRAINLIEST
Use the function below to find F(3)
F(x)=(1/5)^x

Answers
The value of the function F(3) will be 1/125. It is obtained by putting the value 3 in the place of x.
What is a function?A connection between independent variables and the dependent variable is defined by the function. Functions help to represent graphs and equations.
A function is represented by the two variables one is dependent and another one is an independent function. The relation between them is shown as y if dependent and x is the independent variable.
F(x)=(1/5)ˣ
F(3)=(1/5)³
F(3)=1/125
Hence, the value of the function F(3) will be 1/125.
To learn more about the function refer to the link
https://brainly.com/question/12431044.
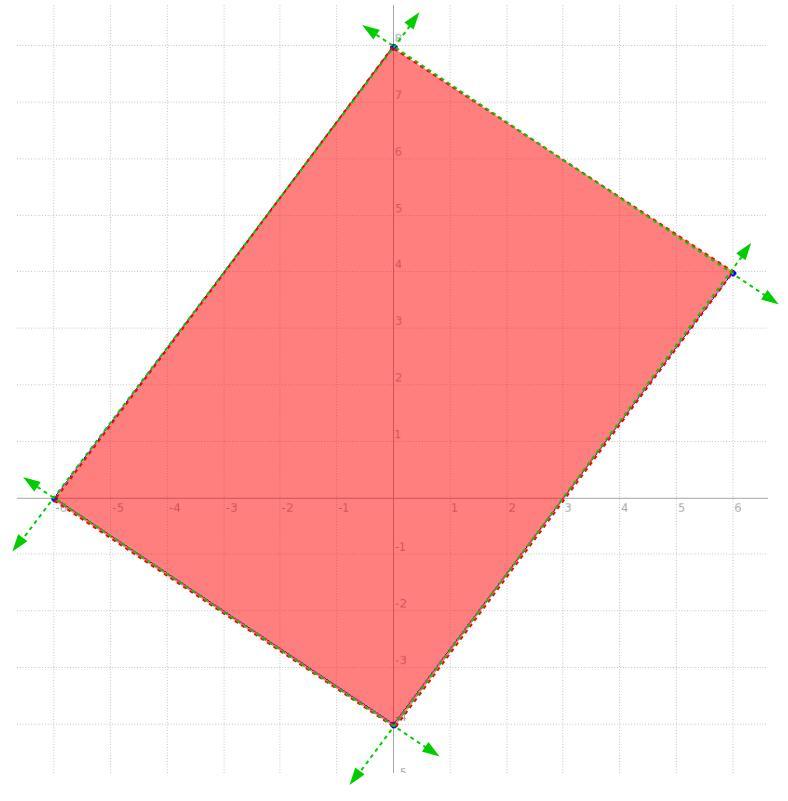
HELP PLEASE I DONT GET THIS

Answers
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
Which triangle is similar to △JKH?
1. △MKN
2. △JOG
3. △MQL
4. All triangles are similar to △JKH

Answers
Given that Line a is parallel to Line b (Line a ║ Line b), the triangle that is similar to ΔJKH is 1. ΔMKN
What are similar triangles in geometry?Similar triangles are triangles that have congruent corresponding angles, and in which all three corresponding sides are proportional.
The given parameter is Line a is parallel to Line b, which gives: a║b
Two triangles are similar if they satisfy the following conditions:
Two angles in one triangle are equal to two angles in the other triangle.Each of the three corresponding sides of the two triangles are proportional.Two sides of one triangle are proportional to the corresponding two sides on the other triangle, and the included angle between the specified two sides in both triangles are congruent.According to alternate angles theorem, the angles ∠JHK in ΔJKH is congruent to the ∠KNM in triangle ΔMKN
Similarly, the angle ∠HJK in ΔJKH is congruent to the ∠KMN in ΔMKN
Therefore, ΔJKH is similar to ΔMKN by Angle-Angle, AA similarity postulate.
The correct option for the triangle similar to ΔJKH is option 1. ΔMKN
Learn more about similar triangles in geometry here:
https://brainly.com/question/14285697
#SPJ1
