PLEASE HELP ME IM DOING A TEST :Write in point-slope form an equation of the line that passes through the point (5, 9) with slope 7. ____
Answers
Answer:
y-9+7(x-5)
Step-by-step explanation:
y - x1 = m ( x - y1 )
Y1 = 9
x1 = 5
m=slope (in this case 7)
Answer:
[7x-y-26=0]
Step-by-step explanation:
point slope form =
y-y1=m(x-x1)
=
y-9=7(x-5)
=
[7x-y-26=0]
you may want the y-9=7(x-5) as your answer
second part of this is for vertex form
/////// vertex form ///////Use formula y=mx+b where m is slope
y is equal to 9
x is equal to 5
b=?
m=7
9=7*5+b ---> b= -26
////////////////
Related Questions
PLS HELP FAST
Points X and Y lie on (circle)P so that PX = 5 meters and m∠XPY = 90. Find the length of XY to the nearest hundredth.
Answers
Step-by-step explanation:
P means the center of the circle.
any point on the circle has therefore a constant distance from the center : the radius r.
r = 5 m
what we need to find is the length of the circle arc between the 2 points that represents 90° of the overall circle (360°).
90/360 = 1/4
so, we are looking for 1/4 of the overall circle circumference :
2×pi×r × 1/4 = 2×pi×5 × 1/4 = pi×10/4 = pi×5/2 =
= 7.853981634... m ≈ 7.85 m
what is the area of this traingle of 12 in of height and 3 in of base iready
Answers
Answer:
Triangle area formula is base x height /2
Step-by-step explanation:
12 x 3 = 36
36/2 = 18
A = 18
Mark Brainliest!
which ratio is equivalent to 12:20?
a) 3:5
b) 20:12
c) 3:10
d) 2:3
Answers
Answer:
D
Step-by-step explanation:
Answer:
it is a 3:5
Step-by-step explanation:
A single tractor-trailer driver is starting a new shift, intending to travel 450 miles from Charlotte, NC to Pittsburgh, PA. Estimating an average speed of 50 mph and abiding by the current HOS rules, what is the minimum number of clock hours (not driving hours) it will take him?
Answers
It will take a minimum of 10 clock hours (not driving hours) for the truck driver to travel 450 miles from Charlotte, NC to Pittsburgh, PA.
The current Hours of Service (HOS) rules for truck drivers stipulate that a truck driver cannot drive for more than 11 hours after 10 consecutive hours off duty.
Additionally, the driver is not allowed to drive beyond 14 hours after coming on duty.
The driver's shift includes both driving and non-driving time.
Therefore, it is necessary to consider the total amount of time spent on the job.
The truck driver will have to stop for rest breaks, refueling, or other reasons during the 450-mile journey to Pittsburgh, Pennsylvania. The driver is required to take a 30-minute break after eight hours of driving.
Therefore, the minimum number of clock hours (not driving hours) it will take the truck driver to travel the 450-mile distance from Charlotte, NC to Pittsburgh, PA is calculated as follows:
Time for the trip = (Distance ÷ Average Speed) + Breaks
Time for the trip = (450 ÷ 50) + (30 ÷ 60) × 2
Time for the trip = 9 + 1
Time for the trip = 10 clock hours
Therefore, it will take a minimum of 10 clock hours (not driving hours) for the truck driver to travel 450 miles from Charlotte, NC to Pittsburgh, PA.
Know more about Hours of Service (HOS) here:
https://brainly.com/question/32726922
#SPJ11
Write an exponential model for this data set and find out how many years it will take to have 51,200 squirrels in the forest.
Answers
It will take 20.78 years to have 51,200 squirrels in the forest, according to the exponential model N(t) = N0e^(kt), where N(t) is the number of squirrels at time t, N0 is the initial number of squirrels (in this case, 400), and k is the growth rate.
The exponential model for this data set can be expressed as: N(t) = N0e^(kt), where N(t) is the number of squirrels at time t, N0 is the initial number of squirrels (in this case, 400), and k is the growth rate. To find out how many years it will take to have 51,200 squirrels in the forest, we can solve for t, yielding t = ln(51,200/400)/k. We can solve for k by rearranging the equation and plugging in our data points, which yields k = ln(1300/400)/5 = 0.25. Therefore, the number of years it will take to have 51,200 squirrels in the forest is t = ln(51,200/400)/0.25 = 20.78 years.
Therefore, It will take 20.78 years to have 51,200 squirrels in the forest, according to the exponential model N(t) = N0e^(kt), where N(t) is the number of squirrels at time t, N0 is the initial number of squirrels (in this case, 400), and k is the growth rate.
Learn more about growth rate here:
https://brainly.com/question/6424007
#SPJ4
Will mark brainliest answer!
Ben wants to buy a new car stereo and he has already saved some money. He used this inequality to represent the amount he still has to save to be able to buy the stereo, where a represents the amount still left to save.
a + 212 greater-than-or-equal-to 365
If Ben saves $15 a week for the next 10 weeks, will he be able to buy the stereo and why?
No, because he needs to save at least $153, and he will only save $150 over the next ten weeks.
No, because he needs to save $577, and he will only save $150 more.
Yes, because he has already saved $365, and the stereo cost $212.
Yes, because he has already saved $212, and he will save another $150.
Answers
Answer:
No, because he needs to save at least $153, and he will only save $150 over the next ten weeks.
Step-by-step explanation:
Brainliest?
Answer:
the answer is A
Step-by-step explanation:
i got it right on the quiz
Use your graphing calculator for the following problems.
3) Javier wants to invest $3,000 in a mutual fund. He finds an international fund that earns
6% per year. The following function equation represents the account balance for Javier's
mutual fund over time: f(t)=3,000 (1.06)'.
a. Fill in the given table of values with at least five points generated from the function equation.
(Round values to the nearest tenth.)
Variables
Time
(years)
Values
Process
Account
Balance ($)
0
2
8
13
18
b. Graph the given exponential function on the coordinate plane provided. Label the x- and
y-axes with appropriate units and scales, if not provided.

Answers
The amount in the account after 18 years from the given function is $8563.0.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
Given that, Javier wants to invest $3000 in a mutual fund.
An international fund that earns 6% per year.
The function to represent the account balance is \(f(t)=3000(1.06)^t\).
Substitute t=0, 2, 8, 13, 18
When t=0,
f(0)=3000(1.06)⁰
f(0)=$3000
When t=2
f(2)=3000(1.06)²
f(2)=$3370.8
When t=8
f(8)=3000(1.06)⁸
f(8)=$4781.54
When t=13
f(13)=3000(1.06)¹³
f(13)=$6398.78
When t=18
f(18)=3000(1.06)¹⁸
f(18)=$8563.0
Therefore, the amount in the account after 18 years is $8563.0.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1

PLEASE HELP NEED IT DONE RN !!

Answers
Answer: rectangleular pyramid
Step-by-step explanation:
If the diameter of a frisbee is 10 inches, how much is its circumference?
Answers
Answer:
the circumference is 31.4
Step-by-step explanation:
The computation of the circumference is shown below:
As we know that
Circumference is
= 2πr
= 2π (10 ÷ 2)
= 2× 3.14 × 5
= 31.4
Hence, the circumference is 31.4
Somebody please help me

Answers
Answer:
80% increase
Step-by-step explanation:
First, divide $0.25/$0.45, you get 0.8, turn it into a percent. 0.8=80%
There is an 80% increase.
Check work:
0.25x1.8=0.45
We multiply by 1.8 because 80% increase means 100% (itself) multiplied by 80% of itself, which gives us 180% or 1.8.
0.25x1.8=0.45 ✔️
Hope this helps!
:)
3+g=a/3h
what does a equal
Answers
Answer:
a = 3gh+9hStep-by-step explanation:
\(3+g = \frac{a}{3h} \\\\Cross\:Multiply\\\\3h(3+g) = a\\9h +3gh = a\\\\a = 3gh+9h\)
Use the simplex method to solve the linear programming problem Maximize z=7X1 + 5x2 + x3 subject to 5x1 +5x2 + x3 = 25 x1 + 3x2 + 5x3 = 13 x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
Select the correct choice below and if necessary, fill in the answer boxes to complete your choice A. The maximum is when x1= x2= s1= and s2=
B. There is no maximum
Answers
The value will be maximum when x1 = 3, x2 = 2, s1 = 0, and s2 = 0.
To solve the linear programming problem using the simplex method, we need to convert the problem into standard form by introducing slack variables. The standard form of the given problem becomes:
Maximize z = 7x1 + 5x2 + x3
subject to
5x1 + 5x2 + x3 + s1 = 25
x1 + 3x2 + 5x3 + s2 = 13
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, s1 ≥ 0, s2 ≥ 0
The initial tableau for the simplex method is:
| Cb | x1 | x2 | x3 | s1 | s2 | RHS |
|----|----|----|----|----|----|-----|
| 0 | -7 | -5 | -1 | 0 | 0 | 0 |
| s1 | 5 | 5 | 1 | 1 | 0 | 25 |
| s2 | 1 | 3 | 5 | 0 | 1 | 13 |
Performing the simplex iterations, we find:
Iteration 1:
Pivot Column: x1 (most negative coefficient in the objective row)
Pivot Row: s1 (minimum ratio in the right-hand side column)
Pivot Element: 5 (intersection of pivot column and pivot row)
| Cb | x1 | x2 | x3 | s1 | s2 | RHS |
|---- |----|----|----|----|----|-----|
| s1 | 1 | 1 | 0 | 1 | 0 | 5 |
| x2 | 0 |2 | 1 | -1 | 0 | 20 |
| s2 | 0 | 2 | 5 | 1 | 1 | 8 |
Iteration 2:
Pivot Column: x2 (most negative coefficient in the objective row)
Pivot Row: s2 (minimum ratio in the right-hand side column)
Pivot Element: 2/5 (intersection of pivot column and pivot row)
| Cb | x1 | x2 | x3 | s1 | s2 | RHS |
|----|----|----|----|----|----|-----|
| s1 | 1 | 0 | -1/5 | 3/5 | -2/5 | 1 |
| x2 | 0 | 1 | 2/5 | -1/5 | 2/5 | 4 |
| s2 | 0 | 0 | 17/5 | 3/5 | 1/5 | 4 |
All coefficients in the objective row are non-negative, indicating that the optimal solution has been reached. The maximum value of z is 4, and the corresponding values for x1, x2, s1, and s2 are 3, 2, 0, and 0, respectively.
Therefore, the maximum is when x1 = 3, x2 = 2, s1 = 0, and s2 = 0.
To know more about linear programming refer here:
https://brainly.com/question/30763902?#
#SPJ11
rove the following identity for any positive n≥1 ∑
i=1
n
∑
j=1
i
2=n(n+1) 2. Solve the following recurrence and prove the solution correct by induction:
T(1)
T(n)
=4c
=2cn+T(n/2).
3. You are given the function g(n)=nlogn. for each function f(n) below prove or disprove that f(n)=O(g(n)) a) f(n)=3n
2
b) f(n)=4n c) f(n)=6nlogn+5n d) f(n)=(logn)
2
Answers
a) f(n) = 3n^2 is not O(g(n))
b) f(n) = 4n is O(g(n))
c) f(n) = 6nlog(n) + 5n is O(g(n))
d) f(n) = (log(n))^2 is not O(g(n))
1. Proof of the identity ∑[i=1 to n] ∑[j=1 to i] 2 = n(n+1)/2:
Let's evaluate the double sum on the left-hand side:
∑[i=1 to n] ∑[j=1 to i] 2
We can rewrite this as:
∑[i=1 to n] (2i)
Now, let's simplify the right-hand side of the equation:
n(n + 1)/2
Expanding the expression, we get:
\((n^2 + n)/2\)
To prove the identity, we need to show that the double sum on the left-hand side is equal to the expression on the right-hand side.
Let's evaluate the double sum:
∑[i=1 to n] (2i) = 2(1) + 2(2) + ... + 2(n)
Using the formula for the sum of an arithmetic series, we have:
∑[i=1 to n] (2i) = 2(1 + 2 + ... + n) = 2[(n(n + 1))/2] = n(n + 1)
We have shown that the left-hand side is equal to n(n + 1), which matches the expression on the right-hand side. Therefore, the identity is proven.
2. Solution to the recurrence T(1) = 4c, T(n) = 2cn + T(n/2):
To solve the recurrence relation, we can use the method of recursion tree and prove the solution by induction.
Step 1: Guess the solution: We assume that the solution to the recurrence relation is T(n) = knlogn for some constant k.
Step 2: Base case: T(1) = 4c (given). Plugging in n = 1 in the assumed solution, we have:
T(1) = k(1)log(1) = k(0) = 4c
From this, we can deduce that k = 4c.
Step 3: Inductive step: Assume that the solution holds for T(n/2), i.e., T(n/2) = (4c)(n/2)log(n/2).
Now, let's compute T(n) using the given recurrence relation:
T(n) = 2cn + T(n/2) = 2cn + (4c)(n/2)log(n/2)
Simplifying further, we get:
T(n) = 2cn + 2cnlog(n/2) = 2cn(1 + log(n/2))
Using log property, we can write log(n/2) as log(n) - log(2) = log(n) - 1.
Substituting this back into the equation, we have:
T(n) = 2cn(1 + log(n) - 1) = 2cnlog(n)
We have shown that T(n) = 2cnlog(n), which matches our assumed solution.
Step 4: By induction, we have proven that the solution to the recurrence relation T(1) = 4c, T(n) = 2cn + T(n/2) is T(n) = 2cnlog(n).
3. Proving or disproving f(n) = O(g(n)) for the given functions:
a) \(f(n) = 3n^2\)
To prove or disprove f(n) = O(g(n)), we need to show that there exist constants c and n0 such that f(n) <= c * g(n) for all n >= n0.
Let g(n) = nlog(n). Let's evaluate the limit of f(n)/g(n) as n approaches infinity:
\(lim (n- > ∞) (3n^2 / (nlog(n))) = lim (n- > ∞) (3n / log(n))\)
Using L'Hôpital's rule, we differentiate the numerator and denominator:
lim (n->∞) (3 / (1/n)) = lim (n->∞) (3n) = ∞
Since the limit is not finite, we can conclude that \(f(n) = 3n^2\) is not O(g(n)).
b) f(n) = 4n
Similarly, let's evaluate the limit of f(n)/g(n) as n approaches infinity:
lim (n->∞) (4n / (nlog(n))) = lim (n->∞) (4 / log(n))
Again, using L'Hôpital's rule:
lim (n->∞) (0 / (1/n)) = lim (n->∞) (0) = 0
Since the limit is finite, we can conclude that f(n) = 4n is O(g(n)).
c) f(n) = 6nlog(n) + 5n
Evaluating the limit:
lim (n->∞) ((6nlog(n) + 5n) / (nlog(n))) = lim (n->∞) ((6log(n) + 5) / log(n))
Using L'Hôpital's rule:
\(lim (n- > ∞) ((6 / (1/n)) / (1/n)) = lim (n- > ∞) (6) = 6\)
Since the limit is finite, we can conclude that f(n) = 6nlog(n) + 5n is O(g(n)).
d) \(f(n) = (log(n))^2\)
Evaluating the limit:
\(lim (n- > ∞) (((log(n))^2) / (nlog(n))) = lim (n- > ∞) ((2log(n)/n) / (1/n)) = lim (n- > ∞) (2log(n)) = ∞\)
Since the limit is not finite, we can conclude that \(f(n) = (log(n))^2\) is not O(g(n)).
To know more about log refer here:
https://brainly.com/question/32621120
#SPJ11
What is the following quotient?
5 sqrt 11 - sq rt 3
Answers
We need to rationalize the denominator by multiplying both the numerator and the denominator by the conjugate of
which is
When we rationalize we obtain:
The denominator is now a difference of two squares:
We apply this property to get
This simplifies to
Or
At which speed will a car travel in 2hours 35minutes if it traveled 2hours 45minutes at a speed of 106km/hour
Answers
The speed at which a car travel in 2hours 35minutes if it travelled 2hours 45 minutes at a speed of 106 km/hour is 112.8 km/hour.
The algorithm is as follows:
speed = Distance / Time
Distance = speed * time.
Distance = 106 km/h * 2.75 hours
Distance = 291.5 km
Now we can apply the algorithm determine the vehicle's overall speed:
Speed = Distance / Time
The Total time = 2 hours 35 minutes = 2.5833 hours
Speed = Distance / Total time
Speed = 291.5 km / 2.5833 hours
Speed = 112.8 km/h
The vehicle will therefore with the speed of approximately 112.8 km/h for the duration of the 2 hours 35 minute trip.
Learn more about speed here:
https://brainly.com/question/28224010
#SPJ4
I want to know how to do this problem

Answers
Answer:
Step-by-step explanation: k = 25
Find an equation of the line parallel to Y = 2x+3 and that passes through the point (5,3)
Answers
Find the linearization L(x) of the function at a. T f(x) = 7cos(x), a = - (Consider a=3.14159265359 ) 9 L(x)"
Answers
To find the linearization L(x) of the function f(x) = 7cos(x) at a = 3.14159265359, we'll use the formula:
L(x) = f(a) + f'(a)(x - a)
where f'(x) is the derivative of f(x) with respect to x.
First, let's find the value of f(a) at a = 3.14159265359:
f(a) = 7cos(a)
f(3.14159265359) = 7cos(3.14159265359) ≈ -7
Next, let's find the value of f'(a) at a = 3.14159265359:
f'(x) = -7sin(x)
f'(a) = -7sin(a)
f'(3.14159265359) = -7sin(3.14159265359) ≈ 0
Now we have all the pieces we need to plug into the formula for L(x):
L(x) = f(a) + f'(a)(x - a)
L(x) = -7 + 0(x - 3.14159265359)
L(x) = -7
So the linearization of the function f(x) = 7cos(x) at a = 3.14159265359 is:
L(x) = -7
To find the linearization L(x) of the function f(x) = 7cos(x) at a specific point a, we'll use the formula:
L(x) = f(a) + f'(a)(x - a)
Given that a = 3.14159265359 (approximating π), first we need to find f(a) and f'(a).
1. f(a) = 7cos(a) = 7cos(3.14159265359) ≈ -7
2. To find f'(x), we take the derivative of f(x):
f'(x) = -7sin(x)
Now, we can find f'(a):
f'(a) = -7sin(3.14159265359) ≈ 0
Finally, we can plug these values into the linearization formula:
L(x) = -7 + 0(x - 3.14159265359)
Simplifying, we get:
L(x) = -7
Learn more about linearization here: brainly.com/question/15830007
#SPJ11
3. If A = 49° and a = 10, find c.
Answers
The triangle is solved using the law of sines and c = 13.25
Given data ,
Let the triangle be represented as ΔABC
Now , the measure of sides of the triangle are
The measure of ∠BAC = 49°
The measure of ∠ACB = 90°
And , the measure of side a = 10 units
From the law of sines ,
a / sin A = b / sin B = c / sin C
10 / sin 49° = c / sin 90°
The triangle is solved using the law of sines , where the measure of sine of angle opposite to the sides are in the same ratio.
The trigonometric value of sin 90° = 1
c = 10 / 0.75470958022
c = 13.25 units
Therefore , the measure of c = 13.25 units
Hence , the triangle is solved and c = 13.25 units
To learn more about law of sines click :
https://brainly.com/question/13098194
#SPJ1
The complete question is attached below :
If A = 49° and a = 10, find c.

of the 60 questions, I got 80% right...How many questions did I get right?
Answers
Therefore you got 48 questions right.
the product of two consecutive integers is 420. which quadratic equation can be used to find x, the lesser number? x2 1
Answers
The quadratic equation, x(2) + 2 =420 can be used to find x.
you can use trial and error
x(2) + 2 =420
210(2)=420 but we need to add the two so lower the \(120\)
209(2)=418+2 = 420
so, the x value must less than 21.
How do you write a quadratic equation in standard form?A quadratic equation with variable x is written in standard form as \(ax2 + bx + c = 0\), where a, b, and c are constants such that the value of an is non-zero but the values of b and c can both be zeros.
Let's change \(ax2 + bx + c = 0\) from its standard form to its vertex form, which is \(a (x - h)2 + k = 0\), where (h, k) is the vertex of the quadratic function \(f(x) = a (x - h)2 + k\). Keep in mind that 'a' has the same value in both equations. Just set them equal so we can determine how the variables relate to one another.
To learn more about quadratic equation visit:
https://brainly.com/question/15816701
#SPJ4
consider the following word problem. What operation might we include if we were to create an expression? We bought 2 bags of takis for each child, z, and then gave away 1 bag of takis to a teacher
Answers
Answer:
2z-1 it think. jdjdjdjdjdjjdjd
SOMEONE PLEASE EXPLAIN THIS TO ME

Answers
P = 46.40°
Step-by-step explanation:
Since this is right triangle where all the sides are known we can use either sine, cosine or tangent of the angle to solve for P. Let use sine:
sin P = opp/hyp
= 21/29
or
P = arcsin(21/29) = arcsin(0.724)
= 46.40°
Complete the table to combine like terms when adding Expression One and Two.
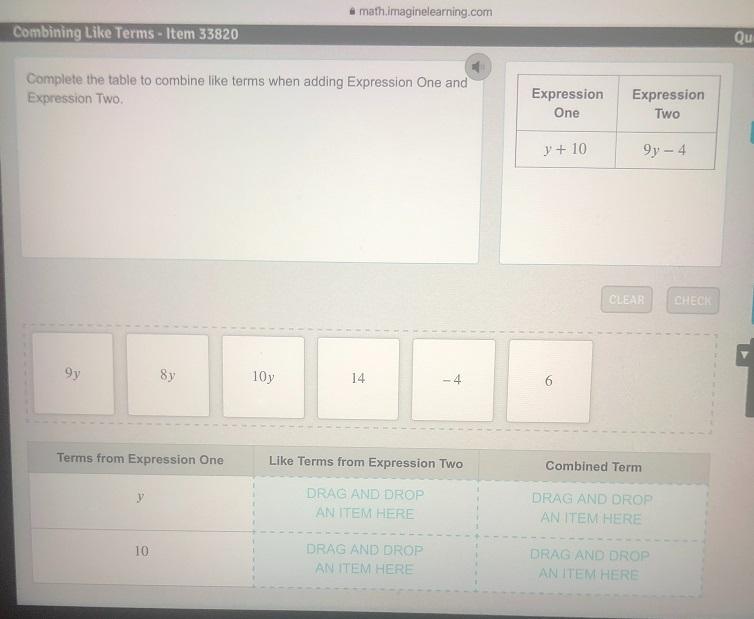
Answers
Answer:
10y+6
See diagram below
Explanation:
Given expressions One and Two below:
• Expression One: y+10
,• Expression Two: 9y-4
The completed table showing the addition of the expressions is given below:
Therefore:
\(\begin{gathered} y+9y=10y \\ 10-4=6 \\ \implies(y+10)+(9y-4)=10y+6 \end{gathered}\)The sum is 10y+6.

Please Help me on this, I'm a bit stuck on this one! Thanks if you do!

Answers
Answer:
z = 56
Step-by-step explanation:
124 and Z form a straight line so they will add to 180
124+z = 180
z = 180-124
z = 56
Answer:
z = 56°
Step-by-step explanation:
We know that vertically opposite angles are equal.
∴ y = 124°
We know that angles in a straight line are added up to 180°.
∴ y + z = 180
124 + z = 180
z = 180 - 124
z = 56°
x = 56° ( vertically opposite angles ⇒ x = z )
I need help
Solving this problem

Answers
The required value of x is 22 degrees for the given figure.
Adjacent angles are a sort of additional angle. Adjacent angles share a common side and vertex, such as a corner point. Their points do not overlap in any manner.
As we know that supplementary angles are defined as when pairing of angles addition to 180° then they are called supplementary angles.:
According to the given figure, it can be written as follows:
2x + 24 + 6x - 20 = 180
8x + 4 = 180
8x = 180 - 4
8x = 176
x = 176/8
x = 22
Therefore, the required value of x is 22 degrees for the given figure.
Learn more about supplementary angles here:
brainly.com/question/3027144
#SPJ1
The complete question is as follows:
Find the value of x for the below figure.

In Exercises 19–22, find the area of the parallelogram whose vertices are listed. 19. (0,0). (5.2), (6,4). (11.6) 20. (0,0). (-2.4). (6.-5). (4.-1) 21. (-2.0), (0, 3), (1.3). (-1.0)
Answers
The area of the parallelogram in exercise 19 is 6 square units. The area of the parallelogram in exercise 20 is 44.8 square units. The area of the parallelogram in exercise 21 is 5.9 square units.
19. To find the area of the parallelogram formed by the vertices (0,0), (5,2), (6,4), and (11,6), we can use the formula: Area = base × height. The base can be found as the distance between (0,0) and (5,2), which is √((5-0)^2 + (2-0)^2) = √29. The height can be found as the distance between (0,0) and (6,4), which is √((6-0)^2 + (4-0)^2) = √52. Thus, the area is √29 × √52 = √1508 = 6 square units.
20.To find the area of the parallelogram formed by the vertices (0,0), (-2,4), (6,-5), and (4,-1), we can again use the formula: Area = base × height. The base can be found as the distance between (0,0) and (6,-5), which is √((6-0)^2 + (-5-0)^2) = √61. The height can be found as the distance between (0,0) and (4,-1), which is √((4-0)^2 + (-1-0)^2) = √17. Thus, the area is √61 × √17 = √1037 = 44.8 square units.
21.To find the area of the parallelogram formed by the vertices (-2,0), (0,3), (1,3), and (-1,0), we can once again use the formula: Area = base × height. The base can be found as the distance between (-2,0) and (1,3), which is √((-2-1)^2 + (0-3)^2) = √18. The height can be found as the distance between (-2,0) and (-1,0), which is 1 unit. Thus, the area is √18 × 1 = √18 = 5.9 square units.
To learn more about parallelogram.
Click here:brainly.com/question/28854514?
#SPJ11
Graph a line with a slope of 2/5 that contains the point(-2,4)
So...(-2,4) and ( ?, ?) =
Please Help!!!!
Will Mark Brainliest!!!!!
Answers
Answer:
(-2, 4) (3, 6)
Step-by-step explanation:
I think this would be correct? haha
y2-y1/x2-x1
6-4=2,3--2(or 3+2 because 2 negatives make a positive)=5, so 2/5.
I hope this helps :)
PLEASE HELP ASAP‼️Solve the triangle MNO (find m
m and n).
n =
M
34°
12 cm
m=
N
4

Answers
First, we can find m by using the following formula:
sin(m)/12 = sin(34)/4
Solving for m, we get:
m = sin^-1(12sin(34)/4) ≈ 56.4°
Next, we can find n by using the law of sines again:
sin(n)/12 = sin(180-34-m)/sin(34)
Solving for n, we get:
n = sin^-1(12sin(112)/sin(34)) ≈ 87.6°
Therefore, m ≈ 56.4° and n ≈ 87.6°.
how many terms are in the following expression?
Answers
The number of terms in the expression, 6 + 2 x - 4 y + 5 z is 4 terms.
How to find the number of terms ?In the expression 6 + 2x - 4y + 5z, the number of terms is four, not the number of signs. The terms in this expression are:
62 x- 4 y 5 zEach term is separated by an operator (either addition or subtraction), which is represented by a sign. Therefore, the expression contains three addition signs and one subtraction sign.
Find out more on the number of terms at https://brainly.com/question/30659621
#SPJ1
The full question is:
How many terms are in the following expression 6 + 2 x - 4 y + 5 z