Please help me out!!! :)
How can you look at the equation of two lines and determine if they will be parallel?
Answers
Answer:
fafg and then do the 2a ab 2b
Step-by-step explanation:
Related Questions
What is the cardinality of the set {2, {3}}?
Answers
Given,
The set is {2, {3}}.
The cardinity of the set is the number of elements in the set.
Consider,
A = {2, {3} }
The cardinity of the set is,
\(|A|=2\)Hence, the cardinality of the set is 2.
Can someone help me with that problem plz
13. Determine which concept differs from the others. (pick the correct answer)
(a) x-intercept
(b) intercept
(c) roots
(d) zeros
Answers
( x-intercept roots and zeros are all names that make something equal to 0)
HELP ME PLSSS. ANSWER NEEDS TO BE EXPLAIN STEP BYE STEPS.CORRECT ANSWER WILL BE BRAINLIST.


Answers
Solution given.
Volume of rectangular prism=2400cm³
area of base*height=2400cm³
For A
satisfied for all
for B
not satisfied for all
for C
not satisfied for all
for D.
not satisfied for all
Option A.is your answer.
If m
15 points thanks you :)


Answers
Answer:
48
Step-by-step explanation:
check the attached file

according to the logic of inferential statistics, before an independent variable has been administered, means from each group in the study are assumed to be:
Answers
In inferential statistics, before administering an independent variable, means from each group in the study are assumed to be equal or similar.
In inferential statistics, researchers often compare groups to determine whether there are significant differences between them. Before administering an independent variable, which is a variable that is manipulated by the researcher, it is generally assumed that the means of each group are equal or similar. This assumption allows for a fair and unbiased comparison between groups. By assuming equal means, researchers can then analyze the data using statistical tests to determine if there are significant differences between the groups after administering the independent variable.
The assumption of equal means serves as a starting point for hypothesis testing and helps researchers assess the impact of the independent variable on the dependent variable. If there were already significant differences in means before administering the independent variable, it would be difficult to attribute any observed differences solely to the independent variable. Therefore, assuming equal means before the manipulation of the independent variable ensures that any subsequent differences can be more confidently attributed to the variable being tested. This assumption allows researchers to draw valid conclusions and make informed decisions based on the results of their statistical analyses.
Learn more about means here: https://brainly.com/question/28830856
#SPJ11
Help please if you don’t mind!!
Thankyou so much

Answers
Answer:
Step-by-step explanation:
\(F = \frac{9}{5}C+32\)
Subtract 32 from both sides
\(F-32= \frac{9}{5}C\\\)
Multiply both side by 5/9
\(\frac{5}{9}(F-32)=( \frac{5}{9})* \frac{9}{5}C\\\\ \frac{5}{9}(F-32)=C\\\)
F= 41
\(\frac{5(41-32)}{9}=C\\\\ \frac{5*9}{9}=C\\\\ \frac{45}{9}=C\\\\C = 5\\\\\)
41° F = 5° C
\( {75}^{2} + 25 - 750\)
Answers
A rectangle has an area of 42 ft. Suppose that the width and length of the rectangle are changing, while the area stays fixed. If the length is increasing at a rate of 2 ft/s, what is the rate of change of the width with respect to time when the length is 6 ft?
Answers
The rate of change of the width with respect to time when the length is 6 ft is -7 ft/s.
How does the rate of change of the width with respect to time vary when the length of the rectangle is fixed at 6 ft?
When the area of a rectangle remains constant, changes in its dimensions affect the rates of change of its length and width. Let's denote the width of the rectangle as w and the length as l. We know that the area (A) is given by the formula A = l * w. Since the area is fixed at 42 ft², we have the equation 42 = 6w, which implies w = 7 ft. Now, we can differentiate both sides of the equation with respect to time (t) to find the rates of change. dA/dt = (dl/dt) * w + l * (dw/dt). Given that dl/dt = 2 ft/s, l = 6 ft, and w = 7 ft, we can solve for dw/dt. Substituting the known values into the equation, we have 0 = 2 * 7 + 6 * (dw/dt), which simplifies to dw/dt = -7 ft/s. Therefore, the rate of change of the width with respect to time when the length is 6 ft is -7 ft/s.
Calculus and its applications in various real-life scenarios, such as determining rates of change and optimizing quantities, in order to solve problems involving dynamic systems and relationships between variables. Understanding calculus can enable you to analyze and predict how variables interact and change over time, making it a powerful tool in fields like physics, engineering, economics, and more. By delving deeper into the concepts and techniques of calculus, you can enhance your problem-solving skills and gain a better understanding of the world around you.
Learn more about Equation
brainly.com/question/13763238
#SPJ11
Help help help please math

Answers
Answer:
115,571,923,290.8
this is the answer will u mark me as brainlist
if f(1) = 12, f ' is continuous, and 6 f '(x) dx 1 = 16, what is the value of f(6)
Answers
To find the value of f(6), we can use the information given about the function f(x) and its derivative f'(x).The value of f(6) is 44/3.
Given that f'(x) is continuous, we can apply the Fundamental Theorem of Calculus. According to the theorem:
∫[a to b] f '(x) dx = f(b) - f(a)
In this case, we are given that:
∫[1 to 6] 6 f '(x) dx = 16
We can simplify the integral:
6 ∫[1 to 6] f '(x) dx = 16
Since f'(x) is the derivative of f(x), the integral of 6 f '(x) dx is equal to 6 f(x). Therefore, we have:
6 f(6) - 6 f(1) = 16
Substituting the given value f(1) = 12:
6 f(6) - 6(12) = 16
6 f(6) - 72 = 16
Next, we isolate the term with f(6):
6 f(6) = 16 + 72
6 f(6) = 88
Finally, we solve for f(6) by dividing both sides by 6:
f(6) = 88 / 6
f(6) = 44/3
To learn more about derivate click here:
brainly.com/question/31769642
#SPJ11
Corie buys dog food in a 34-pound bag. Her dog eats about 1 pound a day. Corie buys cat
food in a 16-pound bag. Her cat eats about 1/4 pound a day. Assume she buys new bags of pet
food on the same day. On which day will the two bags have the same weight? Show how you
figured it out.
Answers
The day the two bags will have the same weight is the 24th day.
On which day will the two bags have the same weight?The linear equation that can be used to determine the pound of dog food left is:
Amount of dog food left = capacity of the bag - (number of days x amount the dog eats per day)
Amount of dog food left = 34 - (1 x p)
Amount of dog food left = 34 - 1p
The linear equation that can be used to determine the pound of cat food left is:
Amount of cat food left = capacity of the bag - (number of days x amount the cat eats per day)
Amount of cat food left = 16 - (1/4 x p)
Amount of cat food left = 16 - 1/4p
On the day the two bags will have the same weight, the two above equations would be equal:
16 - 1/4p = 34 - 1p
p - 1/4p = 34 - 16
3/4p = 18
p = (18 x 4) / 3
p = 24 days
To learn more about linear equations, please check: https://brainly.com/question/25711114
#SPJ1
Erik used the Factor Theorem to find the remainder of 2x3-4x2-28x+6 divided by x+3. If he calculated the remainder to be 0, what does that tell him?
Answers
Step-by-step explanation:
x + 3 = 0
x = - 3
f(x) = 2x³ - 4x² - 28x + 6
f(- 3) = 2(- 3)³ - 4(- 3)² - 28 x (- 3) + 6
= 2 x (- 27) - (4 x 9) + 84 + 6
= - 54 - 36 + 90
= - 90 + 90
= 0
Therefore,
x + 3 is factor of 2x³ - 4x² - 28x + 6
PLS HELP ASAP!! WORTH 30 POINT,PLS TRY TO BE ORGANIZED AND IF U CAN MAYBE DO IT ON PAPER SO ITS EASIER LIKE JS SOLVE IT ON PAPER W/O NO EXPLANATION OR ON HERE W EXPLANATION.SHOW UR WORK PLS SOLVE INEQUALITIES WITH INTEGERS, Q:#12-#15 THANK UU(:

Answers
The range of x are;
1. x < -30
2. x > 8
3. x > 15
4. x < -2
What is inequality?A relationship between two expressions or values that are not equal to each other is called 'inequality.
1. -130 > 50x +20
-130-20> 50x
-150 > 50x
-150/50 > x
-30 > x
x < -30
2. -8(x-3) < -40
-8x +24< -40
collect like terms
-8x < -64
x > -64/-8
x > 8
3. 2x - 22 > 8
collect like terms
2x > 30
divide both sides by 2
x > 30/2
x > 15
4. -35 < -5(x+9)
-35 < -5x -45
collect like terms
10 < -5x
-2 > x
x < -2
learn more about inequality from
https://brainly.com/question/24372553
#SPJ1
Find the smallest value of k, such that 16k is a perfect cube.
Answers
Answer:
k = 4
Step-by-step explanation:
16k = 16(4) = 64 and
64 = 4 × 4 × 4
\(\sqrt[3]{64}\)
= \(\sqrt[3]{4^{3} }\)
= 4
PLEASE THIS IS URGENTTT
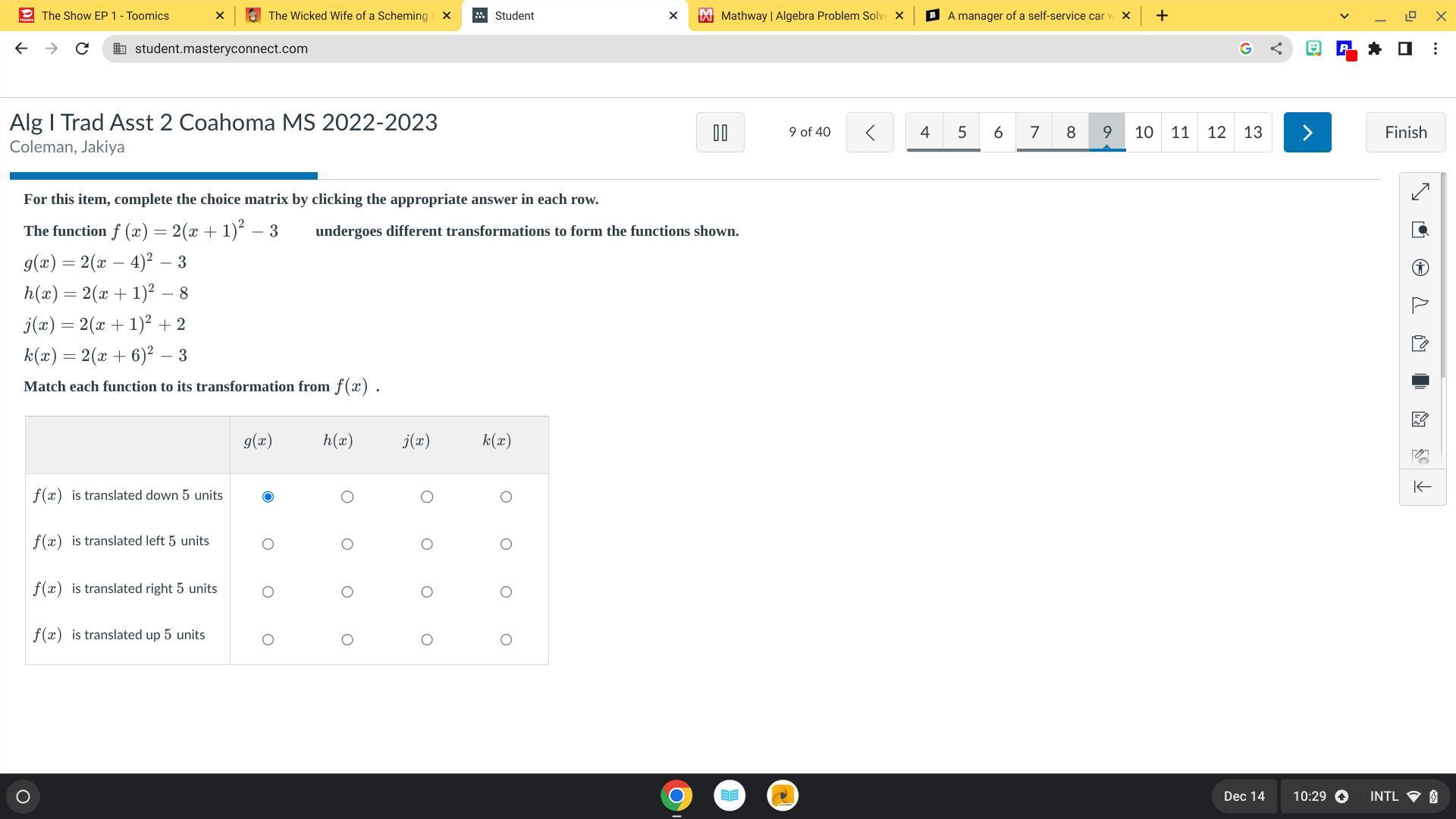
Answers
The functions and their transformations are
h(x) = 2(x + 1)² - 8: a translation down by 5 unitsk(x) = 2(x + 6)² - 3: a translation left by 5 units g(x) = 2(x - 4)² - 3: a translation right by 5 unitsj(x) = 2(x + 1)² + 2: a translation up by 5 unitsHow to match the functions and the transformations?From the question, we have the following parameters that can be used in our computation:
f(x) = 2(x + 1)² - 3
A translation down by 5 units is represented as
f(x) - 5
So, we have
f(x) - 5 = 2(x + 1)² - 3 - 5
f(x) - 5 = 2(x + 1)² - 8
Rewrite as
h(x) = 2(x + 1)² - 8
A translation left by 5 units is represented as
f(x + 5)
So, we have
f(x + 5) = 2(x + 1 + 5)² - 3
f(x + 5) = 2(x + 6)² - 3
Rewrite as
k(x) = 2(x + 6)² - 3
A translation right by 5 units is represented as
f(x - 5)
So, we have
f(x - 5) = 2(x + 1 - 5)² - 3
f(x - 5) = 2(x - 4)² - 3
Rewrite as
g(x) = 2(x - 4)² - 3
A translation up by 5 units is represented as
f(x) + 5
So, we have
f(x) + 5 = 2(x + 1)² - 3 + 5
f(x) + 5 = 2(x + 1)² + 2
Rewrite as
j(x) = 2(x + 1)² + 2
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
17) Eli packed 1,920 peanuts into 8 sacks. He packed an equal number of peanuts in each sack. How many peanuts did he pack into each sack?
Answers
Answer:
240
Step-by-step explanation:
you have to divide 1,920 by 8
what is mean arterial pressure formula
Answers
The mean arterial pressure formula is MAP = CO x TPR or MAP = (SBP + 2DBP) / 3.
The mean arterial pressure (MAP) formula is:
MAP = CO x TPR
where:
CO is the cardiac output (how much blood is siphoned by the heart each moment)
TPR is the all-out peripheral resistance (the resistance from the bloodstream in the body's veins)
On the other hand, the mean arterial pressure can also be calculated using the following equation:
MAP = (SBP + 2DBP)/3
where:
SBP is the systolic blood pressure (the highest pressure in the arteries when the heart beats)
DBP is the diastolic blood pressure(the lowest pressure in the arteries when the heart is at rest between beats)
Learn more about mean arterial pressure:
https://brainly.com/question/13209101
#SPJ4
Write an equation of the line in slope-intercept form
Y= ?

Answers
Answer:
y=-7x+4
Hope it helps!
In 2012, gallup asked participants if they had exercised more than 30 minutes a day for three days out of the week. Suppose that random samples of 100 respondents were selected from both vermont and hawaii. From the survey, vermont had 65. 3% who said yes and hawaii had 62. 2% who said yes. What is the value of the sample proportion of people from vermont who exercised for at least 30 minutes a day 3 days a week?.
Answers
The value of the sample proportion of people from Vermont who exercised for at least 30 minutes a day 3 days a week is 0.653, which is equivalent to 65.3%.
It is important to note that this value is based on a random sample of respondents and may not necessarily represent the true proportion of the entire population of Vermont who exercise regularly.
To find the sample proportion of people from Vermont who exercised for at least 30 minutes a day, 3 days a week, follow these steps:
1. Convert the given percentage (65.3%) to a decimal by dividing by 100: 65.3 / 100 = 0.653
2. Multiply the decimal by the number of participants in the random sample (100 respondents): 0.653 * 100 = 65.3
3. Round the result to the nearest whole number to find the number of participants who exercised: 65.3 ≈ 65
4. Divide the number of participants who exercised (65) by the total number of participants in the random sample (100): 65 / 100 = 0.65
This means that out of the 100 participants sampled from Vermont, 65.3 of them answered "yes" to the question of whether they had exercised for more than 30 minutes a day for three days out of the week.
The value of the sample proportion of people from Vermont who exercised for at least 30 minutes a day, 3 days a week is 0.65 or 65%.
Learn more about sample proportion here:
brainly.com/question/29912751
#SPJ11
What is the shape of the distribution of the number of siblings? skewed to the left bimodal symmetric skewed to the right unimodal symmetric
Answers
The shape of the distribution of the number of siblings can vary depending on the specific data set.
However, if we are considering the general case, the most common shape of the distribution is likely to be unimodal and skewed to the right.
This means that the majority of individuals are likely to have fewer siblings,
and as the number of siblings increases,
the frequency of individuals with that number decreases.
The distribution may also have a long tail on the right side,
indicating a few individuals with a significantly larger number of siblings.
However, it is important to note that this is just a general observation, and in specific cases,
the distribution may be different.
To know more about distribution visit:
https://brainly.com/question/33255942
#SPJ11
pls help asap!! will give brainliest

Answers
Answer:
i believe the answer is A 90
Step-by-step explanation:
How do you find the surface area of a cube if one side measures 10cm? show your solution.
Answers
Answer:
600 cm squared :)
Step-by-step explanation:
Surface area of cube: 6 x s^2
Now lets solve!!
6 x 10^2
6 x 100
600
Have an amazing day!!
Please rate and mark brainliest!!
Find the perimeter and area of the figure. Round to the nearest tenth if necessary.
*
2 points

Answers
Answer: D
Step-by-step explanation:
\(A=\frac{1}{2}bh\\\\A=\frac{1}{2}(4.8)(7.2)\\\\A \approx \boxed{17.3}\)
2k-3/5k-6 = 2/3 what does k equal to
Answers
Answer:
100/21
Step-by-step explanation:
Steps to solve
3(2k - 3) = 2(5k - 6)
6k - 9 = 10k - 12
6k - 10k = -12 + 9
-4k = -3
k = 3/4
A moving company drove one of its trucks 100,042 miles one year. A second truck was driven 98,117 miles, and a third truck was driven 120,890 miles. How many miles were driven by all three trucks?
Answers
How do you show that f and G are inverses of each other?
Answers
First make the graph of the functions, then if the two graphs are symmetric with respect to the line y = x (mirror images over y = x ), then they are inverse functions.
Symmetric
A figure or shape that can be divided into two equal parts by a line is called symmetric figures.
Inverse Functions
The inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by F^-1.
Learn more about graph and functions here :-
brainly.com/question/17267403
#SPJ4
What value of x makes this equation true?
12x -15 = 6 -3x
Answers
Answer:
1.4
Step-by-step explanation:
12x-15=6-3x
+3x +3x
15x-15=6
+15 +15
15x=21
/15. /15
x=1.4
hopes this helps
Answer:
1.4
Step-by-step explanation:
12x-15+3x=6
15x-15=6
15x=6+15
15x=21
x=21:15
x=1.4
Consider a continuous-time Markov chain with three states 1, 2, 3, 4, 5 and transition rates q12=1, q13 = 2, q21 = 0, q23 = 3, q31 = 0, q32 = 0. (1) Write the system of ODEs for the corresponding transition probabilities Pᵢⱼ (t) . (2) Suppose that the initial state is 1. What is the probability that after the first transition, the process X(t) enters state 2?
Answers
the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
To write the system of ordinary differential equations (ODEs) for the transition probabilities Pᵢⱼ(t) of the given continuous-time Markov chain, we need to consider the rate at which the system transitions between different states.
Let Pᵢⱼ(t) represent the probability that the Markov chain is in state j at time t, given that it started in state i at time 0.
The ODEs for the transition probabilities can be written as follows:
dP₁₂(t)/dt = q₁₂ * P₁(t) - q₂₁ * P₂(t)
dP₁₃(t)/dt = q₁₃ * P₁(t) - q₃₁ * P₃(t)
dP₂₁(t)/dt = q₂₁ * P₂(t) - q₁₂ * P₁(t)
dP₂₃(t)/dt = q₂₃ * P₂(t) - q₃₂ * P₃(t)
dP₃₁(t)/dt = q₃₁ * P₃(t) - q₁₃ * P₁(t)
dP₃₂(t)/dt = q₃₂ * P₃(t) - q₂₃ * P₂(t)
where P₁(t), P₂(t), and P₃(t) represent the probabilities of being in states 1, 2, and 3 at time t, respectively.
Now, let's consider the second part of the question: Suppose that the initial state is 1. We want to find the probability that after the first transition, the process X(t) enters state 2.
To calculate this probability, we need to find the transition rate from state 1 to state 2 (q₁₂) and normalize it by the total rate of leaving state 1.
The total rate of leaving state 1 can be calculated as the sum of the rates to transition from state 1 to other states:
total_rate = q₁₂ + q₁₃
Therefore, the probability of transitioning from state 1 to state 2 after the first transition can be calculated as:
P(X(t) enters state 2 after the first transition | X(0) = 1) = q₁₂ / total_rate
In this case, the transition rate q₁₂ is 1, and the total rate q₁₂ + q₁₃ is 1 + 2 = 3.
Therefore, the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
Learn more about probability here
https://brainly.com/question/32117953
#SPJ4
Find the Laplace transform of the following functions. 3. f(t) = 3sinht + 5cosht 4. f(t) = 4e-6 + 3sin2t +9 = -6
Answers
The Laplace transform of the following functions are:
1. f(t) = 3sinht + 5cosht
To find the Laplace transform of f(t) = 3sinht + 5cosht,
use the following formula:
\($$\mathcal{L}\{f(t)\} = \frac{s}{s^{2} + a^{2}} $$\)
Where a is a constant. Let a = 1.
\($$ \begin{aligned} \mathcal{L}\{f(t)\} &= \mathcal{L}\{3sinht + 5cosht\} \\ &= 3\mathcal{L}\{sinht\} + 5\mathcal{L}\{cosht\} \\ &= 3\left(\frac{1}{s-1} \right) + 5\left(\frac{s}{s^{2} + 1^{2}} \right) \\ &= \frac{3}{s-1} + \frac{5s}{s^{2} + 1} \end{aligned} $$\)
Therefore, the Laplace transform of f(t) = 3sinht + 5cosht is
\($$\mathcal{L}\{f(t)\} = \frac{3}{s-1} + \frac{5s}{s^{2} + 1} $$\)
2. f(t) = 4e-6 + 3sin2t +9 = -6
To find the Laplace transform of f(t) = 4\(e^-6\)+ 3sin2t +9 = -6,
use the following formula:
\($$\mathcal{L}\{f(t)\} = \mathcal{L}\{4e^{-6} + 3sin2t -6 \} $$\)
Taking Laplace transform of each term, we get
\($$ \begin{aligned} \mathcal{L}\{4e^{-6} + 3sin2t -6 \} &= \mathcal{L}\{4e^{-6}\} + \mathcal{L}\{3sin2t\} - \mathcal{L}\{6\} \\ &= 4\mathcal{L}\{e^{-6}\} + 3\mathcal{L}\{sin2t\} - 6\mathcal{L}\{1\} \\ &= 4\left(\frac{1}{s+6}\right) + 3\left(\frac{2}{s^{2} + 2^{2}}\right) - 6\left(\frac{1}{s}\right) \\ &= \frac{4}{s+6} + \frac{6}{s^{2} + 4} - \frac{6}{s} \end{aligned} $$\)
Therefore, the Laplace transform of f(t) = 4\(e^-6\) + 3sin2t +9 = -6 is
\($$\mathcal{L}\{f(t)\} = \frac{4}{s+6} + \frac{6}{s^{2} + 4} - \frac{6}{s} $$\)
To know more about Laplace transform visit:
https://brainly.com/question/30759963
#SPJ11
The Laplace Transform of a function f(t) is defined as F(s) = L{f(t)}.
Find the Laplace transform of the following functions below.
3. f(t) = 3sinht + 5cosht
Using the following Laplace transforms:
L{sinh(at)} = a / \((s^2-a^2)\),
L{cosh(at)} = s / \((s^2-a^2)\), and
L{a cosh(at)} = s / \((s^2-a^2)\)
where a is a constant,
we can find the Laplace transform of the given function f(t) = 3sinht + 5cosht.
L{3sinht + 5cosht} = 3 L{sinh(t)} + 5 L{cosh(t)}
Substituting the Laplace transforms:
\(3 * [a / (s^2-a^2)] + 5 * [s / (s^2-a^2)] = [3a + 5s] / (s^2-a^2)\)
Therefore, the Laplace transform of the function f(t) = 3sinht + 5cosht is F(s) = [3a + 5s] /\((s^2-a^2)\).4.
f(t) = \(4e^{(-6t)\)+ 3sin(2t) + 9
Using the Laplace transform of the unit step function, \(L{e^{-at} u(t)} = 1 / (s+a)\), and
the Laplace transform of sin(at), L{sin(at)} = a / \((s^2 + a^2)\),
we can find the Laplace transform of the given function f(t) =\(4e^{(-6t)\) + 3sin(2t) + 9.
L{\(4e^{(-6t)\) + 3sin(2t) + 9}
= 4L{\(e^{(-6t)\) u(t)} + 3L{sin(2t)} + 9L{1}
Substituting the Laplace transforms:
4 * [1 / (s+6)] + 3 * [2 / (\(s^2\) + 4)] + 9 * [1 / s] = [36\(s^2\) + 78s + 76] / [(s+6)(\(s^2\) + 4)]
Therefore, the Laplace transform of the function f(t) = \(4e^{(-6t)\) + 3sin(2t) + 9 is F(s) = [36\(s^2\) + 78s + 76] / [(s+6)(\(s^2\) + 4)].
To know more about Laplace transform visit:
https://brainly.com/question/14487937
#SPJ11
Put your answer as a reduced fraction.
Solve.
y/-8 = 1/16
y =
Answers
Hey there!☺
\(Answer:\boxed{y=\frac{-1}{2}}\)
\(Explanation:\)
\(\frac{y}{-8}=\frac{1}{16}\)
In our first step, we will use the cross multiply method:
\(\frac{y}{-8}=\frac{1}{16}\\ y*(16)=(1)*(-8)\\16y=-8\)
In our second/last step, we will divide both sides by 16:
\(\frac{16y}{16}=\frac{-8}{16}\\y=\frac{-1}{2}\)
Hope this helps!☺
Answer:
Step-by-step explanation:
16y = -8
y = -8/16
y = -1/2