Answers
Answer:
in = - 9.5
Step-by-step explanation:
- 9.5 × 2 = -19
-19 - 1 = -20
Related Questions
find the square root of 7921 ?
Answers
Answer:
±89
Step-by-step explanation:
..................
What is the solution to the system of equations y =- 3x 2 5x 2y 15?
Answers
The solution for the system of equations is (-19,55).
As given the equations in the question
y = –3x – 2
Simplify the above
y + 3x = -2
5x + 2y = 15
Multiply y + 3x = -2 by 2 and subtracted from 5x + 2y = 15.
2y - 2y + 5x -6x = 15 + 4
-x = 19
x = -19
Putting the value of x in the equation y + 3x = -2.
y + 3 × - 19 = -2
y - 57 = -2
y = -2 + 57
y = 55
Therefore the solution for a system of equations is (-19,55).
To Know more about the system of equations:
https://brainly.com/question/2002446
#SPJ4
Solve the equation: 1/3 x - 4 = 28
Answers
Answer:
x = 96
Step-by-step explanation:
Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
First, add 4 to both sides:
(1/3)x - 4 (+4) = 28 (+4)
(1/3)x = 28 + 4
(1/3)x = 32
Next, multiply 3 to both sides:
(3)(1/3)x = (32)(3)
x = 32 * 3
x = 96
x = 96 is your answer.
~
Answer:
96=x
Step-by-step explanation:
Add 4 to each side
1/3x= 32
multiply 3 on each side to cancel out the fraction
x=96
If who answers fast, correct and first, I WILL GIVE YOU THE BRAINLIEST!!!!!!!!!!!

Answers
41+71=112
180-112=68
Angle of BAC=68 degrees
Question 2 options: A population of bacteria doubles every 15 hours. Initially, the population of bacteria is 50. What is the population of the bacteria after 40 hours
Answers
After 40 hours the population of bacteria will be equals to 318 hours.
We can calculate the total population growth using the following equation:
A(t)= A₀× 2ᵗ/¹⁵
Where, A(t) --> the total population
A₀ --> the initial population
t --> the time in hours
From the statement we know that the population of bacterias doubles every 15 hours, so, using the formula we have: A(15) = A₀ × 2ᵗ/¹⁵
The initial population is = 50 , then
A(15) = 50×2¹⁵/¹⁵ = 100
It shows that every 15 hours, the population of bacterias doubles it size. We are asked to calculate the popualation after 40 hours, so:
A(40) = 50 × 2⁴⁰/¹⁵
= 6.35 × 50 = 317.5 ~ 318
So, after 40hours the population of bacteria will be 318.
To learn more about population growth, refer:
https://brainly.com/question/27779235
#SPJ4
How does T critical value calculator work?
Answers
The working of T critical value calculator is explained
What is t test?
t test is the test used if the sample standard deviation is known and population standard deviation is unknown.
t test is used if the sample standard deviation is known and population standard deviation is unknown.
Here, t value is calculated by the formula
\(t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}\)
\(\bar{x}\) = mean of the sample
\(\mu\) = mean of the population
s = standard deviation of sample
n = Number of samples
Now, with the help of degree of freedom (n - 1) and the level of significance, the critical value of t is to be noted from the t table. Let it be \(t_{critical}\)
if the value of t lies between \(-t_{critical}\) and \(+t_{critical}\) then the null hypothesis is accepted, otherwise the null hypothesis is rejected.
To learn more about t test, refer to the link
https://brainly.com/question/6589776
#SPJ4
If z is directly proportional to the product of x and y and if z is 10 when x is 4 and y is 5, then x, y, and z are related by the equation
Answers
The equation relating x, y, and z is:
z = 0.5 * x * y.
In the given problem, the relationship between x, y, and z can be expressed by the equation z = k * x * y, where k represents the constant of proportionality. By substituting the values of x = 4 and y = 5, when z is equal to 10, we can determine the value of the constant of proportionality, k, and further define the relationship between the variables.
To find the constant of proportionality, we substitute the known values of x = 4, y = 5, and z = 10 into the equation z = k * x * y. This gives us the equation 10 = k * 4 * 5. By simplifying the equation, we have 10 = 20k. To isolate k, we divide both sides of the equation by 20, resulting in k = 0.5. Therefore, the equation relating x, y, and z is z = 0.5 * x * y, meaning that z is directly proportional to the product of x and y with a constant of proportionality equal to 0.5.
To learn more about proportionality, click here: brainly.com/question/28194586
#SPJ11
1. Find the slope of a line given the points
below.
(2,8) and (8,20)
Answers
Answer:
Slope is 2
Step-by-step explanation:
To find slope
m=y2-y1
---------
x2-x1
m= 20-8
------
8-2
m= 12
---
6
m=2
Answer:
m=2
Step-by-step explanation:
What is this slope of the line on the graph?

Answers
Answer:
Step-by-step explanation:
m = 5/7 is the slope of the line on the graph .
What is slope in plain ?
A line or a part of a line that connects two locations is said to have a slope, which is a measure of how steep it is.
The ratio of how much y grows as x grows by a certain amount is known as a line's slope. The slope of a line indicates how steep it is, or how much y rises as x rises.
The slope-intercept form of an equation is used whenever the equation of a line is expressed in the form y = mx + b.
point from given graph x = ( -7 , 0 ) and y = ( 0, 5 )
slope (m) =
m =
m = 5/7
Learn more about slope
brainly.com/question/3605446
here you go im late tho...
Which equation represents a line that passes through (5, 1) and has a slope of StartFraction one-half EndFraction?
y – 5 = y minus 5 equals StartFraction one-half EndFraction left-parenthesis x minus 1 right-parenthesis.(x –1)
y – y minus StartFraction one-half EndFraction equals 5 left-parenthesis x minus 1 right-parenthesis. = 5(x –1)
y – 1 = y minus 1 equals StartFraction one-half EndFraction left-parenthesis x minus 5 right-parenthesis.(x –5)
y – 1 = 5y minus 1 equals 5 left-parenthesis x minus StartFraction one-half EndFraction right-parenthesis
Answers
Answer:
y - 1 = 1/2(x -5)
Just took the test, hope this helps!
Answer:
above is correct the letter answer is C on edg2020
Step-by-step explanation:
edg2020
PLEASE HELP THANK YOU
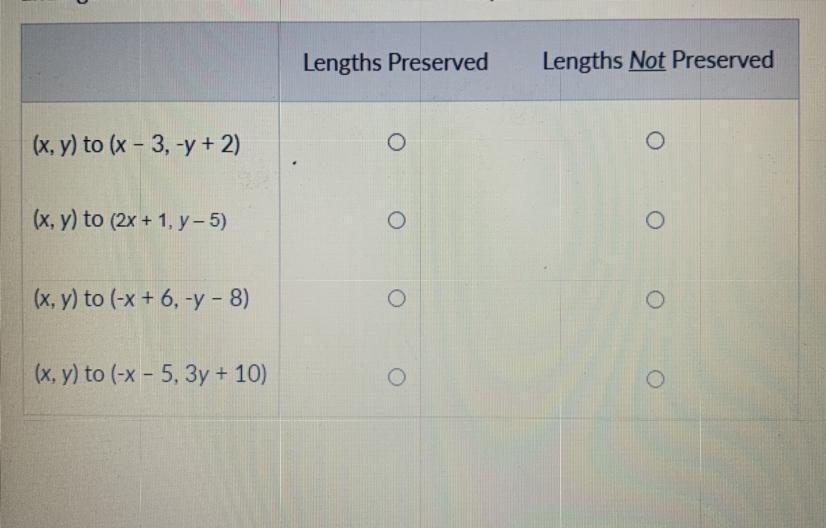
Answers
Hope this helps. :D
The number of patients treated at Dr. Frank's dentist office each day was recorded for ten days: 13, 9, 7, 8, 2, 4, 22, 12, 5, 0. Using the given data, find the mean for this sample.
Answers
The mean of the sample from number of patients treated at Dr. Frank's dentist office each day for ten days is 8.2
MeanGiven data:
13, 9, 7, 8, 2, 4, 22, 12, 5, 0.
Mean of the sample = Total number of patients treated / number of days
= (13 + 9 + 7 + 8 + 2 + 4 + 22 + 12 + 5 + 0) / 10
= 82/10
= 8.2
Therefore, the mean of the sample is 8.2
Learn more about mean:
https://brainly.com/question/14532771
#SPJ1
Solve for v.
–5v = 3v − 16
Answers
。☆✼★ ━━━━━━━━━━━━━━ ☾
-5v = 3v - 16
- 3v
-8v = -16
/ -8
v = 2
Have A Nice Day ❤
Stay Brainly! ヅ
- Ally ✧
。☆✼★ ━━━━━━━━━━━━━━ ☾
Answer:
v = 2
Step-by-step explanation:
-5v = 3v - 16
- 3v
-8v = -16
/ -8
v = 2
Thirty years ago, Peter was gifted a $100 savings deposit that pays 5% anneally from his grandmother. Approximately what is its Worthnow?
$150
$300
$432.
$332
Answers
The approximate worth of Peter's $100 savings deposit after 30 years with a 5% annual interest rate is $432.
The approximate worth of Peter's $100 savings deposit after 30 years with a 5% annual interest rate is $432. The formula that can be used to calculate the future value of a deposit with simple interest is: FV = PV(1 + rt), where FV is the future value, PV is the present value, r is the interest rate, and t is the time in years.
Using this formula, we can calculate the future value as FV = 100(1 + 0.05 * 30) = $250. However, this calculation is based on simple interest, and it does not take into account the compounding of interest over time.
To calculate the future value with compounded interest, we can use the formula: FV = PV(1 + r)^t. Plugging in the given values, we get FV = 100(1 + 0.05)^30 = $432.05 approximately.
Therefore, the approximate worth of Peter's $100 savings deposit after 30 years with a 5% annual interest rate is $432.
Know more about simple interest here:
https://brainly.com/question/30964674
#SPJ11
3. Graph the rational function x2 - 3/x-1 . Both branches of the rational function y= = X-1 pass through which quadrant? Quadrant 1 Quadrant 3 Quadrant 2 Ouadrant 4
Answers
To graph the rational function y = (x^2 - 3)/(x - 1), we need to first find its vertical and horizontal asymptotes, intercepts, and critical points.
Intercepts:
To find the x-intercept, we set y = 0 and solve for x:
0 = (x^2 - 3)/(x - 1)
0 = x^2 - 3
x = ±√3
So the x-intercepts are (±√3, 0).
To find the y-intercept, we set x = 0:
y = (0^2 - 3)/(0 - 1) = 3
So the y-intercept is (0, 3).
Critical points:
To find the critical points, we take the derivative of the function and set it equal to zero:
y = (x^2 - 3)/(x - 1)
y' = [(2x)(x - 1) - (x^2 - 3)]/(x - 1)^2
y' = (x^2 - 2x - 3)/(x - 1)^2
0 = (x^2 - 2x - 3)/(x - 1)^2
0 = x^2 - 2x - 3
x = 1 ± √4
x = 3, -1
So the critical points are (3, 0) and (-1, 0).
- Plot the vertical asymptote at x = 1.
- Plot the horizontal asymptote at y = x.
- Plot the x-intercepts at (±√3, 0).
- Plot the y-intercept at (0, 3).
- Plot the critical points at (3, 0) and (-1, 0).
- To determine which quadrants the branches of the function pass through, we can test a point in each quadrant. For example, if we plug in x = 2 (which is in quadrant 1) into the function, we get y = -1/2, which is negative. If we plug in x = -2 (which is in quadrant 2) into the function, we get y = 5/3, which is positive. So the upper branch of the function passes through quadrant 2 and the lower branch passes through quadrant 4.
1. Vertical asymptote: Set the denominator (x - 1) equal to 0 and solve for x:
x - 1 = 0
x = 1
2. Horizontal asymptote: Compare the degrees of the numerator and denominator:
Degree of the numerator (x^2) = 2
Degree of the denominator (x - 1) = 1
Since the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
3. X-intercept: Set y = 0 and solve for x:
(x^2 - 3) / (x - 1) = 0
x^2 - 3 = 0
x = ±√3
4. Y-intercept: Set x = 0 and solve for y:
y = (0^2 - 3) / (0 - 1)
y = -3
Now, we can determine in which quadrants both branches of the rational function pass through.
- Quadrant 1: x > 0 and y > 0
- Quadrant 2: x < 0 and y > 0
- Quadrant 3: x < 0 and y < 0
- Quadrant 4: x > 0 and y < 0
To know more about horizontal asymptotes visit :-
https://brainly.com/question/4084552
#SPJ11
Does anyone know?????
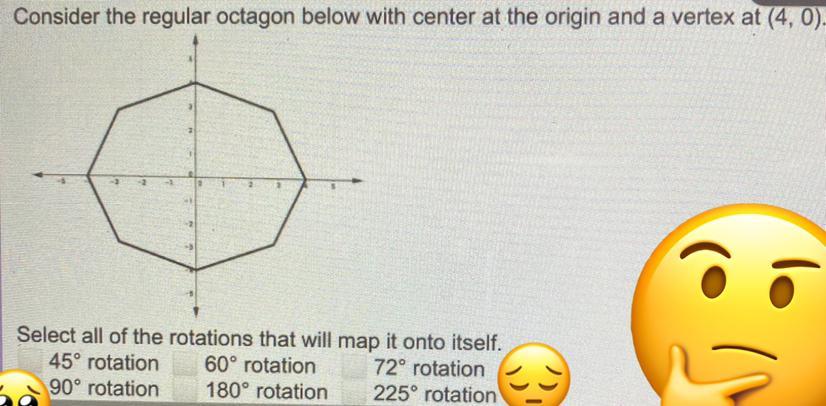
Answers
Answer:
90 degrees, and 180 degrees
Step-by-step explanation:
it flips, turns a little so 90 and 180 degrees
Assume that demand for a commodity is represented by the equation
P = -2Q-2Q_d
Supply is represented by the equation
P = -5+3Q_1
where Q_d and Q_s are quantity demanded and quantity supplied, respectively, and Pis price
Instructions: Round your answer for price to 2 decimal places and enter your answer for quantity as a whole number Using the equilibrium condition Q_s = Q_d solve the equations to determine equilibrium price and equilibrium quantity
Equilibrium price = $[
Equilibrium quantity = units
Answers
The equilibrium price is $0 and the equilibrium quantity is 5 units.
To find the equilibrium price and quantity, we need to set the quantity demanded equal to the quantity supplied and solve for the equilibrium values.
Setting Q_d = Q_s, we can equate the equations for demand and supply:
-2Q - 2Q_d = -5 + 3Q_s
Since we know that Q_d = Q_s, we can substitute Q_s for Q_d:
-2Q - 2Q_s = -5 + 3Q_s
Now, let's solve for Q_s:
-2Q - 2Q_s = -5 + 3Q_s
Combine like terms:
-2Q - 2Q_s = 3Q_s - 5
Add 2Q_s to both sides:
-2Q = 5Q_s - 5
Add 2Q to both sides:
5Q_s - 2Q = 5
Factor out Q_s:
Q_s(5 - 2) = 5
Q_s(3) = 5
Q_s = 5/3
Now that we have the value for Q_s, we can substitute it back into either the demand or supply equation to find the equilibrium price. Let's use the supply equation:
P = -5 + 3Q_s
P = -5 + 3(5/3)
P = -5 + 5
P = 0
Therefore, the equilibrium price is $0 and the equilibrium quantity is 5 units.
Learn more about supply equation here:brainly.com/question/13218367
#SPJ11
a roller coaster train with 6 passenger cars and the front decoration has a mass of 3,500kg. when the train has the front decoration and only 4 passenger cars, it has a mass of 2,400kg.
what is the mass of the decoration and of each passenger car?
Answers
The mass of the decoration and of each passenger car are 200 kg and 550 kg, respectively
How to determine the masses?The given parameters in the question are
6 passenger cars and the front decoration = 3,500kg4 passenger cars and the front decoration = 2,400kgThese can be represented as
(6, 3500) and (4, 2400)
The slope of the above points represent the mass of each passenger car
This is calculated as
Slope = Difference in mass/Difference in number of cars
So, we have
Slope = (3500 - 2400)/(6 - 4)
Evaluate
Slope = 550
When there are no passenger cars in the train, we have
(0, Mass of decoration)
Using the slope formula, we have
Slope = (Mass of decoration - 3500)/(0 - 6)
So, we have
Slope = (Mass of decoration - 3500)/(-6)
This gives
(Mass of decoration - 3500)/(-6) = 550
Cross multiply
Mass of decoration - 3500 = -3300
Add 3500 to both sides
Mass of decoration = 200
Hence, the mass of each car is 550 kg
Read more about slope at
https://brainly.com/question/29135291
#SPJ1
Select the correct description for the expression x+3/5
A. The quotient of a sum and a number
B. The quotient of a difference and a number
C. The product of a number and a sum
D. The product of a number and a difference
Answers
Answer:
the answer is A that's the answer
Algebra solve the equation show work

Answers
Start by subtracting 3t from one side to get the variables both on one side
0t + 4 = 12
No solution as 0 can’t be a coefficient
Answer:
Step-by-step explanation:
3t + 4 = 12 + 3t
4 = 12 (subtract 3t from both sides)
0 = 8 (subtract 4 from both sides)
I already figured out one i think need help ASAP!!!!
Answers
Answer:
Need help with what?
Step-by-step explanation:
Find the indefinite integral by making a change of variables. (Use C for the constant of integration.) ∫(x + 5)√(2 – x) dx
Answers
The indefinite integral of\(\int\limits^a_b {(x+5)}\sqrt{2-2} \, dx\) is \((2/5)(2-x)^{5/2} - (14/3)(2-x)^{3/2} +C\)
To find the indefinite integral of ∫(x + 5)√(2 – x) dx by making a change of variables, follow these steps:
1. Choose a substitution for one of the variables. Let's substitute u for (2-x):
u = 2 - x
2. Differentiate both sides of the equation with respect to x to find du/dx:
du/dx = -1
3. Rearrange the equation to isolate dx:
dx = -du
4. Substitute the expressions for u and dx back into the integral:
∫(x + 5)√(2 – x) dx = ∫(2 - u + 5)√u (-du)
Simplify the expression:
∫(7 - u)√u (-du)
5. Now, evaluate the integral:
-∫(7 - u)√u du
6. Distribute the -1 into the integrand and split the integral into two separate integrals:
∫(u√u - 7√u) du
7. Rewrite the integrals using exponents instead of radicals:
∫(u^(3/2) - 7u^(1/2)) du
8. Integrate each term separately:
(2/5)u^(5/2) - (14/3)u^(3/2) + C
9. Substitute back the original variable, x, for u:
(2/5)(2-x)^(5/2) - (14/3)(2-x)^(3/2) + C
Therefore, the indefinite integral of ∫(x + 5)√(2 – x) dx is (2/5)(2-x)^(5/2) - (14/3)(2-x)^(3/2) + C.
To know more about "INDEFINITE INTEGRALS" refer here:
https://brainly.com/question/12231722#
#SPJ11
The shape of the distribution of the time required to get an oil change at a 20 minute oil change facility is unknown, however the records indicate that the mean time is 21.6 minutes and the standard deviation is 4.4 minutes.
What is the probability that a random sample of n=40 oil changes will result in a sample mean time less than 20 minutes?
Answers
The probability that a random sample of n = 40 oil changes will result in a sample mean time of less than 20 minutes is approximately 0.0495, or 4.95%.
To find the probability that a random sample of n = 40 oil changes will result in a sample mean time of fewer than 20 minutes, we can use the Central Limit Theorem. The Central Limit Theorem states that for a large enough sample size, the distribution of sample means will be approximately normal, regardless of the shape of the original population distribution.
In this case, we know the meantime of the oil change population is μ = 21.6 minutes and the standard deviation is σ = 4.4 minutes. Since the sample size (n = 40) is reasonably large, we can assume that the distribution of the sample mean time will be approximately normal.
To calculate the probability, we need to standardize the sample mean using the z-score formula:
z = (x - μ) / (σ / √n)
where x is the desired value (20 minutes), μ is the population mean (21.6 minutes), σ is the population standard deviation (4.4 minutes), and n is the sample size (40).
z = (20 - 21.6) / (4.4 / √40) ≈ -1.654
Now, we need to find the probability of a z-score less than -1.654 using a standard normal distribution table or a statistical calculator. Looking up this value, we find that the probability is approximately 0.0495.
Therefore, the probability that a random sample of n = 40 oil changes will result in a sample mean time of fewer than 20 minutes is approximately 0.0495, or 4.95%.
To know more about probability follow
https://brainly.com/question/14085551
#SPJ4
in october 2012, apple introduced a much smaller version of the apple ipad, known as the ipad mini. weighing less than 11 ounces, it was 50% lighter than the standard ipad. battery tests for the mini ipad showed that battery life is uniformly distributed between 8.5 and 12 hours. what is the value of 'a'? answer to one decimal.
Answers
a) The Probability density function of given uniform distribution example is
F(x) = 1/3.5 for 8.5 < x< 12
Uniform distribution in Statistics is a type of probability distribution in which all possible outcomes have equally likely chance to occur. It is generally represented by U(x,y) where
x ---> minimum value and y---> maximum value
Probability density function is a probability function which defines the density of continuous random variable lying between specified range
values. It is denoted by f( a<X<b)
Probability density function for uniform distribution is F(x) = 1/(b-a) for a<x<b where a and b are parameters of uniform distribution.
We have following informations,
weigh of mini iPad = 11 ounces or 50% lighter than standard iPad.
Assume that the battery of iPad is uniformly distributed between 8.5 hours to 12 hours.
this implies a = 8.5 , b = 12
F(x) = 1/(12 - 8.5) = 1/3.5 for 8.5<x<12
To learn more about Uniform distribution, refer :
https://brainly.com/question/28984186
#SPJ4
#Complete Qestion :
In October 2012, Apple introduced a much smaller variant of the Apple iPad, known as the iPad Mini. Weighing less than 11 ounces, it was about 50% lighter than the standard iPad. Battery tests for the mini ipad showed that battery life is uniformly distributed between 8.5 and 12 hours. what is the value of 'a'? answer to one decimal. Assume that the battery life of the iPad Mini is uniformly distributed between 8.5 and 12 hours.
a) What is the probability that the battery life for an iPad Mini will be 10 hours or less?
describe the sample space in terms of the condition (functional or defective) of each nozzle after a year. let ""f"" denote a functional nozzle after a year and ""d"" denote a defective one.
Answers
The sample space, in terms of the condition (functional or defective) of each nozzle after a year, can be represented using the symbols "f" and "d" to denote a functional and defective nozzle, respectively.
The possible outcomes in the sample space can be described as a combination of these symbols. For example, if we have three nozzles, the sample space could include outcomes such as "fff" (all three nozzles are functional), "dfd" (the first and third nozzles are functional, while the second one is defective), "ffd" (the first two nozzles are functional, while the third one is defective), and so on.
Each outcome in the sample space corresponds to a particular arrangement or configuration of functional and defective nozzles after a year. The sample space encompasses all the possible combinations and provides a comprehensive representation of the different outcomes that can occur.
To learn more about sample space, click here: brainly.com/question/30464166
#SPJ11
A research company desires to know the mean consumption of meat per week among males over age 27. They believe that the meat consumption has a mean of 4.7
pounds, and want to construct a 98 % confidence interval with a maximum error of 0.09 pounds. Assuming a variance of 1 pounds, what is the minimum number of
males over age 27 they must include in their sample? Round your answer up to the next integer.
Answers
Answer:
To construct a 98% confidence interval with a maximum error of 0.09 pounds and assuming a variance of 1 pound, the minimum sample size can be calculated using the formula:
n = (2 * standard error of the mean / margin of error)^2
Plugging in the values, we get:
n = (2 * (1 / sqrt(n)) / 0.09)^2
Solving for n, we get n = 832.6. Rounding up to the next integer, the minimum number of males over age 27 they must include in their sample is 833.
Step-by-step explanation:
AREA OF A CIRCLE PLS HELP

Answers
Answer:
153.86 ft²
Step-by-step explanation:
Area = \(\pi r^2\)
= 3.14 * 7 * 7
= 153.86 ft²
Answer:
if A =3.14*r^2 then the answer would be either 153.86
Step-by-step explanation:
5w + 9z = 2z + 3w solve for W
Answers
Answer:
w=-7/2z
Step-by-step explanation:
just ask
Step-by-step explanation:
\(5w + 9z = 2z + 3w\)
\(5w - 3w = 2z - (9z)\)
\(2w = - 7z\)
\(w = - 7z \div 2\)
\(w = - 7z \times \frac{1}{2} \\ \)
\(w = - \frac{7}{2} z \\ \)
◄x
Find the product 3 2/5 x 5/3
Answers
Explanation. 3 2/5 = 17/5
So 17/5 x 5/3 the 5’s will cancel out to leave 17/3 = 5 2/3
I hope this helps!!
in order to determine an interval for the mean of a population with unknown standard deviation, a sample of 59 items is selected. the mean of the sample is determined to be 32. what is the associated number of degrees of freedom for reading the t value?
Answers
The associated number of degrees of freedom for reading the t-value is 58.
The aim is to determine an interval for the mean of a population.
The standard deviation is unknown to us. The sample consists of 59 items. The mean of the sample is determined to be 32. We need to calculate the associated number of degrees of freedom for reading the t value.
We know that the degree of freedom is one less than the number of items in the sample space.
The associated number of degrees of freedom for reading the t-value is 59-1.
The associated number of degrees of freedom for reading the t-value is 58.
To learn more about standard deviation, visit :
brainly.com/question/13905583
#SPJ4
