please help me use comparison theorem to solve: [infinity]∫1 4x √ x+2e^-x/4
Answers
Since the integral of g(x) from 1 to ∞ diverges, and \(4x√(x+2e^(-x/4))\)is less than or equal to g(x) for x ≥ 1, we can conclude that the given integral \(∫[1, ∞] 4x√(x+2e^(-x/4)) dx\) also diverges.
To use the comparison theorem to solve the integral \(∫[1, ∞] 4x√(x+2e^(-x/4)) dx\), we need to find a function g(x) that is larger than or equal to \(4x√(x+2e^(-x/4))\pi 4x√(x+2e^(-x/4))\) for all x ≥ 1. Then we can compare the integral of g(x) with the given integral to determine its convergence or divergence.
Let's consider g(x) = 4x√x. We can show that g(x) is greater than or equal to \(4x√(x+2e^(-x/4))\) for x ≥ 1.
For x ≥ 1, we have:
\(√(x+2e^(-x/4)) ≤ √(x+x) = √(2x)\\So, 4x√(x+2e^(-x/4)) ≤ 4x√(2x) = 4√(2)x^(3/2)\)
Now, let's integrate g(x) = 4x√x from 1 to ∞:
∫[1, ∞] 4x√x dx = lim[a→∞] ∫[1, a] 4x√x dx
= lim[a→∞] [8/3 * x\(^(3/2)\)] from 1 to a
= lim[a→∞] [8/3 * a\(^(3/2)\) - 8/3 * 1\(^(3/2)\)]
= lim[a→∞] [8/3 * a\(^(3/2)\) - 8/3]
= ∞
Since the integral of g(x) from 1 to ∞ diverges, and 4x√(x+2e\(^(-x/4)\)) is less than or equal to g(x) for x ≥ 1, we can conclude that the given integral ∫[1, ∞] 4x√(x+2e^(-x/4)) dx also diverges.
To know more about integral, visit:
https://brainly.com/question/29892964
#SPJ11
Related Questions
The area of a rectangle is 8811m if the width of the garden is 89 m what’s the length
Answers
The length of the garden is 99 m.
What’s the length?The formula for the area of a rectangle is:
Area = Length x Width
We are given that the area of the rectangle is 8811 \(m^{2}\) and the width is 89 m. Substituting these values into the formula, we get:
8811 \(m^{2}\) = Length x 89 m
To solve for the length, we can divide both sides of the equation by 89 m:
Length = 8811 \(m^{2}\) / 89 m
Simplifying, we get:
Length = 99 m
Therefore, the length of the garden is 99 m.
to know more about rectangle
brainly.com/question/29123947
#SPJ1
xplain why a 2 2 matrix can have at most two distinct eigenvalues. explain why an n n matrix can have at most n distinct eigenvalues.
Answers
The total number of eigenvectors for an n x n matrix is equal to the sum of the multiplicities of its distinct eigenvalues,
which is at most n.
The reason why a 2x2 matrix can have at most two distinct eigenvalues is because the characteristic equation for a
2x2 matrix is quadratic. This means that there can be at most two distinct solutions for the eigenvalues.
As for an n x n matrix, the reason why it can have at most n distinct eigenvalues is because the characteristic equation
for an n x n matrix is of degree n.
This means that there can be at most n distinct solutions for the eigenvalues. Additionally, the maximum number of
eigenvectors that can be associated with each distinct eigenvalue is equal to the multiplicity of the eigenvalue.
Therefore, the total number of eigenvectors for an n x n matrix is equal to the sum of the multiplicities of its distinct
eigenvalues, which is at most n.
for such more question on total number
https://brainly.com/question/9879870
#SPJ11
Find the probability for the spinner
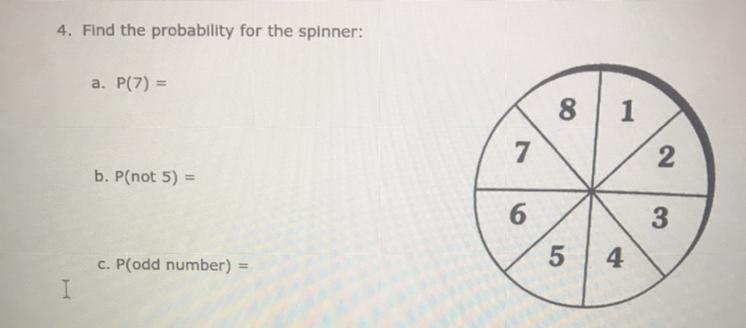
Answers
Determine the values of k so that the following linear system of equations (in x, y and z) has:
(i) a unique solution; (ii) no solution; (iii) an infinite number of solutions.
2x + (k + 1)y + 2z = 3
2x + 3y + kz = 3
3x + 3y − 3z = 3
Answers
The values are (i) Unique solution: k ≠ 2
(ii) No solution: k = 2
(iii) Infinite solutions: k = 2
To determine the values of k for the given linear system, we can analyze the coefficient matrix and the augmented matrix.
The coefficient matrix is:
[ 2 (k + 1) 2 ]
[ 2 3 k ]
[ 3 3 -3 ]
We can perform row operations to simplify the matrix:
R2 = R2 - R1
R3 = R3 - R1
The simplified matrix becomes:
[ 2 (k + 1) 2 ]
[ 0 (2 - k) (k - 2) ]
[ 0 (2 - k) (-5) ]
Now, let's analyze the augmented matrix:
[ 2 (k + 1) 2 | 3 ]
[ 0 (2 - k) (k - 2) | 0 ]
[ 0 (2 - k) (-5) | 0 ]
(i) For a unique solution, the coefficient matrix must be non-singular, which means its determinant must be nonzero. Thus, we need to find the values of k for which the determinant of the coefficient matrix is nonzero.
(ii) For no solution, the coefficient matrix and the augmented matrix must have different ranks. So, we need to determine the values of k for which the rank of the coefficient matrix differs from the rank of the augmented matrix.
(iii) For an infinite number of solutions, the coefficient matrix and the augmented matrix must have the same rank, and the rank must be less than the number of variables. Thus, we need to find the values of k for which the rank of both matrices is equal and less than 3.
By analyzing the determinant and ranks, we can determine the values of k for each case.
To know more about linear system of equations refer here:
https://brainly.com/question/20379472
#SPJ11
Drag the expressions to the correct functions. Not all expressions will be used.
Consider the functions fand g.
= 4x² + 1
g(x) =
Perform the function compositions:
x² - 3
Answers
The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)).
Let the functions be f(x) = 4x² + 1 and g(x) = x² - 3
The correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
What is composition function?The function composition exists an operation " ∘ " that brings two functions f and g, and has a function h = g ∘ f such that h(x) = g(f(x)). In this operation, the function g exists used for the outcome of applying the function f to x.
Given:
f(x) = 4x² + 1 and g(x) = x² - 3
a) (f o g)(x) = f[g(x)]
f[g(x)] = 4(x² - 3)² + 1
substitute the value of g(x) in the above equation, and we get
= 4(x⁴ - 24x + 9) + 1
simplifying the above equation
= 4x⁴ - 96x + 36 + 1
= 4x⁴ - 96x + 37
(f o g)(x) = 4x⁴ - 96x + 37
b) (g o f)(x) = g[f(x)]
substitute the value of g(x) in the above equation, and we get
g[f(x)] = (4x² + 1)²- 3
= 16x⁴ + 8x² + 1 - 3
simplifying the above equation
= 16x⁴ + 8x² - 2
(g o f)(x) = 16x⁴ + 8x² - 2.
Therefore, the correct answer is (f o g)(x) = 4x⁴ - 96x + 37 and
(g o f)(x) = 16x⁴ + 8x² - 2.
To learn more about the function refer to:
https://brainly.com/question/26709985
#SPJ9
Help Help Help .!
repeated multiplication using a negative fraction .

Answers
\( {4}^{3} = 63\)
Solving system of Equations:
x-4y= -14
x+5y= 13
What is y?
Answers
Answer:
x=-2, y=3. (-2, 3).
Step-by-step explanation:
x-4y=-14
x+5y=13
--------------
-x+4y=14
x+5y=13
----------------
9y=27
y=27/9
y=3
x+5(3)=13
x+15=13
x=13-15
x=-2
DOES THIS SET OF ORDERED PAIRS
REPRESENT A FUNCTION?
{(2,4),(2,5), (2,6), (2,7) }
Answers
No, this set of ordered pairs does not represent a function.
Explanation:
Functions have one y-value for a given x-value.
Ordered pairs are written (x, y).
In this set, when x=2, it has four y-values (4, 5, 6 and 7), so it cannot be a function.
Answer:
No
Step-by-step explanation:
No, this set of ordered pairs does not represent a function because functions a relation in which each input has only one output.
3.12 If h(t)= [u(t-1)- u(t - 4)] and x(t) = t[u(t)- u(t-2)], obtain graphically the response y(t). For what value of t does y(t) reach its maximum value?
Answers
The response y(t) graphically, we can first plot the individual functions h(t) and x(t) on a graph, and then determine their convolution to obtain y(t). Let's go step by step:
Plotting h(t):
The function h(t) is defined as h(t) = [u(t-1) - u(t-4)].
The unit step function u(t-a) is 0 for t < a and 1 for t ≥ a. Based on this, we can plot h(t) as follows:
For t < 1, h(t) = [0 - 0] = 0
For 1 ≤ t < 4, h(t) = [1 - 0] = 1
For t ≥ 4, h(t) = [1 - 1] = 0
So, h(t) is 0 for t < 1 and t ≥ 4, and it jumps up to 1 between t = 1 and t = 4. Plotting h(t) on a graph will show a step function with a jump from 0 to 1 at t = 1.
Plotting x(t):
The function x(t) is defined as x(t) = t[u(t) - u(t-2)].
For t < 0, both u(t) and u(t-2) are 0, so x(t) = t(0 - 0) = 0.
For 0 ≤ t < 2, u(t) = 1 and u(t-2) = 0, so x(t) = t(1 - 0) = t.
For t ≥ 2, both u(t) and u(t-2) are 1, so x(t) = t(1 - 1) = 0.
So, x(t) is 0 for t < 0 and t ≥ 2, and it increases linearly from 0 to t for 0 ≤ t < 2. Plotting x(t) on a graph will show a line segment starting from the origin and increasing linearly with a slope of 1 until t = 2, after which it remains at 0.
Obtaining y(t):
To obtain y(t), we need to convolve h(t) and x(t). Convolution is an operation that involves integrating the product of two functions over their overlapping ranges.
In this case, the convolution integral can be simplified because h(t) is only non-zero between t = 1 and t = 4, and x(t) is only non-zero between t = 0 and t = 2.
The convolution y(t) = h(t) * x(t) can be written as:
y(t) = ∫[1,4] h(τ) x(t - τ) dτ
For t < 1 or t > 4, y(t) will be 0 because there is no overlap between h(t) and x(t).
For 1 ≤ t < 2, the convolution integral simplifies to:
y(t) = ∫[1,t+1] 1(0) dτ = 0
For 2 ≤ t < 4, the convolution integral simplifies to:
y(t) = ∫[t-2,2] 1(t - τ) dτ = ∫[t-2,2] (t - τ) dτ
Evaluating this integral, we get:
\(y(t) = 2t - t^2 - (t - 2)^2 / 2,\) for 2 ≤ t < 4
For t ≥ 4, y(t) will be 0 again.
Maximum value of y(t):
To find the value of t at which y(t) reaches its maximum value, we need to examine the expression for y(t) within the valid range 2 ≤ t < 4. We can graphically determine the maximum by plotting y(t) within this range and identifying the peak.
Plotting y(t) within the range 2 ≤ t < 4 will give you a curve that reaches a maximum at a certain value of t. By visually inspecting the graph, you can determine the specific value of t at which y(t) reaches its maximum.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
help please i really need help

Answers
Answer:
I think the next one 400
H(-9,3) and A (8,-3)Find the midpoints?
Answers
The given points are
\(\begin{gathered} H(-9,3) \\ A(8,-3) \end{gathered}\)We are asked to find the midpoint.
Recall that the midpoint formula is given by
\((x,y)=\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\)We have
\(\begin{gathered} x_1=-9 \\ x_2=8 \\ y_1=3 \\ y_2=-3 \end{gathered}\)Substitute the given values into the midpoint formula.
\(\begin{gathered} (x,y)=\frac{-9+8}{2},\frac{3-3}{2} \\ (x,y)=\frac{-1}{2},\frac{0}{2} \\ (x,y)=(-\frac{1}{2},0) \end{gathered}\)Therefore, the midpoint of H(-9, 3) and A (8, -3) is found to be
\((x,y)=(-\frac{1}{2},0)\)Or it can also be written in the decimal notation as
\((x,y)=(-0.5,0)\)
There are 3 roads to the top of the mountain. How many ways to
climb and come down from the mountain exist if the tourist should
take different ways?
Answers
:There are 9 ways for the tourist to climb up and come down the mountain if different routes are taken.
To find the number of ways to climb and come down from the mountain that exist if the tourist should take different ways given that there are 3 roads to the top of the mountain, we use the multiplication principle of counting.
If the tourist should take different ways, then the choices for going up and coming down can be different. There are 3 ways to go up the mountain, and for each of the 3 ways to go up, there are also 3 ways to come down. Therefore, the number of ways to climb up and come down from the mountain is the product of the number of ways to go up and come down i.e. 3 × 3 = 9 ways.
:There are 9 ways for the tourist to climb up and come down the mountain if different routes are taken.
To know more about multiplication principle visit:
brainly.com/question/17514196
#SPJ11
2] The band has a ratio of boys to girls of 5 to 4. There are 52 girls in the band.
(Make sure to write out in words first.)
How many are boys?
How many total students?
I need work for both
Answers
Answer:
Step-by-step explanation:
For every 4 boys there are 5 girls and 9 students at the school. So that means that 49 of the students are boys. 49 of the total number of students is 120 students:
49×?=120
If 49 the number of students is 120, then 14 of 120 is 19 of the total number of students. In other words, 14×120=30 is 19 the total number of students. Then 9 times this amount will give the total number of students:
9×30=270
So there is a total of 270 students at the school. Note that this is equivalent to finding the answer to the division problem:
120÷49=?
We can see all of this very succinctly by using a tape diagram:
Bar_diagram_67722d3e6005449e4fbe5c57eaad4f3c
There are 4 units of boys and 9 units of students. Therefore 4/9 of the students are boys.
4 units = 120
1 unit = 30
9 units = 270
There are 270 students altogether.
Students can multiply the numbers in the first row by 10 to get the second row, and then double that amount to get the third row. Adding the entries in the second and third row gives the fourth row that has the solution.
Alternatively, since 120÷4=30, students can just multiply the numbers in the first row by 30 to get the values in the fourth row.
In every row, we can see that the fraction of the students that are boys is 49.
looking at the last row, we can see that the total number of students will be 4×30+5×30=120+150=270.
A triangle has sides of length 2 cm, 8 cm and 9 cm.
Calculate the value of the largest angle in this triangle.
:)
Answers
Answer:
113.97 degrees
Step-by-step explanation:
use the cosine rule for finding an angle
cosA = b^2 + c^2 - a^2
2bc
In the given triangle angle A is greatest than any other angle.
What is the triangle?A triangle is a polygon with three vertices and three sides. The angles of the triangle are formed by the connection of the three sides end to end at a point. The triangle's three angles add up to 180 degrees in total.
Given sides of triangle, a=2cm,b=8cm,c=9cm
cosine law
Cos A = \(\frac{-a^2 + b^2 + c^2}{ 2bc}\) = \(\frac{64 + 81 - 4 }{2 * 8 *9}\) = 141/ 144
Cos B = \(\frac{a^2 - b^2 + c^2}{ 2ac}\) = \(\frac{4 + 81 - 64}{2 * 2 *9}\) = 21/36
Cos C = \(\frac{a^2 + b^2 - c^2}{ 2ab}\) = \(\frac{4 + 64 -81}{2 * 2* 8}\) = -13/52
A = Cos⁻¹ (141 /144 )
B = Cos⁻¹ (21/ 36 )
C = Cos⁻¹ (-13/52 )
Thus Angle A < Angle B < Angle C.
Therefore, Angle A is the greatest in the triangle.
Learn more about triangles here:
https://brainly.com/question/14712269
#SPJ2
I drove 10 miles north 14 miles east 16 miles north 2 miles east 4 miles north how far am I
Answers
The total distance from the starting point is 42 miles.
What is distance?Distance is a numerical measurement of how far apart two objects or points are located. It can be measured in various units, such as miles, kilometers, or light years. The concept of distance is important in physics, mathematics, and geometry. It is used in a wide range of everyday applications, from measuring the length of a running track to determining the distance from Earth to the Moon. Distance helps us understand how things are related and connected to each other in space. It can also be used to calculate the speed of an object or the time it takes to travel between two points.
To calculate this, one can use the Pythagorean theorem to solve for the hypotenuse of the right triangle created by the distances traveled. The hypotenuse of the triangle is the total distance traveled, and can be calculated by taking the square root of the sum of the squares of the other two sides. The other two sides are the 10 miles north and the 16 miles east, so the total distance traveled can be calculated by taking the square root of (10^2 + 16^2). The answer is 42 miles.
To know more about distance click-
https://brainly.com/question/23848540
#SPJ1
Complete questions as follows-
I drove 10 miles north 14 miles east 16 miles north 2 miles east 4 miles north how far am I from my starting point?
Pls help due tomorrow!!!!!!!!!!:

Answers
The answer is 15ab
Step-by-step explanation:
Since (x + y)² = (x + y)(x + y) = x² + 2xy + y²
(3a + 2.5b)²
9a² + 2(3a)(2.5b) + 6.25b²
9a² + 15ab + 6.25b²
Hence, (3a + 2.5b)² = 9a² + 6.25b² + 15ab
find the solution to the following system using subsitution or elimination y=2x-1 y=5x-7

Answers
If z = 2x2 - 3y with u = x2 siny and v= 2y cosx, determine expressions for dz/du and dz/dv
Answers
The expressions for dz/du and dz/dv are as follows:
dz/du = 4x siny
dz/dv = -6y cosx
To find the expressions for dz/du and dz/dv, we need to differentiate the given function z = 2x^2 - 3y with respect to u and v, respectively.
1. dz/du:
Since u = x^2 siny, we can express z in terms of u by substituting x^2 siny for u in the original function:
z = 2u - 3y
Now, we differentiate z with respect to u while treating y as a constant:
dz/du = d/dx (2u - 3y)
= 2(d/dx (x^2 siny)) - 0 (since y is constant)
= 2(2x siny)
= 4x siny
Therefore, dz/du = 4x siny.
2. dz/dv:
Similarly, we express z in terms of v by substituting 2y cosx for v in the original function:
z = 2x^2 - 3v
Now, we differentiate z with respect to v while treating x as a constant:
dz/dv = d/dy (2x^2 - 3v)
= 0 (since x^2 is constant) - 3(d/dy (2y cosx))
= -6y cosx
Therefore, dz/dv = -6y cosx.
In summary, the expressions for dz/du and dz/dv are dz/du = 4x siny and dz/dv = -6y cosx, respectively.
To learn more about expressions, click here: brainly.com/question/4344214
#SPJ11
psllslsslslslsl help ASAP BRAINLIST

Answers
Answer:
24.94
Step-by-step explanation:
To find shipping and handling take the price and multiply by the shipping and handling percent
464 * 5.375%
Change to decimal form
464 * .05375
24.94 for shipping and handling
What is the probability that either event will occur?
Now, find the probability of event A and event B.
A
B
6
6
20
20
P(A and B) = [?]

Answers
The probability P(A and B) that both events will occur is 8/13
Calculating the probability that both events will occur?From the question, we have the following parameters that can be used in our computation:
Event A = 6 and 6
Event B = 20 and 6
Event A and B = 6
Total = 6 + 6 + 20 + 6 - 6 + 20 = 52
Using the above as a guide, we have the following:
P(A) = 12/52
P(B) = 26/52
P(A and B) = 6/52
The probability that both events will occur is represented as
P(A and B) = P(A) + P(B) - P(A and B)
And this is calculated as
P(A and B) = P(A) + P(B) - P(A and B)
Substitute the known values in the above equation, so, we have the following representation
P(A and B) = 12/52 + 26/52 - 6/52
Evaluate
P(A and B) = 32/52
Simplify
P(A and B) = 8/13
Hence, the probability that both events will occur is 8/13
Read more about probability at
brainly.com/question/31649379
#SPJ1
The volume of a gas halved during an adiabatic compression that increases the pressure by a factor of 2.5 What is the specific heat ratio?
Answers
A ratio in mathematics displays how often one number occurs in another and the given situation's specific heat ratio is 1.24.
What is the ratio?In mathematics, a ratio shows how frequently one number appears in another.
For instance, the ratio of oranges to lemons in a fruit plate would be eight to six if there were eight oranges and six lemons.
Oranges make up 8:14 of the total fruit, whereas lemons make up 6:8 of the total fruit.
So, e are informed that the volume is halved, and the pressure increases by a factor of 2.5.
We shall therefore have:
PVγ = 2.5P(0.5V)γ
We'll condense this to:
(1/0.5)γ = 2.5
γ = In2.5/In2
γ = 1.32
The volume temperature relation is written as follows if the volume expands in an adiabatic process:
T1V1∧γ-1 = T2V2∧γ-1
T1V1∧1.32-1 = T2(0.5V1)∧1.32-1
Condensing this results in:
T₁ = 1.24T₂
Therefore, a ratio in mathematics displays how often one number occurs in another and the given situation's specific heat ratio is 1.24.
Know more about the ratios here:
https://brainly.com/question/2328454
#SPJ4
Light sample A has a frequency of 4.30×1015 Hz and light sample B has a frequency of 8.70×1018 Hz. What is the wavelength of light sample A in meters? Light sample A has a frequency of 4.30×1015 Hz and light sample B has a frequency of 8.70×1018 Hz. What is the wavelength of light sample B in meters? Light sample A has a frequency of 4.30 ×1015 Hz and light sample B has a frequency of 8.70×1018 Hz. Based on frequency, which set gives the most correct description of the types of light for samples A and B respectively? Light sample A has a frequency of 4.30 ×1015 Hz and light sample B has a frequency of 8.70×1018 Hz. Based on frequency, which set gives the most correct description of the types of light for samples A and B respectively?
Answers
1) The wavelength of A is equal to 6.98 × \(10^{-8}\)meters
2) The wavelength of B is equal to 3.45 × \(10^{-11}\) meters
Since we know that the wavelength = speed of light / frequency
The speed of light is 3.00 × \(10^8\) meters per second.
For light sample A with a frequency of 4.30 × 10^15 Hz can be calculated as;
wavelength of A = (3.00 × \(10^8\) m/s) / (4.30 × 10^15 Hz)
wavelength of A = 6.98 × \(10^{-8}\) meters
For light sample B with a frequency of 8.70 × \(10^18\) Hz can be calculated as;
wavelength of B = (3.00 × \(10^8\) m/s) / (8.70 ×\(10^18\) Hz)
wavelength of B = 3.45 × \(10^{-11}\) meters
Learn more about wavelength:
brainly.com/question/31143857
#SPJ4
Max has a square piece of cloth. He cuts it in half from one corner to the opposite corner. How many sides does each of the cut pieces have?
Answers
Answer:
Step-by-step explanation:
You have a cloth:
____________
| |
| |
|___________|
and you cut it in half.
There are three sides
Answer:
Step-by-step explanation:
The cut pieces will each have three sides: two that are equal and one that is the hypotenuse.
If the original square had sides of length s, then the cut pieces would each have two of that length: s and s; the third side would have length h = √(s² + s²), or h = s√2.
find the area of this circle

Answers
Answer:
A= πr²
where pi = 3
and r = 3
A = 3 x 3²
3 x 9
area = 27 ft²
You are planning to join a gym. Muscles Gym costs $100 to join and $25 each month (
) and Cardio Gym costs nothing to join and $50 each month (
).
Solve this linear system and choose the true statement below. (Look carefully at the order of the numbers in the solution.)
The solution is (200, 4). This means that it will cost me $200 to go to either gym 4 times.
The solution is (4, 200). This means that it will cost me $200 to go to either gym 4 times.
The solution is (200, 4). This means that at 4 months of membership, either gym will cost $200.
The solution is (4, 200). This means that at 4 months of membership, either gym will cost $200.
Answers
Answer:
The answer is: (B)
The solution is (4, 200). This means that it will cost me $200 to go to either gym 4 times.
the equations given to you were:
(C = 100 + 25x) and (C = 50x)
well, if you plug in 200 for C and 4 for x you get these equations,
200 = 100 + 25(4), and 200 = 50(x)
I solved both step-by-step below.
1. C = 100 + 25x plug in points
200 = 100 + 25(4) solve the parenthesis's
200 = 100 + 100 combine like terms
200 = 200 both sides are equal
2. C = 50x plug in points
200 = 50(4) solve the parenthesis's
200 = 200 both sides are equal
what is the smallest numerical value that a poisson random variable can be?
Answers
A Poisson random variable represents the number of occurrences of an event in a fixed interval of time or space. It is a discrete random variable, which means that it can only take on integer values, starting from zero. Therefore, the smallest numerical value that a Poisson random variable can be is zero.
This means that there is a possibility that the event will not occur at all during the given interval. For example, if we are counting the number of customers who visit a store in an hour, it is possible that no customers show up during that hour, resulting in a Poisson random variable of zero.
However, the probability of this occurring depends on the average rate of the event occurring, which is denoted by the parameter λ in the Poisson distribution. The larger the value of λ, the smaller the probability of a Poisson random variable being zero.
To know more about Poisson refer here
https://brainly.com/question/30388228#
#SPJ11
5(x-3)-4(x-3) is equivalent to
Answers
Answer:
\(5\left(x-3\right)-4\left(x-3\right)=x-3\)
Step-by-step explanation:
Given the expression
\(5\left(x-3\right)-4\left(x-3\right)\)
solving the expression
\(5\left(x-3\right)-4\left(x-3\right)=5x\:-\:15\:-\:4x\:+\:12\)
\(= x - 3\)
Thus, the equivalent expression is
\(5\left(x-3\right)-4\left(x-3\right)=x-3\)
please help im stuck

Answers
set both equations equal to each other and solve
The park plans to hire 20 percent more than the minimum number of ticket sellers needed in order to account for sickness, vacation, and lunch breaks. How many ticket sellers should the park hire? Explain.
Answers
he area of a rectangle is 44m , and the length of the rectangle is less than twice the width. Find the dimensions of the rectangle.
Answers
Answer:
4m x 11m
Step-by-step explanation:
4 is your width. 11 is your length.
4 x 4=16 > 11