please help mee
△ABC was transformed using two rigid transformations.
a. Compare all of the corresponding parts (angles and sides) of the image and preimage. Describe the results.
b. Explain why the results are true.
A triangle has six parts (three angles and three sides). Suppose you have two triangles that you want to prove are congruent, but you don't know the rigid transformations that map one triangle to the other.
A a. How do you think you can prove the two triangles are congruent without using rigid transformations?
b. Suppose one of your classmates thinks they can prove the triangles are congruent by proving only two pairs of corresponding parts congruent. How would you respond to this classmate?
Note: Be sure to number your responses for each question, like this: 1a, 1b, 2a, 2b.

Answers
The corresponding parts are:
<A = <A' = <A"<B = <B' = <B"<C = <C' = <C"AB = A'B' = A"B"AC = A'C' = A"C"BC = B'C' = B"C"How to compare the sidesThe statement is given as:
△ABC was transformed using two rigid transformations.
The rigid transformations imply that:
The images of the triangle after the transformation would be equal
So, the corresponding parts are:
<A = <A' = <A"<B = <B' = <B"<C = <C' = <C"AB = A'B' = A"B"AC = A'C' = A"C"BC = B'C' = B"C"Why the results are true?The results are true because rigid transformations do not change the side lengths and the angle measures of a shape
How to prove that two triangles are congruent without using rigid transformations?To do this, we simply make use any of the following congruent theorems:
SSS: Side Side SideSAS: Side Angle SideAAS: Angle Angle SideHow to respond to this classmate?The classmate's claim is that
Only two pairs of corresponding parts are enough to prove the congruent triangle
The above is true because of the following congruent theorems:
SSS: Side Side SideSAS: Side Angle SideRead more about congruent theorems at
https://brainly.com/question/2102943
#SPJ1
Related Questions
Jernel has to figure out the area of her square garage. she knows that one side of the garage is equal to the length of her rabbit pen. the dimensions of the rectangular rabbit pen are 14 by 10. what is the area of the garage?
Answers
Answer: 196
Step-by-step explanation:
Just answered this...
14x14=196
How do you find the volume of parallelepiped with adjacent edges?
Answers
the parallelepipeds' volume with neighboring edges is 16
The faces of a parallelepiped, a three-dimensional shape, are all parallelograms. It derives from the Greek phrase "an thing having parallel plane." In essence, it is a three-dimensional shape or a prism with a parallelogram base that is created by six parallelogram sides.
\(\vec{(PQ)}=\) (3+1, 0-2 ,1-5) = (4 , -2 , -4)
\(\vec{(PR)}=\) (3-5, 0-1 ,1+1) = (-2 , -1 , 2)
\(\vec{(PS)}=\) (3-0, 0-4 ,1-2) = (3 , 4 , -1)
The scalar triple product is given by the determinant of the matrix (3X3) that has in the rows the three components of the three vectors:
\(\left[\begin{array}{ccc}+4&-2&-4\\-2&-1&+2\\3&-4&-1\end{array}\right]\)'
and the determinant is shown as an illustration using the Laplace rule (first row):
\(4[(-1)(-1) - (2)(-4)] -(-2) [(-2)(-1) - (2)(3)] +(-4)[(-2)(-4)-(-1)(3)]=4(1+8)+2(2-6)-4(8+3)=36-8-44=-16\)
So the volume is: V=\(|-16|\)=16
Learn more about parallelepiped
brainly.com/question/29140066
#SPJ4
The time (in minutes) taken for a dose of a certain drug to be effective as a sedative on lab animals is normally distributed with mean =1 and variance 2=0.01. What is the proportion of animals for which the time taken is between 1 and 1.1 minutes?
Answers
Answer:
Step-by-step explanation:
Let x be the random variable representing the time (in minutes) taken for a dose of a certain drug to be effective as a sedative on lab animals. Since it is normally distributed and the population mean and population standard deviation are known, we would apply the formula,
z = (x - µ)/σ
Where
x = sample mean
µ = population mean
σ = standard deviation
From the information given,
µ = 1
σ = √variance = √0.01 = 0.1
the probability that the time taken for a randomly selected animal is between 1 and 1.1 minutes is expressed as
P(1 ≤ x ≤ 1.1)
For x = 1,
z = (1 - 1)/0.1 = 0
Looking at the normal distribution table, the probability corresponding to the z score is 0.5
For x = 1.1
z = (1.1 - 1)/0.1 = 1
Looking at the normal distribution table, the probability corresponding to the z score is 0.84
Therefore,
P(1 ≤ x ≤ 1.1) = 0.84 - 0.5 = 0.34
The the proportion of animals for which the time taken is between 1 and 1.1 minutes is 0.34
Help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!



Answers
B is true. This my answer

Assume that you plan to use a significance level of α = 0.05 to test the claim that p1 = p2. Use the given sample sizes and numbers of successes to find the P-value for the hypothesis test.
n1 = 50 x1 = 8 n2 = 50 x2 = 7
Answers
The P-value for the hypothesis test is approx. 0.7064.
To find the P-value for the hypothesis test, we need to perform a two-sample proportion test. The formula to calculate the test statistic for this test is given by:
\(\[ z = \frac{{(\hat{p}_1 - \hat{p}_2) - 0}}{{\sqrt{\hat{p}(1 - \hat{p})\left(\frac{1}{{n_1}} + \frac{1}{{n_2}}\right)}}} \]\)
where \(\hat{p}_1\) and \(\hat{p}_2\) are the sample proportions, \(\hat{p}\) is the combined sample proportion, \(n_1\) and \(n_2\) are the sample sizes, and 0 is the hypothesized difference in proportions.
In this case, we have \(n_1 = 50\), \(x_1 = 8\) (number of successes in sample 1), \(n_2 = 50\), and \(x_2 = 7\) (number of successes in sample 2).
First, we calculate the sample proportions:
\(\[ \hat{p}_1 = \frac{x_1}{n_1} = \frac{8}{50} = 0.16 \]\)
\(\[ \hat{p}_2 = \frac{x_2}{n_2} = \frac{7}{50} = 0.14 \]\)
Next, we calculate the combined sample proportion:
\(\[ \hat{p} = \frac{x_1 + x_2}{n_1 + n_2} = \frac{8 + 7}{50 + 50} = 0.15 \]\)
Then, we calculate the standard error:
\(\[ SE = \sqrt{\hat{p}(1 - \hat{p})\left(\frac{1}{{n_1}} + \frac{1}{{n_2}}\right)} = \sqrt{0.15(1 - 0.15)\left(\frac{1}{50} + \frac{1}{50}\right)} \approx 0.0529 \]\)
Finally, we calculate the test statistic:
\(\[ z = \frac{(\hat{p}_1 - \hat{p}_2) - 0}{SE} = \frac{(0.16 - 0.14) - 0}{0.0529} \approx 0.3772 \]\)
To find the P-value, we look up the test statistic in the standard normal distribution table. In this case, the P-value is the probability of observing a test statistic greater than 0.3772 or less than -0.3772.
Consulting the table, we find that the P-value is approximately 0.7064. Therefore, the P-value for the hypothesis test is approximately 0.7064.
To know more about P-value refer here:
https://brainly.com/question/30461126
#SPJ11
several forces are applied to the pipe assembly shown. knowing that each section of pipe has inner and outer diameters equal to 36 and 44 mm, respectively, determine the normal and shearing stresses at point h located at the top of the outer surface of the pipe.
Answers
To determine the normal and shearing stresses at point h located at the top of the outer surface of the pipe assembly, additional information about the forces applied to the assembly is required. Without this information, a specific calculation cannot be provided. However, I can explain the concept of normal and shearing stresses in a general context.
In engineering mechanics, normal stress refers to the force per unit area acting perpendicular to a surface. It is calculated by dividing the applied force by the cross-sectional area. Normal stress can be tensile (pulling apart) or compressive (pushing together) depending on the direction of the force.
Shearing stress, on the other hand, refers to the force per unit area acting parallel to a surface. It arises when two adjacent layers of a material slide or deform relative to each other. Shearing stress is calculated by dividing the applied shearing force by the cross-sectional area.
To determine the normal and shearing stresses at point h, the magnitude and direction of the applied forces, as well as the geometry of the assembly, need to be provided.
To learn more about shear stress click here:
brainly.com/question/20630976
#SPJ11
The normal stress at point h located at the top of the outer surface of the pipe can be determined using the formula σ = P/A, where P is the applied force and A is the cross-sectional area. The shearing stress can be calculated using the formula τ = V/Q, where V is the applied shear force and Q is the first moment of area.
To calculate the normal stress at point h, we need to consider the applied forces acting on the pipe assembly. If we have the axial force P applied at point h, the normal stress can be calculated using the formula σ = P/A, where A is the cross-sectional area of the pipe. Since the pipe has an inner diameter of 36 mm and an outer diameter of 44 mm, the cross-sectional area can be calculated as A = π/4 * (D_outer^2 - D_inner^2), where D_outer and D_inner are the outer and inner diameters, respectively.
To calculate the shearing stress at point h, we need to consider the applied shear force V. The shearing stress can be calculated using the formula τ = V/Q, where Q is the first moment of area. The first moment of area can be calculated as Q = π/4 * (D_outer^4 - D_inner^4), considering the same pipe dimensions as before.
By substituting the values of P, A, V, and Q into the respective formulas, you can determine the normal stress and shearing stress at point h, located at the top of the outer surface of the pipe assembly.
to learn more about diameter click here:
brainly.com/question/13015686
#SPJ11
Solve the system using substitution: {y=5x-21 y=-7x+15
Answers
Answer:
code lazar
Step-by-step explanation:
Find the moment about the x-axis of a wire of constant density that lies along the curve y = √6x from x=0 to x = 3. The moment is 8. (Type an exact answer, using radicals as needed.)
Answers
The moment about the x-axis of the wire of constant density that lies along the curve y = √6x from x=0 to x=3 is 27.
To determine the moment about the x-axis of a wire of constant density that lies along the curve y = √6x from x=0 to x=3, we can use the formula for the moment of a curve about the x-axis:
Mx = ∫(y²)dx
We have that the wire has constant density, the expression y^2 represents the elemental mass along the curve.
Substituting y = √6x into the formula, we have:
Mx = ∫(√6x)²dx
= ∫(6x)dx
= 6∫xdx
= 6(x²/2)
= 3x²
To determine the moment about the x-axis, we evaluate the integral from x=0 to x=3:
Mx = ∫(3x²)dx from 0 to 3
= [3(x³/3)] from 0 to 3
= (x³) from 0 to 3
= 3^3 - 0^3
= 27
Therefore, the moment about the x-axis of the wire is 27.
To know more about moment about the x-axis refer here:
https://brainly.com/question/32066911#'
#SPJ11
-2/5x-9<9/10
solve and explain/show steps
Answers
I think that’s the answer if I read your question correctly. I hoped this helped!!!
Gianna is taking a multiple choice test with a total of 100 points available. Each question is worth exactly 5 points. What would be Gianna's test score (out of 100) if she got 3 questions wrong? What would be her score if she got xx questions wrong?
Answers
Answer:
Her test score would be an 85 because 5x3=15 and then you would subtract 15 from 100 which would be 85
equation would be x=100-(5y)
Answer:
\(85\)
Step-by-step explanation:
Let \(x\) equal the number of questions.
Let's find how many total questions there are:
\(100=5x\)
Divide by the coefficient of \(x\), which in this case is \(5.\)
\(20=x\)
So we have a total of \(20\) questions, each are worth \(5\) points.
Now, Gianna got \(3\) questions wrong, and if we know there are \(20\) total questions...
\(20-3\)
Solve.
\(20-3=17\)
So we know Gianna got \(17\) questions correct.
Let's use an expression to figure out her score.
Again, let \(x\) equal the number of questions.
\(5x\)
Substitute.
\(5(17)\)
Multiply.
\(85\)
Please help me out!!! There’s 25 questions I can’t
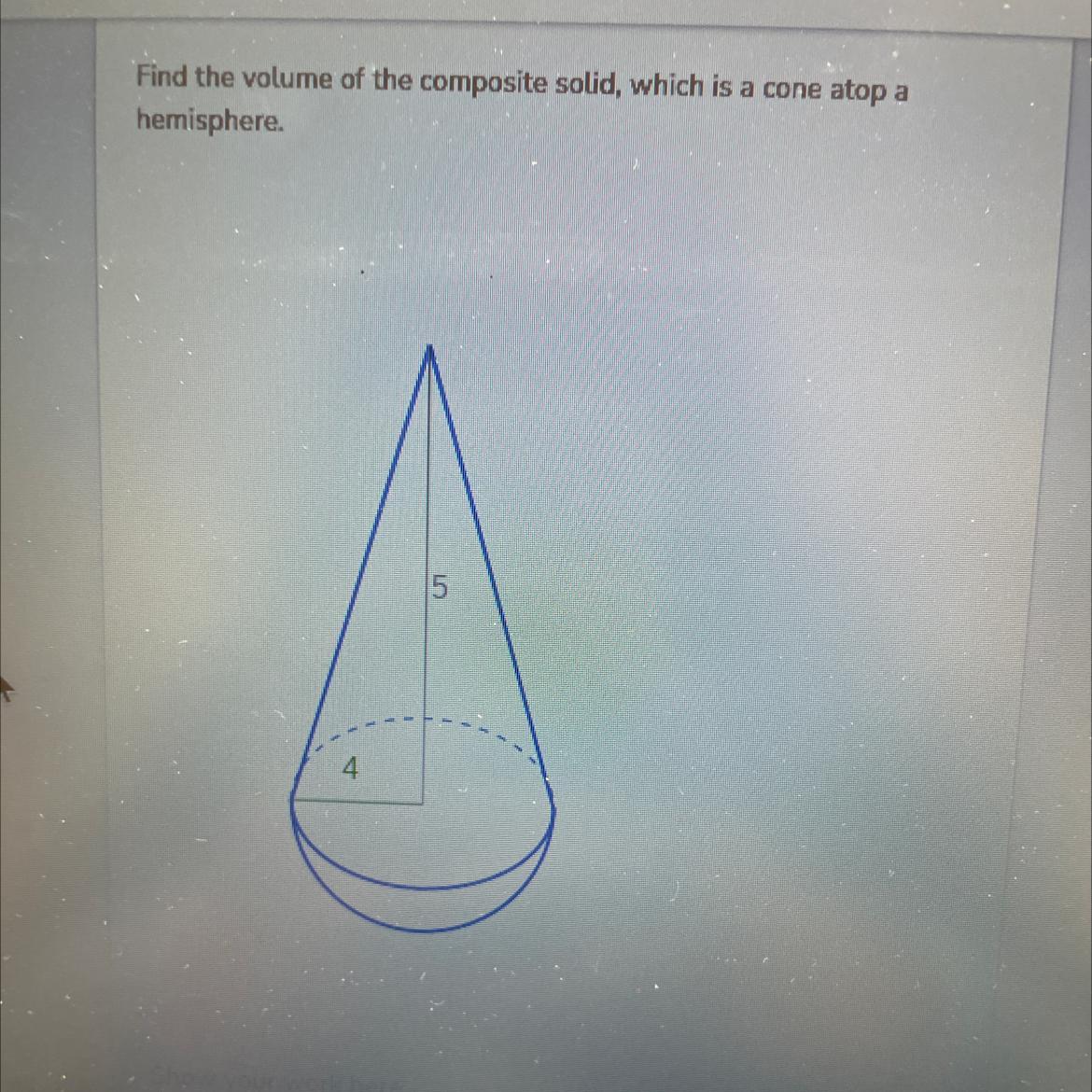
Answers
Answer:
217.70 cubic units
Step-by-step explanation:
Volume of composite solid Cone:h= 5 units & r = 4 units
\(\sf \boxed{Volume \ of \ cone = \dfrac{1}{3} \pi r^2h}\)
\(\sf = \dfrac{1}{3}*3.14*4*4*5\\\\ = 83.73 \ cubic units\)
Hemisphere:r = 4 units
\(\sf \boxed{Volume \ of \ hemisphere = \dfrac{2}{3} \pi r^3}\)
\(\sf = \dfrac{2}{3}*3.14*4*4*4\\\\= 133.97 \ cubicunits\)
Volume of composite solid = 83.73 + 133.97
= 217.70 cubic units
In this question we are provided with the height and radius. We are asked to calculate the volume of a composite solid
First we will find the volume of a cone
We know,
\( \orange{\star \: \small\boxed{ \sf{ Volume_{(cone)} = \dfrac{1}{3}πr²h}}}\)
Where,
r stand for radiush stand for heightAssuming π as 3.14Substituting the values we get
\( \small\bf Volume_{(cone)} = \dfrac{1}{3} \times 3.14×4 × 4×5\)
\( \rightarrow \small\rm{ Volume_{(cone)} = \dfrac{1}{3}×251.2}\)
\( \small\sf{ Volume_{(cone)} = 83.73 \:cubic \: units }\)
Now we will calculate the volume of a hemisphere
We know,
\( \red{\star \: \small \boxed{\sf{ Volume_{(hemisphere)} = \dfrac{2}{3}πr³}}}\)
Substituting the values we get
\( \small\bf{ Volume_{(hemisphere)} = \dfrac{2}{3} \times 3.14 × 4 × 4 × 4}\)
\( \rightarrow\small\rm{ Volume_{(hemisphere)} = \dfrac{2}{3} \times 200.96}\)
\( \rightarrow\small\rm{Volume_{(hemisphere)} = 2 \times 66.98} \)
\( \small\sf{ Volume_{(hemisphere)} =133.97}\)
Now we will calculate the volume
Volume = 83.73 + 133.97 = 217.70 cubic units
A number is randomly drawn from the set of numbers 1-20. The winning number is either 4 or odd.
Joey knows the answer is 12/20. What does the 12 represent? What does the 20 represent?
Answers
solve the system by substitution 6x-2y=26 and -y+3=x
Answers
Hope this helped! :)
Tamora's net pay is $420 per week. Create an equation for Tamora's net pay.
Answers
Answer: y = 420x
Step-by-step explanation:
y = Total pay
x = Number of weeks
420 = Number of dollars per week of net pay
pls help this is past due and I have no idea on how to do it

Answers
Answer:
42.3
Step-by-step explanation:
Substitute in values\(3.6\times (3)+4.5\times (7) = 10.8+31.5=42.3\)work out (4.8x10 cubed) divided by (1.2x10^-2). give your answer in standard form
Answers
Answer:
4 x 10^5
Step-by-step explanation:
To divide (4.8x10^3) by (1.2x10^-2), we need to divide 4.8 by 1.2, and then multiply the result by 10^3 / 10^-2.
4.8 divided by 1.2 is 4.
10^3 / 10^-2 can be simplified as 10^3 * 10^2 = 10^(3+2) = 10^5.
So, the expression can be written as:
(4.8x10^3) / (1.2x10^-2) = (4 / 1.2) x 10^5
= 4 x 10^5
The standard form of this expression is 4 x 10^5.
A train traveled 10 miles in 6 minutes.
At this rate, how far will it travel in 20
minutes?
Answers
Hey there! I'm happy to help!
First, let's see how many times 6 minutes fits into 20 minutes.
20/6=3 1/3
So, we are traveling 10 miles 3 1/3 times!
10×3 1/3=33 1/3
This train will travel 33 1/3 miles in 20 minutes.
Have a wonderful day! :D
Suppose a Realtor is interested in comparing the asking prices of midrange homes in Peoria, Illinois, and Evansville, Indiana. The Realtor conducts a small telephone survey in the two cities, asking the prices of midrange homes. A random sample of 21 listings in Peoria resulted in a sample average price of $116,900, with a standard deviation of $2,300. A random sample of 26 listings in Evansville resulted in a sample average price of $114,000, with a standard deviation of $1,750. The Realtor assumes prices of midrange homes are normally distributed and the variance in prices in the two cities is about the same. The researcher wishes to test whether there is any difference in the mean prices of midrange homes of the two cities for alpha = .01. The appropriate decision for this problem is to?
Answers
The appropriate decision for this problem would depend on the calculated test statistic and its comparison to the critical value from the t-distribution table with a significance level of 0.01.
To determine the appropriate decision for this problem, the researcher needs to perform a hypothesis test. The null hypothesis (H0) would state that there is no difference in the mean prices of midrange homes between the two cities, while the alternative hypothesis (Ha) would state that there is a difference.
Since the sample sizes are relatively large (21 and 26), and the data is assumed to be normally distributed with similar variances, a two-sample t-test would be appropriate for comparing the means. The researcher can calculate the test statistic by using the formula:
\(t = (x1 - x2) / \sqrt{((s1^2 / n1) + (s2^2 / n2))}\)
Where x1 and x2 are the sample means, s1 and s2 are the sample standard deviations, and n1 and n2 are the sample sizes.
With the calculated test statistic, the researcher can compare it to the critical value from the t-distribution table with (n1 + n2 - 2) degrees of freedom, and a significance level of 0.01. If the test statistic falls within the critical region (i.e., it exceeds the critical value), the researcher can reject the null hypothesis and conclude that there is a significant difference in mean prices between the two cities. Otherwise, if the test statistic does not exceed the critical value, the researcher fails to reject the null hypothesis and concludes that there is not enough evidence to suggest a difference in mean prices.
In this case, the appropriate decision would depend on the calculated test statistic and its comparison to the critical value.
Learn more about variances here: https://brainly.com/question/16902796
#SJ11
12(Multiple Choice Worth 5 points)
(H2.03 MC)
Which of the following is NOT a key feature of the function h(x)?
(x - 5)²
-log₁ x +6
O The domain of h(x) is [0.).
O The x-intercept of h(x) is (5, 0)
h(x) =
0≤x≤4
X>4
O The y-intercept of h(x) is (0, 25).
O The end behavior of h(x) is as x→∞h(x)→∞

Answers
The feature NOT associated with the function h(x) is that the domain of h(x) is [0.).
The function h(x) is defined as (x - 5)² - log₁ x + 6.
Let's analyze each given option to determine which one is NOT a key feature of h(x).
Option 1 states that the domain of h(x) is [0, ∞).
However, the function h(x) contains a logarithm term, which is only defined for positive values of x.
Therefore, the domain of h(x) is actually (0, ∞).
This option is not a key feature of h(x).
Option 2 states that the x-intercept of h(x) is (5, 0).
To find the x-intercept, we set h(x) = 0 and solve for x. In this case, we have (x - 5)² - log₁ x + 6 = 0.
However, since the logarithm term is always positive, it can never equal zero.
Therefore, the function h(x) does not have an x-intercept at (5, 0).
This option is a key feature of h(x).
Option 3 states that the y-intercept of h(x) is (0, 25).
To find the y-intercept, we set x = 0 and evaluate h(x). Plugging in x = 0, we get (0 - 5)² - log₁ 0 + 6.
However, the logarithm of 0 is undefined, so the y-intercept of h(x) is not (0, 25).
This option is not a key feature of h(x).
Option 4 states that the end behavior of h(x) is as x approaches infinity, h(x) approaches infinity.
This is true because as x becomes larger, the square term (x - 5)² dominates, causing h(x) to approach positive infinity.
This option is a key feature of h(x).
In conclusion, the key feature of h(x) that is NOT mentioned in the given options is that the domain of h(x) is (0, ∞).
Therefore, the correct answer is:
O The domain of h(x) is (0, ∞).
For similar question on domain.
https://brainly.com/question/2264373
#SPJ8
Point QQ is located at (3,-1)(3,−1) on the coordinate plane. Point QQ is reflected over the yy-axis to create point Q'Q ′ . What ordered pair describes the location of Q'?Q ′ ?
Answers
The ordered pair that describes the location of Q' is (-3, -1)
How to determine the ordered pair that describes the location of Q?From the question, we have the following parameters that can be used in our computation:
Point Q = (3, -1)
This point can be represented as
(x, y) = (3, -1)
Also, from the question, we have the transformation to be:
Point Q is reflected over the y-axis
Mathematically, this can be expressed as
(x, y) = (-x, y)
So, we have the following representation
Point Q' = (-3, -1)
Hence, the image is (-3, -1)
Read more about transformation at
brainly.com/question/27224272
#SPJ1
Select the correct answer.
Solve the following compound inequality.
5x+75 -3 or 3x-4 > 11

Answers
Answer:
5x+7<_-3
5x<_-7-3=>
5x<_-10=>
x<_-10-5=>
x<_-15.
3x-4>_11
3x>_11+4=>
3x>_15=>
x>_15-3=>
x>_12.
How much money do I need now if I am going to recieve $5000 every 6 months (starting in 6 months) for 10 years if the interest rates are 4%/a compounded semi-annually?
Answers
By using the compound interest model, the initial deposit required to receive $ 5 000 every 6 months is $ 125 000.
How many money should be deposited in the beginning to receive a certain amount periodically
In this problem we must apply the compound interest model, which represent a periodic accumulation of interest according to the following formula:
C' = C · (1 + r/100)ˣ (1)
Where:
C - Initial depositr - Interest rateC' - Resulting moneyx - Period indexIf we know that x = 1, r = 4, C = x and C' = x + 5 000, then the initial deposit is:
x + 5 000 = x · (1 + 4/100)
x + 5 000 = 1.04 · x
0.04 · x = 5 000
x = 125 000
By using the compound interest model, the initial deposit required to receive $ 5 000 every 6 months is $ 125 000.
To learn more on compound interest: https://brainly.com/question/14295570
#SPJ1
Which table of values represents exponential decay?

Answers
The table of values that represents exponential decay is (c)
How to determine the table of values represents exponential decay?From the question, we have the following parameters that can be used in our computation:
The table of values
An exponential function is represented as
y = abˣ
Where
Rate = b
When the rate is less than 1, then the table represents a decay
i.e when y reduces as x increases
The table that has the above features is the table (c)
Read more about exponential function at
brainly.com/question/2456547
#SPJ1
Kathy saves $1 on the first day, $2 on the second day, $3 on the third day and so on,
saving an extra $1 on each subsequent day. On which day will she have $300 or more in total?
Answers
Answer:
Day 24 will be the day she'll reach $300
Step-by-step explanation:
Answer20th
Step-by-step explanation:
Write 0.000673 in scientific notation
Answers
Answer:
6.17
Step-by-step explanation:
Answer:
6.73 × 10-^4
Step-by-step explanation:
Angle formed by two parallel lines cut by a third line. These angles are in the same position and have the same angle measure
What is it?
Answers
Answer:
Corresponding angles
Step-by-step explanation:
The name of these angels lying in the same position are called corresponding angle.
These angles are equal. When we talk of parallel lines, they are sets of lines that travel in the same direction but never meet. The third line that cuts through the two sets of parallel lines is referred to as the transversal line.
So the positions of these angles on each of the set of the parallel lines are equal in each of the cases and they are equal and are referred to as being corresponding to each other
3 5 5 15 17 20 what is the median
Answers
Answer:
Step-by-step explanation:
So find the middle number or middle two
Then if it’s one number it’s that number
If it’s two add them up and divide
In this case it’s 2:5 and 15
5+15=20
20/2=10
So the median is 10
Answer:
3
Step-by-step explanation:
Help !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
______
\( \: \)
\( \tt5 - 6x = 8x + 17\)
\( \longmapsto \tt \: x = \frac{5 - 17}{ - 6 + 8} \)
\( \longmapsto \tt \: x = \frac{ - 12}{8 - 6} \)
\( \longmapsto \tt \: x = \frac{ - 12}{ 2} \)
\( \longmapsto \tt \: x = \boxed{ \blue{ - 6}}\)
Hi purple (I think that was your name) please hopefully you see this I was messing around with this app and I logged out I was logged in with my old school email so now it doesn’t work so I had to make this acc it’s my school new school email please send me the pic of the carnival hw again please.

Answers
Answer:
I'm sorry but I don't know how to do function notation. I'm so sorry that I couldn't help you with this.
Ashwin wrote a plan for a proof. What will help complete his plan?

Answers
Answer:
Corresponding angles of parallel lines cut by a transversal are congruent.